考虑模型不确定和关节电机动态的柔性机械手滑模控制

王春峰

(南京信息职业技术学院智能制造学院，江苏南京 210023)

0 前言

柔性机械手以其负载/质量比大、结构轻巧、效率高等优势，已逐渐取代传统的刚性机械手在航空航天、医疗和工业等领域得到广泛应用。然而，由于其结构柔性的存在，柔性机械手的鲁棒控制一直是控制和应用工程领域的难点之一[1-3]。

柔性机械手建模方法主要有牛顿-欧拉法、拉格朗日法和虚位移法等，最常见的模型有解耦模型[4]、偏微分方程组模型[5]和基于模态假设法的模型。由于模态假设法模型将每个杆视为欧拉-伯努利杆，模型包含分布参数，更接近柔性机械手的真实情况，因此应用最广泛，如文献[6-8]中都用到了模态假设法模型。柔性机械手包含柔性单元，属于典型的分布参数系统，必须用无穷维分布参数模型来描述，然而，为降低模型复杂性，通常柔性模态只截取到1阶。特别地，关节电机安装在机械臂上，通常辅助以谐波减速器、制动器、磁编码器及控制器等，进而通过一个或多个关节电机的联动完成机械手的运动控制[9]。因此，电机动态性的影响不可忽略，但现有建模过程中却常忽略，使得柔性机械手建模精度不高，严重制约了其模型分析与控制精度。

在柔性机械手的控制方面，其末端控制面临的难点之一为转矩输入与位移输出间的传递函数为非最小相位，难以直接针对末端期望位移进行控制器设计。为此，研究人员针对其非最小相位的解耦问题进行了相关研究。文献[10]中在被控系统平衡点处利用输出重定义的方式，将它转变为易于控制的最小相位系统。文献[9]和文献[10]中根据不同时间尺度下的关节电机转角和柔性模态，分别采用奇异摄动方法、输出重定义法将系统分解为快、慢2个子系统。对比以上2种常用解耦方法，输出重定义法应用更广泛、简单且控制器设计灵活。

此外，在应用控制方法方面，对比PI控制[12]、状态反馈控制[13]和模糊控制[14]等，滑模(Sliding Mode Control, SMC)控制[15]以其强鲁棒性、对控制对象模型精度要求不高和易于实现等优点，在柔性机械手控制方法中广泛应用，有效缓解了柔性机械手建模精度的约束。但目前SMC多以传统线性滑模控制、非奇异终端滑模控制[16]及与模糊控制、神经网络等智能控制法相结合[17]的应用为主，且多以额定工况下的柔性机械手控制为主。然而，在对运动精度要求较高的场合中，由于关节电机的动态性能和实际模型中参数的不确定性，SMC控制性能往往不理想。现有控制方法多以稳定性作为控制目标，且无法定量给出其末端位移偏差的准确值。

基于以上研究背景，本文作者以双臂柔性机械手为例，考虑模型参数不确定和关节电机动态，建立一种柔性机械手与关节电机的联合模型，在此基础上，重新定义其输出以解决其最小相位问题。针对分解后的重定义子系统，借鉴文献[18]中的终端滑模的有限时间收敛特性，提出一种改进的非线性滑模控制方法，同时实现对输出重定义系统状态和关节电机动态的鲁棒控制，提高其动态响应时间。针对分解后的柔性模态，利用李雅普诺夫稳定性理论保证它在平衡点邻域的局部收敛性，并推导出双机械手末端位移的误差范围。

1 系统描述与建模

1.1 柔性机械手-关节电机联合建模

针对双臂柔性机械手，本文作者采用文献[18]中的模型。不同于目前柔性模态仅取截断后1阶的做法，该模型每个臂柔性模态均取2阶，因此建模精度更高。考虑模型参数不确定性，双臂柔性机械手系统描述如式(1)所示：

(1)

其中:θ=[θ1θ2]T∈R2为电机转角;q=[q1

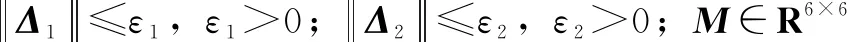
其中：Mr∈R2×2;Mrf∈R4×2;Mf∈R4×4。矩阵M的逆矩阵可表示为

其中:N11∈R2×2;N12∈R2×4;N21∈R4×2;N22∈R4×4。

本文作者着重考虑关节电机的动态。相比于异步电机、步进电机等，直流电机以其结构简单、调速范围大、易于实现线性和快速启停控制等优点在机械手中广泛应用[20]。为此，本文作者采用直流电机充当柔性手的关节驱动电机，其动态特性可表示为

(2)

式中：L=diag[L1L2]、R=diag[R1R2]、Ke=diag[ke1ke2]，分别表示2个柔性臂上电机的电感、电阻和反电势常数阵；KT为电机的电流-转矩正定常数阵；u=[u1,u2]T∈R2为关节电机的输出转矩;Te=[Te1,Te2]T∈R2为关节电机的机械转矩，且有u=Te+τ。

(3)

其中:

文中控制目标：控制双臂柔性机械手的末端位移从非零初始状态yi(0)≠0到零，其计算公式如式(4)所示：

(4)

式中:yi(0)、Li和φij分别为第i个柔性机械手的初始位移、臂长和第j个柔性模态。

柔性机械手系统的输入维数小于输出维数，属于非最小相位系统，难以直接设计控制器。因此，借鉴文献[19]中的输出重定义方法进行模型变换。

1.2 模型变换

根据式(4)，为克服柔性机械手末端控制的最小相位问题，重新定义输出变量z∈R2为电机转角θ和柔性模态q的线性组合为

z=λ0θ+λ1q

(5)

式(5)中并没有把关节电机模型(2)的变量I考虑到重定义输出变量z中，因为关节电机只是通过电流I为柔性机械手提供驱动转矩，而式(4)表示的末端位移的控制仍然通过控制关节转角θ和柔性模态q实现。

将式(5)中的z进行两次求导，可得关节电机的输出转矩u，并将u代入式(3)，有：

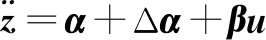
(6)

其中:

(7a)

Δα=(λ0N11+λ1N21-N11Te)Δ1+(λ0N12+

λ1N22-N21Te)Δ2

(7b)

β=λ0N11+λ1N21

(7c)

(8)

根据文献[19]中输出重定义方法，式(8)可视为输入、输出子系统，而其余4维柔性模态构成内部子系统，由式(3)可直接得到：

Kq-Δ2)+N21u

(9)

若针对如式(9)所示的重定义输出系统设计控制律u使其状态z1=z2=z3=0有限时间收敛，则式(6)成立，进而推出:

u=-β-1(α+Δα)

(10)

将式(10)代入式(9)，根据文献[10]中零动态的定义，内部子系统化为零动态子系统:

(11)

综合以上模型变换，可见如式(3)所示的柔性机械手-关节电机联合模型可最终分解为如式(8)所示的重定义子系统和如式(11)所示的零动态子系统。

2 非线性滑模控制器设计

针对重定义输出系统，由于包括3个系统状态z1、z2和z3且为实现有限时间收敛，借鉴文献[18]中终端滑模的有限时间收敛特性设计一种改进的非线性滑模面，其表达式为

(12)

式中：s∈R2；设计参数为c1、c2，并且c1=diag[c11

c12]、c2=diag[c21c22]，cii>0,i=1, 2。

式(8)中包含未知的不确定项Δα，在设计相应滑模控制器时需要知道其上边界范围，则有：

(13)

其中:ε3>0。

基于滑模等效控制原理[2]，设计滑模控制律u由等效控制项ueq和切换项un组成，即:

u=ueq+un

(14)

令式(12)中的s的一阶导为0，可以计算得到等效控制项ueq，旨在维持系统在滑模面稳定。ueq表达式为

ueq=Rz3+Kez2+Te-

(15)

而切换项un的作用是通过切换开关使得系统趋近于设计的滑模面，其优点为具有高度抗干扰性。

(16)

将式(15)代入式(16)，则有:

(17)

可见，若设计切换项un为

(18)

其中，η>0则可使得式(17)变为

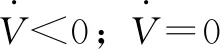
结合以上分析，可证明所设计的控制律u的正确性及系统状态的有限时间收敛性。

3 稳定性分析

由式(11)可知，零动态系统的稳定性能决定整个柔性机械手系统的稳定性能，且由于不确定性Δ1、Δ2的存在，可知在x=0时具有局部稳定性，假设其稳定区域为Ω。为此，在其局部稳定区域可对矩阵N和ff进行线性化，即有：

(19)

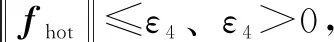
将式(19)代入式(11)有：

(20)

其中：

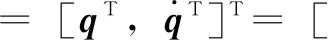
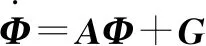
(21)

其中：

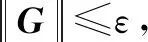
(22)

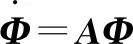
(23)

由式(23)可推导出柔性模态q的收敛范围为

(24)

结合式(14)(15)和(18)所示控制律的作用，由式(5)重定义输出变量z=λ0θ+λ1q=0成立，因此可推导出电机转角θ的收敛范围：

(25)

最后根据柔性机械手末端位移的计算公式，考虑关节电机与参数不确定情况下，得到双臂柔性机械手末端位移误差范围为

(26)

4 数值仿真

为验证所提控制方法的有效性，从重定义参数λ0和λ1、模型参数不确定和关节电机动态三方面分析其对柔性机械手稳定性和控制性能的影响。表1给出了双臂柔性机械手模型参数。

表1 双臂柔性机械手模型参数

(1)重定义参数对稳定性能的影响

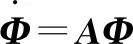
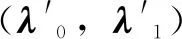
图1 重定义系数对零动态系统状态的影响

(2)模型参数Δ1和Δ2对系统性能的影响

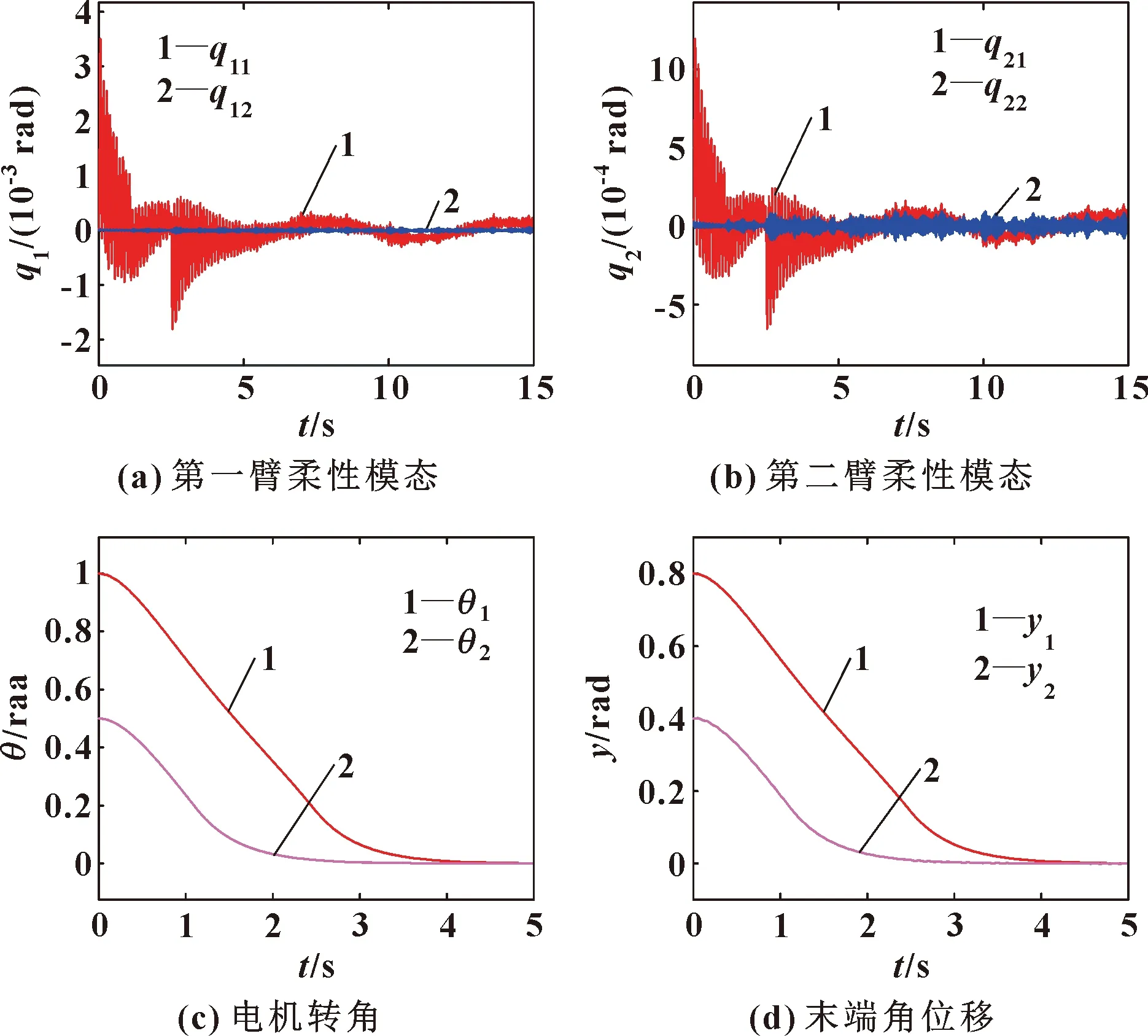
图2 存在模型不确性的柔性机械手仿真结果

(3)关节电机动态对系统性能的影响

不考虑模型参数的不确定Δ1和Δ2的影响，式(2)中关节电机参数如表2所示。在基于文献[19]中忽略关节电机的影响建模和控制器设计的基础上，增加关节电机动态的控制，选择参数c2=diag[1.2,1.2]，对比仿真结果如图3所示，其中，有关节电机采用如式(12)所示的非线性滑模，没有关节电机采用文献[19]中的标准终端滑模。

表2 直流电机参数

由图3(a)(b)可见：文献[19]中的标准终端滑模和文中设计的非线性滑模变量均可实现有限时间收敛，但不考虑关节电机动态的情况下收敛时间延长，意味着柔性机械手-关节电机联合控制会使系统响应速度加快。由图3(c)(d)可知：若考虑关节电机动态，其对应输出的关节驱动转矩作用也会变大，即需要额外的驱动扭矩用于关节控制。由图3(e)(f)可知：关节电机动态的联合控制具有加快系统响应速度的作用。利用LMI工具箱和式(25)—(26)可算出存在关节电机动态时2个柔性机械手的末端误差分别为1.699×10-4rad 和8.71×10-4，因此在建模和控制器设计时不应忽略关节电机动态。

图3 考虑/不考虑关节电机特性的柔性机械手仿真结果

5 结论

本文作者针对双臂柔性机械手系统，着重研究了关节电机与模型不确定对末端位移误差的影响。建立了双臂柔性机械手-关节电机的联合数学模型，并利用重定义方法解决其非最小相位问题。针对分解后的重定义子系统，提出一种改进的非线性滑模控制方法，实现了重定义输出变量和关节电机动态的鲁棒控制。针对零动态子系统，利用Lyapunov稳定性定理推导出重定义参数与零动态子系统稳定性、末端位移误差的关系。仿真结果证明了模型不确定性和关节电机的影响不可忽略，所提方法具有参考价值。