基于动态贝叶斯网络的多状态系统可靠性分析

齐金平，李少雄，周亚辉 ，王康

(1.兰州交通大学机电技术研究所，甘肃兰州 730070；2.甘肃省物流及运输装备信息化工程技术研究中心，甘肃兰州 730070；3.甘肃省物流与运输装备行业技术中心，甘肃兰州 730070)

0 前言

故障树分析法(Fault Tree Analysis,FTA)是可靠性研究方法之一，已使用普遍，但其故障概率精确已知、逻辑门之间必须联系明确等条件限制了它在可靠性分析以及故障诊断中的应用，T-S模糊故障树既考虑到故障程度对系统的影响，也解决了事件之间的不确定性问题，但不能逆向推理。贝叶斯网络(Bayesian Network，BN)的优势在处理复杂系统可靠性问题时进一步凸显，不仅广受青睐，还得到了扩展，出现了离散、模糊、动态等贝叶斯网络，相对于现存可靠性分析方法，BN层次清晰分明，推理关系明确，辅助软件发展成熟，但建模相对困难。将两种方法综合求解，可将其建模推理优势充分利用。

李兴运、齐金平将T-S模糊故障树转化为BN解决了受电弓系统的多态性问题；任宇超等以联接树算法为基础，对地铁车门建立故障贝叶斯网络,对其进行可靠性分析；张友鹏、解绍锋等对不同的系统构建以故障树为基础的贝叶斯网络，从而求解相关指标并寻出系统易故障部件。黄洪钟等对太阳翼进行了动态故障树分析(Dynamic Fault Tree Analysis，DFTA);房丙午等提出基于动态贝叶斯网络(Dynamic Bayesian Network，DBN)的复杂系统定量分析；郭济鸣等以制动系统为例，构建DBN进行可靠性分析。

以上方法都是单纯的基于动态故障树或离散BN的动态分析，无法刻画出任意形式的失效行为，且难以反映可靠度与时间的函数关系。本文作者将基于冲激函数约束连续时间T-S动态故障树，映射新型动态贝叶斯网络，在GeNIe2.0软件中搭建贝叶斯网络模型，导出后验概率，再计算合成动静态模块重要度，发挥两者对复杂系统的建模与推理优势，并为寻找系统薄弱环节提供依据，最后借助相关软件仿真出系统的可靠度-时间变化曲线。

1 T-S模糊动态故障树

T-S模糊动态故障树区别于T-S模糊故障树，它是基于动态门的时序逻辑关系构建，每条规则(=1,2,…,)为一个下级事件的故障时序。假设与分别表示(=1,2,…,)(下级事件)与(上级事件)故障时间和冲击点时刻，=即与故障时间一致，则冲击函数约束与的故障时间表达式(1)所示：

(1)

其中:表示事件，冲击点的时刻为，当=，即(-)=∞时，故障后立刻故障。

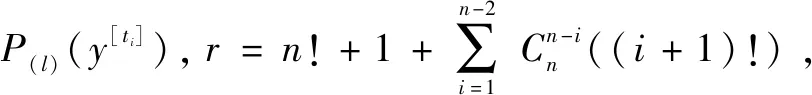
表1 T-S动态门的描述规则

2 新型模糊动态贝叶斯网络

在静态模糊BN中融入时间序列得到新型模糊DBN，基于第1节T-S模糊DFTA表述模糊DBN步骤如下：

(1)T-S模糊动态故障树映射为模糊DBN，如图1所示；

图1 T-S模糊DFTA到模糊DBN映射图

(2)动态门及规则对应表述条件概率表，具体如下：

若表示系统任务时间，以间隔=将总任务时间分为[0,),[,2),…,[(-1),),[,+∞)共段，记为时间段1,2,…,+1，假如父节点在时间段(=1,2,…,,+1)失效，子节点在时间段失效状态为[]，则映射后的条件概率如表2所示。

表2 DBN条件概率

2.1 叶节点失效概率

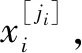
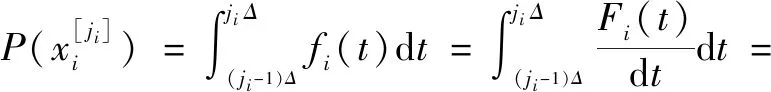
[exp()-1]exp(-)

(2)

式中:()为根节点的概率密度函数;()为根节点的不可靠度;为的失效率。

(3)

2.2 根节点后验概率及重要度

根据贝叶斯网络反向推理特点，若已知时间段的失效概率，可得根节点的后验概率

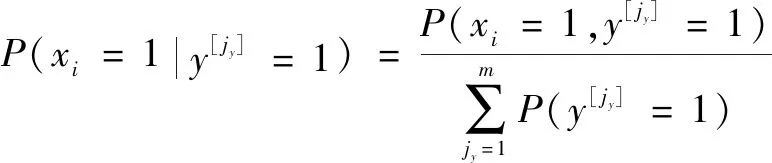
(4)

根据上式，可得根节点在任务时间失效的后验概率为

(5)

复杂系统中部件的重要性呈现非均等特性，重要度是可靠性分析中的一个重要指标，系统随着根节点失效状态的概率变化而变化的程度即为概率重要度，当叶节点在时间段内失效时根节点的概率重要度为

(6)

根节点在时间段内的概率重要度为

()=()·()

(7)

式中:()为每个底事件相对于系统的重要度;()为底事件对于子树的重要度。

3 多状态系统动态性可靠性分析

3.1 动车组空气供给系统

以动车组空气供给系统为例，对其可靠性分析。系统工作时，空压机产生的压缩空气通过列车上的总风管传输，途经控制风管，至控制、制动风缸，如图2所示。

图2 空气供给系统简图

3.2 系统建模及可靠性分析

对某动车所动车组运行的历史故障数据进行归类、整理统计，综合专家调查法与模糊数学知识分析处理，得到故障率较高的部件及其故障率，以其部件为底事件，以空气供给系统为顶事件建立T-S模糊DFTA如图3所示，事件名称及模糊故障率如表3所示。

表3 事件代号及故障率

根据图3所示的T-S模糊DFTA可得图4所示的DBN图。

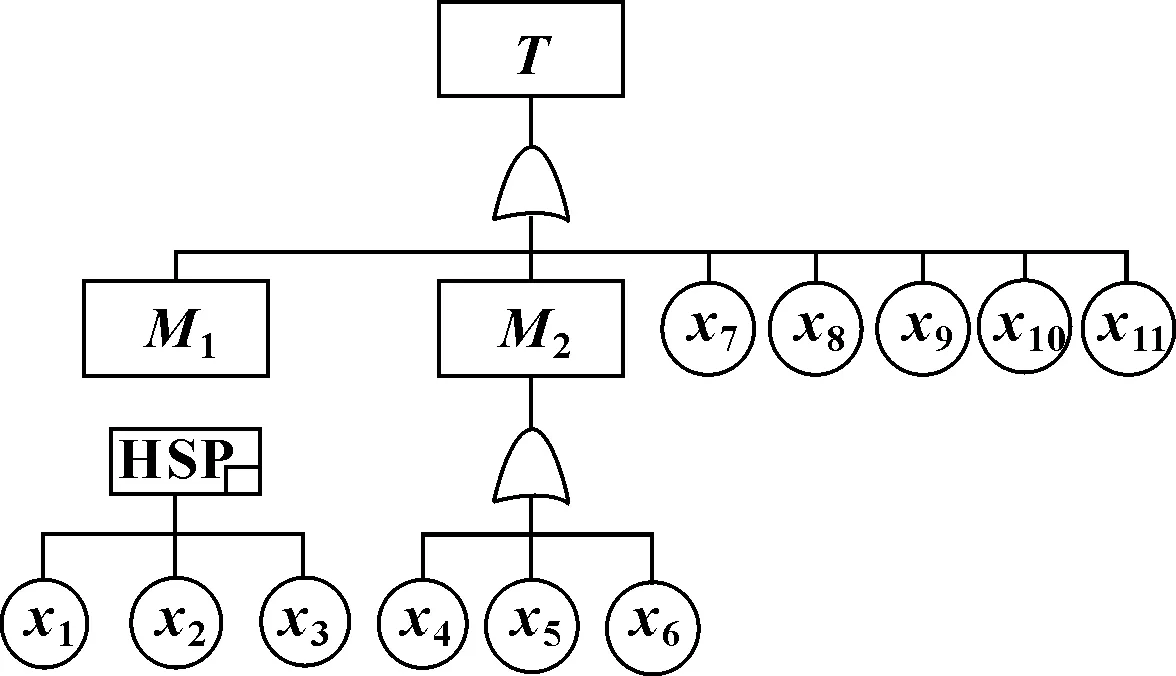
图3 空气供给系统故障树

图4 空气供给系统DBN图

假设任务时间为15 000 h，取=3 000 h，根据上述新型贝叶斯网络方法，在GeNIe2.0软件中绘制贝叶斯网络，根据表2，得叶节点故障概率如表4所示，用模型导出后验概率，根据式(6)(7)计算根节点相对于叶节点的重要度，数值如图5所示。

表4 叶节点故障概率

图5 系统重要度与后验概率分布

由图5可知，安全阀()与单向阀()为系统的薄弱环节，若失效对系统的可靠度影响较大，应加大检查检修频次，其余部件可参考图示结果合理安排设备维护频次。

根据文献[14-15]，假设～均服从指数分布，在MATLAB软件中编程仿真得系统可靠度变化曲线如图6所示。可知:系统可靠度时间曲线纵向间距与时间保持正相关，这是因为部件随着使用时间的增加，其可靠度的不确定性随之变大。

图6 系统可靠度变化曲线

4 结论

(1)新型动态贝叶斯网络的提出，既发挥了连续时间T-S模糊动态故障树的动静态描述能力，又发挥了贝叶斯网络的双向推理建模与可描述动态优势。基于冲激函数约束的连续时间T-S动态故障树映射贝叶斯网络，也解决了直接建立复杂贝叶斯模型的难题。

(2)以动车组空气供给系统为例对其可靠性分析，原始的贝叶斯网络模型只能分析故障的单一状态，通过考虑故障的多态性，本文作者结合模糊数学理论建立模糊贝叶斯网络模型，能够同时分析故障的多态性和动态性。

(3)计算叶节点的故障概率，并通过仿真分析，得到动车组空气供给系统随时间变化时根节点的后验概率以及重要度，并于软件中仿真出可靠度-时间的变化曲线。