基于电磁激振的风电叶片双向疲劳加载控制算法研究
2022-10-13范治达张磊安黄雪梅叶凯
范治达,张磊安,黄雪梅,叶凯
(山东理工大学机械工程学院,山东淄博 255000)
0 前言
进入21世纪后,随着全球人口数量迅速增长以及人们对现代化需求的不断增加,能源的消耗量日渐增加,发展可再生能源成为必然选择。风能在全球范围内分布广泛、储量巨大,是一种可无限利用、对环境友好的清洁能源。风力发电机组利用叶片将气流的机械能最终转为电能,因此风电叶片的性能能否达到要求至关重要。由于风力机叶片长期工作在载荷不断变化的环境中,近1/2的风力机因为叶片受到疲劳损伤而出现故障。由于叶片材质、结构、工艺以及工作环境复杂,对风电叶片疲劳寿命的理论计算必须通过风电叶片全尺寸疲劳测试的验证。国内外针对叶片疲劳加载的方法已经有了一定的研究。目前国外一般采用强制位移型疲劳加载方法对叶片进行疲劳测试,而摆锤共振型叶片疲劳加载方法在国内得到了广泛使用。虽然这两种方法被普遍应用,但在叶片疲劳加载中仍存在以下问题:叶片的疲劳分析数据与实际情况误差较大,输出的载荷谱与预设的载荷谱有差距,不能较为准确地施加符合实际情况的载荷。而基于液压作动器的疲劳加载系统,硬件复杂,需要配置液压站,试验成本高、周期长。在叶片疲劳加载控制算法方面,国内外学者在风电叶片疲劳加载控制领域做了相应研究。于祥勇等研究了一种基于RLS算法的实际振幅与目标振幅的追踪控制策略。廖高华等提出了基于虚拟主令偏差耦合的同步控制策略。陶黎明等提出了基于自抗扰控制算法的交叉耦合控制策略。TOFT等提出了一套风电叶片疲劳试验线性控制策略。孔晓佳等提出一种基于变增益交叉耦合控制器的速度并行控制算法。上述研究成果虽然在各自领域取得了良好的控制效果,但不适用于电磁力驱动的双轴疲劳加载的控制系统。因此,本文作者从提高疲劳测试精度和安装、操作便捷的角度出发,提出一种基于电磁力驱动的风电叶片疲劳加载新方法。采用一种具有可调增益的模型参考自适应控制算法,并设计自适应律,仿真结果表明改进后的算法鲁棒性好,削弱了噪声干扰;最后通过搭建试验台验证了该算法的有效性。
1 电磁力驱动的风电叶片双向疲劳加载方案
在叶片双向电磁疲劳加载系统中,作用在叶片上的激振力是由电磁激振器的脉冲力提供的,当电磁激振器的激振频率与叶片的低阶固有频率相近时,叶片将产生共振并达到最大振幅且振动频率与电磁激振频率相同。电磁激振器包括铁芯、线圈、外壳。确定电磁激振器后,电磁力的大小与铁芯进入线圈的长度有关,当铁芯逐渐进入线圈时,电磁力逐渐增大,当到达线圈长度的40%~80%时,电磁力达到且稳定在最大值;铁芯超过线圈长度80%后,电磁力开始减小,达到100%后电磁力减小到0。为补充振动过程中叶片损耗的能量,铁芯在每个周期对叶片补充两次能量。铁芯运动规律及振动位置如图1所示。
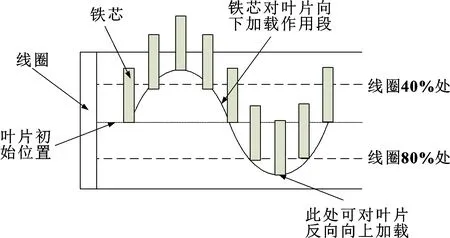
图1 电磁铁芯运动规律及振动位置
当叶片振动进入稳定状态后,在每个周期中,系统阻尼损耗的能量与电磁激振器提供的能量相互平衡,即=,其中:
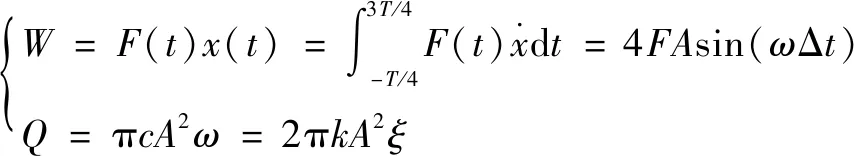
(1)
式中:为频率;为振幅;为电磁激振力()在每个周期做的功;为振动周期;为阻尼比;为阻尼;为叶片刚度。根据能量守恒定理,可计算出电磁加载力、铁芯直径的平方和铁芯质量:

(2)
式中:、、、、分别表示电磁铁芯直径、电流、铁芯长度、线圈匝数、铁芯密度。
根据振动原理,在电磁激振作用下,叶片振动过程为受迫振动,因此该系统的振动微分方程可表示为式(3)。其中,下标f表示挥舞方向,下标e表示摆振方向,、分别为摆振及挥舞方向的位移。
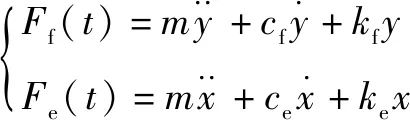
(3)


(4)
2 可调增益的模型参考自适应控制算法
在风电叶片双轴电磁疲劳加载系统中,挥舞方向与摆振方向相互之间存在干扰作用,需采用具有较好抗扰动能力的控制算法。可调增益的模型参考自适应控制算法通过不断地调节可调系统的增益参数,使系统的输出不断逼近模型的输出,从而使误差接近为0并且保证了控制系统的抗扰动能力以及稳定性。该算法主要部分包括参考模型、被控系统以及自适应调节规律。
设被控系统的传递函数为
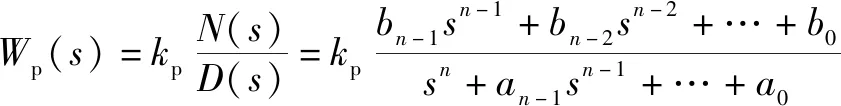
(5)
式中:、、为已知常数,=0,1,…,-1;为随时间缓慢变化的参数。将参考模型设计为

(6)
将控制器设计为如式(7)所示,其中为时间的函数,表示调节规律:
()=
(7)
参考模型和被控模型的系统结构如图2所示。

图2 控制系统结构
为确保控制系统的稳定性,需要求解调节规律。由图2可知=-+,令=-,因此有:

(8)


(9)
可将状态方程表示为

(10)

=

⋮
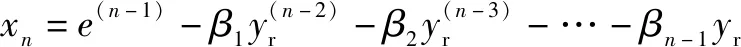
(11)
矩阵、和分别如式(12)、(13)所示:

(12)
=[…]
=[1 0 … 0]
(13)
其中:
=-1
=-2--1
⋮
=--1-1--2-2-…-
(14)
选取如式(15)所示的Lyapunov函数,为对称的正定矩阵,>0。
=+
(15)
由式(15)运算可得:

(16)
令式(15)最右端两项相加为0,即:

(17)
自适应调节规律由式(17)确定,可表示为

(18)
在控制系统中,缓慢时变,可以将其看作定值,由=-可得:
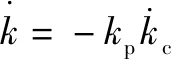
(19)
将式(19)代入式(18),可得自适应调节规律:
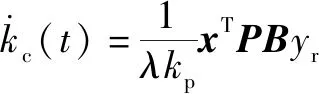
(20)
根据自适应原理,式(20)可转化为
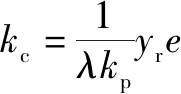
(21)
因此,控制结构如图3所示。

图3 可调增益模型参考自适应控制结构
3 仿真分析
为验证可调增益模型参考自适应算法在电磁激振双轴疲劳加载模型控制系统中的控制效果,在MATLAB中,使用Simulink将该控制策略与PID控制策略通过仿真进行验证以及比较。首先,为验证两种控制策略的跟随效果,根据双轴电磁疲劳加载模型现场试验,在挥舞方向选取幅值为6 cm、频率为2π的sin函数,在摆振方向选取幅值为3 cm、频率为3π的sin函数,普通PID的双向跟随效果及误差分别如图4、图5所示。

图4 普通PID跟随效果 图5 普通PID跟踪误差
由图4、图5可知:由于摆振即挥舞方向的相互干扰,总体跟踪效果很差,在挥舞方向,误差最大达到1.7×10m,偏差为28%;在摆振方向,最大误差为1×10m,偏差为33%,由此可以得出传统PID不能实现电磁加载源与叶片的同步控制。
可调增益的模型参考自适应控制算法仿真效果如图6、图7所示。

图6 可调增益模型参考自适应控制跟随效果 图7 可调增益模型参考自适应控制跟踪误差
由图6、图7可知:在=0.4 s后,跟随过程迅速进入稳定状态,进入稳定状态后挥舞方向最大误差为6×10m,偏差为10%;摆振方向最大误差为2×10m,偏差为7%。采用该算法后,幅值衰减问题已得到改善,初步达到了期望的跟踪效果。
由此可以得出,可调增益模型参考自适应控制算法相较于PID算法有更好的稳定性且收敛速度更快、跟踪精度更好。考虑到仿真中算法的实现有一定的理想性,需要通过现场试验进一步验证。
4 试验以及分析
将2 m长的叶片模型根部固定在电磁疲劳加载试验台上,在安装在适当位置的叶片夹具上连接加载装置。通过上位机软件LabVIEW对试验过程中的位移、力、频率等进行监控并记录数据。电磁加载源参数如表1所示。

表1 电磁加载源参数
在电磁疲劳加载过程中,控制系统采用与仿真相同的参数设置并使电磁激振器的激振频率接近叶片挥舞、摆振两个方向的低阶固有频率,采用可调增益模型参考自适应控制算法进行试验。图8所示为挥舞方向的幅值试验曲线,在0.5 s开始,叶片幅值响应开始跟随,在2 s后达到理想振动状态。图9所示为摆振方向幅值响应曲线,在1 s时开始跟随,在3.5 s后达到理想振动状态。
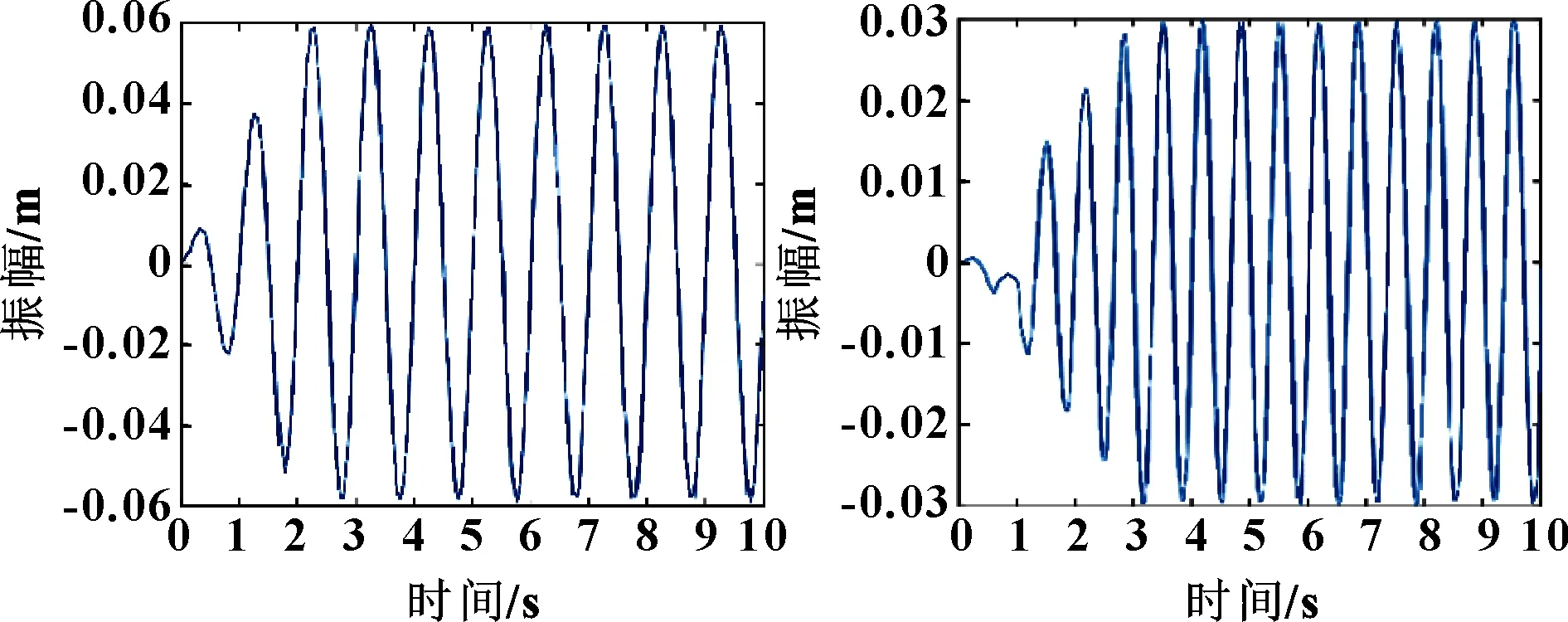
图8 挥舞方向 图9 摆振方向
根据试验结果可知:采用可调增益模型参考自适应算法后,电磁加载装置可以很好地使叶片模型共振并逐步稳定在共振顶峰,叶片模型在挥舞方向及摆振方向的振动幅值分别稳定在0.06、0.03 m,证明了在此试验条件下,该算法对电磁疲劳加载系统的同步控制是可行的,验证了文中算法的有效性。
5 结论
(1)提出了风电叶片双轴电磁疲劳加载方法,对叶片疲劳加载进行了能量分析,对电磁加载过程建立了状态空间方程。
(2)考虑到双轴疲劳加载相互干扰的问题,采用了可调增益模型参考自适应控制算法,将该算法与PID算法在Simulink中进行了仿真及对比。结果表明:在挥舞及摆振方向,相较于传统PID算法,可调增益模型参考自适应控制算法具有跟随效果好、精度更高的优点。
(3)搭建一套风电叶片模型双轴电磁疲劳加载试验平台,在现场试验中对该控制算法进行有效性测试。试验结果表明:叶片挥舞及摆振方向的振幅很快达到稳定状态,并能很好地维持住同步状态,风电叶片双向电磁疲劳加载试验的控制精度得到了提高,采用的算法具有良好的鲁棒性。
