改进EWT降噪与快速谱相关的滚动轴承早期故障诊断

2022-10-13朱朋裴雪武周祖清

机床与液压 2022年18期

朱朋，裴雪武，周祖清

(重庆交通大学机电与车辆工程学院，重庆 400074)

0 前言

滚动轴承作为机械设备的关键零件之一，其健康状态直接影响设备的服役状况，对其早期微弱故障进行诊断具有重要的经济效益。然而，机械设备常常工作在恶劣环境与复杂工况下，传感器采集到的早期微弱故障信号常常淹没在强背景噪声下，增加了故障诊断难度。因此，研究高效故障诊断方法对快速、准确地识别轴承早期故障具有重要意义。

针对滚动轴承故障诊断，常用的方法有小波变换和经验模态分解(Empirical Mode Decomposition，EMD)。小波变换降噪效果受小波基和分解层数的影响较大，缺乏自适应性。经验模态分解没有完备的数学理论、存在端点效应等问题。针对该问题，GILLES提出一种新的实现信号自适应分解的方法——经验小波变换(Empirical Wavelet Transform，EWT)。吕跃刚和何洋洋将EWT与独立分量分析相结合进行联合降噪处理，并对降噪后的信号进行Hilbert解调处理获得故障特征频率，实现故障诊断。但是，EWT频带划分方式受信号噪声影响较大，存在频带划分不合理的问题。针对此问题，李政等人提出基于改进EWT与最大相关峭度卷积的早期故障诊断方法，并取得较好的诊断效果。

杨蕊等人基于对滚动轴承故障振动信号具有循环平稳特性的理解，将循环平稳信号处理相关算法引入到滚动轴承早期微弱故障识别。根据统计理论，信号的二阶统计量不仅可以更好地表征周期脉冲特征，而且在一定程度上抑制了随机噪声。因此，基于二阶统计量的循环谱相关分析是分析循环平稳信号的有力工具。ANTONI等针对传统谱相关技术计算效率低的问题，提出了一种新的基于短时傅里叶变换的快速谱相关(Fast Spectral Correlation，Fast-SC)算法，并在轴承信号中进行了研究。但是，轴承早期微弱故障特征常常被噪声干扰所淹没，如果直接使用Fast-SC对原始信号进行分析，会降低对有效特征信息的识别精度，甚至无法识别。

综上所述，本文作者针对滚动轴承早期微弱故障特征淹没在强背景噪声环境下难以诊断的问题，提出改进经验小波变换降噪法，降低微弱信号中的噪声干扰。对降噪后的信号进行Fast-SC分析，获得快速谱相关谱及其对应的均方增强包络谱。通过均方包络谱的频率特征实现早期故障诊断。

1 基本理论

1.1 EWT分解原理

EWT主要是对频谱进行自适应划分。首先，将振动信号变换到归一化的傅里叶谱[0,π]上，根据信号傅里叶频谱特性进行自适应划分；然后，根据划分的边界建立一个经验小波滤波器组并对待处理信号进行滤波；最后，得到一组固有模态分量。

假设用傅里叶紧支撑将[0,π]分割成个连续部分，如式(1)所示：

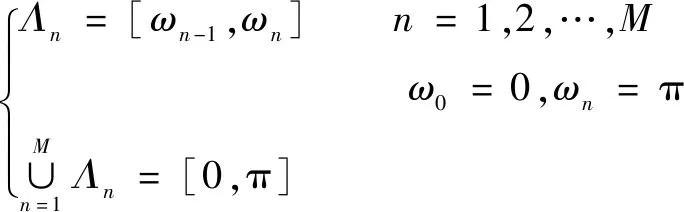
(1)

以为边界，则每一段的傅里叶频谱区间范围为=[-1,],=1,2,…,,第一个边界=0，最后一个边界=π，如图1所示。

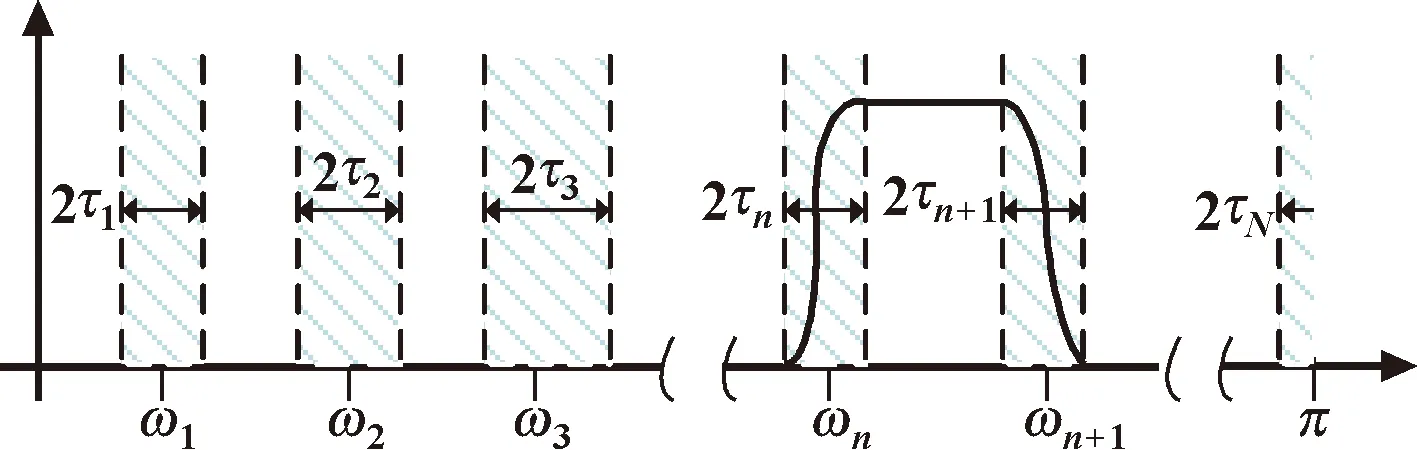
图1 傅里叶分割轴

根据Meyer小波确定经验小波尺度函数式(2)和小波函数式(3)，并构造经验小波滤波器。

(2)

(3)

式中：()在[0,1]内满足阶可导，且可为任意函数；为过程区间参数。和()可表示为

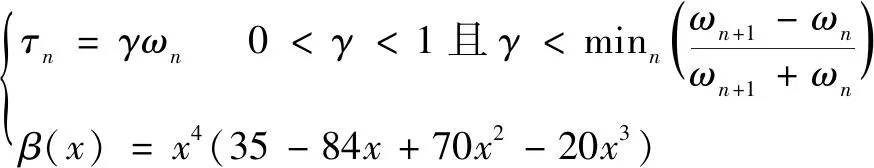
(4)

根据经典小波变换的构造方法构造经验小波变换细节系数和近似系数分别如式(5)和式(6)所示:

(5)

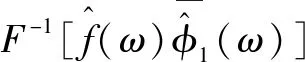
(6)

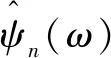
由以上公式得到经验小波滤波固有模态函数，可以由以下形式表示：

(7)

(8)

式中：⊗表示卷积运算，则原始信号的重构公式为

(9)

1.2 循环平稳原理

当滚动轴承发生局部故障时，传感器采集到的振动信号为典型的调制信号，其二阶统计量具有周期性，为二阶循环平稳信号。一个二阶循环平稳信号自相关函数为

(,)={()(-)}

(10)

式中：表示延迟时间；符号*表示共轭运算。

将信号()在周期为的时间内进行采样，自相关函数可以进一步表示为

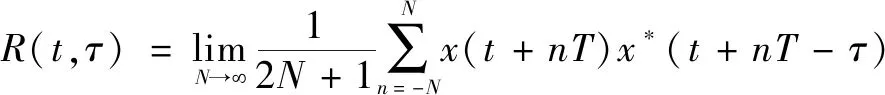
(11)

式中：表示数据点。基于(,)的周期性，式(11)可以进一步展开为傅里叶级数形式：

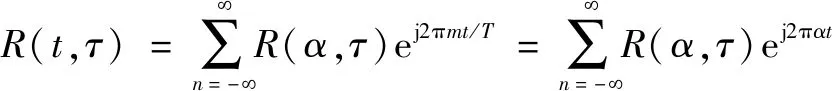
(12)

式中：为循环频率。对(,)进行傅里叶变换，得到如下循环谱：

(13)

1.3 快速谱相关

通过循环谱分析，一维振动信号分析可转化为二维的频率与循环频率的分析。但是，在计算循环谱时，不仅需要进行谱运算，还需要计算信号中不同频率分量之间的谱相关性，耗时较长。针对该问题，ANTONI等提出快速谱相关算法，如下所示：

(1)初始化输入参数

初始化振动信号()及采样频率；选择窗口长度及最大循环频率。

(2)计算振动信号()的离散短时傅里叶变化

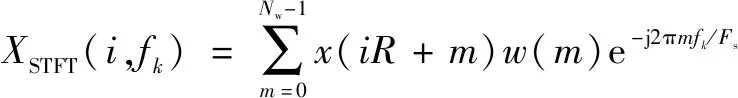
(3)计算频谱相关性

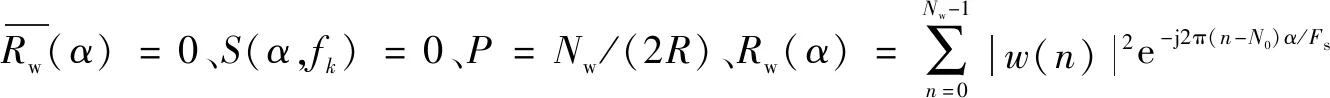
循环计算：

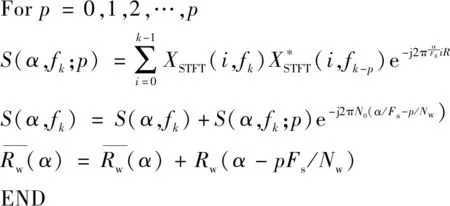
(4)校准幅度

(5)计算频谱相关性

(6)计算增强包络谱(Enhanced Envelope Spectrum，EES)

为进一步突出非零循环分量，提高滚动轴承故障的识别精度，LI等提出了均方增强包络谱(Squared Enhanced Envelope Spectrum，SEES)：

(14)

2 改进EWT降噪与快速谱相关的滚动轴承微弱故障诊断方法

2.1 改进EWT频带划分方式

针对EWT频带划分方式受噪声影响较大、划分不合理的问题，提出迭代极大值包络谱的EWT频带划分方法。算法如下：

(1)将采集到的信号()进行傅里叶变换后得频谱函数()=[()]；

(2)对()中的极大值点进行三次样条插值运算，得包络谱函数()；

(3)()极值点个数对趋势包络谱波形影响较大，因此，需判断函数()的极大值个数是否大于阈值，若大于则进行步骤(4)运算，若小于，对函数()进行极大值三次样条插值运算后得函数()，再次判断极大值个数，若不满足条件再次进行极大值包络处理；

(4) 将最终获得的函数UPP,()作为频谱进行EWT自适应分解，获得频谱划分边界，并以此作为频谱()的划分边界，进行模态分量IMF的提取。

2.2 所提出滚动轴承微弱故障诊断方法

针对滚动轴承早期故障特征微弱，淹没在强噪声工业环境下较难识别的问题，结合EWT降噪及快速谱相关算法，提出一种故障诊断方法，如图2所示。

图2 所提方法诊断流程

3 仿真信号分析

根据单点损伤理论模型叠加高斯噪声，建立外圈故障仿真信号()，令()为含噪信号，则：

(15)

设置幅值常数=1，阻尼=005，固有频率=3 000 Hz，故障频率=130 Hz，故障周期=1，采样频率12 kHz，采样点4 096个，加入的高斯白噪声(SNR)为-12 dB。图3所示为仿真信号时域图。图4所示为仿真信号包络谱图，可发现其3倍外圈故障频率谐波。

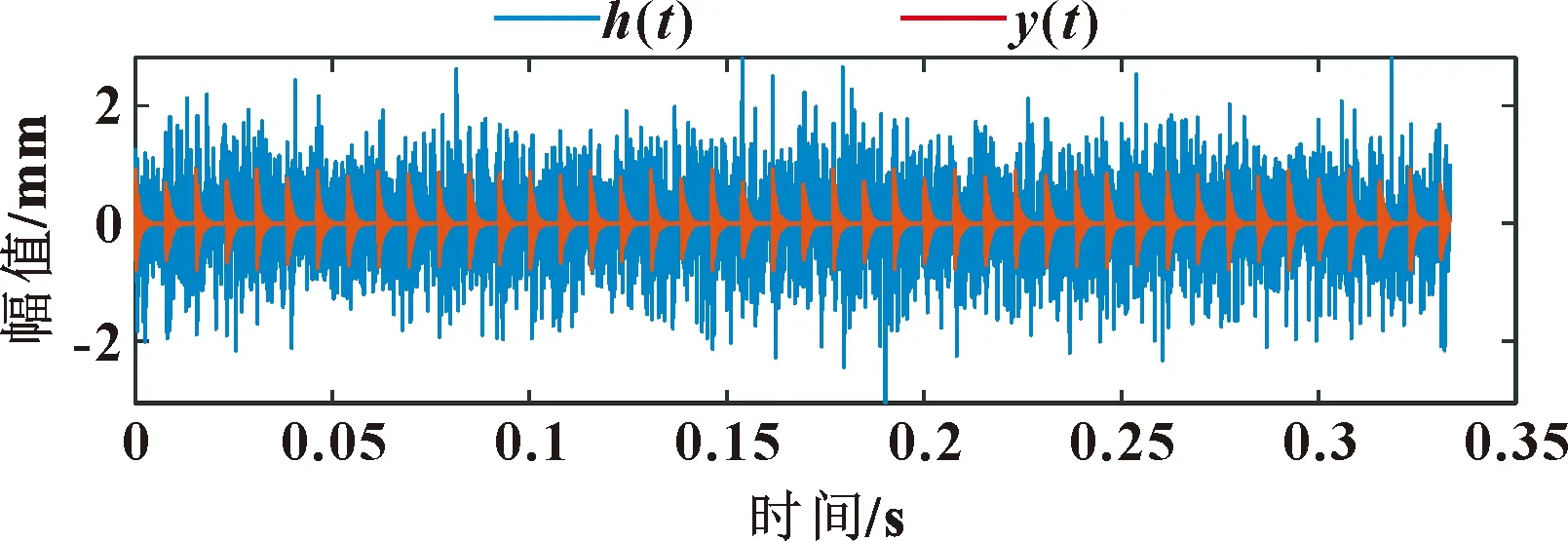
图3 仿真信号时域图

图4 仿真信号包络谱

采用文献[8]提出的快速谱相关分析与增强包络谱对仿真故障信号进行分析，设置窗口长度=2，循环频率=1 000 Hz，所得结果如图5所示。由图5可知，通过对信号快速谱相关分析，增强了故障信号的周期成分，一定程度上抑制了噪声的影响。在增强包络谱中发现1～4倍故障特征频率，但由于强背景噪声的影响，其幅值并不突出，需进行进一步降噪处理。

图5 文献[8]方法分析结果

采用本文作者提出的方法对故障信号进行降噪处理。设置极大值个数为50，最终进行5次连续极大值包络处理，所得频带划分结果如图6所示。其中，图(a)中蓝色的线条表示信号的频谱，其余5种颜色的线条分别表示第1～5次极大值包络处理后获得的结果。由图6可知，极大值包络在前几次过于粗糙，不能有效反映包络频率的趋势，随着包络次数的增加，趋势越来越明显。但包络次数过多会改变频谱的真实趋势，造成频谱划分不合理。

图6 文中所提的EWT频带划分结果

未改进EWT频带划分结果如图7所示。为对比改进的效果，对比图6和图7，可知：文中所提方法能有效地将故障的共振频带划分到同一个模态分量；未改进的EWT频带划分受噪声影响较大，频带划分过于集中，将包含故障特征信息的共振频带划分到几个子带中，影响降噪效果。

图7 未改进的EWT频带划分结果

采用所提方法对仿真信号进行自适应分解的结果如图8所示。分解获得5个模态分量(IMF),各模态分量的峭度如表1所示。

图8 改进的EWT仿真信号分解结果

表1 改进EWT分解效果

由表1可知：IMF4峭度最大，为3.122 5，则它含有较多的故障冲击特征成分，其余分量含有较多的背景噪声，故障特征较弱。因此，选择IMF4进行快速谱相关分析，所得结果如图9所示。

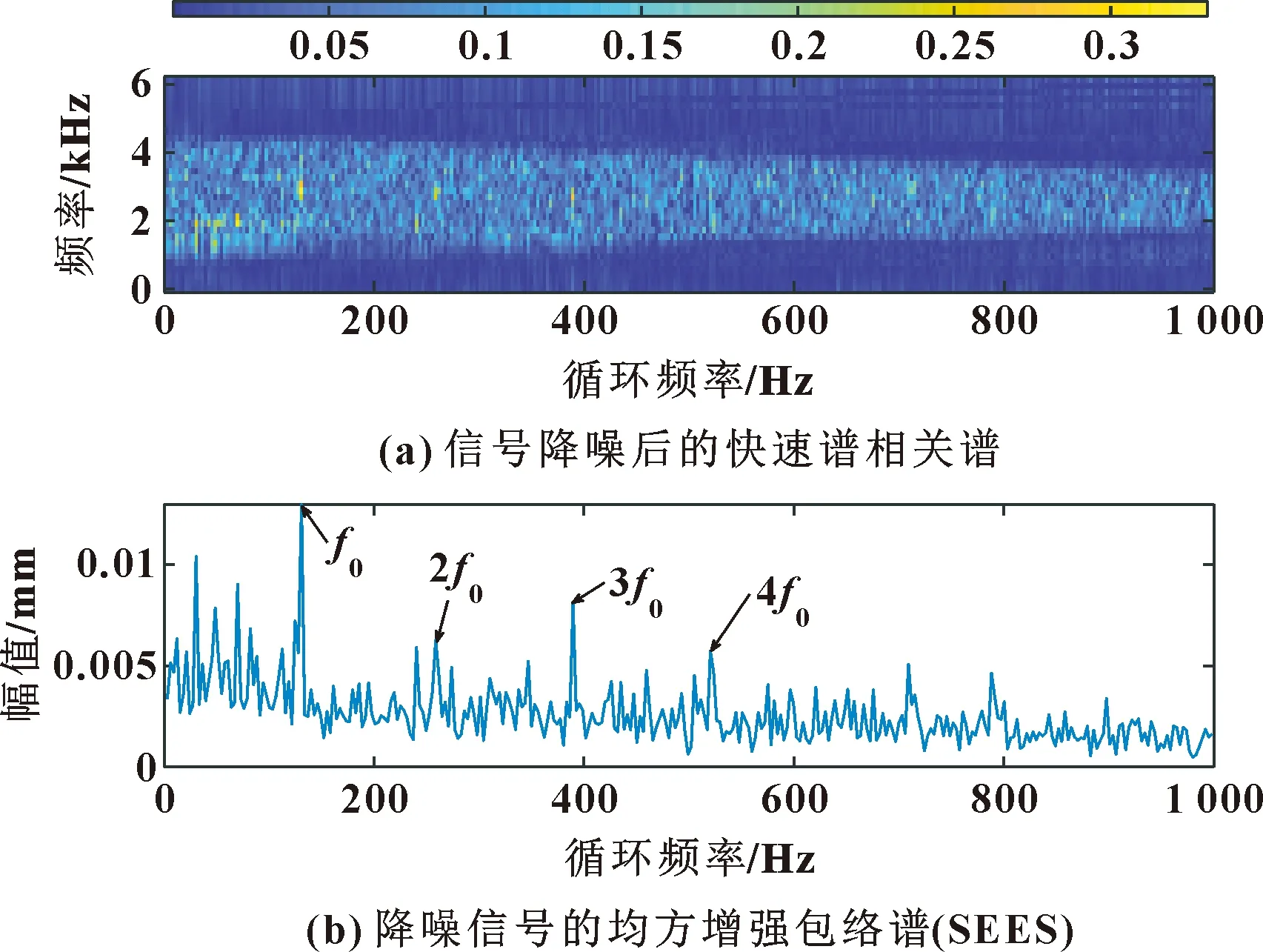
图9 所提方法仿真信号分析结果

由图9可知：在均方增强包络谱中，可清晰地发现外圈故障频率的1～4倍频，准确地判断出外圈发生故障。对比图9和图5可知，采用改进的EWT降噪后的信号进行快速谱相关分析，噪声频率得到了较好的抑制，能快速、准确地识别出早期故障类型。为展示快速谱相关分析增强周期成分的效果，将降噪信号采用Hilbert包络处理，如图10所示。可知：在发现的故障的1～4倍频中，除了3倍频幅值较明显，其余幅值淹没在噪声频率中，易误认为噪声频率。

图10 降噪信号的包络谱

为分析所提方法的优越性，对降噪后的信号采用快速峭度图方法进行分析。图11所示为该方法的分析结果，图12所示为该方法最大峭度频带信号分量的平方包络谱图。谱峭度最大值为0.32，频带中心频率为3 840 Hz，带宽为1 536 Hz，其平方包络谱中发现3倍故障频率，但淹没在噪声频率中，诊断效果较差。这是因为该方法通过计算不同频带的峭度，并采用带通滤波将最大峭度频带提取出来，受噪声影响较大，相比于文中方法，效果较差。

图11 降噪信号的快速谱峭度图

图12 快速谱峭度方法中信号分量的平方包络谱

4 试验信号验证

为进一步分析所提方法的优越性，在Paderborn大学轴承数据集上进行进一步的验证与分析。轴承试验台如图13所示，它由电机、扭矩测量轴、滚动轴承测试模块、飞轮和负载电机模块组成。所有测试试验中包括6个正常轴承、14个采用加速寿命试验损坏的轴承、12个具有人为损坏的轴承。选取加速寿命试验损伤等级为轻度内圈故障振动信号进行分析，失效形式为疲劳点蚀。选取分析的轴承内圈故障信号段的标识为N15_M07_F04_KI17。该标识表示转速为1 500 r/min，加载扭矩为0.7 N·m，径向加载为400 N。

图13 Paderborn大学轴承试验台

采样频率为64 kHz，但轴承的故障信息分布在低频段。为更好地进行早期故障特征提取，进行降采样处理，采样频率为16 kHz，选择前1 s的数据进行分析。图14所示为内圈故障信号的时频域图及包络谱，由文献[11]可知转频为25 Hz，内圈故障频率为123.3 Hz。由图14可以发现1倍转频及2倍故障频率，但其幅值并不明显，淹没在噪声频率中，不能准确判断其故障形式，需进一步降噪处理。

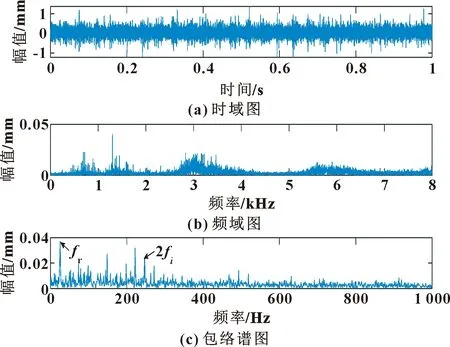
图14 内圈故障信号时频域图及其包络谱

采用所提出的改进EWT进行降噪处理，相关参数设置与仿真信号保持一致，其频带划分及各模态分量分别如图15、图16所示。

图15 改进EWT的频带划分图(试验信号)

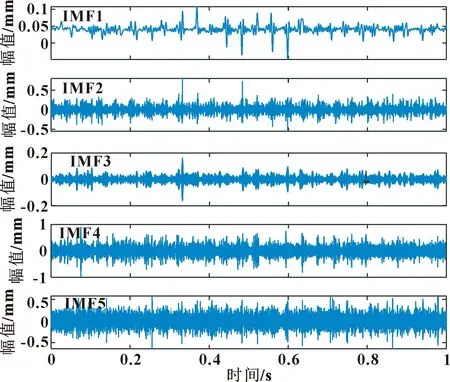
图16 改进的EWT试验信号分解结果

计算各IMF分量的峭度，结果如表2所示。可知前3个分量峭度较大，含有较多的冲击成分，但由图15可知IMF1频带范围较小，相对于IMF2、IMF3含较少的故障信息。因此，选择IMF2和IMF3重构信号作为降噪信号。

表2 各IMF分量峭度

对降噪信号采用快速谱相关分析法增强其周期特征，相关参数设置与仿真信号保持一致，所得结果如图17所示。为说明文中方法的优越性，分别对原始信号进行快速谱相关分析、降噪信号与快速谱峭度分析，结果分别如图18—图20所示。

图17 文中所提方法分析结果

图18 文献[8]方法试验信号分析结果

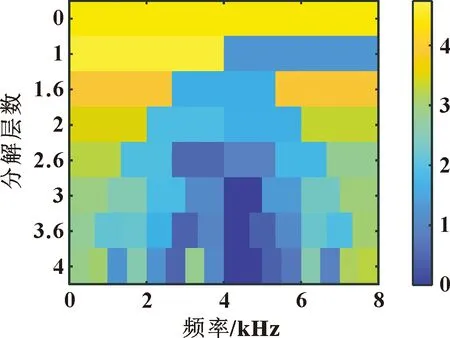
图19 降噪信号的快速谱峭度图(试验)

图20 快速谱峭度图中信号分量的平方包络谱(试验)

由图17可知：文中所提方法较好地提取出了故障特征频率的1～3倍频及转频特征，信号特征幅值较明显，能准确地判断为内圈故障。由图18可知：直接使用快速谱相关对原始信号进行分析，虽能提取出信号中的周期成分，但噪声频率对其影响较大，淹没故障特征频率，不利于准确诊断故障。用快速谱峭度分析降噪信号，结果如图19、图20所示。可知：分解层数为1，带宽范围0～4 000 Hz，谱峭度最大值为4.8，所在频带中心频率为2 000 Hz，带宽为4 000 Hz，其平方包络谱中发现1～2倍故障频率，但幅值并不明显，效果不理想。因此，利用所提方法能实现滚动轴承早期故障的识别。