ARIMA-SVM组合模型驱动下的瓦斯浓度预测研究
2022-10-12范京道黄玉鑫闫振国李川王春林贺雁鹏
范京道,黄玉鑫,闫振国,李川,王春林,贺雁鹏
(1. 陕西延长石 油(集团)有限责任公司,陕西 西安 710075;2. 西安科技大学 安全科学与工程学院,陕西 西安 710054;3. 陕西延长石油巴拉素煤业有限公司,陕西 榆林 719000)
0 引言
瓦斯浓度指标预测以日常瓦斯监测监控数据的统计、分析及挖掘为基础,对瓦斯浓度的变化规律进行研究,是一种预测瓦斯浓度发展趋势的方法[1-3]。常用的瓦斯浓度指标预测方法有神经网络模型法、指数平滑法、灰色系统理论预测法和时间序列预测法等,其中ARIMA(Autoregressive Intergrated Moving Average,自回归滑动平均)模型是研究瓦斯浓度时间序列数据预测的主要方法,但对于非线性数据的分析能力不理想。为解决该问题,许多学者在分析数据过程中融入了较多的非线性数据分析方法[4-5]。刘莹等[6]融合多种环境因素,构建了基于多因素的LSTM(Long Short-Term Memory,长短期记忆网络)瓦斯浓度预测模型,该模型预测效果优于单因素模型,具有较高的预测精度。吴奉亮等[7]构建了基于特征变量选择的随机森林回归模型,并使用该模型对煤矿瓦斯涌出量进行预测,研究表明该方法能够有效提高预测效率和精度。张震等[8]建立了一种基于Keras长短期记忆网络的瓦斯浓度预测模型,该模型较ARIMA模型预测效果好、误差小。周松元等[9]构建了基于TreeNet算法的瓦斯浓度预测方法,并通过测试分析验证了该方法是一种基于机器学习的工作面预测指标的敏感性判别方法,可用于建立煤矿工作面瓦斯突出预测敏感指标体系。上述方法存在单一瓦斯预测模型挖掘矿井瓦斯浓度时间序列全部特征能力较弱的问题[10]。
针对上述问题,将ARIMA模型与支持向量机(Support Vector Machine,SVM)模型融合,对瓦斯浓度进行预测。ARIMA模型可实现对瓦斯浓度时间序列的高精度预测,对线性波动的解释能力较强;SVM模型对非线性特征数据具有较高的预测和泛化能力。首先,利用ARIMA模型处理瓦斯浓度时间序列的历史数据,得到相应的线性预测结果和残差序列。其次,利用SVM模型进一步对数据残差序列中的非线性因素进行分析,得到组合模型预测结果。再次,通过对ARIMA模型与SVM模型分配不同的权重参数,将SVM模型和ARIMA模型分别预测的结果进行线性叠加。最后,通过矿井实测数据与预测结果进行对比,验证组合模型的预测精度。
1 ARIMA-SVM组合模型
1.1 ARIMA模型
ARIMA(p,d,q)模型通过收集、分析过去时间点的观测值来刻画其内在联系,并对过去时间的观测值及误差线性方程进行分析,以实现预测目的[11-12],其中p为自回归阶数,p≥0,d为差分阶数,d>0,q为移动平均的阶数,q≥0。假定时间序列X={xi,i=1,2,…,N},xi为第i个时间序列数据,N为时间序列中数据总数,则ARIMA(p,d,q)为
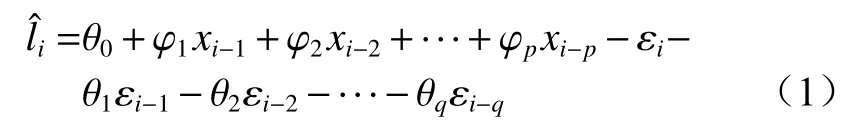
式中:为 第i个线性时间序列数据的预测值;θq和φp为待估计的参数值;εi为预测误差。
1.2 SVM模型
SVM是基于统计学理论的新型机器学习方法[13-14]。假设训练集,其中zA为第A个瓦斯浓度时间序列数据残差的输入,fA为第A个瓦斯浓度时间序列数据残差的输出,则SVM回归模型为
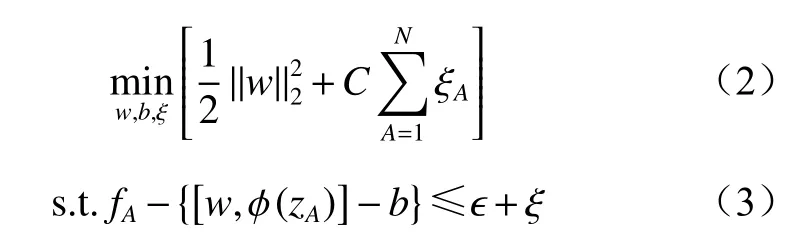
式中:w和b为超平面参数;ξ为松弛变量;C为惩罚因子,C>0;ξA为第A个瓦斯浓度时间序列数据的松弛变量;φ(zA)为映射函数;ϵ为决定间隔边界宽度的超参数。
1.3 ARIMA-SVM组合模型
瓦斯浓度时间序列数据中包含线性和非线性2种趋势,ARIMA模型对于线性部分的数据特征有较强的捕捉能力,而SVM模型在分析和预测非线性数据具有突出性能。假定瓦斯浓度时间序列数据X由线性和非线性2个部分构成,X={xi,i=1,2,…,N}。首先,采用ARIMA模型分析一维瓦斯浓度时间序列的历史数据,得到线性时间序列数据的预测值l和预测时间序列残差数据δi,δi=xi-。其次,采用SVM模型在影响瓦斯浓度时间序列数据的面板数据上进一步分析预测时间序列残差数据δi中的非线性因素,获得非线性时间序列数据预测值。最后,将2个模型分析预测结果进行组合,得到目标瓦斯浓度时间序列数据的最终预测结果
2 实验过程
2.1 数据来源
选取陕北某矿211工作面上隅角2020年9月1-7日共7天的瓦斯浓度数据统计指标作为研究对象。该矿位于榆林市境内,煤层瓦斯含量较低,地质条件变化较小。选取的数据源自同一煤层相同盘区,仅考虑在瓦斯浓度单因素影响下的预测结果。从9月1日0时起开始监测瓦斯浓度,每5 min采集1次,取其平均值,共采集2 016组数据作为实验数据。9月1日采集的原始数据如图1所示,部分数据见表1。
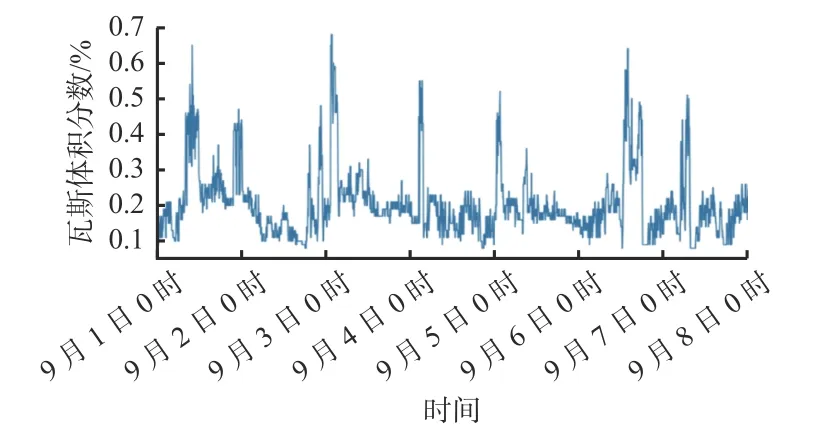
图1 原始瓦斯浓度时间序列Fig. 1 Original time sequence of gas concentration
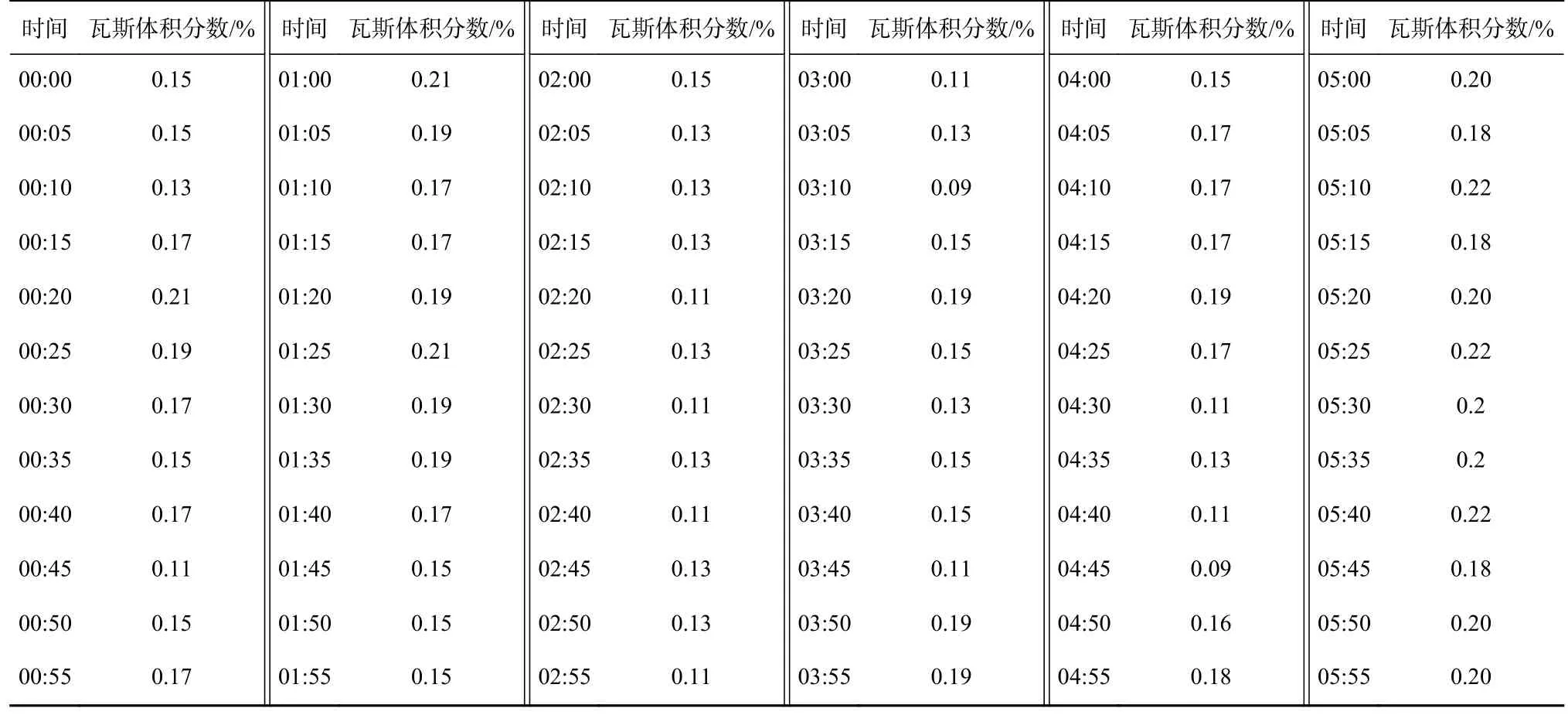
表1 9月1日采集的部分瓦斯浓度数据Table 1 Part of the gas concentration data collected on September 1
2.2 瓦斯浓度预测及拟合效果
2.2.1 ARIMA模型预测
将1 440组数据作为模型的训练集,用于模型参数估计;其余576组数据作为测试集,用于模型泛化能力测试与检验。采用拉依达准则[15](即先假设1组检测数据仅有随机误差,对该数据分析后得到标准偏差,按一定概率构建一个区间,若超过该区间误差,则不属于随机误差而是粗大误差,应将其舍弃)对所采集数据中的异常数据(瓦斯传感器测量值与其平均值之差的绝对值大于其标准差3倍的数据)进行处理,将异常数据替换为其相邻2个数据的平均值。将预处理后的数据进行单位根(Augmented Dickey-Fuller test,ADF)检验处理,如果时间序列平稳,则不存在ADF,否则存在ADF。在ADF检验过程中假设训练集存在ADF,如果得到的显著性检验统计量(T值)小于3个置信度(10%,5%,1% ),则分别对应有90%,95%,99%的把握来拒绝原假设,且T值对应的概率值(P值)小于0.05(最好等于0)时,即可判断为平稳时间序列,否则为非平稳时间序列,利用差分法对非平稳时间序列进行平稳化处理,采用ADF对差分后的序列继续进行检验,直至其达到平稳。ADF检验结果见表2。
由表2可看出,T值为-6.22,小于置信度为1%,5%,10%的临界值,但P值大于0.05,因此判断预处理后的瓦斯浓度数据为非平稳时间序列。对其分别进行一阶差分和二阶差分处理,使其成为平稳时间序列,如图2、图3所示。
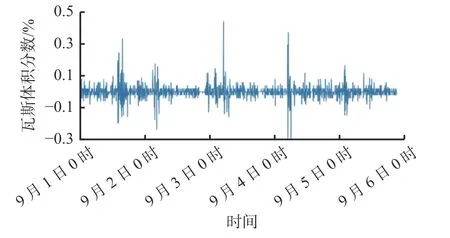
图2 非平稳瓦斯浓度时间序列的一阶差分结果Fig. 2 Result of first-order difference for time series of nonstationary gas concentrations
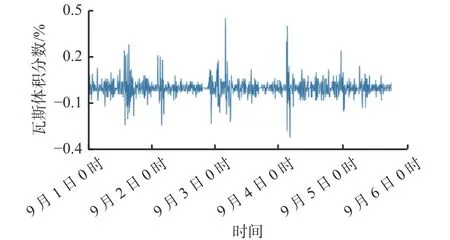
图3 非平稳瓦斯浓度时间序列的二阶差分结果Fig. 3 Results of second-order difference for time series of nonstationary gas concentrations

表2 ADF检验结果Table 2 Result of ADF test
从图2和图3可看出,非平稳时间序列在经过一阶差分、二阶差分处理后数据已趋于平稳,且经一阶差分与二阶差分处理后的瓦斯浓度分布趋势差异较小,均趋于平稳序列。
为进一步判断经一阶差分处理后的时间序列是否为平稳序列,对一阶差分后的序列进行ADF检验,得P值为5.038×10-8,远小于0.05,接近0,因此判断经一阶差分处理后的非平稳时间序列成为平稳时间序列。
数据平稳后使用自相关函数(Autocorrelation Function,ACF)和偏自相关函数(Partial Autocorrelation Function,PACF)为ARIMA模型定阶,如图4所示。可看出ACF和PACF在一阶或二阶后均落在置信区间,因此初步可得ARIMA(1,1,1),ARIMA(1,1,2),ARIMA(2,1,1),ARIMA(2,1,2)4个模型。
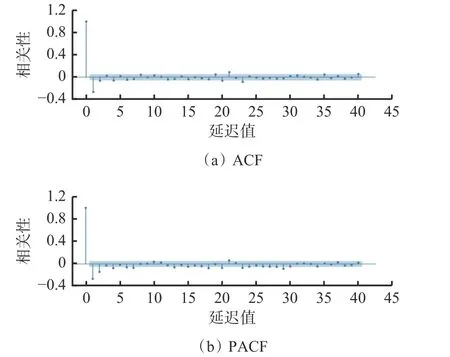
图4 自相关与偏自相关函数Fig. 4 Autocorrelation and partial autocorrelation functions
采用贝叶斯准则(Bayesian Information Criterion,BIC)对模型进行选择,BIC值越小,表示模型越优,将4个模型进行对比并选取最优模型(图5),其中AR0-AR4为自回归模型输出,MA0-MA4为移动平均模型输出。可看出当自回归模型阶数p为1、移动平均模型阶数q为2时,BIC值最小,因此可判断ARIMA(1,1,2)为最优模型。
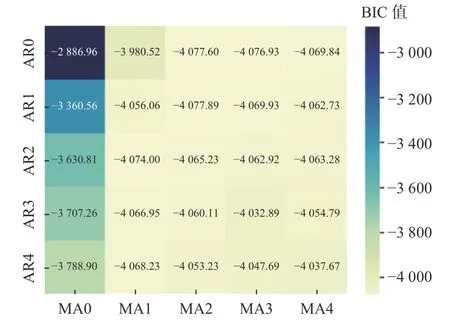
图5 BIC图Fig. 5 BIC diagram
利用Ljung-Box来检验ARIMA(1,1,2)模型的适用性,通过ARMA(1,1,2)模型预测后得到一个新的序列(即预测序列)。如果模型对原始序列解释性很好(即检验结果中P值均大于等于0.05),则预测序列与原始序列的差值(残差序列)是白噪声序列。在本次检验中所有P值均大于0.05,部分P值见表3。这说明预测序列与原始序列的差值是白噪声序列,因此判断模型对瓦斯浓度数据的变化趋势较为适用。采用该最优模型预测9月6,7日的瓦斯数据,结果如图6所示。可看出ARIMA(1,1,2)模型具有较高的拟合度,但与实际数据仍存在一定拟合误差。
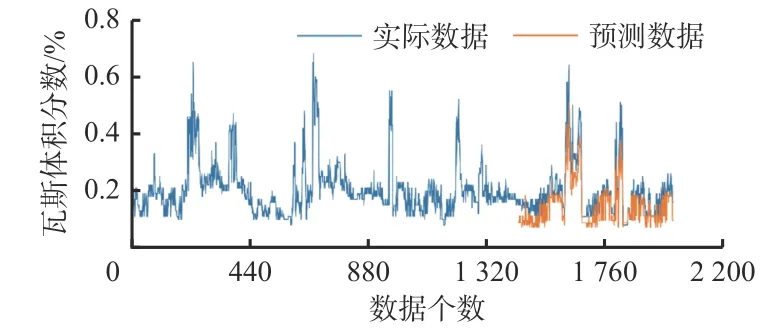
图6 ARIMA模型的瓦斯浓度预测结果Fig. 6 Gas concentration prediction results by ARIMA model
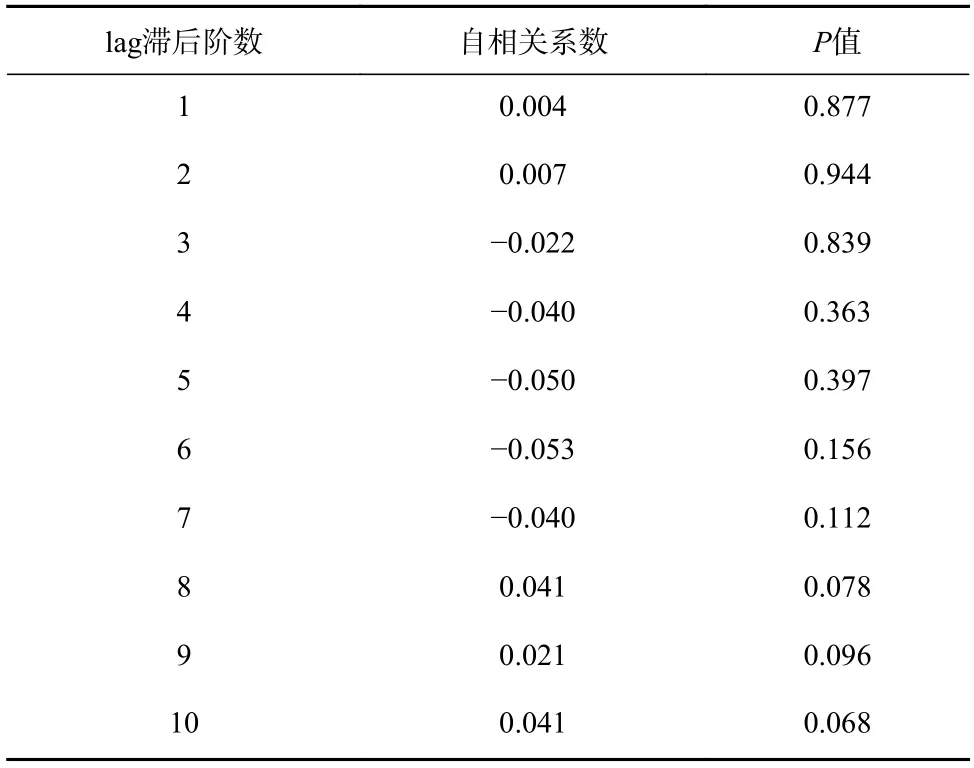
表3 Ljung-Box检验表Table 3 Ljung-Box inspection table
2.2.2 SVM模型预测
利用SVM模型对瓦斯浓度时间序列的非线性部分进行预测,以9月1-5日1 440组数据作为训练集对SVM模型进行训练,对拟合样本进行归一化,在确定最优惩罚因子为72、最优核函数为0.01后,对9月6,7日576组数据进行预测,结果如图7所示。可看出预测结果与实际数据走势相近,但拟合度相对较差。
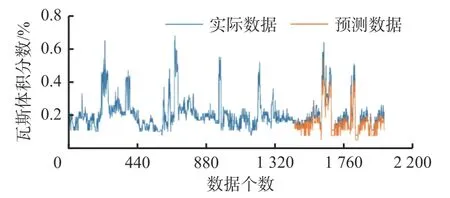
图7 SVM模型的瓦斯浓度预测结果Fig. 7 Gas concentration prediction results by SVM model
2.2.3 ARIMA-SVM模型预测
以9月1-5日1 440组数据作为训练集对ARIMA-SVM组合模型进行训练,通过ARIMA模型处理线性数据,SVM模型处理非线性数据,对ARIMA模型预测误差进行优化,最终通过最优ARIMA-SVM组合模型对9月6,7日576组数据进行预测,结果如图8所示。可看出ARIMA-SVM组合模型预测结果与实际数据的拟合度优于ARIMA模型和SVM模型。

图8 ARIMA-SVM组合模型的瓦斯浓度预测结果Fig. 8 Gas concentration prediction results by ARIMA-SVM combined model
采用ARIMA模型、SVM模型及ARIMA-SVM组合模型对瓦斯浓度数据进行预测分析,结果如图9所示。可看出相对于ARIMA模型、SVM模型,ARIMA-SVM组合模型的误差大幅度减小,且预测结果明显优于单一预测模型。
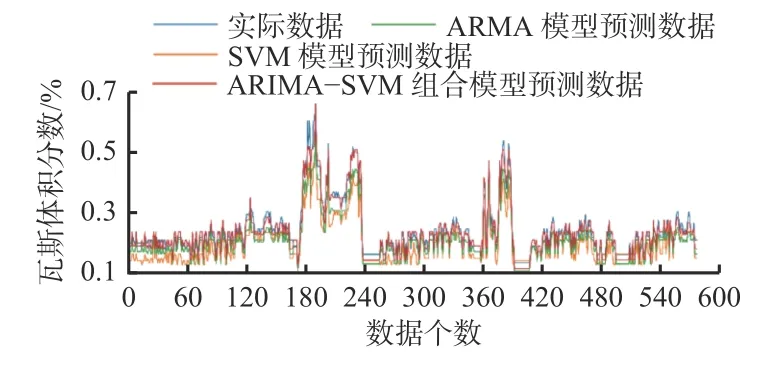
图9 瓦斯浓度预测结果Fig. 9 Prediction results of gas concentration
为更加客观地了解各模型预测精度,采用平均绝对误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)3个指标来衡量各模型预测结果(表4)。
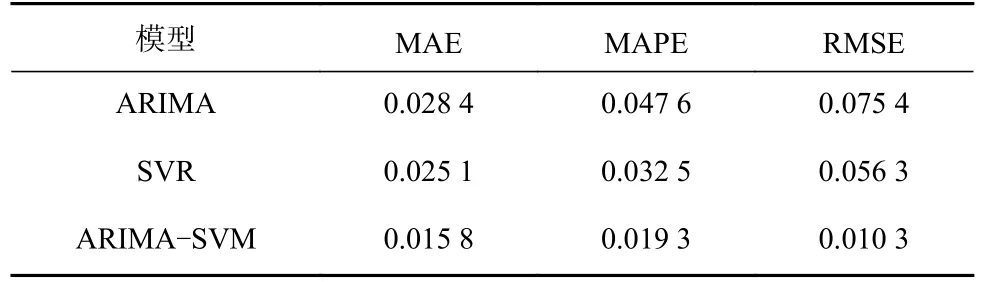
表4 各模型预测结果分析Table 4 Prediction results analysis of each model
从表4可看出,ARIMA-SVM组合模型的MAE,MAPE,RMSE均为最小,说明ARIMA-SVM组合模型预测效果更显著,预测精度更高。因此ARIMASVM组合模型更加适合瓦斯浓度时间序列预测。
3 结语
针对瓦斯浓度时间序列中既有线性趋势又有非线性趋势的数据特征,采用ARIMA模型预测序列中的线性数据,利用SVM模型预测序列中的非线性数据。结合ACF,PACF及BIC准则,得到ARIMA最优模型为ARIMA(1,1,2),根据核函数等参数寻优,确立了最优SVM模型,从而建立了ARIMA-SVM组合模型。利用3种模型对瓦斯浓度进行预测,结果表明:ARIMA-SVM组合模型预测结果与实际数据的拟合度优于ARIMA模型和SVM模型;相对于ARIMA模型、SVM模型,ARIMA-SVM组合模型的误差大幅减小,且预测结果明显优于单一模型;ARIMA-SVM组合模型的MAE、MAPE,RMSE均为最小,ARIMA-SVM组合模型预测效果更显著、预测精度更高,能够综合反映瓦斯浓度时间序列规律,对煤矿瓦斯精准预警具有重要意义。
