煤矿旋转机械健康指标构建及状态评估

李曼，潘楠楠，段雍，曹现刚

（1. 西安科技大学 机械工程学院，陕西 西安 710054；2. 陕西省矿山机电装备智能监测重点实验室，陕西 西安 710054）

0 引言

随着煤矿开采深度和难度不断加大，煤矿设备正逐渐趋于大型化、复杂化和智能化[1-2]。矿用旋转机械所处环境恶劣，工作载荷大且多变，易出现故障，且其振动信号具有非平稳、非线性的特点，使得设备状态监测和准确评估困难。因此，对煤矿旋转机械健康状态进行准确评估，对于保障煤矿机械设备安全高效运行具有重要意义。

设备健康评估方法主要有基于物理模型驱动、基于知识驱动和基于数据驱动的方法[3]。煤矿旋转机械结构复杂，且关键部件的健康状态呈现复杂的退化规律，基于物理模型和知识驱动的方法难以准确建立评估模型。随着信息与传感技术的飞速发展，基于数据驱动的方法已被广泛应用于煤矿设备故障诊断、异物检测和煤矸检测等方面[4]。在设备健康评估方面，基于数据驱动的方法主要包括有监督学习和无监督学习2种方法[5]。有监督学习方法能够建立样本与标签之间的联系，有效地进行分类与回归，但煤矿旋转机械结构复杂、工况多变，难以建立样本与健康状态之间的对应关系，且往往需要大量专家知识与人为经验。无监督学习方法无需费时费力的数据标记过程，能够自适应地进行特征提取与降维，实现设备健康状态评估。在众多无监督学习算法中，卷积自编码器（Convolutional Autoencoder，CAE）模型集成了自编码器（Autoencoder，AE）与卷积神经网络（Convolutional Neural Network，CNN）的优势，能够实现任意维度的特征空间映射[6]，在避免专家经验的同时增强模型性能。CAE虽然有出色的特征提取与降噪能力，但卷积单元仅能提取数据样本的局部空间相关特征，未同时考虑样本的空间与时间特性，存在特征学习不完备的问题，影响识别准确性。

煤矿设备监测参数为时间序列数据，其时序特征对健康评估的影响较大。循环神经网络（Recurrent Neural Network，RNN）能够学习数据中的序列特征，在健康评估与寿命预测中得到了应用。长短期记忆（Long Short-Term Memory，LSTM）网络是一种改进RNN，通过引入门控结构控制信息的传递，从而有效记忆时序数据特征，解决RNN因时间间隔过大出现的梯度消失和梯度爆炸等问题[7]。为充分挖掘煤矿设备振动数据的时间与空间特征信息，本文采用LSTM网络提取振动数据的时间序列特征，建立了基于二维数组的长短期记忆降噪卷积自编码器（Twodimensional array Long Short-Term Memory Denoising Convolutional Autoencoder，2D-LSTMDCAE）模型，并提出了基于2D-LSTMDCAE的煤矿旋转机械健康指标（Health Indicator，HI）构建及状态评估方法。评估模型采用卷积和LSTM并行的网络结构，以二维样本输入，可充分提取振动信号的时空特性。

1 基于2D-LSTMDCAE的HI构建及状态评估方法

1.1 模型构建

1.1.1 LSTM网络

LSTM网络的循环单元结构如图1所示。

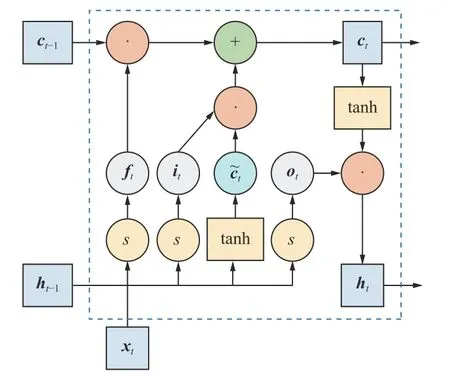
图1 LSTM循环单元结构Fig. 1 Structure of LSTM cyclic unit

LSTM引入输入门it控制当前时刻的候选状态有 多少信息需要保存，引入遗忘门ft控制上一时刻的内部状态ct-1需 要遗忘多少信息，引入输出门ot控制当前时刻的内部状态ct有多少信息需要输出给外部状态ht。 在每个时间步t，隐藏层的状态更新公式为

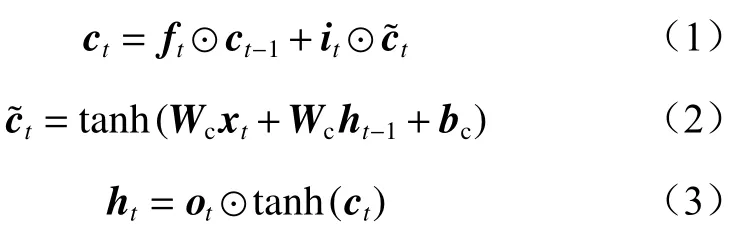
式中：⊙为向量元素相乘符号；tanh为双曲正切激活函数；Wc为候选状态的权重矩阵；xt为当前时刻的输入；bc为候选状态的偏置向量。

3个门的计算公式分别为

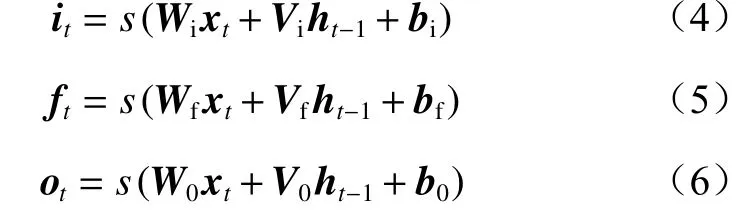
式中：s为Sigmoid激活函数；Wi，Wf，W0分别为3个门中xt的权重矩阵；Vi，Vf，V0分别为3个门中ht-1的权重矩阵；bi，bf，b0分别为3个门的偏置向量。

1.1.2 CAE

CAE由编码和解码2个部分组成，如图2所示。编码部分实现特征提取与降维，解码部分还原特征，并利用卷积、池化、反卷积和上采样代替AE中的全连接层，以增强算法对数据特征的学习能力[8]。

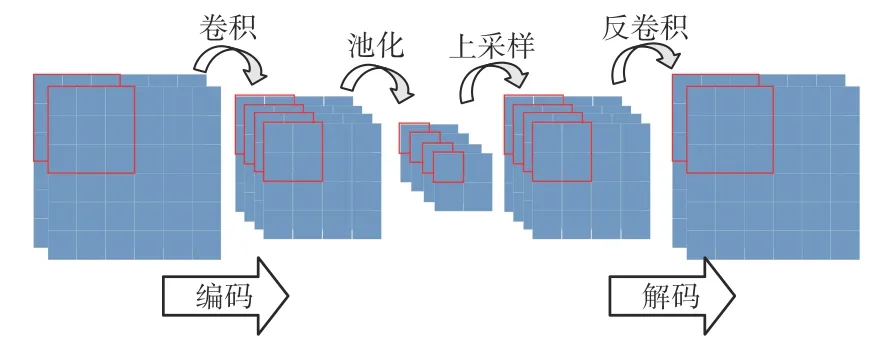
图2 CAE模型Fig. 2 CAE model

1.1.3 LSTMDCAE模型

考虑到实际煤矿生产条件下存在强电磁干扰、载荷多变等因素，使得所测振动信号中包含较强的背景噪声和设备运行引起的机械冲击，所以采用降噪CAE（DCAE）提升模型的降噪能力。LSTMDCAE模型如图3所示。

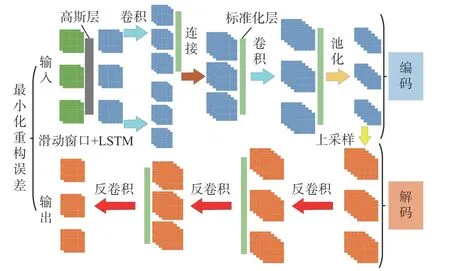
图3 LSTMDCAE模型Fig. 3 LSTMDCAE model

LSTMDCAE模型采用并行多层CAE结构。在编码阶段，分别采用卷积与长短时单元对原始数据集进行特征提取，对提取到的特征进行拼接，再由卷积单元进行特征融合。在解码阶段，采用反卷积和上采样单元将特征恢复为原始数据格式，在输出层之后添加Sigmoid激活函数，将输出特征映射到[0,1]区间，以便于模型训练。

在输入层之后，通过高斯层对输入信号添加噪声，后续通过网络重构无噪声数据，以提高模型的抗干扰能力。在每次卷积后加入标准化层，使每层神经元的输入保持标准正态分布，以避免梯度消失问题，加快模型的训练速度，提高模型的泛化能力[9]。在标准化层后添加ReLU激活函数，使负值置零，以增强模型的非线性能力，加快收敛速度。该模型以无监督的方式从原始数据中捕获时空信息并降低噪声干扰。

1.2 基于2D-LSTMDCAE的HI构建方法

2D-LSTMDCAE模型输入样本及HI构建过程如图4所示。将一维振动数据重构为二维样本，输入由卷积和LSTM组成的并行网络进行样本重构，通过Bray-Curtis距离度量原始样本与重构样本间的相似程度，构建HI，最后通过Savitzky-Golay滤波器对HI曲线进行平滑处理。

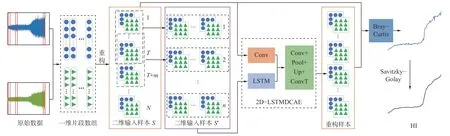
图4 输入样本及HI构建Fig. 4 Construction of input sample and HI

1.2.1 输入样本构建

原始振动信号是一维时间序列信号，通过一维卷积进行特征学习时存在学习能力不足、训练参数较大等问题。将原始数据转换为二维数组，可通过二维卷积网络模型充分学习原始数据中所包含的信息，增强模型对数据特征的学习能力。

首先，分别将垂直和水平2路原始振动数据归一化到[0,1]区间，并切分为等时间长度的N个时刻。其次，按照等间距采样的方式，分别在垂直和水平方向每一时刻的振动数据中取X个数据点，构成2个一维数组，用K1[X]，H1[X]表示。然后，分别将K1[X]，H1[X]重 新排列，重构为长为E、宽为D的2个二维数组，用K2[E×D]，H2[E×D]表示。最后，将任意时刻的2路振动信号二维数组结合为1个二通道输入样本St[E×D×2]，构建N个时刻的总输入样本S[N×E×D×2]，作为卷积单元的输入。

对于输入样本S，以T为窗口长度、m为步长进行滑动，构建输入样本S′[n×T×E×D×2]（n为样本数），作为LSTM网络的输入。

1.2.2 HI构建

基于AE能够重构输入样本的特性，模型在训练时通过最小化重构误差来学习样本数据的分布情况。将设备健康状态下的数据构建为训练样本，输入2D-LSTMDCAE模型中进行训练。随着训练损失的减小，模型能够掌握健康数据的序列特征并学习到数据的深层特征表达。对于健康状态下的监测数据，模型能够很好地对其进行重构，重构样本与原始样本之间的相似度接近于1。当设备开始退化时，振动监测数据中所蕴含的特征信息逐渐偏离健康状态下的特征信息，模型对数据的重构能力逐渐减弱，重构样本与原始样本之间的相似度逐渐减小，当设备失效时，二者之间的相似度为0。重构样本与原始样本之间的相似度差异可以作为健康评估的标准。Bray-Curtis距离是衡量2个物种相似度的指标。向量A=[a1,a2,···,aQ] 与R=[r1,r2,···,rQ] 间的Bray-Curtis距离为

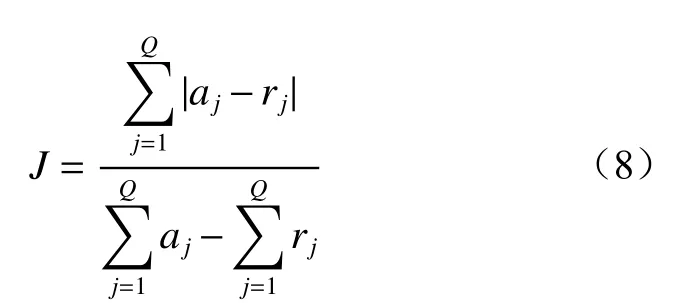
式中：aj，rj为 向量A，R中 的元素；Q为 向量A，R中元素的个数。

相比于欧氏距离，Bray-Curtis距离能够克服因物种丰度引起的误差[10]，衡量特征之间是否存在差异及差异大小[11]。Bray-Curtis距离具有将差异程度归一化的特点，能够消除量纲对度量的影响。采用Bray-Curtis距离衡量重构向量与原始向量之间的相似性，构建反映设备退化情况的HI，可实现旋转机械健康评估。

使用Savitzky-Golay滤波器对得到的Bray-Curtis距离曲线进行平滑，以减小毛刺引起的误报。将平滑后的曲线归一化到[0,1]区间，并将归一化后的值作为HI。HI越趋近于0，表示重构数据与原始数据的偏差越小，设备越健康；HI越趋近于1，表示偏差越大，设备越趋近于失效。

2 模型验证

2.1 数据集选取与样本构建

使用XJTU-SY轴承数据集[12]来验证2DLSTMDCAE模型的特征学习能力。该数据集记录了轴承在3种工况下的全寿命周期数据。实验分别在轴承的水平和垂直2个方向安装加速度传感器，用来采集其振动数据，采样频率为25.6 kHz，每次采样32 768个数据点，采样周期为1 min。各工况下轴承参数见表1。

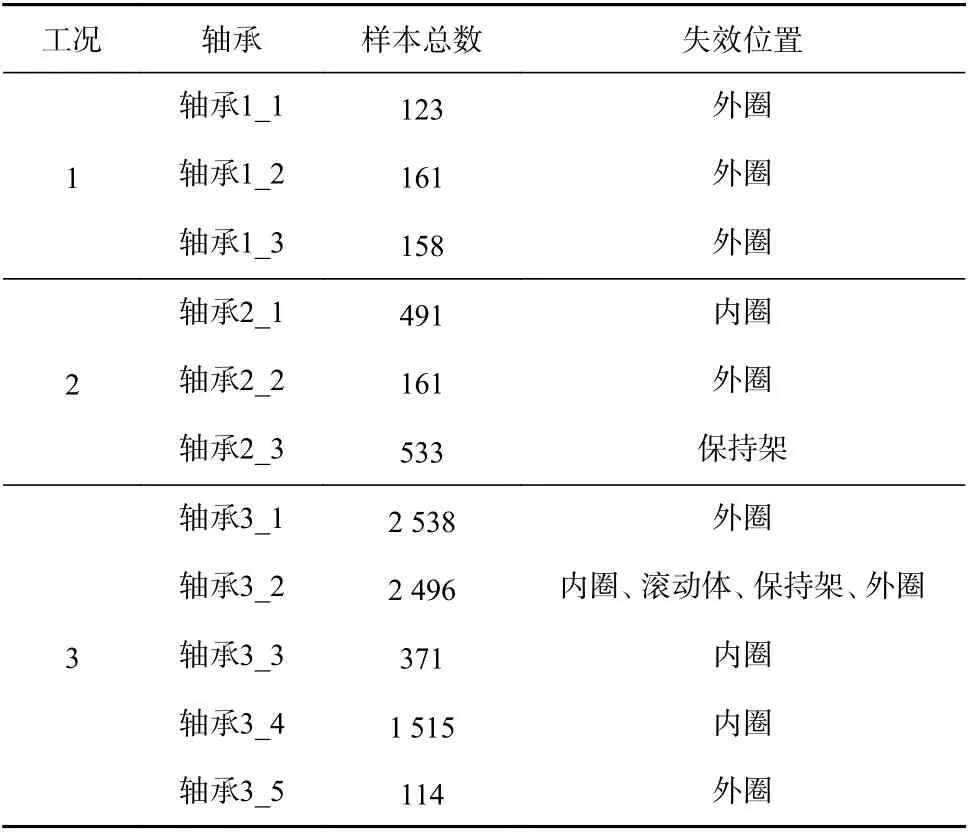
表1 各工况下轴承参数Table 1 Bearing parameters under various working conditions

对XJTU-SY轴承数据集进行处理，对每个时刻下的数据按照等间距采样的方式取16 384个点，构建为1 28×128×2的二通道二维数组格式。采用窗口长度T=10 、 步长m=1 的滑动窗口构建LSTM单元的输入样本。

为测试2D-LSTMDCAE模型的泛化能力，采用同一工况数据训练的模型对不同工况下的轴承进行测试。XJTU-SY轴承数据集中工况3下轴承的退化时间较长，前4个轴承的故障类型包括轴承所有的故障类型，易于找出轴承健康状态下的数据。根据数据集描述可知[13]，实验轴承由开始的健康状态经加速退化实验发展到严重故障状态，工况3下前4个轴承的特征曲线在开始时比较平缓，表明系统运行初期轴承的健康状态良好，可选用工况3下前4个轴承前10%的数据作为训练集[14-15]。使用工况1和工况2下前3个轴承、工况3下第5个轴承（共7个轴承）的全寿命周期数据作为测试集。

2.2 轴承HI曲线构建与分析

采用Adma作为优化器优化网络模型，学习率和batchsize分别设置为0.01和16，训练轮次设置为500。选用Huber损失函数。

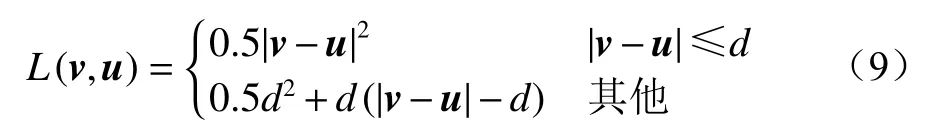
式中：L为损失值；v为 模型输入；u为模型输出；d为常量，d=0.5。

Huber损失函数集成了均方误差和平均绝对误差损失函数的优点，当误差小于0.5时采用平方误差，当误差大于0.5时采用线性误差，能够减小模型对离群点的敏感程度。采用训练集对2D-LSTMDCAE模型进行离线训练，损失曲线如图5所示。可看出损失曲线收敛速度较快，在500次迭代后的损失为4.992 2×10-5，表明模型能够很好地还原健康状态下的样本。

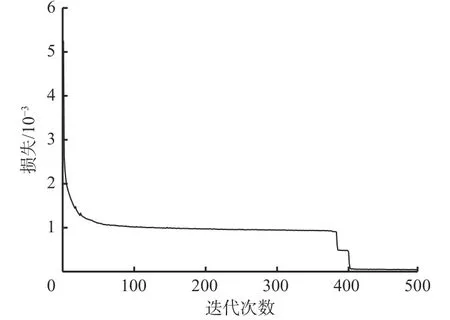
图5 损失曲线Fig. 5 Loss curve

7个测试轴承的Bray-Curtis距离曲线和滤波后得到的HI曲线如图6所示。可看出HI在初始阶段均接近于0，表明各轴承运行状况良好，然后开始缓慢上升，最后均逐渐趋近于1，表明轴承都出现严重故障，与轴承加速寿命试验结果一致。

图6 测试轴承Bray-Curtis距离与HI曲线Fig. 6 Bray-Curtis distance and HI curves of test bearing

2.3 HI评价

为了评估模型能否更早地发现早期故障，采用3σ准则独立计算每个轴承的退化起始阈值，并采用相关性和单调性2个指标评价HI。相关性量化了HI与时间的相关关系，单调性反映了HI的趋势，2个指标的值越大，表明基于HI的状态评估方法性能越好。相关性C和单调性M计算公式分别为

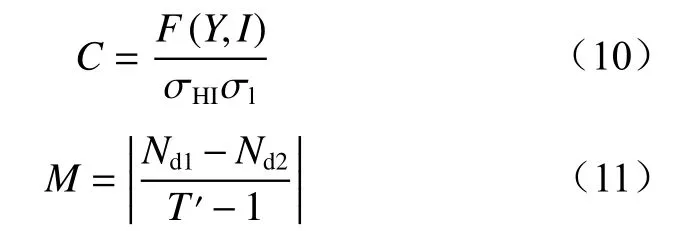
式中：F(Y,I)为Y和I之间的协方差，Y为HI的值，I为构建HI时所对应的时间点；σHI和σl分 别为Y和I的标准差；Nd1，Nd2分 别为Y的微分大于0和小于0的个数；T′为 轴承全寿命周期中HI的长度。

为验证2D-LSTMDCAE模型的有效性和基于HI的状态评估方法的性能，选择经典评价指标均方根与所提HI进行对比实验。为了降低噪声及采用单路数据进行评估对验证结果的影响，计算均方根前对原始数据进行小波降噪（小波函数为sym8，分解层数为5），并对2路信号的均方根取平均值。为评估本文所提样本构建方法的有效性，与无样本重构的LSTMDCAE模型进行比较。为验证LSTM模块的有效性，与DCAE进行比较。构建2D-LSTMDCAE，LSTMDCAE和DCAE共3种AE模型。各模型结构相同，使用相同的训练集和测试集进行验证，且都能够从原始数据中学习特征并重构数据，从而构建HI。3种AE模型构建的HI、均方根指标及通过3σ准则求出的异常状态阈值如图7所示。可看出在轴承1_1上，2D-LSTMDCAE模型所构建的HI在第72 min时超过阈值，LSTMDCAE模型构建的HI、DCAE模型构建的HI和均方根分别在第76，77，78 min时超出阈值，平均比本文所提方法晚5 min。2D-LSTMDCAE在其他6个测试轴承上的表现类似，较其他3种模型指标都能更早找出轴承初始劣化点，在各轴承上分别平均提前了8，11，2，6，14，2 min，平均提前了约7 min。测试结果表明本文所提出的样本构建方法及学习数据时序特征的HI构建方法对轴承的性能退化更敏感，能够更好地描述设备的退化过程。

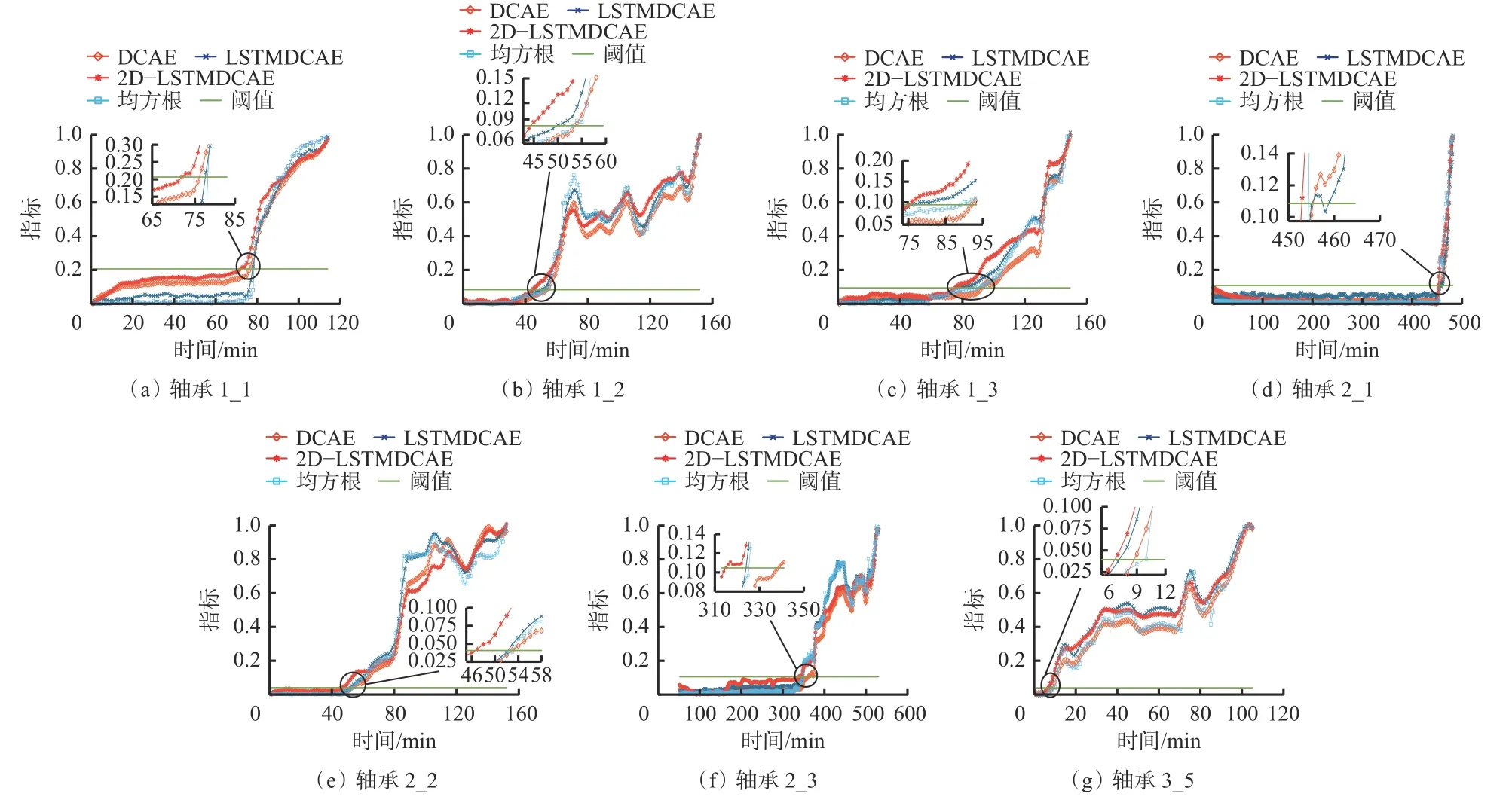
图7 各模型构建的HI对比Fig. 7 Comparison of HI constructed by each model

HI的评价指标见表2。可见，本文构建的HI的相关性比LSTMDCAE，DCAE模型构建的HI和均方根分别高出了0.015，0.031和0.047，单调性分别高出了0.072，0.084和0.272。

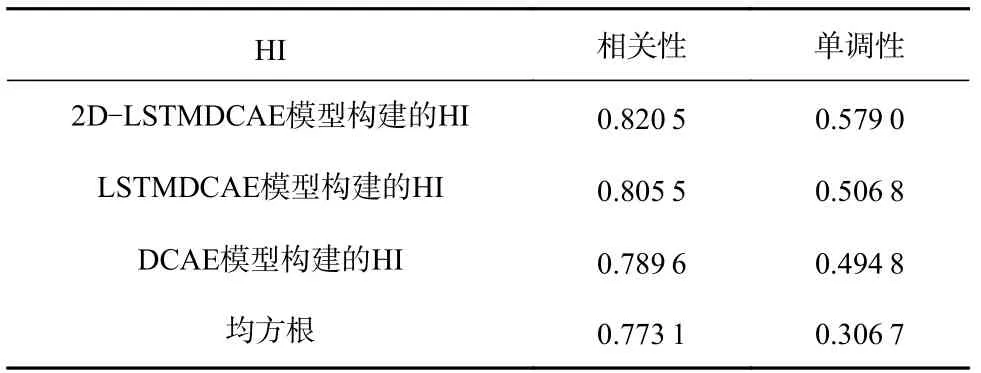
表2 HI的评价指标Table 2 The evaluation index of HI

4种HI的评价指标分析如图8所示。可看出2D-LSTMDCAE模型构建的HI仅在轴承2_1上的单调性比均方根略低一些，在其他轴承上的2种评价指标均高于均方根。与LSTMDCAE相比，2D-LSTMDCAE模型构建的HI在轴承1_3上的2种评价指标、在轴承2_1上的相关性和在轴承2_3上的单调性较低。与DCAE相比，2D-LSTMDCAE模型构建的HI在各轴承上的评价指标均较高。分析结果表明，2D-LSTMDCAE模型构建的HI能更好地反映轴承的退化情况。

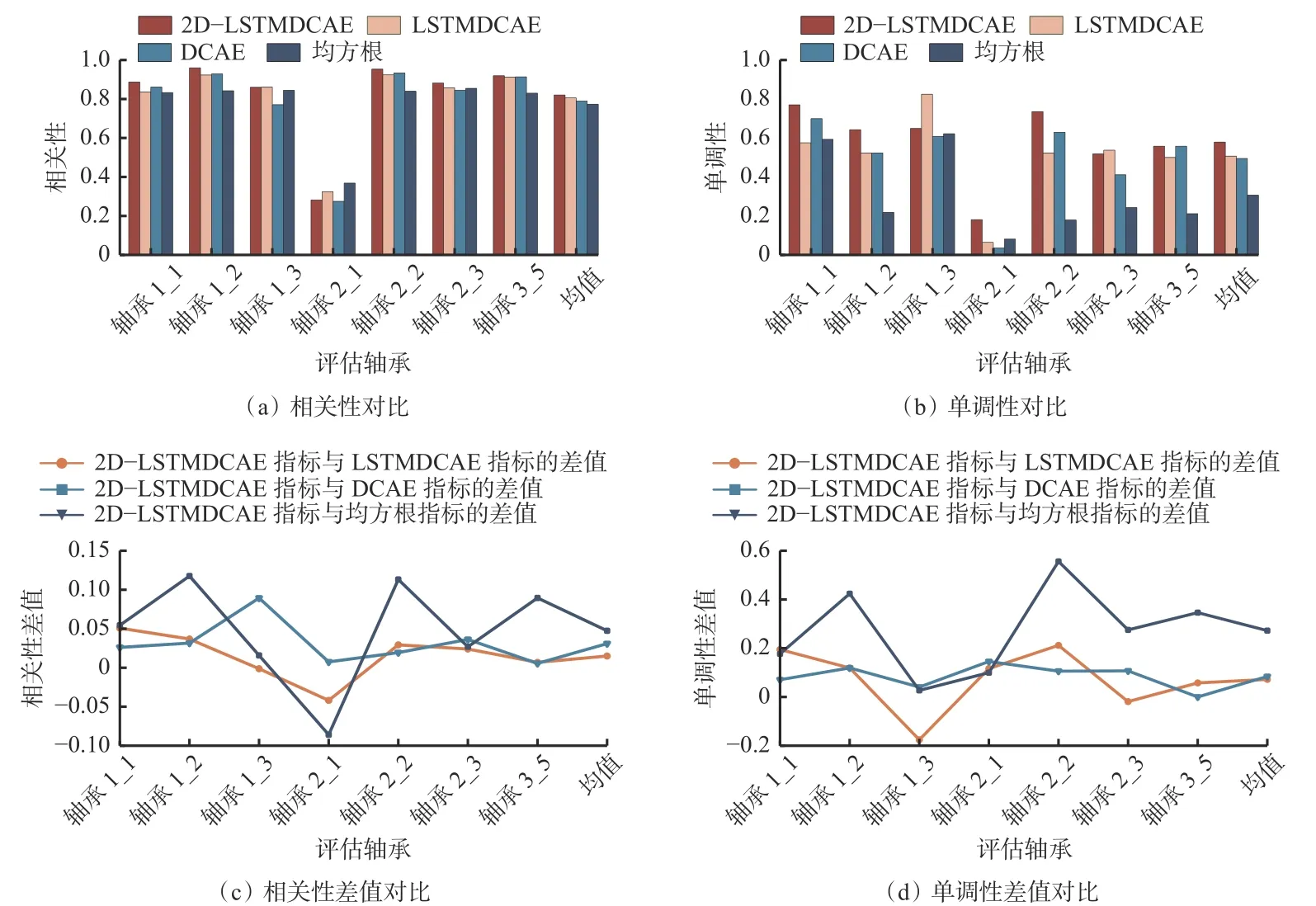
图8 HI的评价指标分析Fig. 8 Analysis of HI evaluation index

2.4 模型对比

为评估模型性能，分别与基于注意力机制的一维深度可分离卷积模型[16]和深度残差模型[17]进行对比实验。考虑到数据样本的无标签特性，对2种模型结构进行适当调整，分别构建基于注意力机制的一维深度可分离卷积自编码器（1D-Attention Depthwise Separable Convolution Autoencoder，1D-ADSCAE）模型和深度残差自编码器（Deep Residual Autoencoder，DRAE）模型。各模型采用相同的数据集进行验证，都能在一定程度上对输入样本进行还原，能够基于AE的重构误差原理构建HI。3种模型构建的HI的评价指标见表3。

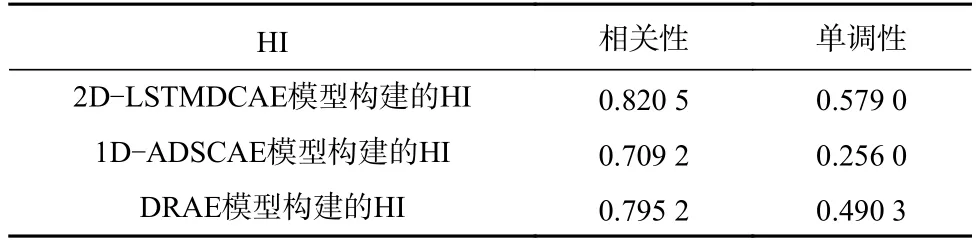
表3 3种深度学习模型构建的HI的评价指标Table 3 Evaluation index of HI constructed by three deep learning models

由表3可看出，2D-LSTMDCAE模型构建的HI具有更好的相关性和单调性，验证了采用卷积与长短期单元并行提取特征并采用卷积进行深层特征学习的2D-LSTMDCAE模型性能更优。

3 实验验证

3.1 实验台搭建与数据采集

在实验室搭建减速器平台，并以煤矿实际工况运行数据为依据模拟采煤机截割传动系统运行状况。实验平台包括齿轮减速器、驱动电动机、磁粉制动器等，如图9所示。在减速器垂直和水平方向分别布置加速度传感器，采集运行过程中的振动信号。

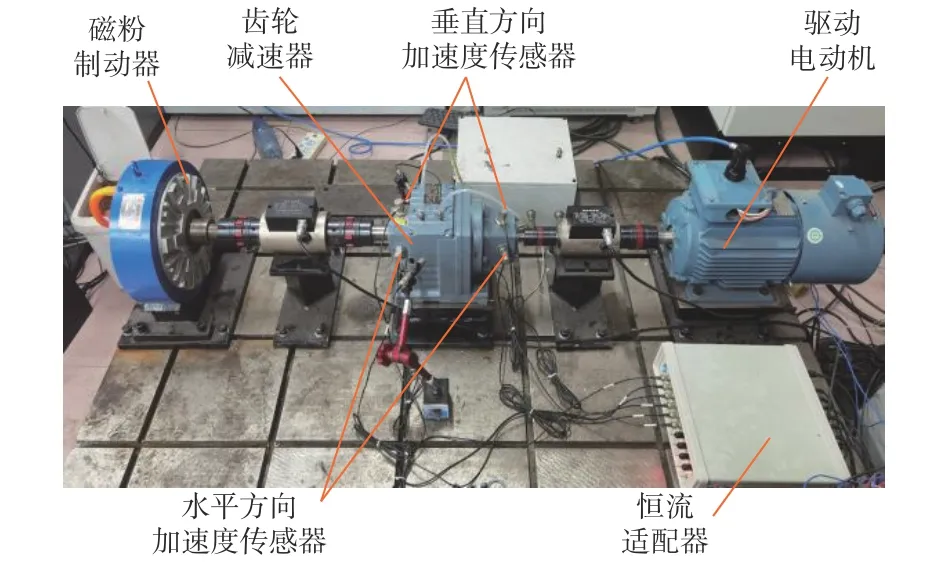
图9 模拟采煤机截割传动系统的减速器平台Fig. 9 Reducer platform simulating shearer cutting transmission system

选取实际工况下采煤机运行1个工作周期的负载变化数据作为激励信号，等比输入磁粉制动器，模拟采煤机截割变负载工况，对减速器进行加速退化实验。实验中振动信号采样频率为5 kHz，监测并记录减速器垂直和水平方向的振动数据。实验结束时，振动信号具有明显幅值波动，波动范围为正常运行时的3～6倍，并且现场出现明显噪声，因此判定减速器完全故障。减速器振动原始信号如图10所示，实验中每分钟采集1组状态值，滤除现场干扰，共采集1 430组退化实验数据。

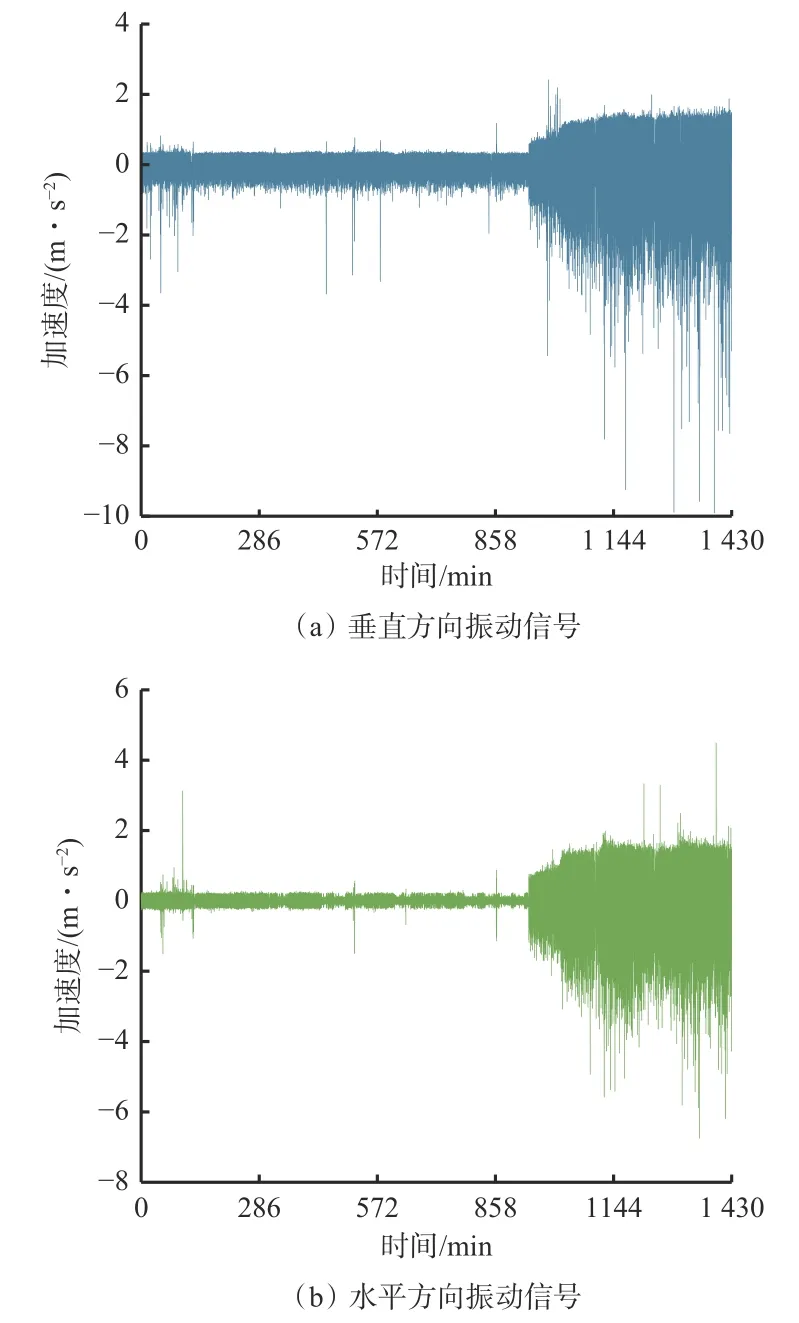
图10 减速器垂直和水平方向原始振动信号Fig. 10 Vertical and horizontal original vibration signals of the reducer

3.2 减速器HI构建与分析

采用减速器加速退化实验数据进行健康评估实验，通过本文所提出的样本构建方法构建训练和测试样本，采用训练样本训练2D-LSTMDCAE模型，将测试样本输入模型中进行评估实验。计算减速器退化数据的均方根指标，与2D-LSTMDCAE模型构建的HI进行对比，实验结果如图11所示。2种HI的评价指标见表4。

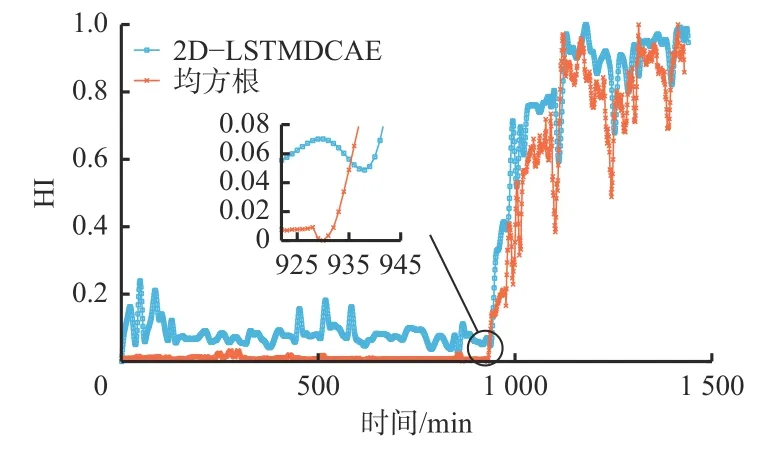
图11 减速器HI对比Fig. 11 HI Comparison of the reducer

表4 减速器HI的评价指标Table 4 HI evaluation index of the reducer

从图11可看出，均方根指标在减速器的健康阶段波动较大，容易造成误报，且在第938 min开始出现上升趋势。2D-LSTMDCAE模型构建的HI在减速器的健康阶段比较平稳，在第930 min开始出现逐渐上升趋势，相比于均方根指标提前了8 min。从表4可看出，2D-LSTMDCAE模型构建的HI更优，表明本文所提方法能够更好地反映减速器的退化情况。

4 结论

（1） 2D-LSTMDCAE模型能够更早地检测到设备的早期故障，在测试轴承上相比于LSTMDCAE和DCAE模型构建的HI及均方根平均提前了约7 min。

（2） 2D-LSTMDCAE模型构建的HI相关性较均方根提升了0.047，单调性提高了0.272，与LSTMDCAE和DCAE构建的HI相比，相关性分别提升了0.015和0.031，单调性分别提升了0.072和0.084。与其他深度学习网络模型构建的HI对比，2D-LSTMDCAE模型仍具有较大的性能优势。

（3） 在测试减速器上，相比于均方根指标，通过2D-LSTMDCAE模型构建的HI能够提前8 min发现早期故障，且HI相关性提高了0.007，单调性提高了0.211。2组实验表明2D-LSTMDCAE模型具有良好的泛化性，是一种良好的HI构建模型。