Bi3+掺杂体系的发光机理：第一性原理研究

楼碧波，尹 民

（1.重庆邮电大学 光电工程学院，重庆 400065；2.中国科学技术大学 物理学院，安徽 合肥 230026）

1 引 言

随着基质材料的改变，掺杂入固体中的Bi3+离子可提供深紫外、可见乃至近红外光谱范围的发射，因而常被用作发光材料的激活离子[1-4]。同时Bi3+离子也常用作敏化剂，通过共掺改善稀土等离子掺杂体系的发光性能。Bi3+离子基电子组态为[（Xe）4f145d10]6s2，其激发电子组态主要具有如下形式：6s16p1电子组态、配体-掺杂离子电荷迁移态（6s26p1加束缚空穴）、金属-金属电荷迁移态（6s1加束缚电子）以及电子在离子对间迁移形成的Bi2+-Bi4+离子对等。这些激发电子组态容易受到基质晶格的影响，它们与Bi3+离子基电子组态之间的吸收和发射相较于三价稀土离子f-f跃迁，将呈现较大的展宽和斯托克斯（Stokes）位移。通过合理选择基质材料以及操控合成条件等，Bi3+离子的光谱性能是可被调控的，如ABZn2Ga2O7∶Bi3+（A=Ca,Sr;B=Ba,Sr）、Cs2Ag0.6Na0.4InCl6∶Yb3+/Er3+/Bi3+、

XAl12O19（X=Ba，Sr，Ca）∶Bi3+体系[5-7]，有望应用于白光照明、X射线探测和生物成像等领域。此外，一些Bi3+掺杂发光材料还具备长余辉发光现象，如CaWO4∶Bi3+、KGaGeO4∶Bi3+，在光催化、防伪、消毒等领域可拥有一定的应用前景[8-10]。

Bi3+离子在玻璃光纤、荧光粉和晶体等体系中的诸多发光现象已被实验研究并广泛报道[1-4]。如Krasnikov等[2]对Bi3+离子各类光跃迁的特征进行了整理分析，总结了指认发光跃迁起源的常见光谱测量方法：激发/发射光谱、发光寿命、发光的浓度或温度依赖关系。Dang等[3]分析总结了Bi3+掺杂发光材料的光谱调控策略，如调节多格位体系中Bi3+离子的占据、选择性激发发光中心、改变掺杂浓度以及通过共掺离子实施能量传递设计。Li等[11]在Ca5（BO3）3F体 系 中 比 较 了Bi3+离 子 所 占据的三个不等价Ca2+格位的配位环境，分析了测量的实验光谱，并展示了电子云重排效应及晶体场对材料发射波长的影响。大量和长期的实验数据分析与总结[12-14]已经确认了发光材料研究中最本质的关系，发光中心的局域环境主要决定能级结构性质以及材料的发光性能。基于此，人们尝试构建经验的构效关系模型，并用于预测Bi3+掺杂发光材料的发光性质。如Boutinaud等[12-13]参考稀土光谱理论，综合分析发光中心与配体之间的相互作用，通过拟合实验数据，获得了Bi3+离子光跃迁能的经验公式，而Dorenbos[14]则进一步经验地确定了Bi-6s及-6p轨道相对基质带边的位置。经验模型可以给出一系列材料中Bi3+发光性能的变化趋势，但对于具体材料中的复杂光谱指认存在一定的困难。例如，Swart[15]指出室温下YPO4∶Bi3+和LaPO4∶Bi3+的激发光谱具有多个峰值，光谱指认存在困难，同时Boutinaud的经验公式分析、Dorenbos的能级结构模型计算以及实验光谱的直接指认三者之间也存在部分不自洽。上述思考引发了我们进一步从第一性原理角度对Bi3+掺杂发光材料的光谱特性开展非经验的理论理解，以支撑相关的实验研究，同时促进和实现对新型Bi3+掺杂发光材料的设计和性能改进。

基于密度泛函理论的第一性原理方法可以对含有点缺陷的发光材料的结构、电子和光学性质进行有效的计算模拟[16-17]。过去十多年里，局域缺陷态的第一性原理计算[18]以及伴随发展起来的光谱学理论已经很好地应用到各类光学材料（稀土离子发光、过渡金属离子发光、自陷激子态发光[19]以及本征缺陷发光[20]）发光机理的解释和发光性能的设计。Sun等[1]认为，对于Bi3+掺杂发光材料的研究，需要建立可靠的Bi3+发光性质与局域结构、基质带隙等之间的联系，同时也需要有清晰的发光过程的物理图像。近来，该第一性原理计算方法已被我们成功地扩展到了Bi3+掺杂发光材料[21-25]，并在若干代表性的体系中对Bi3+离子基态和激发态的几何与电子结构性质给予了较好的理论描述，同时借助于位形坐标模型也实现了激发、弛豫以及发射的动力学过程的数值分析与讨论。

本文将从Bi3+离子光谱学特征的实验指认出发，在能级结构图像和位形坐标图的基础上，首先对Bi3+离子基组态6s2与四类激发组态（即6s16p1电子组态、配体-掺杂离子电荷迁移态6s26p1加束缚空穴、金属-金属电荷迁移态6s1加束缚电子以及电子在离子对间迁移形成的Bi2+-Bi4+离子对）间的光跃迁过程进行了系统总结。其次，我们针对上述每种跃迁类型，逐一介绍相关的理论计算方案。最后，我们以若干代表性例子作为依托，充分展示了有关理论和计算对实验现象的分析和指引作用。此外，从发光性能预测的角度，我们也分析了Bi3+离子发光性质与配位环境、基质带隙、缺陷能级等之间的关联。

2 Bi3+的光谱特征和跃迁过程

Bi3+离子的发光通常处于蓝光及绿光范围，在一些材料中可以产生紫外及近红外发射。结合Krasnikov对Bi3+离子光跃迁特征的 理解[2]，Bi3+离子的光跃迁根据其光谱、温度及浓度响应特性分为以下两大类：（1）具有较小半高全宽（0.3 eV）及Stokes位移（～0.7 eV）[26]、低温环境中（4.2 K）寿命在毫秒量级且随着温度上升（40～100 K）寿命保持不变，进一步升高温度则出现发光寿命骤减、在一定范围内发光强度随掺杂浓度呈现线性变化的发光[2]，例如Y3Al5O12∶Bi3+体系中能量为4.0 eV的发射[27]源自于3P0,1激发态。其机理及过程可理解为 如 下:Bi3+离 子 具 有6s2基 电 子 组 态（1S0），而6s16p1激发组态则由于自旋轨道耦合以及交换作用分裂为单重态1P1以及三重态3P0,1,2。基态1S0到单重态1P1的跃迁在实验上通常对应到真空紫外区域的强吸收，而吸收完成后往往会经历较高1P1激发态能级到更低三重态能级的无辐射弛豫，再之后观测到从三重态3P0,1到基态1S0的发射。这样的发射形式上看起来是自旋禁戒的，但由于旋轨耦合导致的自旋量子态混合使得光发射跃迁成为可能。低温环境（＜100 K）中，发射一般源自于最低的3P0态，其具备较长的发光寿命（～102ms）。室温下，3P1与3P0之间的能量间隔通常在0.2 eV以内，发射可以同时包含3P0,1态，这使得发光寿命骤减。此外，由于3P0,1态到1S0的发射本质应该理解为Bi3+离子6s和6p轨道之间的跃迁，所引起的结构弛豫相对较小，因而光谱的半高全宽及Stokes位移较小。观测到的跃迁能量也同样相对稳定，实验上常将该类型发射记作A带。（2）相较于A带跃迁，具有明显更大的半高全宽[2]和Stokes位移、发光寿命在更低的温度（～6 K）出现骤减并持续降低直到100 K左右，例如Y3Al5O12∶Bi3+体系中能量为2.7 eV的发射[27]，一般可指认为类激子态型。其发光机理及过程如下：固体中掺杂的Bi3+离子可以扮演电子或空穴陷阱，使得Bi3+离子在作为发光中心时拥有电荷迁移态的激发形式。稀土Eu3+离子掺杂体系被激发，可以形成Eu2+离子结合一个束缚空穴的激发态Eu2++hVBM（VBM表达了空穴位于价带顶），进而产生电荷迁移态跃迁[28]。类似地，Bi3+掺杂体系同样可以发生该过程：Bi3+↔Bi2++hVBM，也即配体-掺杂离子电荷迁移态（6s26p1加束缚空穴）与基组态6s2之间的跃迁（CT）。一些体系中，Bi3+离子还可以形成Bi4+离子（6s1）加一个被束缚在导带底附近的电子的组合激发态，也即Bi3+↔Bi4++eCBM，其中CBM代表导带底。由于导带底主要由金属阳离子的轨道成分组成，因而该过程对应到Bi3+阳离子与基质阳离子之间的电荷迁移，常被记作金属-金属电荷迁移态跃迁（MMCT）。由于类激子态的激发三重态中最低能级与亚稳态能级间能隙极小（～1 meV）[29]，因而发生寿命变化的温度极低。其次，跃迁过程涉及电荷迁移，发光中心的有效电荷产生较大变化，因而其配体环境的结构弛豫通常比A带发射更大，表现为更大的Stokes位移以及宽包发射的特性。同时，MMCT与CT跃迁涉及组成带边成分的基质离子，其跃迁能量极容易受基质成分改变的影响。此外，在类激子态中，有一类由于离子团聚或是能量传递实现的Bi3+离子对之间的电荷迁移态跃迁（IVCT）值得单独一提：即Bi3++Bi3+↔Bi2++Bi4+[30]。在一定范围内，这类发射的发光强度随掺杂浓度的增加呈现超线性变化。同时，在 一 些Bi3+发 光 材 料 中，例 如YPO4∶Bi3+[31]、CaSb2O6∶Bi3+[32]，IVCT跃迁的激发光谱特征接近孤立Bi3+离子的A带，且发射谱中经常伴随有A带发射。

第一性原理计算通过构建位形坐标图，可以对上述Bi3+离子跃迁进行准确描述，并给出清晰的激发、弛豫和发射过程。根据Franck-Condon原理，激发为基态平衡几何构型下体系从初态到末态的跃迁，实验通常可以观察到若干个激发峰，对应于图1中位形坐标图的黑色实线。然而，主要的发射源自于结构弛豫后能量最低的激发态，此处为3P0,1态。MMCT和CT对应的高激发态并不稳定，其势能面与最低的A带激发态势能面交错且势垒较小，很容易弛豫到最低的3P0,1激发态并形成A带跃迁为主的发光。位形坐标图展示的跃迁过程也可以呈现在包含带边的能级结构图中。图1中的ϵ（+4/+3）为Bi3+离子的电荷转变能级，即Bi3+离子热离化一个6s轨道电子转变为Bi4+离子所对应的单电子能级。ϵ（+4/+3）与价带顶之间的能隙对应于Bi3+离子扮演作空穴陷阱的陷阱深度，而与导带底之间的能量差则可用于近似Bi3+离子MMCT跃迁（Bi3+↔Bi4++eCBM）的零声子线。同理，ϵ（+3/+2）为Bi3+离子在6p轨道上俘获一个电子转变为Bi2+离子所对应的单电子能级，其与导带底之间的能隙为Bi3+离子扮演作电子陷阱的陷阱深度，而与价带顶之间的能量差则可用于近似Bi3+离子CT跃迁（Bi3++eVBM↔Bi2+）的零声子线。类似地，通过A带的零声子跃迁能，我们给出了3P0,1激发态在禁带中对应的能级位置并记作ϵ（+4/+3*）。其 中，A带 和MMCT态 的 零 声 子 线 都 涉 及相同的ϵ（+4/+3）转变能级。IVCT则为一对近邻Bi3+离子之间的电荷迁移，其零声子线可通过ϵ（+4/+3）和ϵ（+3/+2）之间的能差近似（未考虑离子对之间的库伦作用）。

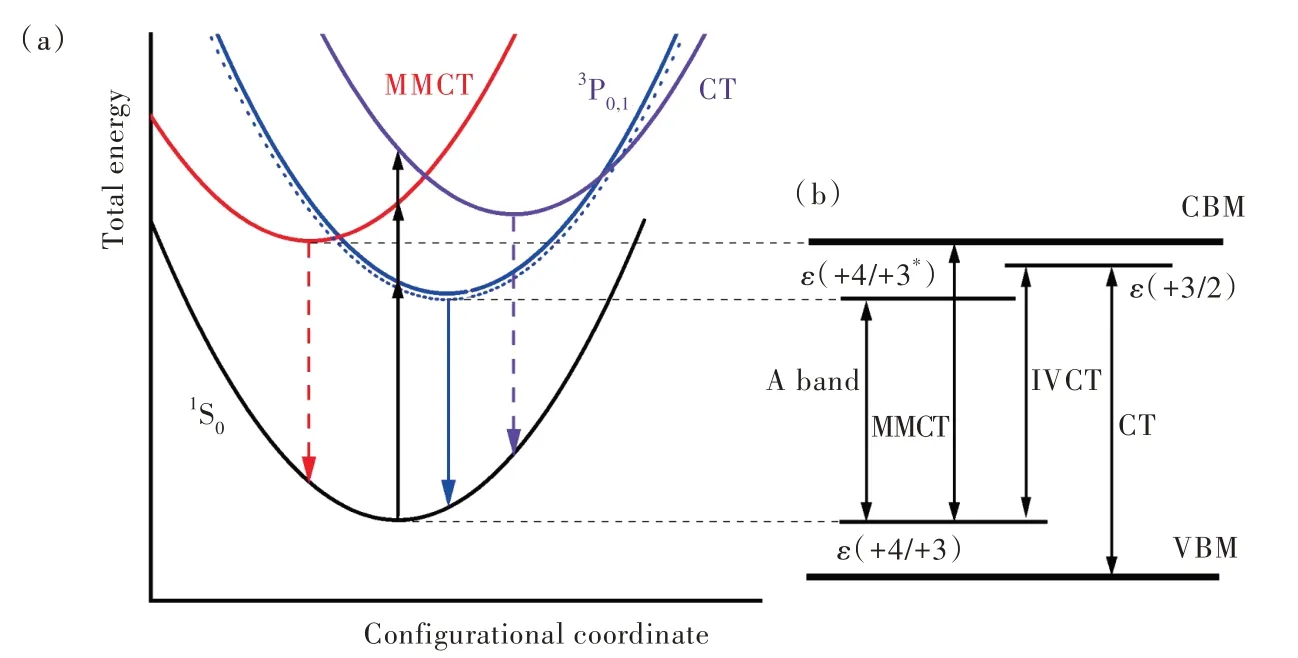
图1 （a）位形坐标图：黑线为竖直吸收，蓝线为最低3P0，1激发态的竖直发射，红虚线和紫虚线分别表示源自MMCT态和CT态的竖直发射（高激发态通常不提供发射，记作虚线）；（b）电荷转变能级图：黑色双向实线为各类跃迁（A带、MMCT、CT和IVCT）的零声子线。ϵ（+4/+3）和ϵ（+3/+2）分别为Bi3+离子扮演作空穴和电子陷阱的能级，其相对带边能隙则为陷阱深度。ϵ（+4/+3）和ϵ（+4/+3*）可看成Bi3+离子1S0和3P0，1态在带内的位置。Fig.1（a）The configuration coordinate diagram：the black and blue lines indicate the absorption and the emission transitions，and the red and purple dashed lines indicate the fictitious emission transitions from the MMCT and CT states，respectively.（b）The charge transition level diagram：the black bidirectional solid lines are zero phonon lines of various transitions（A band，MMCT，CT and IVCT），ϵ（+4/+3）andϵ（+3/+2）are the hole and electron trap levels provided by Bi3+ions，respectively.The hole and electron trap depths are given byϵ（+4/+3）minus VBM and CBM minusϵ（+3/+2），respectively.Whereasϵ（+4/+3）andϵ（+4/+3*）can be also regarded，correspondingly，as the locations of1S0 and3P0，1 states of the Bi3+ion in the band gap in the sense of adiabatic ionization.

具体到不同材料，Bi3+离子各激发态的相对位置可能存在较大差异。此外，高对称体系中Bi3+掺杂可能引起杂质激子态的发射，而非等价取代的Bi3+格位还存在电荷补偿缺陷的影响。对于Bi3+发光材料，指认其发射的激发态来源以及给出完整的发光过程一直是实验和理论研究共同面临的挑战。

3 各类光跃迁模拟

3.1 A带 跃 迁 和IVCT态 跃 迁

两电子图像的Seitz模型[33]被广泛接受并应用于当前Bi3+发光材料的机理解释。6s16p1激发组态在自旋轨道耦合及交换作用影响下的能级分裂如图2所示。基于该模型的拓展，人们进一步发展了分子轨道理论[34]和镶嵌团簇的从头计算[35]，并用于Bi3+离子6s16p1激发组态能级结构以及相关的光跃迁性质的定量计算。2014年，Du将杂化密度泛函方法应用于同样拥有6s2外壳层的Tl+离子掺杂材料[36]。虽然作为一种单电子计算方案，密度泛函计算不能完全再现所有多电子能级的能量，但其计算得到的基态1S0和最低激发态3P0,1的激发和发射能与实验结果较为吻合。

密度泛函理论是一种用于基态计算的单电子理论，但通过一些电子占据的限制方法，可以实现激发态的模拟，并给出激发态的平衡几何构型以及电子结构性质[37]。孤立Bi3+离子的激发态计算中，在考虑自旋轨道耦合的密度泛函计算中通过限制性占据方法，可以将一个电子从6s1/2的Kohn-Sham轨道移动并束缚到6p1/2轨道，以形成3P0,1激发态，再对该激发态进行相应的结构弛豫，实现激发态平衡构型的计算。对于电子从Bi3+离子到近邻Bi3+的电荷迁移态低于Bi3+离子自身3P0,1态的体系，通过限制性占据方法我们也可以实现IVCT激发态平衡几何构型的计算。值得注意的是，密度泛函方法中通过单电子轨道束缚占据方法模拟出的3P0,1激发态（见图2）是对最低发射能态的近似，并不能简单等同于Seitz模型中3P0和3P1能态中任何一个。在获取基态及激发态平衡构型的基础上，根据Franck-Condon原理，基态平衡构型下激发态和基态的总能差（ΔSCF方法[38]）对应到激发能，而激发态平衡构型下激发态和基态的总能差则为发射能。

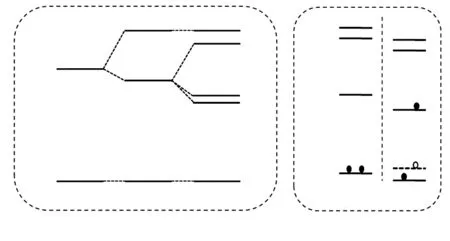
图2 Seitz模型描述的与密度泛函理论单电子轨道（KS orbitals）计算的最低激发态对比，自旋轨道耦合效应已被计入。Fig.2 Comparison between the lowest excited states described by the Seitz's multi-electron and single-electron Kohn-Sham（KS）orbital models of the density functional theory.The spin-orbit coupling has been considered.

3.2 CT和MMCT态 跃 迁

杂化泛函计算可以提供较为准确的能带结构计算，有望准确描述电荷迁移态跃迁（MMCT和CT态）。具体计算时，考虑到接近基质带边的束缚电子或空穴对发光中心的局域几何结构影响很小，可以通过在密度泛函计算中控制电子结构（体系电子数量），使之对应于Bi4+和Bi2+掺杂的体系，再进行结构弛豫得到近似的MMCT和CT态平衡几何构型。

MMCT激发态由Bi4+离子加一个被束缚在导带底的电子组成，故该激发态能量可通过Bi4+掺杂体系能量加上导带底的一个电子的能量来近似，而跃迁能则为激发态能量与同几何构型下的基态体系的能量之差，即：

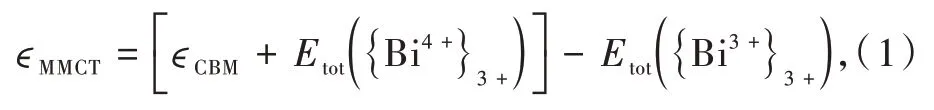
其中，两个“3+”下标表示基态几何结构的Bi4+掺杂或Bi3+掺杂体系总能，计算结果为MMCT跃迁的激发能，而对于发射能则需要在“4+”（Bi4+掺杂体系）平衡几何构型下进行初末态总能差的计算。类似地，也可以用Bi2+离子掺杂体系加一个被束缚在价带顶的空穴的总能量与基态体系之间的能量差，计算CT跃迁的吸收和发射能，即：

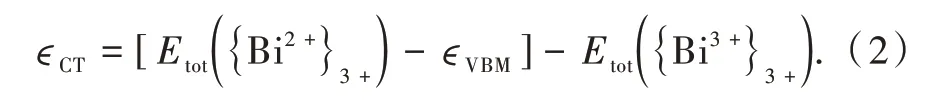
总的来说，Bi3+掺杂体系最低的激发态，即实验中发光占据主导的激发态通常容易计算获得，而更高的激发态或亚稳态则需要近似考虑。结合不同的发光中心局域结构以及该构型下的体系能量计算，可以绘制不同能态在不同构型下的势能面曲线，进而构建位形坐标图并分析完整的激发发射过程。这样计算的光跃迁能可以和实验观测到的光谱的最低激发发射能相比较。然而，一些体系中电荷迁移态的束缚电子（空穴）会对发光中心产生较大影响，在激发态结构和光跃迁能量计算中则需要具体分析。此外，第一性原理计算中存在和晶格尺寸相关的误差以及“带隙问题”[39-40]，这些都会对材料电子结构性质等相关方面的分析带来一定的影响，本文这里并不作深入的展开。

4 Bi3+掺杂体系的计算模拟结果分析

4.1 CaMO3∶Bi3+（M=Zr，Sn，Ti）

对于MMCT和A带两者之间的发射竞争，Boutinaud曾提及过三种可能的模型[12]，相应的情形在CaMO3Bi3+（M=Zr,Sn,Ti）体系中得到了很好的体现，相关工作[21]对该系列材料进行了第一性原理计算并给出了发光过程。实验观测到三类材料的发光现象存在明显差异，其中CaTiO3∶Bi3+[41]和CaSnO3∶Bi3+[42]的发射波包具有比CaZrO3∶Bi3+[43]更大的展宽，三者的半高全宽分别为0.57，0.59，0.31 eV。低温环境中，CaSnO3∶Bi3+除了峰值位于452 nm（2.74 eV）的主要发射外，还存在一个360 nm（3.44 eV）附近较弱的发射峰。三类材料的激发光谱均具有多个峰值，CaTiO3∶Bi3+的激发覆盖250～400 nm（3.10～4.96 eV）范围，峰值位于320 nm（3.88 eV）且在375 nm（3.31 eV）处呈现出一个肩峰，该体系测量的激发光谱于250 nm（4.96 eV）处在短波方向呈现被截断的情况。CaSnO3∶Bi3+主 要 在308 nm（4.02 eV）和260 nm（4.77 eV）附近有两个激发峰值。CaZrO3∶Bi3+的激发谱较为清晰，包含一个峰值处于304 nm（4.07 eV）的窄带激发（0.48 eV的半高全宽）和覆盖214～248 nm（5.0～5.8 eV）的宽带。

第一性原理计算实现了CaMO3∶Bi3+体系MMCT、A带和CT态的激发能计算，其数值能指认实验测量的激发光谱，系统解释了三种基质中Bi3+光谱现象的差异，从而较准确地揭示了发光机理。具体来说，计算给出的CaTiO3∶Bi3+的MMCT激发能为3.05 eV，A带激发较高为3.69 eV，CT激发能（4.72 eV）则远高于基质的带隙3.72 eV，分别对应于肩峰（3.31 eV）、激发宽包（峰值3.88 eV）和短波截断附近的激发（4.96 eV）。计算指出CaSnO3∶Bi3+体系带隙比CaTiO3的带隙大1.36 eV，而导带底的上移导致MMCT激发态的位置更为接近A带激发态，分别为3.78 eV和3.99 eV。由于两者的激发峰值接近，MMCT激发预计被偶极部分允许的较强A带激发光谱所掩盖，对应于实验上4.02 eV附近的激发单峰。CaZrO3∶Bi3+体系带隙最大（5.94 eV），因而MMCT激发远高于A带。计算的A带激发（4.10 eV）对应于测量的4.07 eV附近窄带激发，而CT（5.50 eV）和MMCT（5.19 eV）激发重叠形成实验所测到的宽带。

结 合 图3，我 们 对CaMO3∶Bi3+（M=Zr,Sn,Ti）的发射差异进行如下讨论。CaTiO3∶Bi3+体系的基质带隙较小，Bi离子的6p轨道位于导带深处，因而其发射源自于最低的MMCT激发态，从而波包展宽较大。CaSnO3的带隙比CaTiO3的带隙大1.36 eV，导带底的上移使得MMCT和A带激发态的相对位置有别于CaTiO3。室温下，该体系A带激发态上的电子会弛豫到最低的MMCT激发态并发射。而低温环境中，由于A带与MMCT激发态的发光中心局域环境存在较大的结构差异，CaSnO3∶Bi3+体 系 的 发 射 除 了 包 含MMCT发射，还可以观察到较弱的A带发射。CaZrO3基质的带隙更大，导带底的进一步抬升使得MMCT激发态远高于A带（3P0,1）激发态，因而发射转变为以A带为主。可见，构成导带底成分的阳离子性质的改变会引起导带底的移动，在很大程度上影响着Bi3+离子的6p轨道与CBM之间的相对位置，进而实现MMCT与A带发射的转变。这与Boutinaud提出的A带和MMCT态跃迁竞争图像一致。

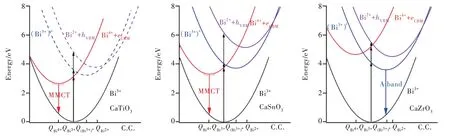
图3 CaMO3∶Bi3+（M=Ti，Sn，Zr）体系的位形坐标图。随着M离子变化，体系带隙增加，MMCT和3P0，1激发态之间的相对位置发生变化，进而使得体系发光性质改变。Fig.3 Configurational coordinate diagrams of the CaMO3∶Bi3+（M=Ti，Sn，Zr）.Along M=Ti，Sn，Zr，the band gap of the system increases，and the relative position between MMCT and3P0，1 excited state changes，which leads to the switch from MMCT emissions in the first two systems to A band emission in the third system.

4.2 MPO4∶Bi3+（M=Y，La）

前文提到，经验模型以及实验研究对MPO4∶Bi3+（M=Y,La）体系的光谱分析仍然存在一些困惑。基于YPO4∶Bi3+的实验测量，Blasse[44]报道了233 nm（5.32 eV）激发下寿命为0.7µs的342 nm（3.62 eV）发射，并将之指认为A带光跃迁。Jüstel等[45]则将报道的160 nm（7.75 eV）激发下波长为241 nm（5.14 eV）的发射指认为A带发射。Cavalli等[31]额外探测到长波发射具有227 nm（5.46 eV）的窄带激发和覆盖150～190 nm（6.53～8.27 eV）的激发，分别指认为A带和1S0→1P1的激发。Boutinaud[12]基于公式模型，判断YPO4∶Bi3+峰值位于5.32 eV的激发为MMCT，并与A带的激发能相近，3.62 eV附近的宽带发射则可能源自MMCT激发态。为了进一步确定长波发射的来源，Srivastava等[46]分析了YPO4∶Bi3+长波发射强度与掺杂浓度之间的依赖关系，指出该发射和Bi3+离子对及团聚有必然联系。Dorenbos[26]基于经验模型提供的指认有别于Boutinaud，他认为MMCT激发能为7.3 eV，6.53～8.27 eV的激发同时包含MMCT和1S0→1P1。

通过确定孤立Bi3+离子A带、MMCT、CT激发态以及Bi3+离子对（IVCT）激发态，Feng等通过第一性原理计算[23]明确了YPO4∶Bi3+体系的发射来源。其中，计算的A带发射能5.10 eV明显低于CT（5.66 eV）和MMCT（7.53 eV）的发射，可以很好地指认短波发射（5.14 eV）。长波发射则源自于Bi3+离子对激发态，其计算的IVCT发射能为4.22 eV，略高于实验测量值，偏差可归结为基于梯度密度近似泛函的计算中，未能充分考虑Bi3+离子对的激发态结构弛豫。计算的A带激发能为5.54 eV，与Cavalli等测量的激发光谱中5.46 eV的窄带激发相一致，进一步明确了YPO4∶Bi3+的A带跃迁性质。此外，计算指出MMCT、CT和1S0→1P1的激发分别在150，175，159 nm，均处于150～190 nm的激发宽包内，支撑了Dorenbos经验模型给出的结论。

对于LaPO4∶Bi3+体系，Blasse[47]报道实验测量的241 nm（5.14 eV）附近的窄带激发为A带，Moncorgé等对此进行了验证[48]，并指出该激发可以导致365～620 nm（2.00～3.40 eV）峰值 位于450 nm（2.76 eV）的发射。同时，241 nm还是产生450 nm发射的最低激发能。显然，该激发发射过程体现的Stokes位移过于反常，涉及复杂的发光过程。Boutinaud[12]的经验模型指出MMCT激发位于227～263 nm（4.71～5.46 eV），因而质疑5.14 eV附近的激发可能为MMCT且A带的吸收在更高的能量。Dorenbos[26]则参考YPO4∶Bi3+，指出175 nm（7.09 eV）附近的激发为MMCT。对于LaPO4∶Bi3+的发射能，考虑到Jahn-Teller效应参与的可能性，对于该发射到底为A带发射还是电荷迁移态发射，并未形成确定性的判断[15]。

Feng的 计 算 工 作[23]同 样 对LaPO4∶Bi3+的 光 跃迁进行了研究，其中，计算的A带激发能为5.23 eV，可以对5.14 eV附近的窄带激发进行确认。进一步计算指出，CT（6.23 eV）的激发远低于MMCT（8.23 eV）和1S0→1P1（7.35 eV）的激发能。可以尝试将实验中观察到的200 nm（6.23 eV）激发指认为CT，而160 nm（7.75 eV）左右的若干高激发峰指认为MMCT和1S0→1P1。虽然计算给出的CT发射能（3.74 eV）相较于实验测量显著偏大，但结合能级结构图像以及估计的A带发射能，Feng等倾向于认为，LaPO4∶Bi3+中的发射为CT发射。

位形坐标图（图4）展示了YPO4∶Bi3+的A带发射和LaPO4∶Bi3+的CT发射的发光过程。对于YPO4∶Bi3+，CT激 发 态 的Bi2++hVB势 能 面 与A带 激发态的（Bi3+）*势能面交错，前者很容易在声子协助下通过无辐射弛豫到后者，因而不会导致CT发射。MMCT激发态的Bi4++eCB势能面和（Bi3+）*势能面相交，同样会通过无辐射弛豫到后者。因而，YPO4∶Bi3+中的发光为最低的3P0,1激发态的A带发射。基于相同的分析，LaPO4∶Bi3+体系的发光则为Bi2++hVB激发态（CT）的发射。

图4 YPO4∶Bi3+（a）、LaPO4∶Bi3+（b）体系的位形坐标图，用于呈现在不同激发下分别导致A带和CT发射的激发、弛豫和发光过程。Fig.4 Configuration coordinate diagrams of YPO4∶Bi3+（a）and LaPO4∶Bi3+（b）systems.The difference in excitation and relaxation processes in the two systems leads to A band emission in YPO4∶Bi3+but CT emissions in LaPO4∶Bi3+.

4.3 GdAlO3∶Bi3+中的IVCT

IVCT作为电子在近邻Bi3+离子对之间的电荷迁移跃迁，在结构弛豫情况以及光跃迁Stokes位移大小方面与CT及MMCT跃迁非常接近。除去YPO4∶Bi3+体系中IVCT跃迁的计算，我们还围绕IVCT激发态的结构性质，对畸变钙钛矿GdAlO3∶Bi3+体系[22]中Bi3+离子对的发光机理进行了研究。GdAlO3∶Bi3+中近邻的Bi3+离子对（其中离子分别记作Bi1、Bi2）存在三种不同的可能类型。如图5所示，其基态结构中Bi1与Bi2之间的距离分别为0.372，0.378，0.384 nm，其中仅第二类Bi3+离子对的Bi1和Bi2互换时具有空间反演对称性。孤立Bi3+离子的局域环境相同且上述三类离子对的Bi离子间距差异较小，虽然Bi3+离子对激发态的性质存在差异，但三者的跃迁能和发光性质依旧较为相近。

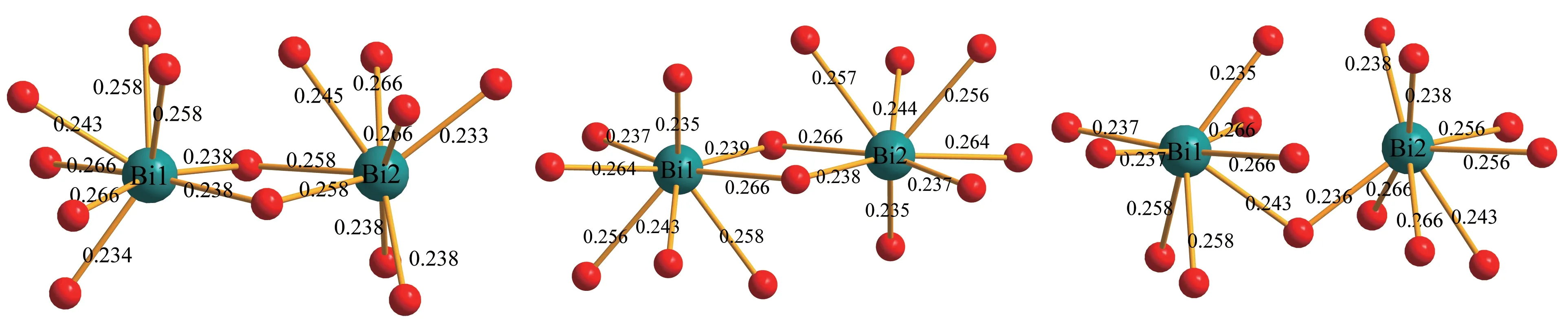
图5 GdAlO3∶Bi3+中Bi1与Bi2之间的距离分别为0.372，0.378，0.384 nm的三类近邻Bi3+离子对的局域环境。Fig.5 The local environment of three types of Bi3+pairs in GdAlO3∶Bi3+.The Bi1-Bi2 distances are 0.372，0.378，0.384 nm.

通过从不同初始结构出发进行结构弛豫，给出 了 三 类 近 邻Bi3+离 子 对 的（Bi12+-Bi24+）以 及（Bi14+-Bi22+）激发态，两者分别对应于电子从Bi1到Bi2以及Bi2到Bi1的电荷迁移。考虑到Bi2+的局域环境呈现扩张趋势，而Bi4+的局域环境呈现收缩趋势，（Bi12+-Bi24+）以及（Bi14+-Bi22+）激发态之间存在较大的构型差异。第一类Bi3+离子对的激发态（Bi12+-Bi24+）和（Bi14+-Bi22+）构型的Bi-Bi间距分别为0.362 nnm和0.391 nm,而第三类Bi3+离子对分别为0.391 nm和0.355 nm。由于第二类Bi3+离子对具备空间反演对称性，（Bi12+-Bi24+）和（Bi14+-Bi22+）激发态的性质相同。此外，在该类型离子对的计算中，还获得了体系的亚稳激发态（Bi3+-Bi3+）*。计算给出了（Bi2+-Bi4+）类型的GdAlO3∶Bi3+体系中基态和激发态的电荷密度图（图6），清楚地展示了Bi1到Bi2的电荷转移。同时，计算得到的Bi2+-Bi4+类型激发态的发射能与实验光谱测量的情况相一致。

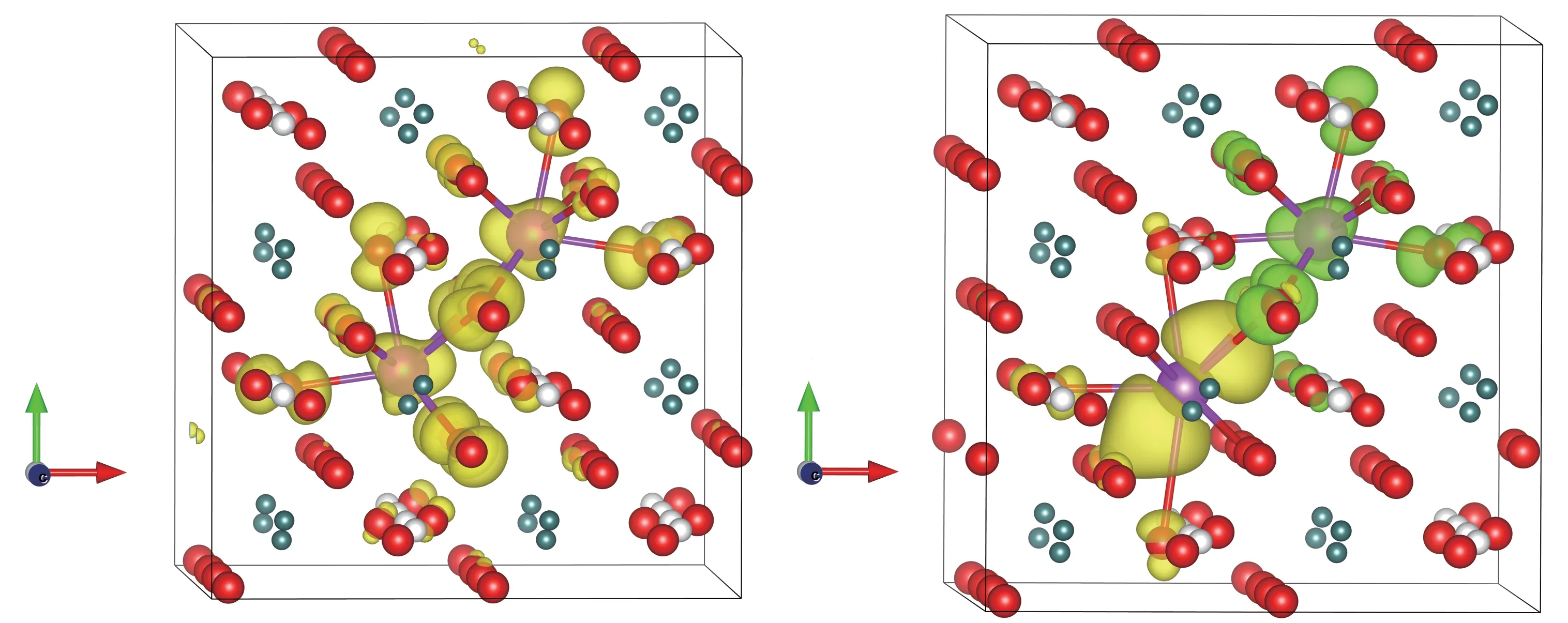
图6 GdAlO3中Bi3+离子对的电荷密度示意图：（a）基态（Bi3+-Bi3+）的6s轨道电子；（b）（Bi2+-Bi4+）激发态中Bi2+离子6p轨道电子（黄色）和Bi4+离子6s轨道空穴（绿色）。Fig.6 The charge-density contours of the Bi3+pair in GdAlO3：（a）the electron of 6s orbital of the（Bi3+-Bi3+）ground state，（b）the electron of 6p orbital（yellow）and 6s orbital（green）of Bi3+pair of the（Bi2+-Bi4+）excited state.

值得注意的是，计算结果表明GdAlO3中Bi3+离子对相对于两个孤立的Bi3+离子的结合能几乎为零，从而无明显的形成离子对的倾向，该结论符合最近邻间距0.35 nm以上的等价态替换的Bi离子对相互作用较弱的经验判断。此外，结构类似的YAlO3∶Bi3+体系并没有IVCT发射。结合Setlur等[49]对（Y,Gd）3（Al,Ga）5O12∶Bi3+体系的机理解释，计算指出GdAlO3∶Bi3+中独特的Bi3+离子对发光与激发光通过Gd3+离子网格间能量传递导致的对基质中自然分布导致的少量Bi3+离子对的敏化有关。在GdAlO3中，Gd3+离子的8S7/2→6P7/2跃迁与孤立Bi3+的A带发射能量相近。Gd3+离子的f-f轨道间的跃迁禁戒特性使得Gd3+的上激发态显示足够长的寿命且没有明显多声子弛豫过程。基质中大量的Gd3+离子形成了激发能迁移的通道，从而把激发Bi3+离子的能量通过Gd3+迁移到Bi3+离子对，使后者处于Bi2+-Bi4+激发态，最终导致和激发能有显著红移的发射。整个激发、能量传递和发射过程如图7所示。

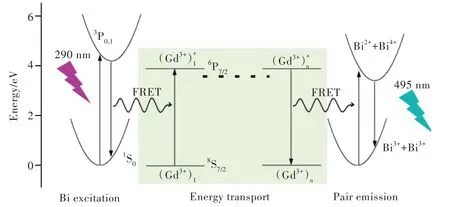
图7 GdAlO3∶Bi3+体系中Gd3+作为能量传递的桥梁，将孤立Bi3+离子3P0，1激发态能量传递到Bi3+离子对（Bi2+-Bi4+）激发态并引起离子对发射机理示意图。Fig.7 Photoluminescent mechanism of Bi3+pair in GdAlO3∶Bi3+，where Gd3+ions form an energy migration network to connect excited Bi3+ions with a Bi3+pair to promote the latter to the Bi2+-Bi4+type excited state，from which the emission is produced.

除了上述氧化物体系之外，Liu等[25]通过第一性原理计算研究了Bi3+掺杂的卤化物双钙钛矿体系，包括Cs2AgInCl6、Cs2NaLaCl6和Cs2NaYCl6等，揭示了卤化物体系中自陷激子猝灭Bi3+激发态的过程。例如，在Cs2AgInCl6体系中，In3+离子上的束缚电子和Ag+离子上的束缚空穴组合形成的自陷激子激发态能量远低于Bi3+掺杂离子的3P0,1激发态。因而，Cs2AgInCl6∶Bi3+的3P0,1激发态 会弛豫到 能量较低的自陷激子态进行发光，使得Bi3+激发态发光 猝 灭。在KCl∶Bi3+和Cs2SnCl6∶Bi3+体 系 的 研 究中，Liu等还探讨了非等价取代时，电荷补偿引入的近邻本征缺陷对Bi3+发光过程带来的影响。Chen等 通 过 对MXCl3∶Bi（M=K,Rb,Cs;X=Mg,Cd）[50]和M2B5O9Cl∶Bi（M=Ba,Sr,Ca）[51]体系的计算和分析，展示了基于密度泛函理论的第一性原理计算在低价态Bi离子发光模拟中的可行性。Qiao等[52]结合本征缺陷的形成能和陷阱深度计算，研究了长余辉体系LiREGeO4∶Bi3+（RE=Y,Sc,Lu）中发光中心通过复合电子产生紫外长余辉的机理。由此可见，第一性原理计算已经充分展示了其在铋离子掺杂发光材料的光谱指认及发光机理解释方面的重要作用。

5 对Bi3+离子发光构效关系的讨论

第四节中所介绍的计算普遍通过获取明确的基态激发态性质以及各类光跃迁能量，构建完整的位形坐标图，进而对实验光谱进行分析指认。实际上，基于发光中心的配位环境、基质带隙、缺陷能级等，同样也可以简易实现Bi3+离子掺杂体系的光谱分析和发光预测。

图8总结了计算研究中揭示的具备显著A带、MMCT或CT发射体系，包括基质带隙以及电荷转变能级在禁带中的位置。A带占据主导的体系中，6s与6p轨道电子对应的电荷转变能级均位于禁带中且离价带和导带较远。换言之，可以提供A带发射的Bi3+掺杂离子也是稳定的电子和空穴俘获中心。这一结论支撑了Dorenbos的结论[26]。在电荷迁移态跃迁主导体系的能级图像中，Bi3+离 子 在CaTiO3、LuVO4等 体 系 中 仅 可 以 提供稳定的空穴陷阱，发光中心可以通过俘获空穴形成稳定的Bi4+离子同时无法进一步俘获电子形成3P0,1激发态，因而其发射源自于MMCT激发态。类似地，在LaAlO3及LaPO4中Bi3+仅可以提供稳定的电子陷阱，其发射通过Bi2+离子与价带空穴复合产生，即CT发射。

此外，图8中呈现的Bi3+空穴陷阱深度展示出一定的随价带起伏的特征，而电子陷阱和导带底之间的距离则缺乏类似趋势。这和Bi3+的6s以及6p轨道特性相关，Bi3+离子的6s轨道为发光中心与配体之间杂化形成的反键轨道，6s成分相对小，且通常靠近价带顶。同时，Bi3+离子的空穴陷阱深度主要由6s轨道与配体轨道之间的杂化程度，即电子云重排效应决定，因而可以参考经验模型[26]中影响电子云重排效应的因素进行初步预测。在一系列氧化物钙钛矿体系中，空穴陷阱深度与近邻配体的键长呈线性负相关，见图9。然而，卤化物钙钛矿中的Bi3+空穴陷阱的性质与氧化物体系存在显著差异（数据未展示），有待进一步探索。结合该图像可知，在LaAlO3∶Bi3+和LaPO4∶Bi3+中，Bi3+离子取代的La3+格位具有相对较为宽松的局域环境，6s轨道难以形成稳定的空穴陷阱，使得这两个体系中发光呈现为CT类型的发射。另一方面，6p轨道则由Bi3+离子主导，与导带底之间的距离因基质不同会存在较大差异，明确相应的能隙需要诉诸于第一性原理计算。

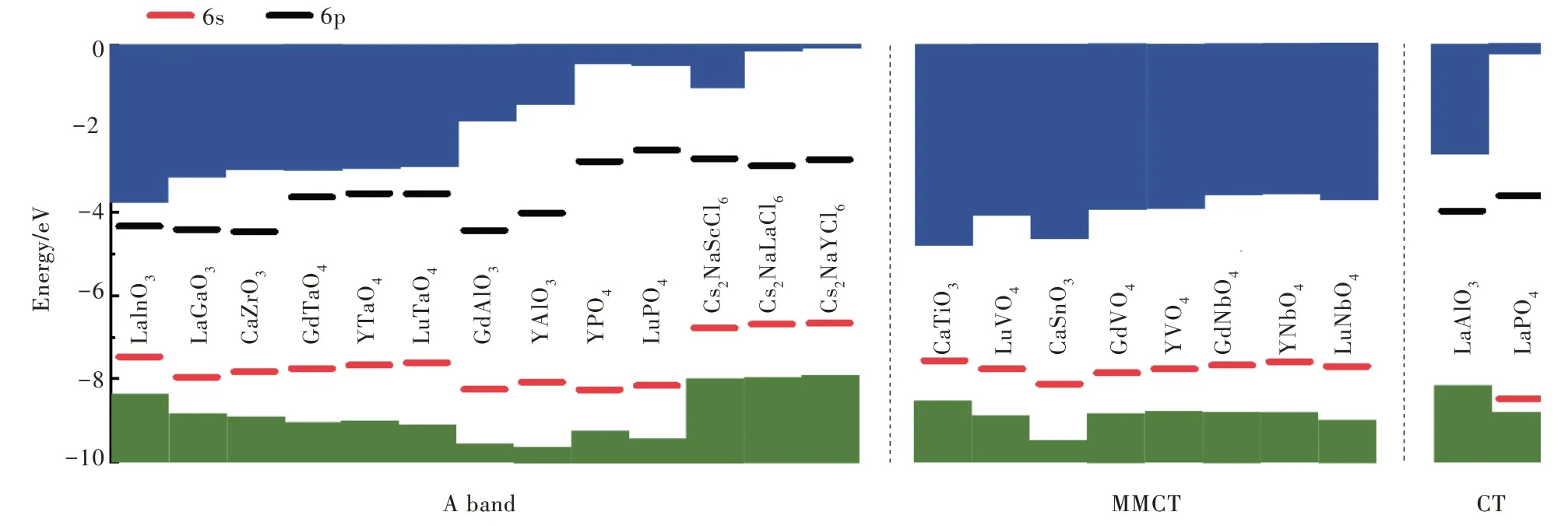
图8 实验中存在显著A带、MMCT和CT发射的Bi3+掺杂体系的电荷转变能级图像，其中各体系的价带顶相对真空位置对齐，6s和6p分别为Bi3+离子扮演的电子和空穴陷阱能级，而6s和6p相对带边的能隙则分别为空穴和电子陷阱深度[21-25］。Fig.8 The charge transition level diagrams of Bi3+doped systems that produce dominantly A band，MMCT or CT emission as confirmed by experiments.Wherein the VBMs are determined by their vacuum referred binding energies，6s and 6p are the electron and hole trap states provided by Bi3+in the hosts.The relative energies of 6s to VBM and CBM to 6p give the trap depths[21-25］.

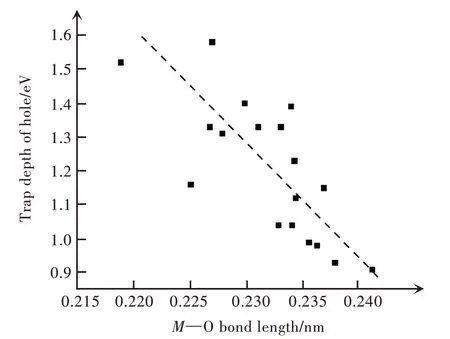
图9 一系列氧化物中计算所获得的空穴陷阱深度与基质中被取代阳离子到最近邻氧配体距离之间的关联Fig.9 Calculated hole trap depth versus the original M—O bond length in the host，where M is the cation site replaced by Bi.

6 结论与展望

Bi3+离子的能级结构和跃迁过程可以通过实验上不同基质的选择进行调节，因而不同材料中的Bi3+发光性质存在较大差异，发光波长可以涵盖紫外到近红外区域。通过理论计算分析Bi3+掺杂材料的发光机理能够支撑相应的实验研究，促进和实现对新型Bi3+掺杂发光材料的设计和性能改进。基于密度泛函方法的第一性原理计算可以有效地实现不同基质材料中多价态Bi离子的基态和激发态几何与电子结构性质的计算以及相应发光动力学过程的模拟，进而解决Bi3+掺杂发光材料发射的跃迁指认问题。此外，发光中心局域结构、基质带隙、缺陷能级等与Bi3+离子发光性质之间的联系也可以被简单预测。

当前的第一性原理计算研究已经可以处理常规的Bi3+离子掺杂发光材料，其计算的跃迁能与实验测量结果的符合度较好，同时也初步建立了发光性质随基质带隙大小、局域结构环境、缺陷能级等变化的规律。然而，仍有许多与Bi3+离子发光相关的科学问题有待解决：（1）Bi3+掺杂体系的长余辉过程：长余辉材料的发光中心通过俘获储能缺陷释放的载流子（电子或空穴），可以在移除激发光源后仍旧提供长时间的发光。固体中的Bi3+离子既可以作为储能陷阱，也可以作为发光中心。当Bi3+离子作为发光中心时，其长余辉发光可以通过俘获电子、俘获空穴或俘获电子-空穴对三种方式实现，而完全理解这样丰富的长余辉发光过程则需要理论计算的协同。此外，对于源自Bi3+离子对激发态或复合发光中心的长余辉发光，其发光过程则更加复杂，发光机理的揭示更需要理论计算的帮助。（2）Bi3+离子的反常红移发射:Bi3+离子掺杂体系通常为可见光发射，然而，在一些材料中可以出现明显红移的发光，例如M2O3∶Bi3+（M=Y,Lu,Gd）则存在两套激发发射光谱，且其中一套光谱的Stokes位移异常偏大。该反常红移的发射有电荷迁移态跃迁或配位场影响下的A带发射两种解释。通常认为固体中Bi3+离子的能级分裂主要受自旋轨道耦合影响，交换作用相对较弱，同时可以忽略配位场的影响。然而，当前的计算方案尚且缺乏量化分析配位场的能力，Ning等[53]在工作中采用多组态从头计算讨论了晶体场影响下的ALuGeO4∶Bi3+（A=Li,Na）的能级分裂，有望进一步发展计算方案并澄清M2O3∶Bi3+体系的发光机理。（3）Bi3+离子团聚机理：在许多体系中实验验证了Bi3+离子对发光的存在，包括本文提及的GdAlO3和YPO4体系。通过第一性原理计算可以获取Bi3+离子对激发态及与其相关的一些性质，但是大多数密度泛函的形成能计算并没有考虑温度效应，这导致在许多具有Bi3+离子对发射的体系中，其计算结果通常没有展现出团聚的倾向，从而并不能从几何结构层面支持Bi3+离子对的形成。特别是在GdAlO3∶Bi3+体系，我们已通过Gd3+能量传递过程进行了离子对发光机理的解释，但同样无法完全排除GdAlO3体系相较于YAlO3体系更容易形成Bi3+离子对或团聚的可能。因而，聚焦Bi3+离子团聚机理，在几何结构的理论研究中，考虑形成焓的温度依赖和形成熵的贡献将是我们不得不面对的难点与挑战。

本文专家审稿意见及作者回复内容的下载地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220245.