Crystal-field Splitting in Regular Polyhedron

SONG Zhen，LIU Quan-lin

（Beijing Key Laboratory for New Energy Materials and Technologies，School of Materials Science and Engineering，University of Science and Technology Beijing，Beijing 100083，China）*Corresponding Authors，E-mail：zsong@ustb.edu.cn；qlliu@ustb.edu.cn

Abstract：Crystal-field theory plays a fundamental role in understanding the energy levels of rare-earth and transition-metal elements in inorganic hosts.It has been fully developed for the octahedral field，both in analytical energy level expression and pictorial understanding.Nevertheless，the crystal field theory for other regular cubic polyhedra，including tetrahedron，cube and cuboctahedron，needs further investigation to show the similarities and differences with the octahedral field.In this work，the detailed crystal-field analysis of one d electron in those regular polyhedra is presented using the perturbation method.The exact crystal-field potentials are derived based on geometrical models with equivalent center-ligand bond length.The secular matrices are constructed and diagonalized to give the split energy levels.The crystal-field splittings for regular tetrahedron，octahedron，cube and cuboctahedron are calculated to be 40Dq/9，90Dq/9，80Dq/9 and 45Dq/9.In the end，the relative orientations between eg/t2g orbitals and the ligands are visualized to present a vivid understanding of the magnitude reverse.

Key words：crystal field；energy level；splitting；polyhedron

1 Introduction

Research on luminescent materials has greatly promoted the development of optoelectronic devices in recent years[1-3].Rare-earth or transition metal elements doped phosphors contribute a major part in solid-state lighting.Spectroscopic modulation has been widely investigated for those phosphors to meet the application requirements,such as adding redlight component to improve the lighting quality[4-5].Generally,the luminescence tuning is implemented by host structure variation through composition substitution[6].The guideline is derived from crystalfield theory,which describes the Stark effect of outer-shell valence electrons embedded in the electrostatic potential field originating from the neighboring anionic ligands.The crystal-field effect of one d electron embedded in 6-coordinated octahedron with point symmetry Ohhas been thoroughly investigated,from which a general rule about the bond length and the energy level splitting is derived to relate the spectroscopy with structure variation[7].It reflects the reciprocal relationship between 5th-power of bond length and the magnitude of the crystal-field splitting[8-9].Although there exist several exceptions,this rule has been widely applied in understanding the structureproperty relationship in luminescent materials.

The simple 5th-power rule is derived for the 6-coordinated octahedron,which bears point symmetry Oh.There also exist some other regular polyhedra belonging to the same symmetry,i.e.,4-coordinated tetrahedron[10],8-coordinated cube[11]and 12-coordinated cuboctahedron[12].Meanwhile,those polyhedra are suitable for luminescent dopant ions to reside in.For example,transition-metal ions prefer the smaller tetrahedron and octahedron,whereas rare-earth elements are usually found in larger cube or cuboctahedron[13-14].The crystal-field effects in all those regular cubic polyhedra share the same 5th-power reciprocal rule but differ in the splitting magnitude[15].In addition,the split energy levels are sorted reversely among those polyhedra.For example,the splitting of one d electron in the 6-coordinated octahedron has two high-lying egorbitals（dx2-y2,dz2）and three low-lying t2gorbitals（dxy,dyz,dxz）due to crystal-field splitting,which could be described pictorially from the arrangements of orbital lobes towards ligand anions[16].Meanwhile,the sorting of egand t2gorbitals are reversed in the 8-coordinated cube potential,together with a shrinkage in the energy-level difference.For tetrahedron and cuboctahedron,the investigations on crystal-field splitting magnitude and relative order of energy levels are less reported,and until now the pictorial description of orbital arrangements regarding ligands is still unclear as far as we know.

Analysis on luminescence tuning often relies on the understanding of crystal-field splitting in those regular polyhedra.For example,the photoluminescent excitation spectra of Ce3+in 8-coordination environment reveal two peaks near the low-energy side,which correspond to the two low-lying egorbitals[17-18].In multi-site structure such as garnet[19-20],spinel and pyrochlore[21-22],researchers need to compare the crystal-field strength of different coordination polyhedra to identify the cationic site-occupancy.Therefore,in this work we provide a detailed analysis of crystalfield effects of d1electron in regular cubic polyhedra using perturbation theory.The magnitudes of crystalfield splitting are given,together with the sorting order of the energy levels,and the orbitals are visualized together with the ligands.We hope this work could clarify the misconceptions and serve as a reference for chemists,physicists,spectroscopists and material scientists in the field of luminescent materials.

2 Methods

2.1 Geometrical Models of Regular Cubic Polyhedron

We set up the models of 4 types of regular cubic polyhedra,i.e.,tetrahedron,octahedron,cube,and cuboctahedron.Their centers are set as the origin of the Cartesian coordinate system,which is reserved to accommodate the dopant luminescent ion.The ligand coordinates of all the polyhedra are{（a,-a,-a）,（-a,a,-a）,（a,a,a）,（-a,-a,a）}for tetrahedron,{（a,0,0）,（-a,0,0）,（0,a,0）,（0,-a,0）,（0,0,a）,（0,0,-a）}for octahedron,（{a,a,a）,（a,-a,a）,（-a,a,a）,（-a,-a,a）,（a,a,-a）,（a,-a,-a）,（-a,a,-a）,（-a,-a,-a）}for cube,（{a,0,a）,（0,a,a）,（a,a,0）,（0,-a,a）,（a,-a,0）,（-a,0,a）,（-a,a,0）,（-a,-a,0）,（a,0,-a）,（0,a,-a）,（0,-a,-a）,（-a,0,-a）}for cuboctahedron.Those ligand coordinates are set to ensure that all the polyhedra share the same centervertex length a.The aim is to investigate the effect of coordination number on the splitting magnitude at the same bond length.

2.2 Expressing Crystal-field Potentials

Although all the regular cubic polyhedra belong to point symmetry Oh,their corresponding crystalfield potentials differ in algebraic expression.Let the ligand has charge Ze,then the electrostatic potential between the electron and the ligand is V=It could be further rewritten with the help of Legendre polynomials Pl（cosθ′）as

in which l is no larger than 4 for d electron and R=is the distance between the origin and electron with coordinates（x,y,z）.Every ligand has a potential calculated by its own coordinates,and the sum of all the ligand potentials is the crystal-field potential.The final expression could be simplified by selecting

this assignation was first introduced for the crystalfield splitting in octahedron[7],and also serves as the origin of 5th-power relationship.In this work,the definition of D is preserved for all the regular polyhedra.The expressions of crystal-field potential are listed in Tab.1

Tab.1 Crystal-field potential expressed by electron coordinates（x，y，z）

2.3 Construction of Perturbation Secular Matrix

The crystal-field splitting is caused by the Stark effect of the ligands.The changes in energy levels could be evaluated by the first-order perturbation energyby means of the d electron wavefunctionΨnlm=Rnl(r)Yml(θ,ϕ),in which Rnlis the radial part,Ymlthe angular part represented by the spherical harmonics.The wavefunctions of d electron with l=2 and ml=2,1,0,-1,-2 are 5-fold degenerated before applying the crystal-field potential perturbation,therefore the perturbation matrix with a total of 25 elements needs pre-evaluation before diagonalization.The matrix element could be expanded as

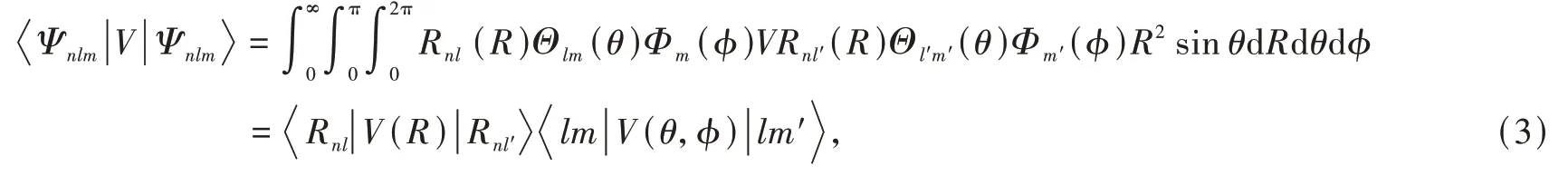
in which the angular part could be integrated but the radial part needs parametric substitution of

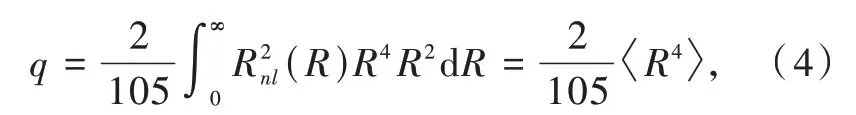
the residual R2in the integral is used for normalization of Rnl.Now we have the full expression of Dq,which is

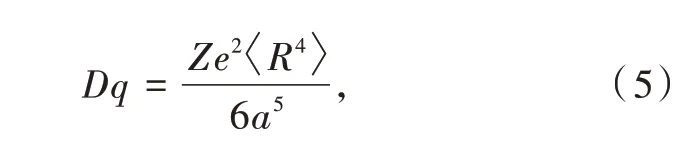
it has the energy scale,usually in wavenumber.Finally,the secular matrix could be expressed only by the product of two parameters Dq,as listed in Tab.2.Diagonalization of those matrices provides eigenvalues and eigenfunctions in Tab.3.It should be noted that all the regular polyhedra share the same Dq,because they are modelled with the equivalent centervertex length a.As a result,those crystal-field splittings are comparable.

Tab.2 Perturbation seculiar matrix constructed by eigenfunctions of d electron

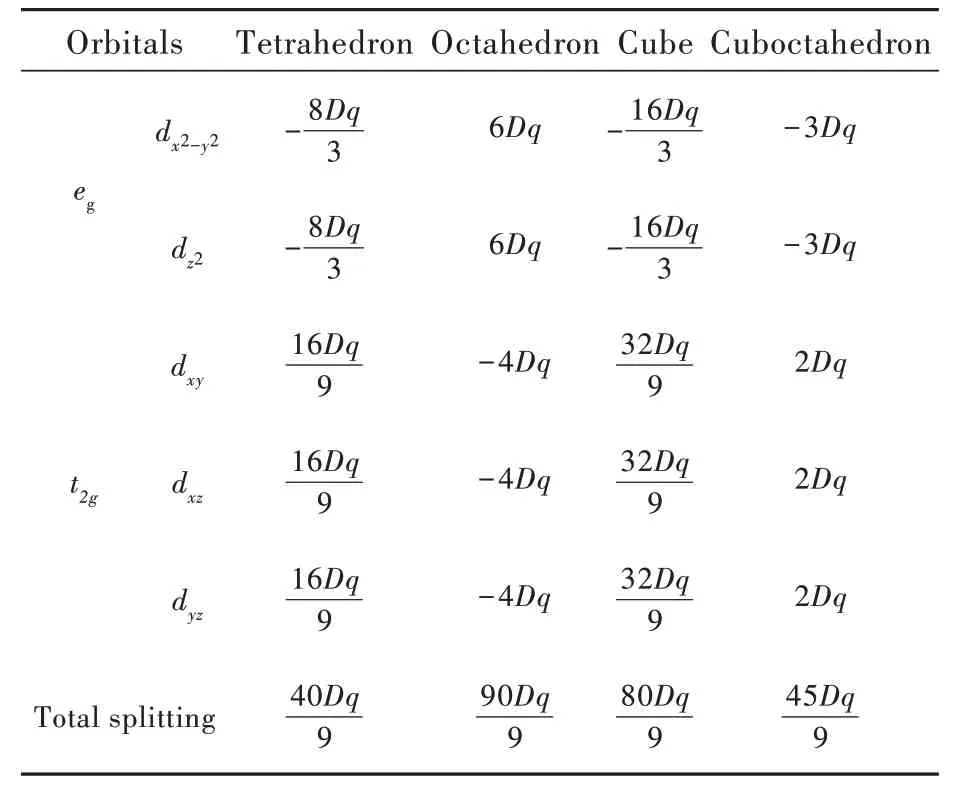
Tab.3 Diagonalization results of the seculiar matrix and the total crystal-field splitting

3 Results and Discussion

The results in Tab.3 are visualized in Fig.1,denoting the perturbed energy levels of egand t2gorbitals with regard to the unperturbed one with 5-fold degeneration.They are presented in the sequence of largr polyhedral coordination number.Since the point symmetries of all the polyhedra belong to the point symmetry Oh,it is expected from group theory that the 5-degenerated levels of d1electron will be split into egand t2gorbitals with 2 and 3 degeneration,respectively,i.e.,D(2)=eg⊕t2g.This scheme is confirmed in Fig.1.Solving the perturbation matrix further gives the quantities of both crystal-field levels,and their values differ in magnitude.In general,the total crystal-field splitting is decreasing as the polyhedron has more coordination number,except tetrahedron which has the smallest one.Octahedron has the largest 10Dq with the egorbital positioned higher than the t2gone,whereas all the other polyhedra have the opposite energy level sequence.For tetrahedron,the crystal-field splitting is 4/9 of that in octahedron,which is consistence with previous reports[23-24].Nevertheless,the magnitude ratio of the split energy levels keeps 2∶3.There also exist duple relationships among the crystal-field splittings of tetrahedron/cubeand cuboctahedron/octahedronIt is a coincidence that the coordination number is doubled and half reduced in both cases.

Fig.1 Crystal-field splitting of d1 electron in various polyhedral potentials.The dashed line represents the 5-fold unsplit energy levels.

The eigenfunctions could also be obtained by matrix diagonalization,and they are linearly combined into the d-electron orbitals and visualized in the frame of polyhedral ligands as shown in Fig.2-Fig.5.As the well-known energy level sequence in octahedron suggests（Fig.3）,those orbitals with lobes directed away from the ligand are positioned lower in the energy scale.For tetrahedron in Fig.2,the lobes of t2gorbitals are positioned near the ligands,whereas those of egorbitals are directed towards the gap between two adjacent ligands.Therefore,tetrahedron has low-lying eg orbitals.For cube in Fig.4,the t2g orbitals are also pointed towards the gap,but the eg orbitals have lobes directed into the virtual void surrounded by four neighboring ligands,which induces less electrostatic interaction with the ligand anions.Meanwhile,this kind of virtual void also explains the low-lying eg orbitals in cuboctahedron（Fig.5）,of which the high-lying t2g orbitals have lobes directed towards the ligand anion.

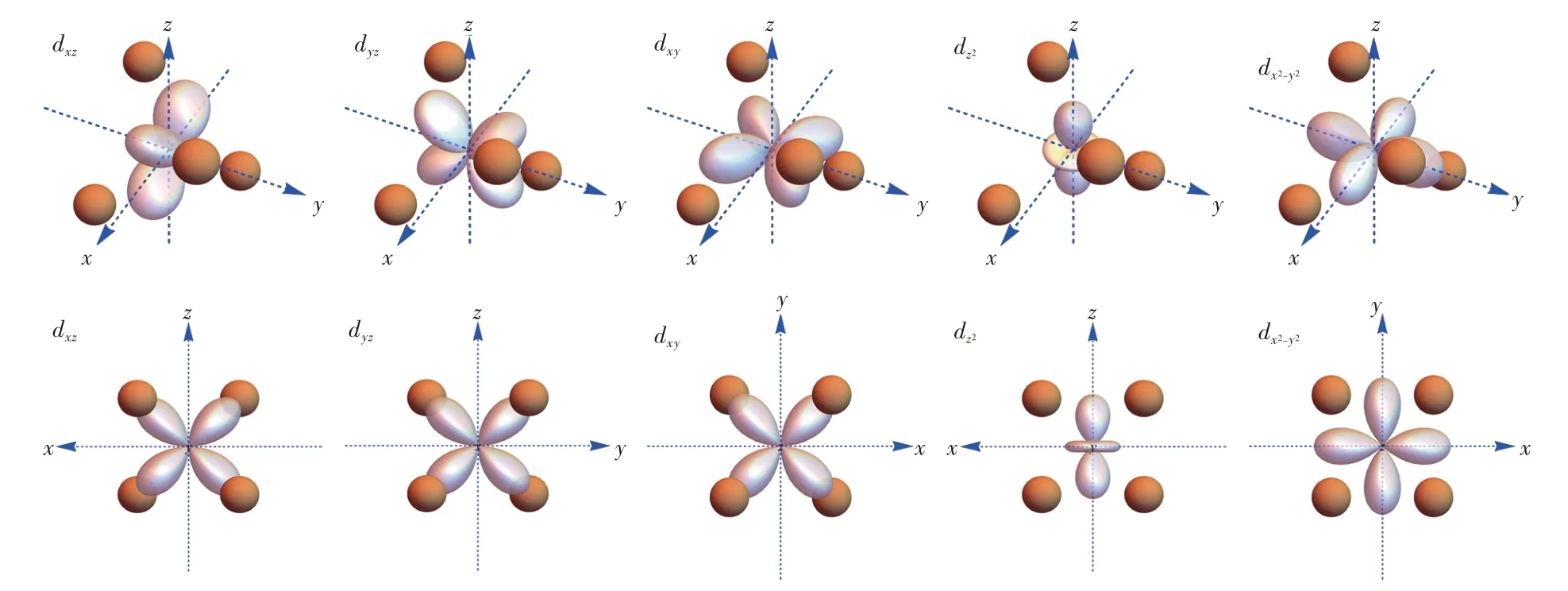
Fig.2 Visualization of d-electron orbitals in the frame of tetrahedral ligands.Up：stereo views.Down：views along[010］，[100］，[001］，[010］and[001］directions，respectively.

Fig.3 Visualization of d-electron orbitals in the frame of octahedral ligands.Up：stereo views.Down：views along[010］，[100］，[001］，[010］and[001］directions，respectively.

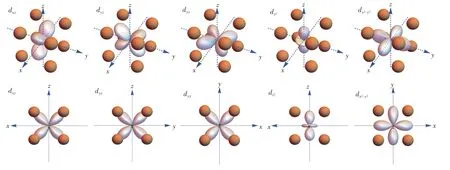
Fig.4 Visualization of d-electron orbitals in the frame of cube ligands.Up：stereo views.Down：views along[010］，[100］，[001］，[010］and[001］directions，respectively.

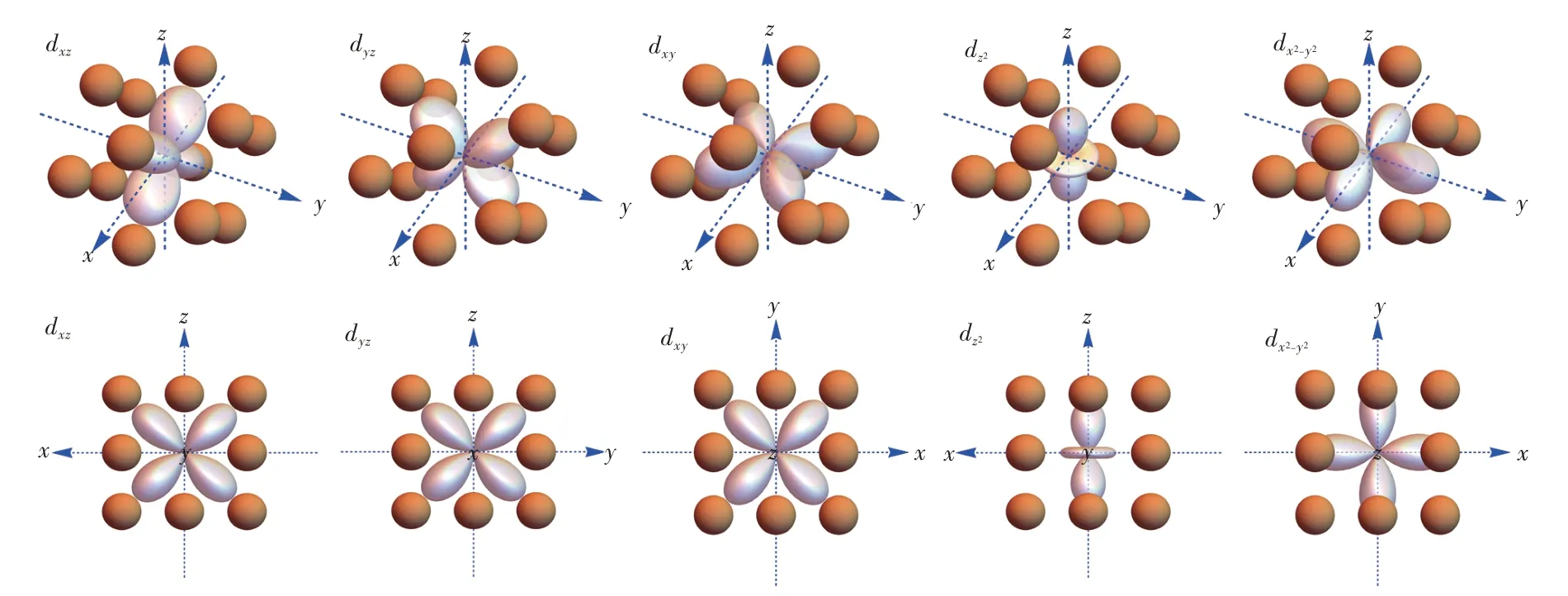
Fig.5 Visualization of d-electron orbitals in the frame of cuboctahedral ligands.Up：stereo views.Down：views along[010］，[100］，[001］，[010］and[001］directions，respectively.

4 Conclusion

In this work,the crystal-field effects in regular cubic polyhedra are analyzed in detail.The geometrical models are set up with equi-distant ligand for every polyhedron.Through perturbation theory,the total crystal-field splittings are expressed analytically asfor tetrahedron,octahedron,cube and cuboctahedron,respectively.The magnitude shows a descending trend with coordination number except tetrahedron.Meanwhile,there exist duple relationships between those splittings.Only octahedron has high-lying egand low-lying t2gorbitals,whereas the other polyhedra have the opposite sorting sequence.For pictorial understanding,the d electron orbitals are visualized together with the polyhedral ligands.It is found that those orbitals with lobes directed towards 4-ligand void or 2-ligand gap have lower energy by avoiding electrostatic repulsion.This work provides a deeper understanding of the crystal-field theory of regular cubic polyhedra.

Response Letter is available for this paper at:http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220190.