节点参数含应变的空间几何非线性样条梁单元*
2022-10-12卓英鹏齐朝晖
卓英鹏,王 刚,齐朝晖,张 健
(1.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023;2.大连理工大学 海洋科学与技术学院,辽宁 盘锦 124221)
引 言
实际应用中许多结构都可以采用梁的理论分析,例如大型可展开天线、柔性机械臂、涡轮螺旋桨等.但是随着材料的轻质化以及结构细长的特点,它们在工作过程中往往会产生很大的挠度.因此,如何构造出一种简洁高效的空间几何非线性梁单元是很多领域的共同需要[1-5].
当梁的截面发生大范围的刚体运动时,小变形理论中的线性应变不再适用,很多专家学者将Green 应变中的高阶项考虑进来以便描述几何非线性效应,即早期常用的基于Langrange 坐标系的TL 和UL 列式法,但是在推导过程中十分繁琐,且在分析计算过程中,经常忽略变形后的坐标转换矩阵,导致在大转角问题分析中无法收敛甚至出错[6-8].这就引发了一个问题:如何可以在利用现有成熟的线性单元基础上,采用一种更加简洁形象的策略来描述梁在大变形过程中截面的刚体运动?因此,Wempner[9]和Belytschko 等[10]最早提出了共旋坐标法,其主要思想是将单元的位移场分解为随单元坐标系的刚体运动以及相对于单元的小位移,即将构件的位形认为是单元坐标系的大范围运动与相对于该坐标系变形的叠加,这类单元在具体应用中展现出了明显的优势,在此基础上结合子结构法的使用和线性系统自由度凝聚理论,解决了实际工程中的很多问题[11-13],但是这种策略未考虑单元水平上的几何非线性问题,用于高速轻质系统的分析时经常遇到诸如动力刚化项遗失[14-15]、数值不稳定等问题.因此,如何构造一种几何非线性单元愈发值得重视.
针对几何非线性单元,Simo 等提出了一种精确几何模型方法[16-17],依据有限转动理论导出了具有客观性的应变度量,彻底摒弃了小位移小转动的线性梁理论,在处理几何非线性梁问题时具有较好的计算效率和精度[18-20];Romero 等[21]和Crisfield 等[22]以形心平移和截面转动参数作为节点坐标,对转动插值进行研究,转动和位移插值的独立性引起了诸如运动学描述冗余和剪切闭锁等困难;因此Zupan 和Saje 等[23-25]放弃了对转动参数的插值,以应变矢量作为节点坐标,对拉伸应变和弯曲应变进行独立插值;上述非线性单元均为Timoshenko 梁,解决细长结构时没有体现Euler-Bernoulli 梁的变形耦合关系.Shabana 提出了一种绝对节点坐标法,将单元节点的坐标定义在全局坐标系下,采用斜率矢量代替传统有限元中的节点转角坐标,可以避免转角插值,推导的多体系统微分-代数方程具有常质量阵、不存在科氏力和离心力项等特点[26-27],尤其是近几年,迅速地得到了广泛的应用,很多基于绝对节点坐标的梁、板、壳单元应运而生,这种单元虽然比传统有限元有优势[28-30],但其节点参数较多,无疑对计算效率会有影响.
此外,成熟的有限单元建模理论大都仍采用位移元进行离散[31],即直接选择节点位移和转角作为描述参数,这种以虚功原理为基础的位移元可以保证单元间位移的连续,一般应力对应于位移的二阶项,理论上,位移元建模单元间的应力仍然处于不连续状态,端部施加外力时,力的边界条件近似满足,这些情况只能通过不断缩小单元长度逐渐逼近连续和降低近似.大变形梁刚性截面在做大范围刚体运动时,传统位移元的应力不连续性以及力的边界条件近似性可能会在单元数量选择不合适的情况下降低分析精度.
因此,一个值得研究的问题是,是否可以构造一种几何非线性梁单元使其同时满足以下几个条件:①避免形心位移和转角独立插值造成的剪切闭锁等数值困难;②在较少自由度情况下,保证单元间应力的连续性以及精确满足力的边界条件;③保证一定精度的同时,加快大变形梁的计算效率;④采用绝对坐标以便于在柔性多体系统动力学各领域的应用.鉴于此,本文提出了一种可满足上述条件的空间几何非线性样条梁单元,该单元满足 Bernoulli-Euler 梁变形耦合关系,其广义应变与梁截面的刚体运动无关,可描述其几何非线性效应;样条单元的组装在满足内部节点应力连续的同时,缩减了系统自由度;边界节点参数包含应变参数,更加便于施加外力边界条件;降噪后的运动方程可采用通用的微分求解器快速求解;最后,通过数值算例验证了所提单元的有效性.
1 梁单元位移形函数
如图1所示,空间梁单元的两个节点分别为左右端面的形心,它们的矢径及其对弧长的一阶二阶导数选作为节点参数的一部分.
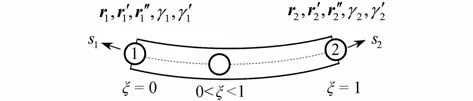
图1 空间梁单元Fig.1 A spatial beam element
形心线上的任意点矢径可以用五次多项式插值拟合得到
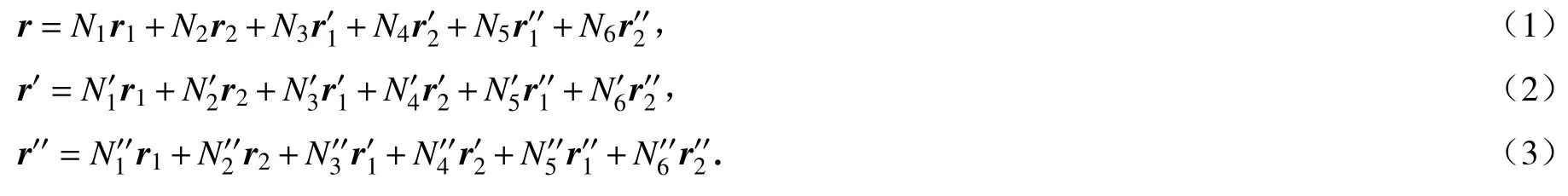
为简化符号,除非另有说明,本文中变量上标“′”表示变量对弧长坐标s的偏导数.式中的形函数
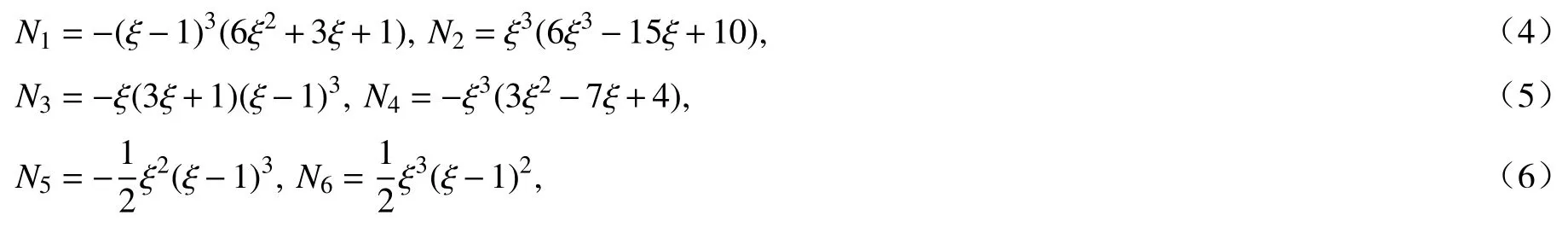
其中L为单元长度,归一化参数ξ 定义为

对式(1)求时间导数,可得

对式(2)求时间导数,可得

对式(3)求时间导数,可得
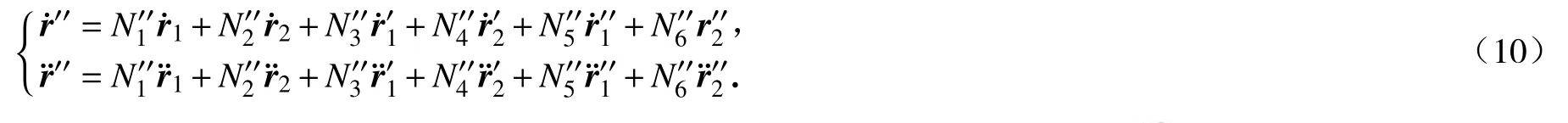
2 梁单元的转动描述
广泛采用的Euler 梁理论通过将截面视为刚性截面,将三维问题转化为一维问题.为了描述截面的运动,引入一个固结于截面形心的坐标系,第一根轴es沿截面的法线方向,其余两根轴et,eb分别指向截面的形心主轴方向,如图2所示.
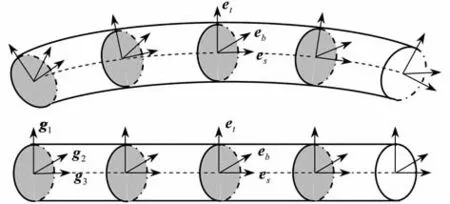
图2 梁单元截面坐标系Fig.2 The cross section coordinate system of the beam element
截面坐标系的位置和方位是时间t和形心线弧长坐标s的函数,它们的基矢量保持单位正交性,其对时间的导数可以用角速度表示:

类比角速度,引入曲率来描述截面基矢量对弧长坐标s的导数:

根据这样的定义,曲率和角速度在截面坐标系下分解为

式中,分解系数为

对式(14)求弧长导数和时间导数,可得

以及

将式(15)、(16)代入到式(13)知,角速度 ω的弧长导数可用曲率分量的时间导数表示:

曲率κ的时间导数可用角速度分量的弧长导数表示:

引入Euler-Bernoulli 梁假设:梁的截面法线方向始终与形心线的切线方向重合,即

其中,弧长伸缩率

对式(19)求时间的导数,可得

采用Cardan 角描述刚性截面的转动,将截面坐标系相对于总体坐标系 {g1,g2,g3}的转动分为三次相继定轴转动,转角依次为α,β,γ,则截面法向矢量可以表示为

因此,前两次转动的Cardan 角为

可以看出,Cardan 描述的转动对梁的截面运动有明确的物理意义,即前两次转动完全由梁的形心线的空间方位决定,第三次转动是绕着形心线的切线方向完成的,可将 α,β理解为绕截面的形心主轴方向的弯曲角度,将γ理解为扭转角度,避免了利用转动矢量进行插值来描述截面转动.
对式(22)求时间导数,可得

其中
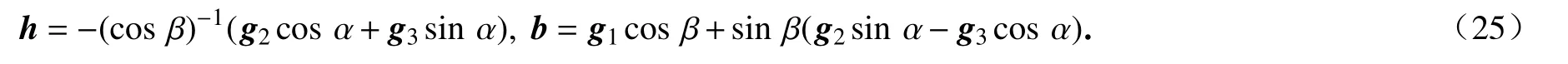
它们与es相互正交,基于此关系,容易得到Cardan 角对时间的导数为

对式(19)、(20)求时间导数,可得
由图5可知:改变条件后PID控制的超调更大且达到稳态所需的时间更长。对于ADRC控制,外加的干扰对其影响很小。
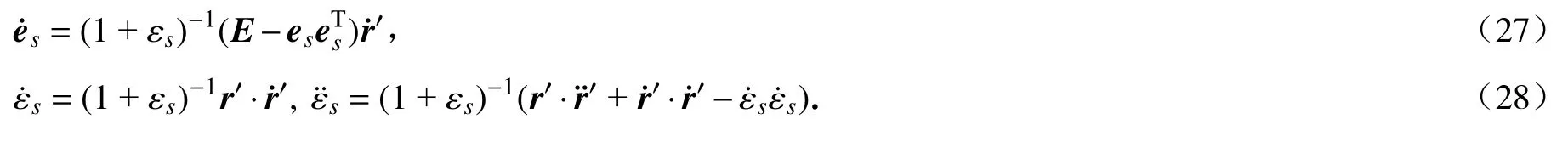
因此,式(26)可改写为

矢量h,b的时间导数可表示为

其中

同理,Cardan 角的弧长导数为
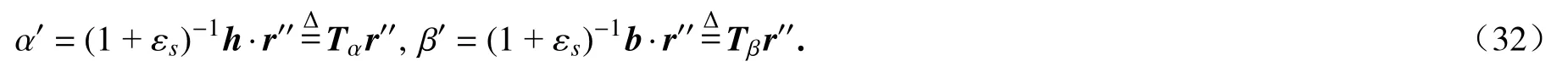
它们的时间导数为

其中

因此,式(33)可改写为

对式(29)求时间导数,可得

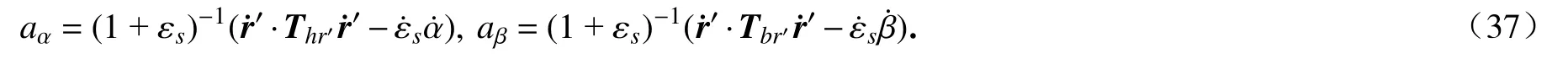
为了描述截面绕法线方向es的扭转,第三个角γ 被引入,采用三次多项式插值得到

它的形函数为

其中L为单元长度,归一化参数ξ 定义为

对式(38)、(39)求时间导数,可得
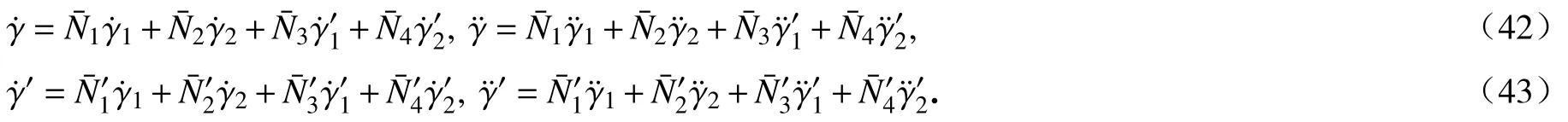
因此,截面坐标系形心主轴基矢量可用Cardan 角描述为
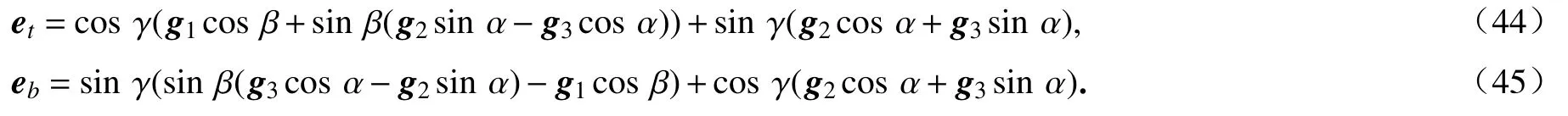
由上述可知,截面的转动可以采用Cardan 角描述,前两个Cardan 角可以表示为形心矢径的函数,第三个Cardan 角及其弧长导数可以在单元域内采用三次Hermite 插值得到.
3 梁单元的广义应变
如图3所示,从柔性梁中取出一小段原始弧长为ds的微元体,合力 -f和合力矩 -m作用在它的左截面.

图3 梁的微元体Fig.3 An infinitesimal beam unit
由刚体动力学方程可得微元体的运动方程为
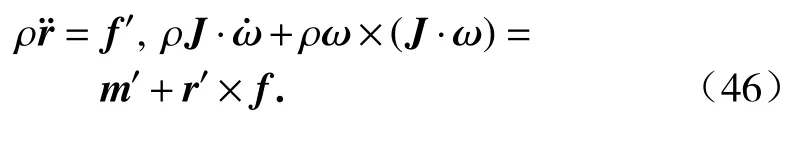
根据虚功率原理:外力虚功率为惯性力虚功率与变形虚功率之和,可得微元体的变形虚功率为
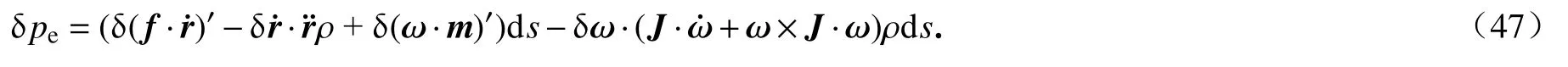
将式(46)代入到式(47),可改写为

将式(17)和(21)代入到式(48),可进一步简写为

其中力和力矩分量来源于

这表明,在截面刚性假设以及法向矢量与形心切矢共线的Bernoulli 假设情况下,梁的变形虚功率中的广义应变和应力应该表示为

相应的本构关系为

它的标准形式通常可改写为

式中,轴向应变 εs、曲率在截面坐标系中的分量 κs,κt,κb可认为是一组广义应变,它们都与梁的刚体运动无关,因而适用于几何非线性问题.
4 梁单元的角速度和曲率
定轴转动的角速度矢量的模等于转角的变化率,方向与转轴矢量方向相同.利用角速度叠加原理,采用Cardan 角描述转动的截面角速度矢量为

其中
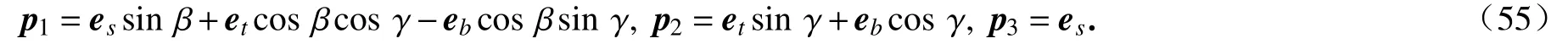
因此,它在截面坐标下的分量为
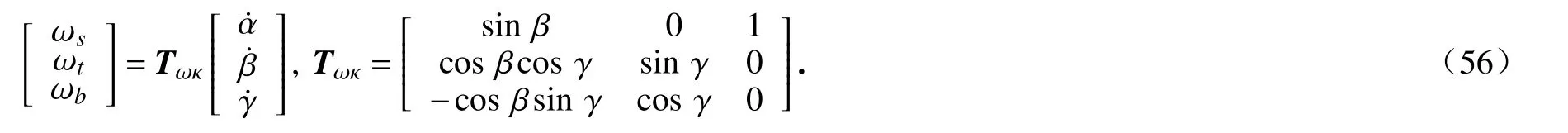
根据式(11)、(12)中角速度和曲率的定义,它们之间唯一的区别在于Cardan 角要么随时间变化要么随弧长变化,因此参考式(56),可得曲率分量为

对式(56)、(57)求时间导数,可得

其中,转换矩阵Tωκ的时间导数为

为了列式更加简洁,三个Cardan 角组成向量

据此,式(59)可改写为

其中
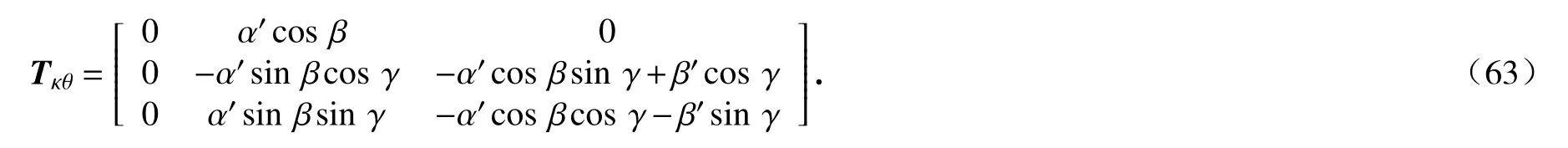
定义节点参数矢量组成的列向量:

从上述的分析可以看出,θ是节点参数q的函数,因此,它的时间导数可表示为
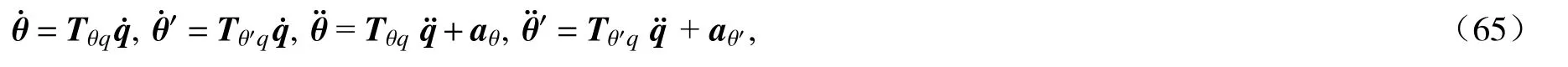
其中,转换矩阵Tθq,Tθ′q仅是q的函数,向量aθ,aθ′与加速度项无关.据此,角速度和曲率分量以及它们的时间导数可写为

其中
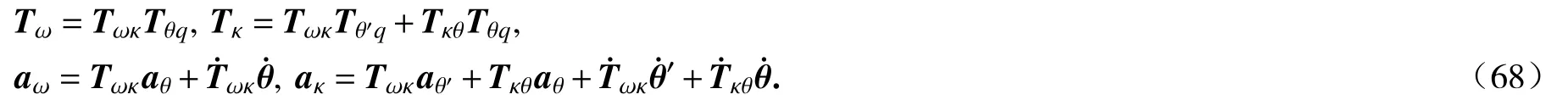
从式(58)、(59)和(36)可知,计算角速度和曲率的时间导数涉及矢径对弧长的二阶导数,为保证单元间应力连续,意味着在单元边界点处需要满足矢径对弧长导数的二阶连续性,这是选取五次多项式插值作为单元位移形函数的重要原因.
5 梁单元的质量阵和力阵
根据上述的讨论,单元内任意点矢径和应变的时间导数可以表示为以下的矩阵形式:

单元的惯性力虚功率为

其中,质量阵、力阵为
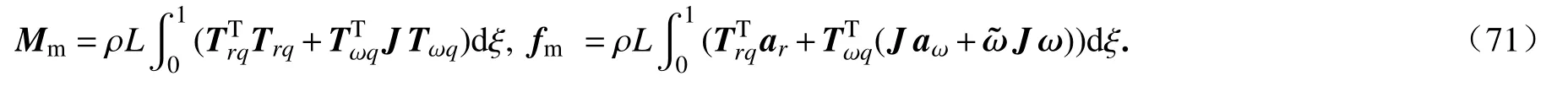
变形虚功率为

其中,弹性节点力为

经过单元组装,可得梁系统的虚功率方程为

其中,广义位移u是所有节点参数组成的列向量,fin,fa分别为广义内力和广义外力.为了进一步获得系统动力学方程,往往需要继续分析参数u的独立性.
6 梁单元间的连接光滑化
上述构造的梁单元每个节点上有11个节点参数,众多的自由度无疑会影响计算效率.如图4所示,为了缩减自由度,n-1个等长梁单元被组集为一个样条单元,内部节点矢径对弧长的导数r′k,r′k′(k≠1,k≠n)可以不作为单元的节点参数.它们是通过节点处矢径的三四阶弧长导数连续性要求确定(五次样条插值),即根据式(1)~(7),存在关系:

图4 缩减节点参数后的样条单元Fig.4 Parameter reduction of spline elements
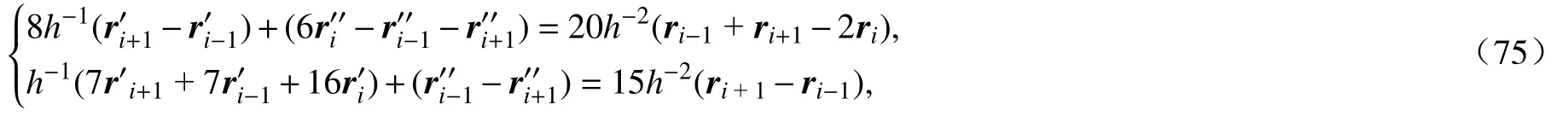
其中,单元长度

方程(75)写成矩阵形式:

式中,r′=[r′1r′2···r′n]为节点矢径对弧长坐标一阶导数的矩阵;r′′=[r′1′r′2′···r′n′]为节点矢径对弧长坐标二阶导数的矩阵;r=[r1r2···rn]为节点矢径的矩阵;系数矩阵都是(n+1)×(n+1)维三对角矩阵,可以表示为
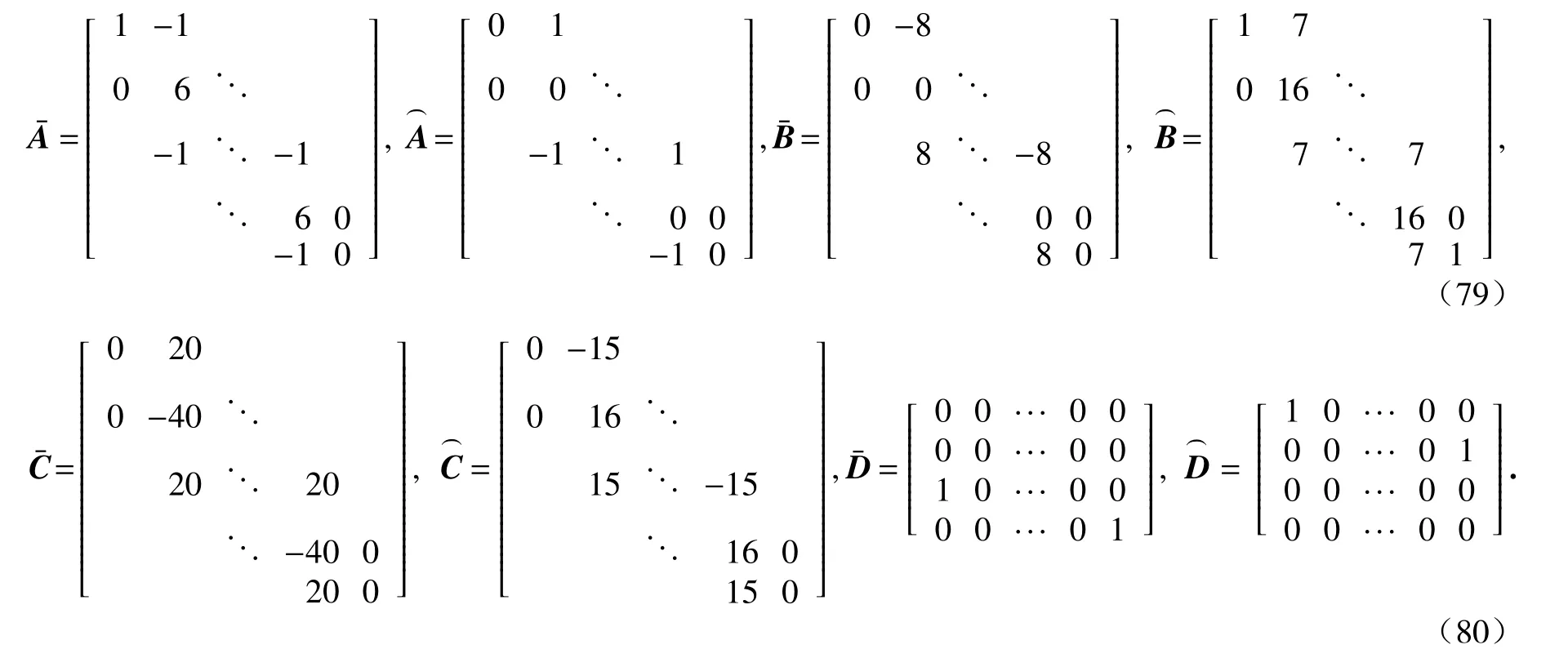

其中,矩阵

所有的系数矩阵均为常矩阵,对式(81)求导,可得
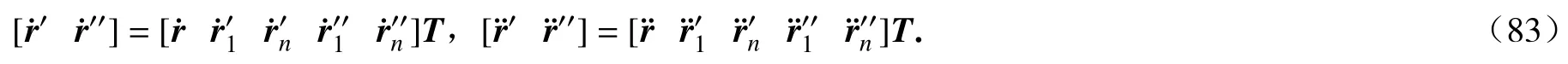
这样,可以采用样条单元直接建立梁结构的整体方程,内部节点处矢径对弧长的导数可以不作为节点参数,缩减系统的自由度,并且随着内部单元的增多,优势越明显.
7 样条梁单元边界节点参数转换
通过式(57),Cardan 角的弧长导数可以表示为
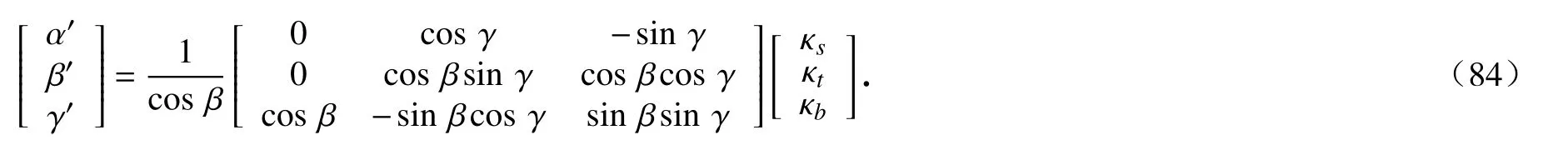
因此,边界节点处可以使用轴向应变的弧长导数 ε′s、Cardan 角α,β,γ 以及广义应变εs,κs,κt,κb代替矢径对弧长的导数作为节点参数,如图5所示.这样做的主要优势在于可以采用式(85)中简单的约束来精确满足力的边界条件,便于提高数值分析精度.
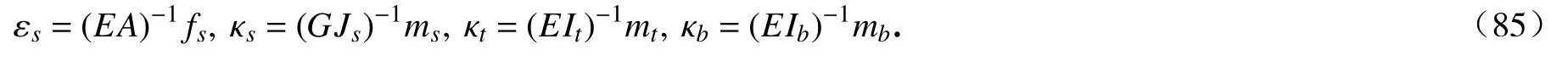
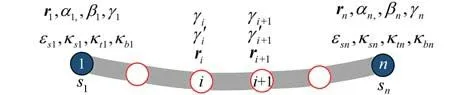
图5 样条单元的边界节点参数Fig.5 Boundary nodal parameters in spline elements
8 样条梁单元的降噪快速算法
梁结构在外力作用下,刚性截面发生大范围刚体运动的同时,还会有微幅高频的弹性运动,从常微分方程分类角度来看,由式(74)得到的梁结构动力学方程属于其解为慢变与快变分量混合的刚性微分方程.常用的刚性微分方程求解器ODE45 中为了准确求出高频振动,往往需要将步长调至很短,这极大地增加了计算代价;相关数值方法的主要思想是在积分格式中引入数值阻尼滤掉系统的高频分量,从而加快求解速度,其实这个过程可以在建模过程通过将应力替换为极短时间内的平均应力来完成[32].
在t+τ时刻,单元应力可以近似表示为

它在极短时间区间(t,t+Δt)内的平均值为


上述分析中梁单元的变形虚功率改写为

式中

其中,fe由式(73)定义,加速度无关项aε来源于

从式(89)可见,采用极短时间区间内平均应力代替瞬时应力后,系统方程中增加的阻尼项和内力项会保持低频分量不变,而快速衰减模型中的高频分量.光滑因子的选择应该综合计算效率和模型精度后进行合理确定,根据大量的计算经验,光滑因子的推荐值为0.000 1<Δt<0.01.
9 数值算例
为检验所提单元的合理性,分析了5个算例,其中算例1、2 检验了模型的滤除高频成分,加快计算效率的可行性,以及柔性部件变形大小对单元的有效性;算例3 验证了单元内部广义应变的连续性;算例4、5 证明了单元适用于任意空间大转动问题,且与解析解、相关文献进行了对比.
9.1 算例 1:单摆机构自由下落
L=5 mA=π ×10-2m2ρ=7 850 kg/m3
如图6所示,摆长为,截面积均为,材料密度为,弹性模量为E=2.1×1011Pa的机构在y轴方向g=-9.8 m/s2重力加速度下,从图示静止位置落下.
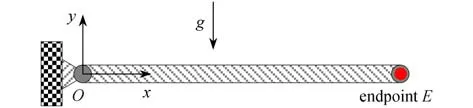
图6 自由下落的柔性单摆机构Fig.6 The free-falling flexible pendulum mechanism
应用本文所提单元将单摆作为一个样条梁单元,内部划分4个小单元,采用ODE45 求解器,其中光滑因子分别取 Δt=0,0.001,0.01,0.1进行数值积分,取精度控制参数相 对误差 εr=1×10-3和 绝对误差εa=1×10-6.得到单摆机构上末端点沿y和z方向的速度变化,如图7所示.
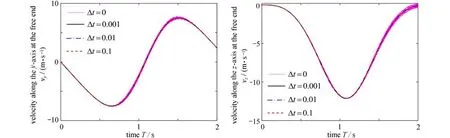
图7 末端点沿y 和z 方向的速度Fig.7 Velocities along y and z direction at the free end
由图7可以看出,当柔性单摆的材料刚度较大时(E=2.1×1011Pa),柔性梁的变形很小,当不使用快速降噪方法时(Δt=0),末端点的速度具有高频振荡分量,致使计算效率低下.采用本文所提降噪快速算法可使用非刚性微分方程求解器ODE45 求解该问题,且能够更好地滤除系统中的高频,得到更为平滑的变形曲线.
表1对比了上述不同方法的计算时间,结果显示本文所提快速算法可适用于普通ODE 求解器,且可大幅度提高计算效率.

表1 效率比较(柔性单摆机构)Table 1 Efficiency comparison (for the flexible pendulum mechanism)
9.2 算例 2:端部受剪力或力矩的悬臂梁
如图8所示,悬臂梁在端部受到集中剪力F或弯矩M作用,结构参数采用无量纲记法,梁的长度L=10,线密度 ρA=1,抗拉模量EA=104,抗弯抗扭模量GJ=EIy=EIz=103,截面初始构型惯性矩Jp=diag(20,10,10),梁的端部位移为ux,uy,来源于外力边界条件的受力端节点的应变约束为
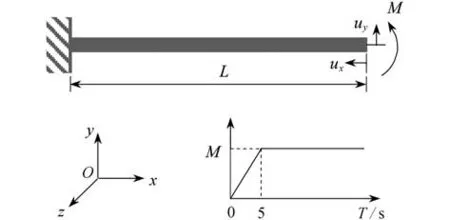
图8 悬臂梁自由端受力矩作用Fig.8 A cantilever beam subjected to an end moment
① 当端部受力矩M作用时,εs=0,κs=0,κt=M/(EIz),κb=0;
② 当端部受剪力F作用时,εs=0,κs=0,κt=0,κb=0.
这里将梁作为一个样条单元,内部取3个节点进行计算,ODE45 求解器参数设置为相对误差εr=1×10-3,绝对误差 εa=1×10-6.当端部受弯矩作用,悬臂梁发生纯弯曲,存在解析解 κ=M/(EIz),即发生纯弯曲时弯曲曲率κ 与外力矩M成正比,外力矩M=2πL-1EIz时,梁弯成一个圆.表2和图9、10 分别给出了悬臂梁受弯矩M=2πL-1EI作用时选取不同光滑因子 Δt仿真所用时间及得到的端部位移随时间变化的曲线.

表2 悬臂梁受集中力矩 M=2πL-1EI 时选取不同光滑因子仿真用时Table 2 The simulation time of different smoothing factors for the cantilever beam subjected to an end bending load M=2πL-1EI
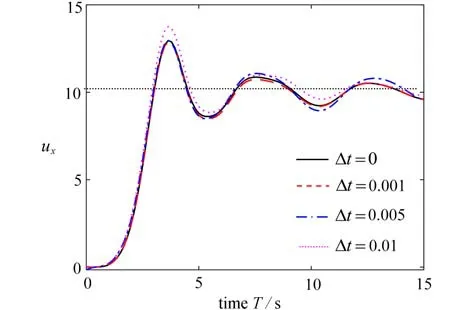
图9 悬臂梁受集中力矩作用的位移ux 曲线Fig.9 End displacement ux of the cantilever beam with an end bending moment
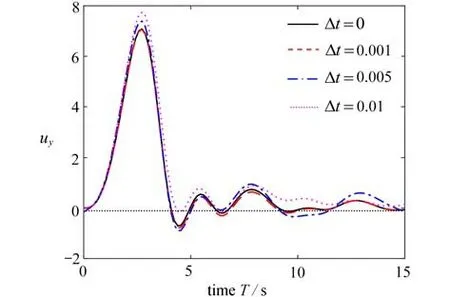
图10 悬臂梁受集中力矩作用的位移uy 曲线Fig.10 End displacement uy of the cantilever beam with an end bending moment
从图中可知,当光滑因子 Δt为0.001 时,梁的端部位移与不采用降噪方法(Δt=0)时计算的结果相吻合,最大绝对误差在0.1 以内,但耗时从3 653 s 缩短至982 s,若对精度要求不高,继续增大光滑因子,耗时将进一步缩短.图11、12 给出了在不同弯矩作用下梁最终平衡时的变形状态及其端部位移与解析解的对比,文献[33-34]已经指出形心位移和转角独立插值的传统梁,解决诸如此类发生大弯曲变形细长梁时,会出现剪切闭锁造成误差增大的现象,对比曲线显示本文单元计算结果与解析解吻合较好,无剪切闭锁的发生.
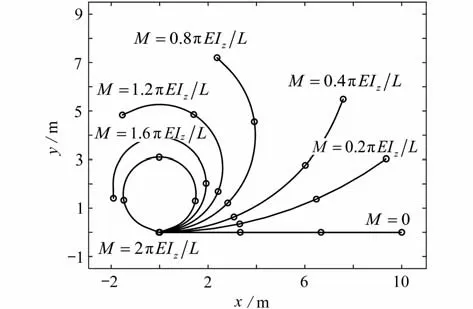
图11 悬臂梁在不同弯矩作用下的变形曲线Fig.11 Large deformation curves of the cantilever beam under different bending moments
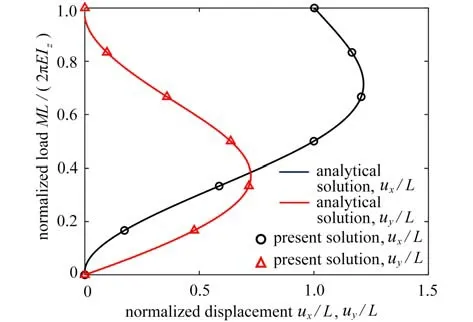
图12 悬臂梁受集中力矩的位移曲线Fig.12 The displacements of the cantilever beam with an end bending moment
当端部受剪力作用处于平衡状态时,小变形范围内端部位移存在解析解uy=FL3(3EIz)-1,大变形结果可采用ANSYS 软件打开“NLGEOM”命令给出合理的解.表3和图13给出了采用本文单元建模,不同剪力作用下梁最终平衡状态下端部竖向位移,以及和解析解、ANSYS 结果的对比.由表3和图13可知,剪力大小在1~3 N 范围内时,梁的变形属于小变形,与解析解的误差在1%以内;随着剪力的增大,梁的变形逐渐进入大变形状态,在36 N 时变形位移已经超出梁长的1/2,此阶段,解析解已无法满足要求,本文计算结果与ANSYS 大变形计算结果误差随着剪力增大略微增大,但均在0.13%以内.
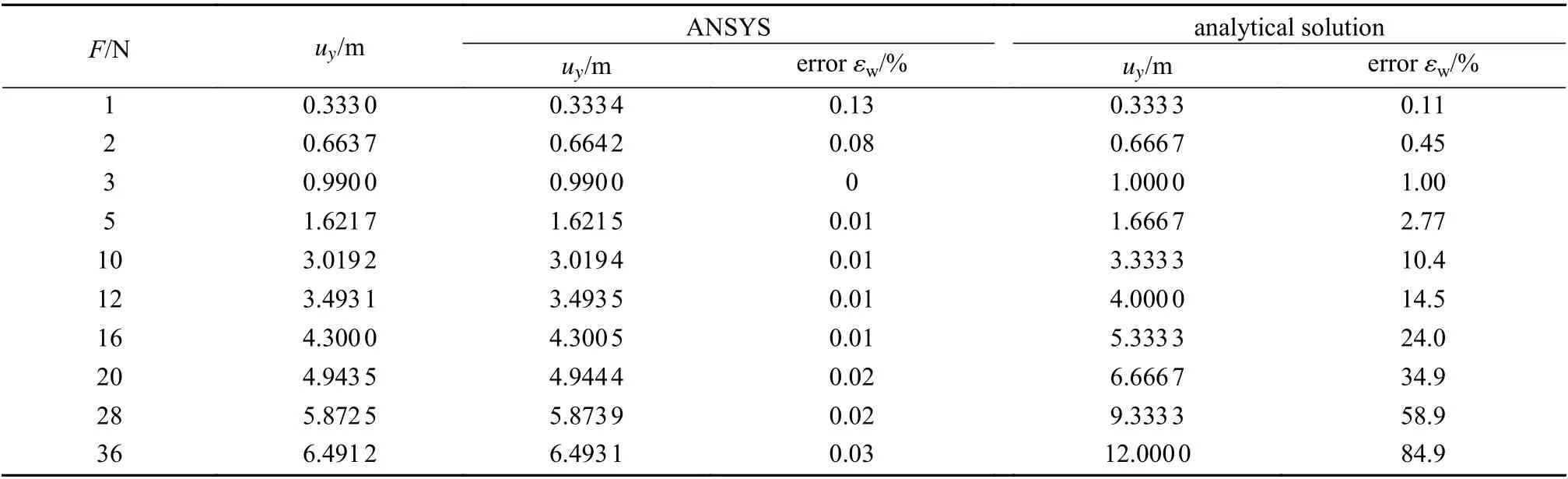
表3 悬臂梁不同剪力作用下平衡状态时竖向位移Table 3 Equilibrium deflections at the cantilever beam end under different shear forces
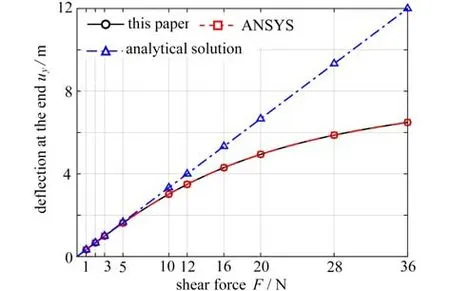
图13 悬臂梁平衡状态时竖向位移Fig.13 Deflections at the end in equilibrium
从上述分析结果可以看出,柔性梁无论处于小变形范围内还是发生大变形,乃至将梁弯成一个圆,本文所提单元计算的结果都可以得到准确的解,由此说明本文单元处理柔性梁部件变形的有效性.
9.3 算例 3:端部受剪力作用的旋转空间柔性梁
大范围运动的旋转柔性梁已被很多学者用来考察所提方法的有效性.如图14所示,梁的左端可以绕z轴自由旋转,右端施加y和z方向上两个随时间变化的动态载荷Fy(t)和Fz(t).梁的参数采用无量纲记法,长度L=10,线密度 ρA=1,抗拉模量EA=104,抗弯抗扭模量GJ=EIy=EIz=5×102,截面初始构型惯性矩Jp=diag(20,10,10).光滑因子取0.001,ODE45 求解器参数设置为相对误差 εr=1×10-3,绝对误差 εa=1×10-6,来源于外力边界条件的受力端节点应变约束为:εs=0,κs=0,κt=0,κb=0.
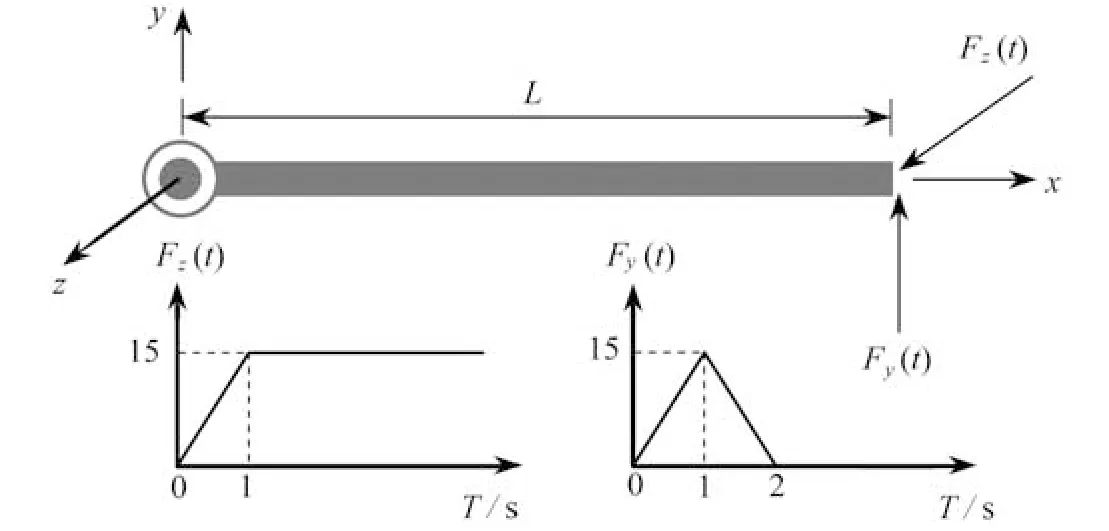
图14 旋转柔性梁初始状态及动态载荷Fig.14 The initial state and dynamic loads of the rotating flexible beam
图15给出了利用本文算法计算的结果与文献[35]对比的结果曲线.
从图15可以看出,旋转柔性梁端部的水平位移、竖直位移以及垂直纸面方向的位移呈周期性变化,且由于绕z轴转角没有限制的原因,水平位移幅值较大.本文内部含三个节点的一个样条单元(即内部有4个小单元)的仿真结果与文献[35]中20个单元仿真结果吻合得比较好.图16给出了15 s 和30 s 时梁截面的广义应变随弧长的变化曲线,数据显示梁的广义应变沿形心线是光滑连续的,依据本构关系可知广义应力同样沿形心线是连续的.
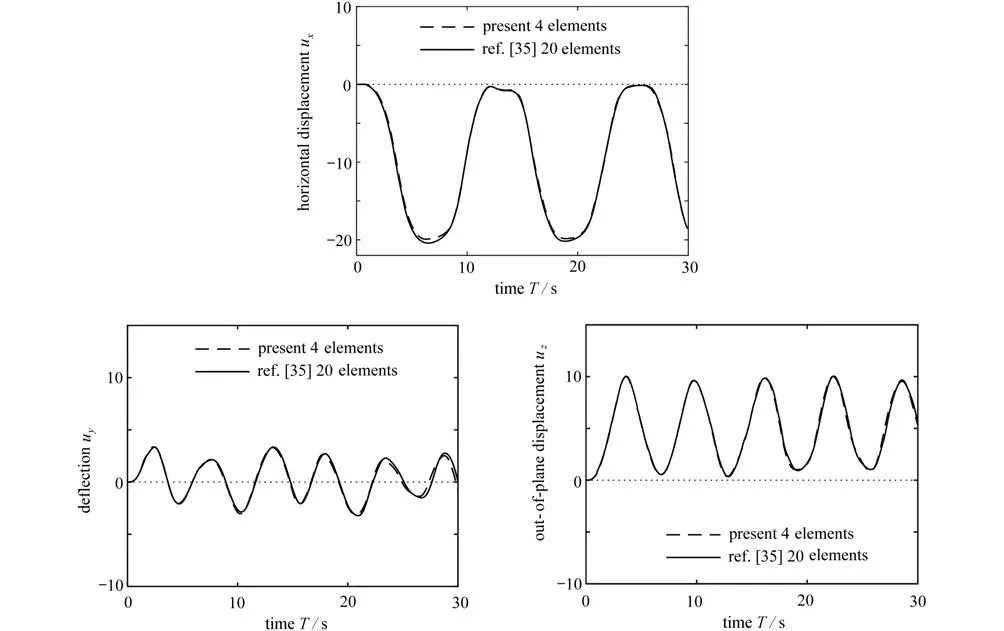
图15 旋转梁自由端的位移-时间曲线Fig.15 Displacement-time curves at the free end of the rotating beam
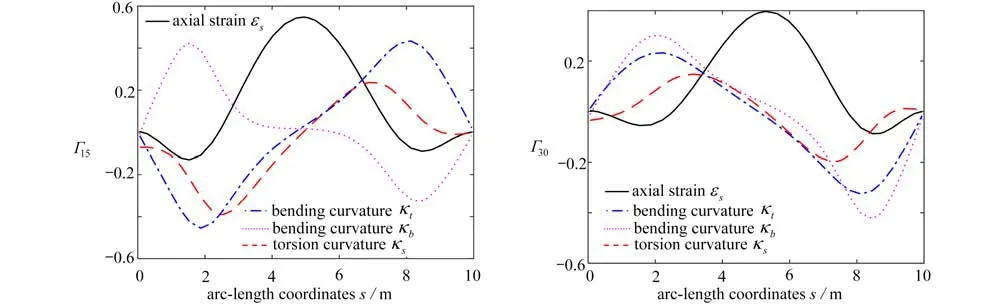
图16 时刻15 s 和30 s 时,旋转梁的广义应变Fig.16 Generalized strains of the rotating beam at 15 s and 30 s
9.4 算例4:弯头处受剪力作用的“L”形空间悬臂梁
如图17所示,“L”形悬臂梁的弯头处受指向面外的动态载荷Fz(t)的作用.载荷大小遵循图中所示的函数关系.结构参数采用无量纲记法,梁的长度L=10,线密度 ρA=1,抗拉模量EA=104,抗弯抗扭模量GJ=EIy=EIz=103,截面初始构型惯性矩Jp=diag(20,10,10).光滑因子取0.001,ODE45 求解器参数设置为相对误差εr=1×10-3,绝对误差εa=1×10-6.来源于外力边界条件的自由端节点应变约束为:εs=0,κs=0,κt=0,κb=0.
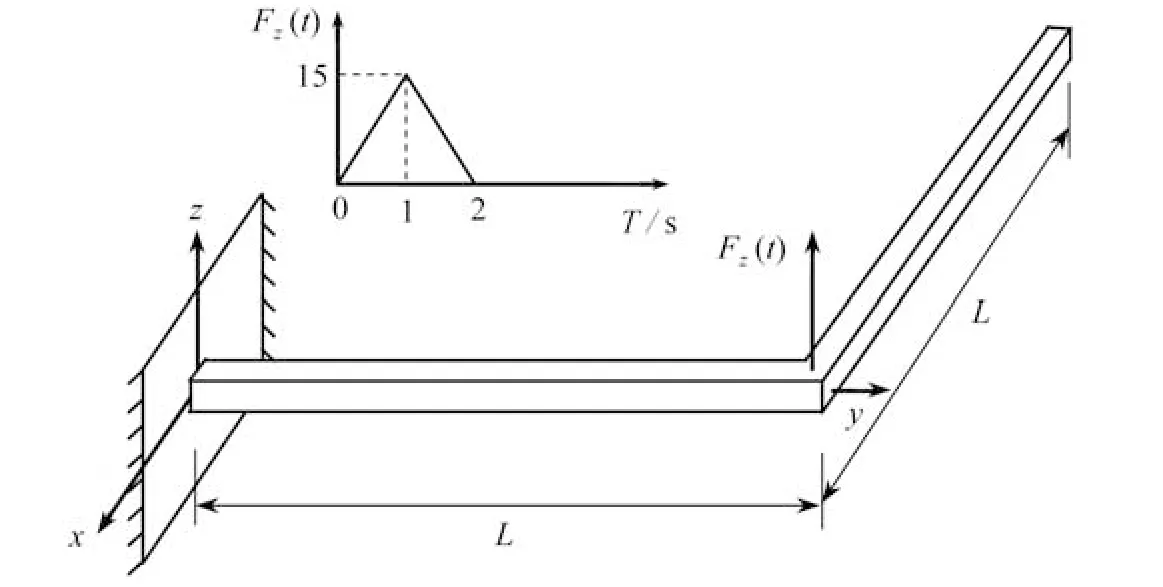
图17 “L”形悬臂梁初始状态及动态载荷Fig.17 The initial state and dynamic loads of the L-shaped cantilever beam
图18给出了利用本文算法计算的结果与文献[36]对比的结果曲线.
算例4 来源于文献[36],本文将“L”形悬臂梁的每个分支都用相同的样条梁单元表示,样条内部为一个节点(即内部含2个小单元,“L”形结构共4个单元)进行仿真.从图18可以看出,仿真结果中自由端与弯头处的z向位移与文献中采用20个单元的仿真结果相符合.“L”形悬臂梁自由端不受任何载荷作用,理论上此处广义应力均为零,图19中给出了自由端节点处轴线应变和截面曲率随时间的变化曲线,数据显示自由端节点处的轴向应变和截面曲率很小,在计算误差范围内,说明外力边界条件约束的准确性.
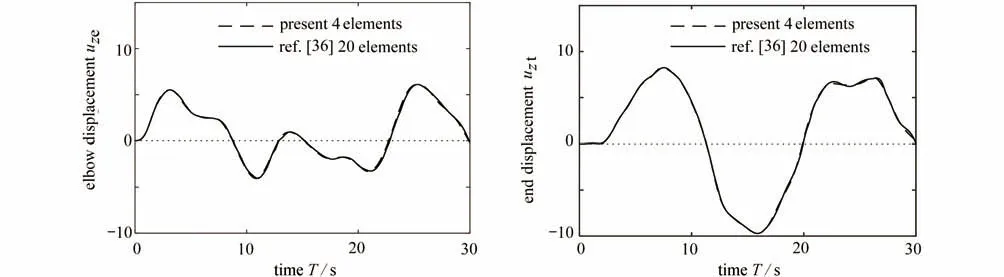
图18 “L”形悬臂梁自由端与弯头处的位移曲线Fig.18 The displacement curves at the free end and the elbow of the L-shaped cantilever beam
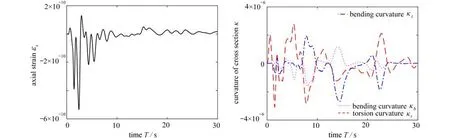
图19 “L”形悬臂梁自由端节点的广义应变Fig.19 Generalized strains at the free end of the L-shaped cantilever beam
9.5 算例5:端部处受组合力作用空间梁结构
如图20所示,三根单位长度梁垂直连接组成的空间结构的自由端受动态载荷F的作用.载荷大小遵循图中所示的函数关系,结构参数采用无量纲记法,梁的长度均为L=2,截面形式为0.1 × 0.1的正方形,弹性模量E=1×109Pa,Poisson 比 ν=0.3,密度 ρ=1 000 kg·m-3,光滑因子取0.001,ODE45 求解器参数设置为相对误差εr=1×10-3,绝对误差εa=1×10-6.来源于外力边界条件的自由端节点应变约束为:κs=0,κt=0,κb=0.
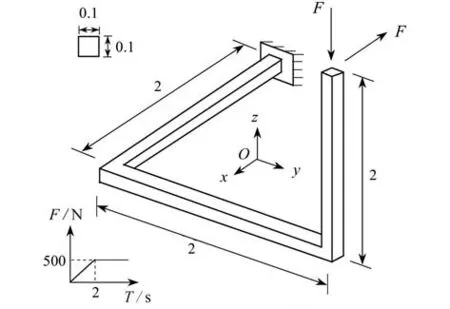
图20 空间组合梁结构Fig.20 A spatial structure composed of 3 beams
本文将空间组合梁结构的每个分支都用相同的样条梁单元表示,样条内部为3个节点(即内部含4个小单元,结构共12个单元)进行仿真.方便对比,采用ANSYS Workbench 对同样的结构进行动力学分析,提取受力端节点位移;得到本文计算结果与ANSYS 结果的对比曲线,如图21所示.
由图21可知,梁结构端部位移已经超过单个梁的长度尺寸大小,整个结构发生梁截面大位移大转动的变形,对比结果显示本文单元针对复杂空间梁结构计算的有效性.
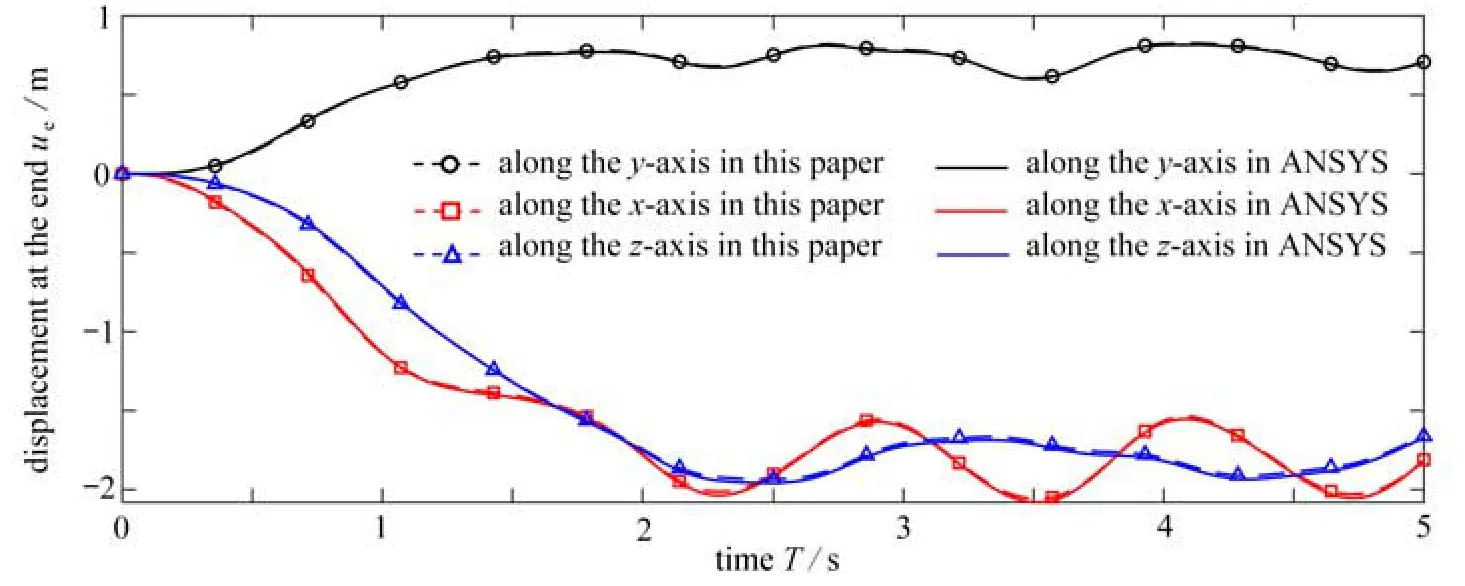
图21 空间组合梁结构受力端位移Fig.21 Displacements at the end of the spatial structure composed of beams
上述几个算例表明,在较大的载荷变化范围内,本文所得的结果与解析解、商业软件结果吻合得很好;相较传统梁单元离散方式,本文所提单元避免了位移和转角独立插值带来的剪切闭锁问题,采用样条插值,节点处导数连续性高、光滑性好,可以有效地求解大变形梁结构,保证了各分支梁内部节点处广义应力连续,滤掉刚性较强的梁结构中高频成分以在满足精度的要求下提高计算效率.此外,样条单元内部每一个节点参数为5个,要比传统的节点参数数量少,节点参数数目的优势会随着单元的增多而愈发明显.
10 结 论
实际工程梁结构中,诸如大型起重机伸缩臂结构、桁架式臂架结构等,它们的梁分支较多,大部分属于细长梁,往往伴随着大变形现象的发生,单元节点数可能成百上千.本文在大变形梁虚功率原理的基础上提出了一种节点参数含应变的几何非线性空间样条梁单元,它可以满足工程要求精度的同时,降低计算成本,具有以下几个特点:
1)传统几何非线性单元分析细长梁时,剪切闭锁造成的误差无法满足工程要求,本文考虑Euler-Bernoulli 梁变形耦合关系,建立梁单元转动参数和位移参数间的函数方程,可准确地仿真细长梁.
2)具有与截面刚体运动无关的广义应变(弧长伸缩率、截面曲率),可用于描述单元水平上的几何非线性问题;保证单元间应力连续情况下,采用样条插值进行自由度缩减式组装单元,将广义应变纳入到边界节点参数当中,便于精确地施加力的边界条件.
3)大变形梁的几何非线性效应以及刚性成分会使得计算效率十分低下,特别是在机械领域,往往关注的焦点是系统的宏观动力学行为,鉴于此,本文将梁结构系统方程进行降噪处理,滤掉其解中的高频成分,工程设计人员可根据精度要求的需要,适当调整光滑因子,保证要求精度的情况下,实现柔性梁的快速求解,降低求解空间几何非线性梁单元系统的计算成本.
本文的方法与经典算例的结果吻合度较高.在单元数目上少于文献中采用的单元数,而且中间节点参数数量较少,有利于缩减较多节点数目的工程梁结构的自由度规模.
