一类带扰动的随机脉冲泛函微分方程解的渐近性*

梁 青

（海南师范大学 数学与统计学院，海口 571158）

引 言

由于在机械工业、生物学、生态学、人口学和工程等方面的重要运用，随机微分方程(SDE)特别是随机泛函微分方程(SFDE)，越来越多地受到研究者们的关注[1-12].SFDE的许多性质都是研究的热点，比如方程解的存在唯一性、有界性、持久性和各种类型的稳定性等.而在SDE的诸多性质中，有一种性质不论是从理论还是从应用的角度看都很有价值，那就是受扰动SDE的性质，文献[13-15]对不同类型的带扰动SDE的性质做了详细的讨论.另一方面，脉冲效应是自然界中普遍存在的现象，它的影响不容忽视，例如，它可以使一个非稳定系统稳定化.脉冲在物理、化学、生物、人口动力学和工业自动化领域被广泛应用[16-19].基于脉冲效应对SFDE的重要意义，我们很自然地要研究带有脉冲SFDE的解和不带脉冲SFDE的解具有哪些不同的性质.文献[15]研究了在系数满足Lipschitz 条件和线性增长条件的前提下，受扰动SFDE的解和未受扰动SFDE的解在有限区间上是相互逼近的，而且，当扰动项趋于零时，区间长度趋于无穷大，这两个解在该无限区间上也是相互逼近的.如果文献[15]中的SFDE 含有脉冲干扰，方程的解不是连续，而是分段连续的，那么，文献[15]中的结论是否成立?为了研究这个问题，本文从一类带有脉冲时刻的SFDE 出发，利用Itô公式、基本不等式和随机分析技巧，在较弱的的条件下证明了受扰动方程的解和相应的未受扰动方程的解在有限区间上是相互逼近的.而且，当扰动项趋于零时，这两个解在长度趋于无穷大的时间区间上也是相互逼近的.本文不同于文献[15]之处在于：① 把脉冲的干扰引入方程，使系统变得更加复杂和完备，证明了带脉冲的方程的解也有类似的结果；② 把文献[15]中加在方程系数上的Lipschitz 条件和线性增长条件弱化，在较弱的条件下证明了类似的结论.所以本文涵盖了文献[15]中的相关结果，是对文献[15]的推广.

1 准备工作

设(Ω,F,{Ft}t≥0,P)是一个带流的完备概率空间，流 {Ft}t≥0满足通常条件，E是关于概率测度P的数学期望，本文中所有的随机变量和随机过程都定义在该概率空间上.向量或矩阵A的转置记为AT.设 Z+和 R+分别表示非负整数和非负实数，Rn表示n维欧氏空间，|·|表示 Rn中的欧氏范数.如果A是一个矩阵，用记为它的Frobenius 范数.令 {B(t)=(B1(t),B2(t),···,Bn(t))T:t≥0}是关于 {Ft}t≥0适应的n维Brown 运动.设τ＞0,p≥2是常数，L2([-τ,0];Rd)表示取值于 Rd的Borel 可测函数 ψ1(s):-τ≤s≤0构成的族，L2([-τ,0];Rd)中的范数定义为

设CF0([-τ,0];Rd)表示从[-τ,0]到 Rd的关于 F0可 测的分段连续的随机过程ψ2(s)的全体，且ψ2(s) 在[-τ,0]的间断点处右连续有左极限，这里Fs:=F0,s∈[-τ,0].该空间的范数定义为

L2([-τ,0]×Ω;Rd)表示取值于 Rd空间中的Borel 可测的随机函数ψ3(s):-τ≤s≤0 构成的族，其中的范数定义为

这里，µ是([-τ,0],B([-τ,0]))上的概率测度.

考虑下列带有脉冲的SFDE：

其中，ξ ∈CF0([-τ,0];Rd)，且E‖ξ‖2p＜+∞；x(t)=(x1(t),x2(t),···,xd(t))T，xt={x(t+θ):-τ≤θ≤0}是取值于L2([-τ,0];Rd)的随机过程；tk表示脉冲时刻，k=1,2,3,···，tk＜tk+1，且 limk→+∞tk=+∞，Ik(tk,x(tk))表示x在tk时刻的跳的幅度；f:R+×L2([-τ,0];Rd)×R+→Rd，g:R+×L2([-τ,0];Rd)×R+→Rd×n是两个Borel 可测函数.

为了得到本文的结果，先给出以下假设：

p1≥1t≥0,y＞0,y′≥0,φ ∈L2[-τ,0;Rd],φ′∈L2([-τ,0];Rd)

(A1) 设，对任意的，有

其中，ρ1(·):R+→R+是单调递增的连续的凹函数，ρ1(0)=0，且

(A2) 存在常数K1＞0，对任意的t≥0，

|f(t,0,0)|∨|g(t,0,0)|≤K1.

(A3) 存在常数K2，K3＞0，使得对任意的t≥0和 自然数k，以及x,y∈Rd，有

|Ik(t,x)-Ik(t,y)|≤K2|x-y|,|Ik(t,x)|≤K3.

若假设(A1) 对p1=1成立，则假设(A2)、(A3) 也成立，则由文献[19] 可知方程(1) 存在唯一解，记为x(t).而且，由文献[18]可知x(t)几 乎必然在t≥0时 右连续有左极限，不连续点只可能在脉冲时刻tk处取得，k=1,2,3,···.

现在，再来考虑受扰动的SFDE：

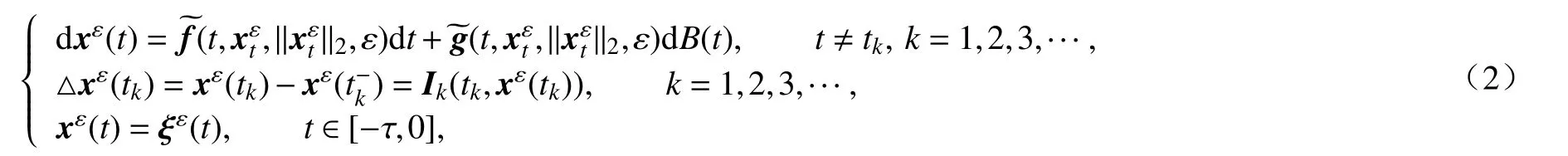
其中，ε是常数，0＜ε＜1，ξε∈CF0([-τ,0];Rd)，且E‖ξε‖2p＜+∞；xε(t)=(xε1(t),xε2(t),···,xεd(t))T，xεt={xε(t+θ):-τ≤θ≤0}是取值于L2([-τ,0];Rd)的随机过程；R+→Rd×n是两个Borel 可测函数.而且，对任意t＞0,φ ∈L2([-τ,0];Rd),y≥0，有

其中，α,β称为扰动参数，方程(2)称为扰动方程.

(A1′) 对任意的t≥0,y＞0,y′≥0,φ ∈L2[-τ,0;Rd],φ′∈L2([-τ,0];Rd)，有

其中，ρ2(·):R+→R+是单调递增的连续的凹函数，ρ2(0)=0，且

(A2′) 存在常数K4＞0，对任意的t≥0,ε＞0，

假设(A1′)、(A2′)和(A3)成立，则由文献[19]可知方程(2)存在唯一解，记为xε(t).而且，由文献[18]可知xε(t)几 乎必然在t≥0时 右连续有左极限，不连续点只可能在脉冲时刻tk处取得，k=1,2,3,···.

再给出一个有用的引理.

引理1(Bihari 不等式)[20]设T1＞0,ω0≥0，ω (t),v(t)是区间[0,T1]上的连续函数，u(·):R+→R+是单调递增的连续的凹函数，对任意的r＞0，有u(r)＞0.若则的逆函数.特别地，如果则ω (t)=0,t∈[0,T1].

2 主要结果及证明

在这一节中，我们将利用Itô公式、基本不等式和随机分析技巧，证明以下的引理2，进而得到了本文的主要结果定理1 和定理2.

t0:=0 △x(0)=0,△xε(0)=0t≥0

首先，补充定义.假设.对任意的，定义

引理2假设(A1)对p1=1,2和p都 成立，则假设(A2)、(A3)、(A1′)、(A2′)也成立，且存在δi(ε)≥0,limε→0+δi(ε)=0(i=1,2,3,4)满足以下条件：

则对任意t≥0，有

其中，Mi(ε)是依赖于p,ε的正数，且l imε→0+Mi(ε)=0(i=1,2,3)；M4,M5是依赖于p的正数.

证明由方程(1)可得对任意正整数k，有

所以，当s∈[0,t]时，存在ns∈Z+，使得tns≤s＜tns+1，且

同理

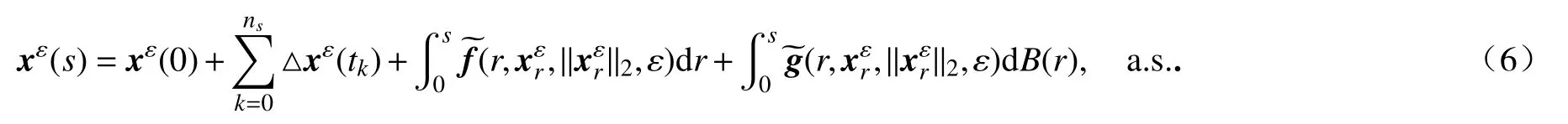
由式(5)和(6)得

对|zε,1(s)|p用Itô公式，得

当r＞0时，

由于p≥2，利用Jensen 不等式，得

由式(9)得

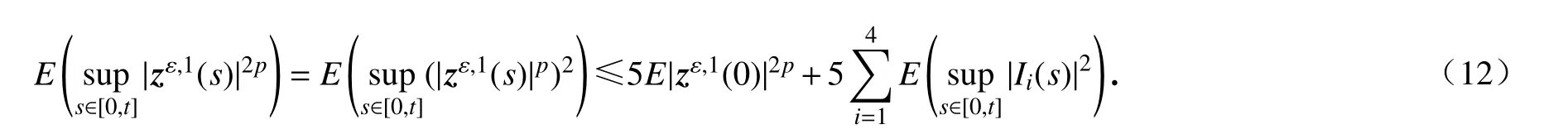
下面分别估计E(sups∈[0,t]|Ii(s)|2),i=1,2,3,4.

利用BDG 不等式、Young 不等式[20]、Jensen 不等式、假设(A1)、式(10)和式(11)，得

利用Hölder 不等式得

与式(13)类似，有

利用Hölder 不等式和Young 不等式[20]，可得

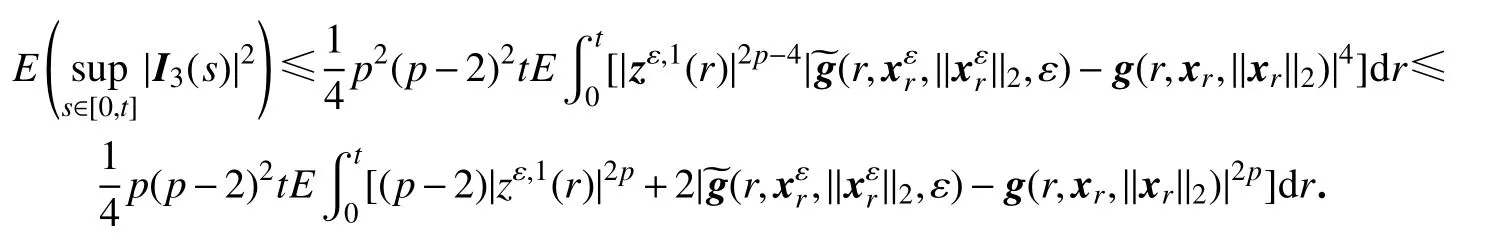
接下来估计E(sups∈[0,t]|I1(s)|2).同理可得

同理可得

注意到

E|zε,1(0)|2p=E|zε(0)|2p≤δ1(ε),

所以

由式(12)～(17)可知式(3)成立，其中M1(ε),M2(ε),M3(ε),M4,M5取值如下：

下面给出本文的主要结果.

定理1设0＜ε＜1,T＞0是常数，引理2的条件全部满足，则

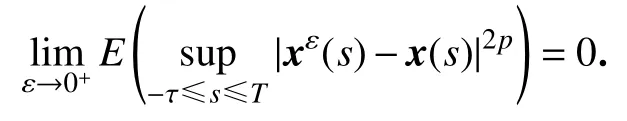
此外，设q1是常数，且0＜q1＜2，则

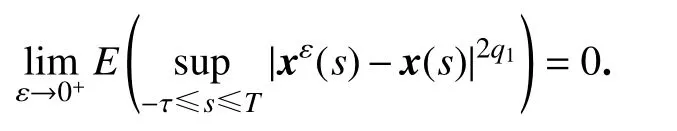
证明易知存在唯一的n0∈Z+，使得tn0≤T＜tn0+1.由引理2，对任意的t∈[0,tn0+1]有

这里 ρ*(s):=s+ρ1((τp+1)s),s≥0.

由于xε(t)和x(t)在 (tk,tk+1)内 连续，在tk处右连续有左极限，a.s.，k=0,1,2,···.因而zε(t)在 (tk,tk+1)内连续，在tk处右连续有左极限，a.s.，k=0,1,2,···.从而 |zε(t)|2p在(tk,tk+1)内 连续，在tk处右连续有左极限，a.s.，k=0,1,2,···.所以 s up-τ≤s≤t|zε(s)|2p在 (tk,tk+1)内 连续，在tk处右连续有左极限，a.s.，k=0,1,2,···.所以 Δε(t)在 (tk,tk+1)内连续，在tk处右连续有左极限，k=0,1,2,···.

任取t*∈(tk,tk+1)，则对任意的ε1＞0，存在δ1＞0，当tk＜t*-δ1＜t＜t*+δ1＜tk+1时，

|Δε(t)-Δε(t*)|＜ε1.

所以

同理，l imsupε→0+Δε(t*)-limsupε→0+Δε(t)≤ε1.所以l imsupε→0+Δε(t)在t*处连续.

类似可证l imsupε→0+Δε(t)在tk处右连续有左极限，k=1,2,3,···.

由式(18)可得，当t∈[0,tn0+1]时，

注意到

且

所以

显然，ρ*(·)是[0,+∞)上单调递增的连续的凹函数，且ρ*(0)=0.

由于l imsupε→0+Δε(t)在 [0,t1)上连续，在t1处有左极限，由式(19)和引理1 可得

设δ ∈[0,t2-t1)，则t1+δ ∈[t1,t2).

由于l imsupε→0+Δε(·)在 [t1,t2)上连续，在t2处有左极限，由式(19)可得

再由引理1 可得

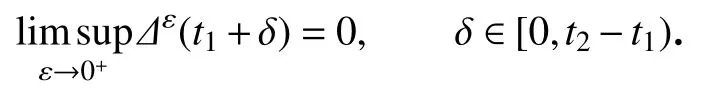
重复以上过程有限次，可得

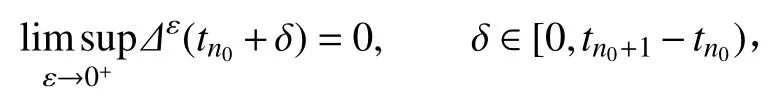
所以

由于0＜q1＜2，用Lyapunov 不等式，当时，

定理2假设引理2的条件都满足，则对于任意的ε ∈(0,1)，存在T(ε)＞0，l imε→0+T(ε)=+∞，使得

此外，设q2是常数，且0＜q2＜2，则

证明任取η＞0.分两种情况讨论：

t∈(0,+∞) Δε(t)＜η

(Ⅰ) 对任意的，都有.此时

所以

所以，对任意的T(ε)＞0,limε→0+T(ε)=+∞，都有

η的任意性证明了

rε∈(0,+∞) Δε(rε)=ηt＞0

(Ⅱ) 存在，使得.此时，利用引理2,对任意的，有

假设rε有界，即存在＞0，使得0＜rε＜.所以

而由定理1 可得

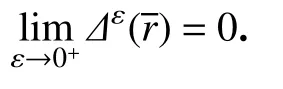
这是一个矛盾.所以

设0＜ε′＜ε′′＜1，以及rε′＜rε′′,则

η2=Δε′(rε′)≤Δε′(rε′′).

而由定理1 可得

这又是一个矛盾.所以

rε′≥rε′′.

即rε关于ε 在 (0,1)内单调递减，所以

记

则有

在式(20)中，令η→0+，得

再令t=T(ε)，得

所以

由于0＜q2＜2，用Lyapunov 不等式，当ε→0+时，

注1文献[15]研究了不受脉冲影响的SFDE，在一定条件下证明了扰动方程的解和未受扰动的方程的解是相互逼近的.在本文中，如果不考虑脉冲的影响，则本文的式(1)和(2)就变成文献[15]中的式(2)和(4).本文把脉冲影响引入到系统中，此时SFDE的解在脉冲点处是右连续有左极限的，在适当的条件下，本文证明了扰动方程的解和未受扰动的方程的解也是相互逼近的.因此，本文涵盖了文献[15]中的相关结果.

注2为了证明扰动方程的解和原方程的解相互逼近，文献[15]中对方程的系数做了两点假设，即Lipschitz 条件和线性增长条件.本文对这两个条件进行了适当的弱化，得到了假设(A1)、(A2)、(A1′)、(A2′).事实上，如果令本文的ρi(s)=Ks,i=1,2.本文的假设(A1)、(A1′)就变成了文献[15]中的条件，因而本文是文献[15]中结论的推广.

3 算例验证

在这一节中，设ξε=ξ，前两节中的n,d,τ,tk取值分别为

n=1,d=1,τ=0.1,tk=k,k=0,1,2,···.

对t≥0,φ ∈L2([-0.1,0];R),y≥0,定义

f(t,φ,y):=‖φ‖L2+2y,g(t,φ,y):=‖φ‖L2+y.

可以验证，对p1=1,2和p，以上定义的f和g满足假设(A1) 和(A2).对t≥0,φ ∈L2([-0.1,0];R)，y≥0,0＜ε＜1,定义

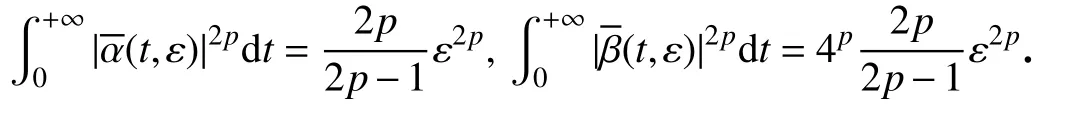
对t≥0,x∈R和 自然数k，定义Ik(t,x):=arctanx，则假设(A3)成立.

考虑下列带有脉冲的SFDE：

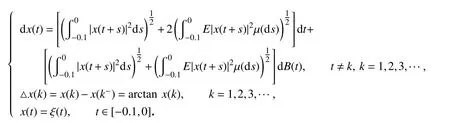
它的扰动方程是

假设

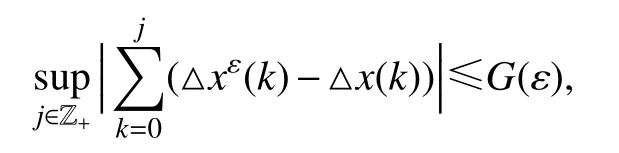
其中，l imε→0+G(ε)=0.则引理2的条件全部满足，所以本文的结果定理1 和定理2 成立.

4 结 论

基于脉冲现象的普遍性，本文探讨了一类带脉冲影响SFDE的解的渐近性.在较弱的条件下证明了受扰动的方程的解和原方程的解在有限的时间区间上是相互逼近的，而且，当扰动趋于零时，时间区间变为无穷区间，两个解在这个无穷区间上也是相互逼近的.本文推广了SFDE的解的渐近性的相关结果.