时空多项式配点法求解三维Burgers方程*

曹艳华，张姊同，李 楠

（华东交通大学 理学院，南昌 330013）

引 言

Burgers 方程可以用来模拟冲击波的传播和反射，是一个被广泛应用于流体力学、非线性声学、气体动力学等领域的非线性偏微分方程[1-3].由于Burgers 方程是从Navier-Stokes 方程简化而来，因此对于该方程的研究众多，其中不乏非常有意义的研究成果.Hopf[2]和Cole[4]提出了著名的Hopf-Cole 变换来研究Burgers 方程的基本性质.他们发现Reynolds 数对于平衡方程中的非线性对流项和黏性扩散项起着举足轻重的地位.当Reynolds 数变大的时候非线性对流项占主导地位，由此导致了Burgers 方程的强非线性性，使得其求解异常困难.尽管通过Hopf-Cole 变换可以求得一些特殊类型Burgers 方程的精确解，但对于绝大多数Burgers 方程而言，其精确解是难以得到的.学生在学习Burgers 方程的强非线性理论时，不易理解其含义[5-7].

Gulsu 使用有限差分法求解具有小Reynolds 数的Burgers 方程[8]，对于具有大Reynolds 数的Burgers 方程，有限差分法的求解精度很差[9].Turgut 等采用半步长方法[10]，即时间方向采用半隐式有限差分格式、空间方向采用渐进展开格式求解具有大Reynolds 数的Burgers 方程.除了采用传统的网格类方法，近些年来，无网格类方法也被广泛用来求解Burgers 方程[11-17].

所谓时空类方法，即在求解发展方程时将时间变量t视为普通的空间变量x，其中著名的时空类方法有时空有限元法[18]、间断Galerkin 有限元法[19]以及Mohammed 等提出的局部时空径向基函数等方法[20].

2017年，Dangal 等提出了一种新的多项式特解法用于求解偏微分方程[21].2020年，Cao 等在多项式特解方法的基础上，提出了一种时空多项式特解法求解一维和二维的发展方程[22-23].受其启发，本文采用时空多项式特解法求解三维具有大Reynolds 数的Burgers 方程.相比于其他的无网格类方法，多项式特解配点法只需知道配点的位置信息，别的任何未知参数都不需要确定，其简便性远远超过现有的其他时空类无网格方法，例如，使用时空径向基函数方法时，不仅需要确定径向基函数的形状参数，还需要确定配点的中心位置、个数以及插值半径，这些参数的确定没有一般规律可循.数值例子表明，随着Reynolds 数的增加，时空多项式特解法不仅可以保持数值解的高精确性，其稳定性也没有受到任何影响.

注1所有以多项式作为基函数的方法中，由于系数矩阵随着多项式阶的增加，其条件数迅速增大，很快数值溢出，因此本文的所有算例均采用了多尺度技巧以降低系数矩阵的条件数，得到稳定的数值解[22].

注2多尺度技巧可以有效降低多项式特解中系数矩阵的条件数，但对于多项式直接作为基函数得到的系数矩阵，多尺度技巧不能有效降低系数矩阵的条件数，这也是多项式函数直接作为基函数求解三维Burgers 方程得到的近似解精度不高的原因之一.

1 时空多项式特解法

考虑如下的三维偏微分方程初边值问题：

其中，Ω为三维空间中一有界连通的规则或不规则区域，f(x,t),g(x,t)和h0(x)为给定函数，∂t=∂/∂t，L为线性或非线性偏微分算子，B为边界算子，(0,τ]为待求时间区间.

在时空类方法中，需要将三维待求解问题转化为相应的四维问题，新的“空间变量”为“t+(x,y,z)”，将Ω×{t=0} 和 ∂Ω×(0,τ)作为新四维问题的边界.在时空类方法中，不再区分时间变量t和 空间变量x=(x,y,z)，因此，相应于方程(1)的新四维问题为

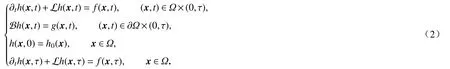
在新四维空间中，d阶完全多项式基函数为

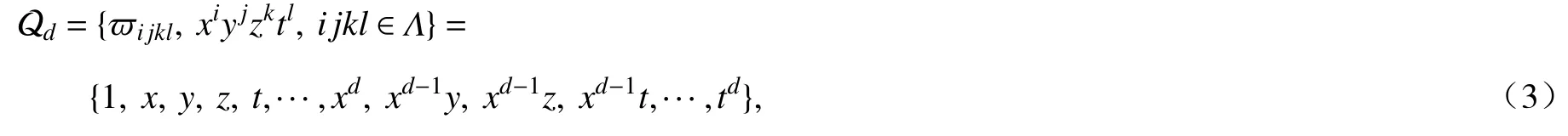
其中 Λ={0≤i+j+k+l≤d}.

空间 Qd中，线性无关的基函数个数为(d+1)(d+2)(d+3)(d+4)/24.假设方程(2)的解h(x,t)可以写为特解 χijkl(x,t)的一个线性组合：

其中 ζijkl为待求解系数，特解 χijkl(x,t)满足

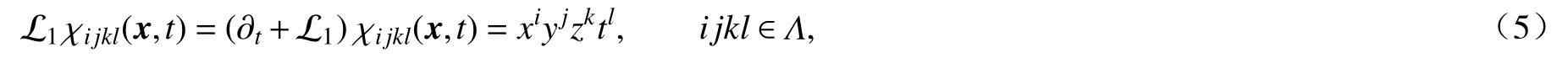
L1为L 中的空间常系数线性算子部分.在四维空间中，关于二阶线性常系数偏微分方程的特解 χijkl(x,t)有以下引理.

引理1[21]令(ω1,ω2,ω3,ω4)=(x,y,z,t)，则对于下列偏微分方程

为式(6)的一个多项式特解，其中d=i+j+k+l,L=

在区域 Ω 内部任取ni个配点，边界 ∂ Ω×(0,τ)上任取nd1个配点，边界Ω ×{t=0} 上任取nd2个配点，配点总数目为N=ni+nd1+nd2，则方程(2)的配点型强格式为

迭代求解代数方程组(8)，可得到待定系数{ζijkl|Λ}.将{ζijkl|Λ}代入式(4)即得到方程(2)的近似解.

为了比较说明多项式特解法的优点，假设方程(2)的解h(x,t) 可表示为多项式基函数ϖijkl(x,t)=xiyjzktl的一个线性组合：

其中 ςijkl为待定系数.将(x,t) 代入方程(2)，且在区域 Ω 内部任取ni个配点，边界 ∂ Ω×(0,τ)上任取nd1个配点，边界Ω×{t=0}上任取nd2个配点，配点总数目为N=ni+nd1+nd2，则方程(2)的配点型强格式为

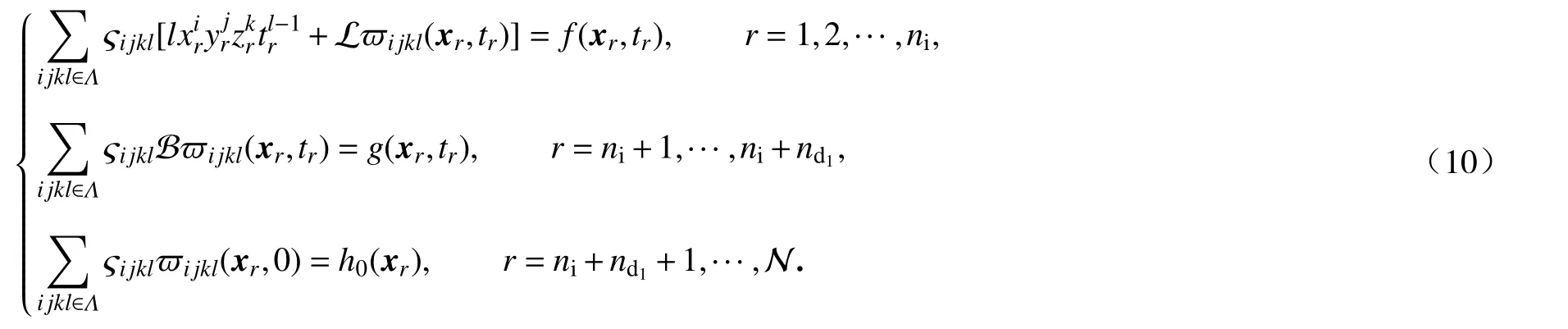
迭代求解代数方程组(10)，得到待定系数{ςijkl|Λ}.将{ςijkl|Λ}代入式(9)即得到方程(2)的近似解.

注3为使代数方程组(8)和(10)可解，配点的数目N 需大于完全多项式空间 Qd的维数(d+1)(d+2)(d+3)(d+4)/24.

本文的计算区域为规则区域和不规则区域，所用配点有两种方式：一是内点和边界点均为规则配点，二是内点和边界点均为随机配点.以二维区域为例，图1(a)、1(b)所示的是规则配点，图 1(c)、1(d)所示的是随机配点.二维非规则空间区域在新的三维时空域中随机取点如图2所示，规则二维空间区域在新的三维时空域中随机取点类似.

图1 配点图：(a) 正方形区域规则取点；(b) 星形区域规则取点；(c) 正方形区域随机取点；(d) 星形区域随机取点(篮圈：内点；红星：边界点)Fig.1 The collocation point diagram: (a) the regular domain with regular points; (b) the irregular domain with regular points; (c) the regular domain with random points; (d) the irregular domain with random points (blue circles: interior collocation points; red stars: boundary collocation points)

图2 时空区域中星形区域随机取点（篮圈：内点；红星：边界点）Fig.2 An irregular domain with random points in the space-time domain (blue circles: interior collocation points; red stars: boundary collocation points)

2 数值实验

数值解与精确解之间的平方根误差定义为

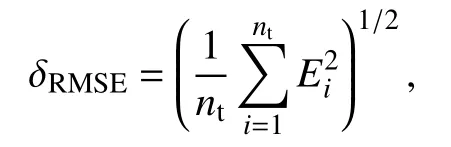
考虑下列三维Burgers 方程的初边值问题：

其中，µ=1/Re＞0为黏性系数，Re为Reynolds 数.方程(11)的精确解为

f(x,t),g(x,t)和h0(x)为基于精确解(12)的函数.

本文的研究区域为正方体区域和bumpy-shaped 型非规则区域，如图3所示.

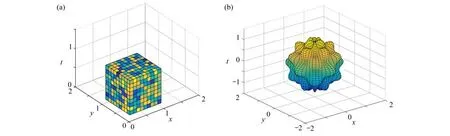
图3 空间求解区域：(a) 正方体区域；(b) bumpy-shaped 区域Fig.3 The spatial solution domains: (a) the cubic domain; (b) the bumpy-shaped domain

在数值实验中，我们将比较使用不同时刻 τ以及不同Reynolds数所得的数值模拟结果.如无特别说明，ni表示区域内部的配点数，nd表示边界∂Ω×(0,τ)∪Ω×{t=0} 上的配点数，nt表示测试点数.

2.1 大τ 情形

本小节的算例采用时空多项式配点法和直接使用多项式基函数时空配点法求解Reynolds 数Re=1时的方程(11).

表1给出了 τ=1，配点ni=3 819,nd=5 220,nt=1 919时，两种区域对不同阶多项式特解的计算时间和平方根误差.可以看出，随着特解阶的增加，平方根误差迅速下降；特解的阶越高，计算所需时间越长.同时，可以看出，立方体区域上的平方根误差下降得比bumpy 型区域上的平方根误差快.

表1 ni=3 819,nd=5 220,nt=1 919,τ=1时，两种区域多项式特解的平方根误差Table 1 The RMSE with ni=3 819,nd=5 220,nt=1 919,τ=1 for cubic and bumpy-shaped domains

表2给出了 τ=1，配点ni=3 819,nd=5 220,nt=1 919时，两种区域对不同阶多项式基函数的计算时间和平方根误差.可以看出，随着多项式阶的增加，平方根误差未有明显下降；多项式基函数的阶越高，计算所需时间越长.通过分析多项式基函数的系数矩阵，可以看到多尺度方法对其系数矩阵的条件数未有明显改进，这也是多项式基函数的平方根误差并不随着多项式基函数阶的增加而降低的原因之一.

表2 ni=3 819,nd=5 220,nt=1 919,τ=1时，两种区域多项式基函数的平方根误差Table 2 The RMSE with ni=3 819,nd=5 220,nt=1 919,τ=1 for cubic and bumpy-shaped domains

τ=2的数值结果如图4所示.易见，对这两种区域，当特解基函数的阶小于或等于12 时，所得计算结果的误差都以指数量级迅速下降.此后，再增加特解基函数的阶，所得计算结果的精度不再有显著提高，但也不会降低.当 τ=100时，两种区域的计算结果如图5所示.显然，当特解基函数的阶小于或等于12 时，所得计算结果都快速收敛.

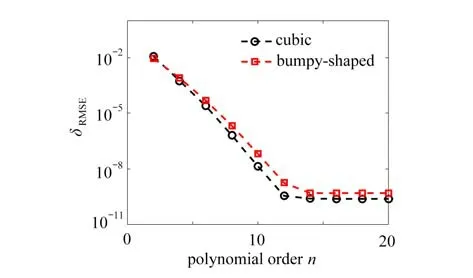
图4 τ=2,Re=1时，两种区域的计算结果Fig.4 Results for τ=2 andRe=1

图5 τ=100,Re=1时，两种区域的计算结果Fig.5 Results for τ=100 andRe=1

为进一步分析所得结果，τ=2时，正方体求解区域上的系数矩阵的条件数如图 6(a)所示.显然，在多项式特解中，使用多尺度技巧与否，所得矩阵的条件数相差巨大.如果不使用多尺度技巧，其条件数随着多项式特解阶的增加迅速增大，很快便数值溢出：多项式特解的阶等于12 时，所得数值结果发散.多项式特解的阶等于20 时，条件数溢出.使用多尺度技巧，可以有效控制条件数的增长，获得稳定的解.因此，在多项式类的解法中，多尺度技巧的使用是至关重要的.Bumpy-shaped 区域上条件数的情形与正方体求解区域上的情形类似.对于多项式基函数而言，系数矩阵的条件数使用和不使用多尺度技巧差别不大，如图 6(b)所示，这或许是直接使用多项式基函数所得的近似解精度不高的原因之一.

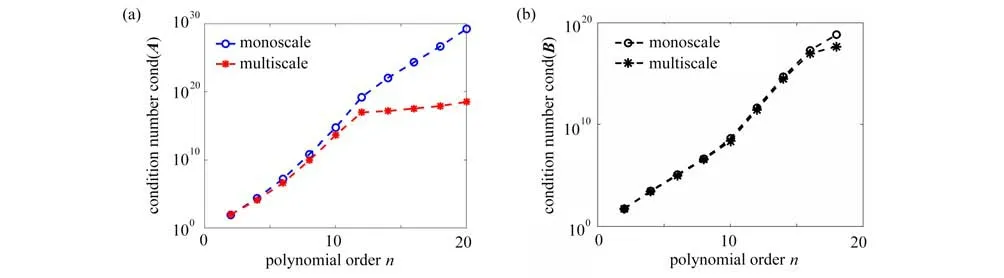
图6 τ=2时，正方体区域上系数矩阵的条件数：(a) 多项式特解系数矩阵的条件数；(b) 多项式基函数系数矩阵的条件数Fig.6 Matrix condition numbers of the cubic domain for τ=2: (a) the condition number of polynomial particular solutions; (b) the condition number of polynomial basis functions

根据本小节数值例子，可得下列结论.

1） 对于规则或不规则的计算区域，采用不同数目的配点，计算结果会有所不同，但是这些结果之间的差别很小，不足以影响到计算精度.

2） 采用不同数目配点的最大的区别在于计算时间，配点越多，所需的计算时间也越长.以正方体区域为例，ni=6 500，nd=6 000，nt=256时 所需的计算时间约为8 930 s.如果ni增加到10 000，nd增加到8 128，nt保持不变，则所需的计算时间增加4 529 s.由此可见，配点数目严重影响计算时间.在保证近似解精度的情况下，应选用适当数目的配点.对于非规则区域，其情形与正方体区域的情形类似，此处不再赘述.

3） 本算法中的多项式特解基函数 χijkl需要提前生成.生成1 阶到30 阶的多项式特解，所需总时间约为10 415 s.值得庆幸的是，特解基函数 χijkl一旦生成便可重复使用，甚至对于不同的微分方程，只要其中的线性微分算子项相同，也可使用.

2.2 不同Reynolds 数的情形

本小节中所有算例的τ均取1.在求解Burgers 方程时，的取值对所求数值解的精度影响巨大.现有研究结果表明，Reynolds 数Re越大，所得数值解的精度越低，求解难度越大.

当 µ=1，所得结果如图7所示.正方体区域上数值解的精度达到10-11，即使在非规则区域bumpy-shaped上，数值解的精度仍然能达到10-9.当µ=0.5时，所得结果如图8所示.正方体区域上数值解的精度达到10-8，非规则区域bumpy-shaped 上数值解的精度约为1 0-6.继续增大Reynolds 数，µ=0.1，正方体区域上数值解的精度达到10-5，而非规则区域bumpy-shaped 上数值解的精度约为1 0-3，且数值解不再像 µ=1时那样光滑.因此，本文数值结果进一步验证了Reynolds 数越大，所得数值解的精度越低，求解难度越大，这与以往的研究结果一致.

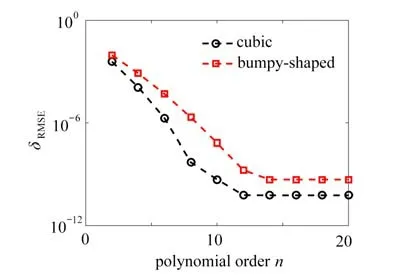
图7 τ=1,µ=1时，两种区域的计算结果Fig.7 Results for τ=1 andµ=1

图8 τ=1,µ=0.5时，两种区域的计算结果Fig.8 Results for τ=1 andµ=0.5

表3给出了 τ=1，配点ni=3 819,nd=5 220,nt=1 919,µ=0.5时，两种区域直接使用多项式基函数的计算时间和平方根误差.可以看出，随着多项式基函数阶的增加，平方根误差几乎没有降低.

表3 ni=3 819,nd=5 220,nt=1 919,µ=0.5时，两种区域多项式基函数的平方根误差和计算所需时间Table 3 The RMSE with ni=3 819,nd=5 220,nt=1 919,µ=0.5 for cubic and bumpy-shaped domains

3 结 论

三维Burgers 方程因其维数高，大Reynolds 数时的强非线性性，现有研究结果不多.本文提出了一种新型时空多项式特解配点法求解三维Burgers 方程，不同于以往的多项式函数直接做基函数的方法，多项式特解做基函数的优点是对控制方程中的线性导数项不进行求导，因此多项式特解的阶比较高时，所得系数矩阵中元素的量级差别不大，从而算法的稳定性强，精度很高.采用配点法时，时空方法的维数比初始问题的维数增加了一维，所需配点数目较多，下一步的工作可以通过采取有效的降阶技巧减少对配点的要求，将系数矩阵变为稀疏矩阵，以期得到更好的模拟结果.通过本文的工作，使学生对高维强非线性的Burgers 方程的数值求解有更加深入的理解.