基于LiToSim平台的疲劳寿命评估LtsFatigue软件开发及应用*

彭梦瑶，顾水涛，周洋靖，王世猛，冯志强,3

（1.重庆大学 土木工程学院，重庆 400040；2.重庆励颐拓软件有限公司，重庆 401121；3.西南交通大学 力学与航空航天学院，成都 610031）

（我刊编委冯志强来稿）

引 言

工程结构在循环荷载作用下，其失效模式主要为疲劳破坏.结构疲劳破坏所受到的交变应力虽尚未达到材料屈服强度，但却可能有瞬发性的断裂问题，存在着巨大的安全隐患.而应用疲劳耐久性技术，可避免50%的疲劳断裂问题，因此许多企业将疲劳耐久性定为产品质量控制的重要指标[1].

在实际应用中，汽车、飞行器及其他机械结构，大多在随机荷载作用下工作.国内外诸多学者对其随机疲劳问题展开了深入研究，主要工作有以下几个部分：结构疲劳强度理论，包括常规疲劳强度设计、基于断裂力学的疲劳强度设计、基于可靠性理论的疲劳强度设计[2]；随机载荷的统计方法，随机载荷不规则且无法重复，对随机载荷只能进行统计描述，包括计数法和功率谱法两种[3-4]；疲劳损伤累积理论，包括线性损伤累积理论和非线性损伤累积理论[5-6].目前可将随机疲劳的分析方法归为两类：第一类是基于随机过程的时间历程曲线进行循环计数的时域法，第二类是利用随机过程的功率谱密度(power spectral density,PSD)函数估算的频域法.

对于时域法而言，疲劳损伤需要基于瞬态分析计算的动力响应进行时程计算.对其随机载荷的统计，相应的计算方法包括峰值计数法、界限计数法、幅值平均计数法以及雨流计数法[7-9].其中雨流计数法具有良好的计算精度，被认为是疲劳损伤分析结果好坏的基准[10].然而，时域法的疲劳计算精度常常受到时距模拟时间长短的影响，只有通过足够长的样本时距以减小时域模拟中的误差.对于复杂结构，样本时距的增加将会大大提高计算时间[11-12].就其计算效率而言，时域法不能够满足工程实际需求.

尽管时域法计算结果准确，但其计算成本较大且计算精度受到样本时距的影响.与时域法相比，频域法通过疲劳危险点位置的应力响应PSD 计算随机载荷引起的疲劳损伤，能够有效减少计算工作量，是设计人员预测结构疲劳损伤的较好选择.但是，频域法的计算精度依赖于经验公式的准确性，现有经验方法包括：窄带法、Dirlik 疲劳损伤公式、Z-B 法疲劳损伤公式、T-B 法疲劳损伤公式等[13-17].若能选择适当的频域计算公式使得疲劳计算精度满足要求，则可以避免时域法的计算效率缺陷，因此频域法具有良好的应用前景.

随着计算机技术和有限元技术的发展[18]，国内外出现了多款疲劳分析软件，如Fe-Fatigue（英国）、Fesafe（英国）、MSC-Fatigue（美国）、Ncode（英国）、WinLIFE（德国）、ProEMFAT（中国）等系列软件.上述软件功能强大，但随机载荷的频域算法尚不完善，除了Ncode、Fe-safe 可进行频域疲劳分析的工作外，其余软件暂未发展这方面的功能.为此，本文以开发定制化疲劳软件LtsFatigue为目标，基于国内自主CAE 软件开发平台LiToSim，嵌入随机疲劳数值分析程序，集成疲劳时域算法、频域算法到有限元计算框架中，形成一套完整的疲劳求解计算程序，弥补了频域算法在常见疲劳软件中的空缺，同时利用LiToSim 强大的前后处理开发接口，可实现用户界面友好、可视化效果丰富、随机疲劳问题高效处理的定制化疲劳软件LstFatigue的开发.

1 疲劳损伤及寿命预测理论基础

1.1 时域法疲劳分析

结构疲劳是指结构在循环荷载作用下裂纹形成与扩展的过程.时域法通过结构动力计算得到疲劳危险点位置的应力响应时程，进而使用时域雨流计数法对时程数据处理得到危险点处的应力循环特性，包括应力循环幅值和每个幅值所对应的循环均值、循环次数.雨流计数法详见文献[9].

通过雨流计数法获得的结果与材料S-N(stress-life) 曲线公式相结合，可实现结构疲劳寿命预测.S-N曲线通常由大量实验数据拟合得到，其中常用的幂次表达式如式(1)所示，C，k均为材料参数.若构件在等幅应力S作用下，循环至破坏疲劳寿命N：

由于实验得到的S-N曲线往往是通过零均值加载得到的，因此雨流计数法统计得到的应力循环特性需要考虑平均应力的影响[19]，可采用Goodman/Gerber 等方法修正：

式中，Sm表示实际应力循环应力均值，Su表示极限强度，Sa表示实际应力循环幅值，Sa(-1)表示零应力均值的等效循环幅值且应用于S-N曲线进行疲劳寿命估算.当p=1时，式(2)为G oodman 修正公式；当p=2时，式(2)为Gerber修正公式.

疲劳损伤通常采用Miner 线性损伤累积准则计算.结构在变幅应力Si作用ni次循环下的损伤为di，若在l个应力幅值Si作用下各经历ni次循环，则其疲劳总损伤D为

结构疲劳寿命Nf指结构在疲劳破坏前所经历的应力循环次数，变幅加载的随机疲劳可根据累积疲劳损伤计算.由于结构在非危险点位置的疲劳寿命数值较大（10的幂次方），为简化显示结果，以10为底的对数形式l gNf表示：

时域法采用雨流计数对时程曲线进行准确计数，计算精度高.但时域法依赖于样本时距的长短，由于雨流计数法需要对每个数据进行处理，样本时距将对计算效率产生影响.对工程实际结构进行疲劳分析，需要在满足计算精度要求的同时有效提高计算效率[10].

1.2 频域法疲劳分析

频域法通过随机振动理论获得结构疲劳破坏控制点处的应力响应PSD，利用频谱参数等确定应力循环分布的概率密度函数，依据S-N曲线及Miner 线性损伤累积准则及经验公式来估算疲劳损伤，其核心在于估算应力幅值的概率密度函数.由Miner 线性准则和应力幅值的概率密度间的关系，可将疲劳损伤的期望率E(D)表示为[20]

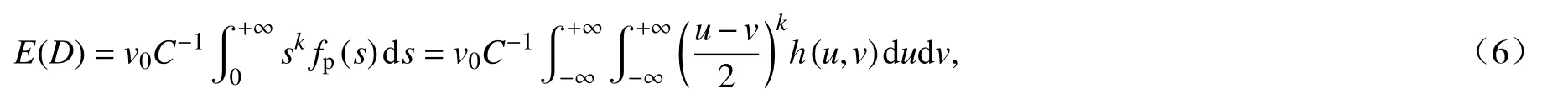
式中，穿零率v0为单位时间的循环总数；C，k为S-N曲线材料参数；s表示应力幅值；fp(s)为其概率密度函数；u，v分别为峰值和谷值，h(u,v)为其联合概率密度.

疲劳总损伤D可由疲劳损伤的期望率E(D)表示为

式中，T为样本时距；E(D)为疲劳损伤期望率，即单位时间疲劳损伤.频域法结构疲劳寿命及寿命对数可由式(7)与式(4)、式(5)联立求解得到.

由于应力循环的响应统计特性不同，可依据带宽参数（α1，α2）和统计参数（均值Sm、标准差σX、偏度Sk、峰度Ku）将随机过程分为窄带Gauss 随机过程、宽带Gauss 随机过程、非Gauss 随机过程[21].

1.2.1 窄带Gauss 随机过程

窄带Gauss 随机过程应力幅值s的概率密度函数fp(s)近似服从Rayleigh 分布：

式中，σ2X为随机过程的方差.

1.2.2 宽带Gauss 随机过程

宽带Gauss 随机过程计算疲劳损伤的应力幅值概率密度函数较复杂，若仍采用窄带Gauss 过程的Rayleigh 分布假设，将会高估疲劳损伤率，需要找出更合理的应力幅值（或范围）概率密度函数[22].T-B 谱方法提出一种线性组合近似计算：

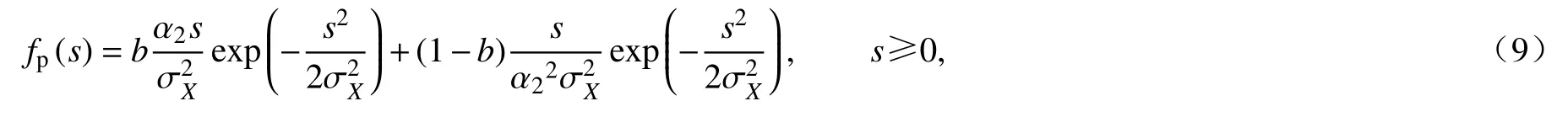
其中，b为组合参数，α1，α2是由谱矩表示的带宽参数，且1＞α1＞α2＞0，当α1=α2=0 时为白噪声，α1=α2=1时为严格的窄带随机过程.参数b的选择主要通过大量模拟实验拟合得到.文献[17]提出b可由带宽系数 α1和α2表示为

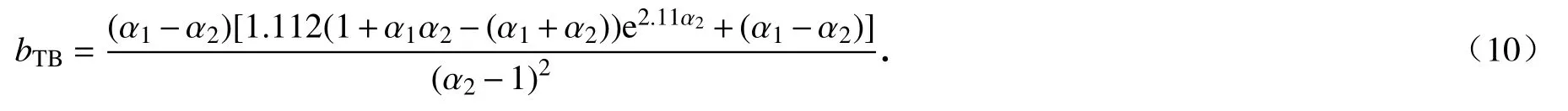
Ding 和Chen[23]基于T-B 法改进为D-C 谱方法，通过数据拟合的方式给出了更简化的参数b的形式：

参数b与响应谱形状相关，选择不同经验公式将直接影响频域疲劳分析的计算精度.

1.2.3 非Gauss 随机过程

式中，hGRF(xu,xv)为Gauss 过程中的雨流计数法所得峰值谷值概率分布函数，同时可表示为

其中，hGLC(xu,xv)为界限计数法(LC 法) 计算得到的峰值谷值联合概率密度函数，hGRM(xu,xv)为范围计数法(RM 法)计算得到的峰值谷值联合概率密度函数[23]：

结构疲劳分析流程如图1所示.

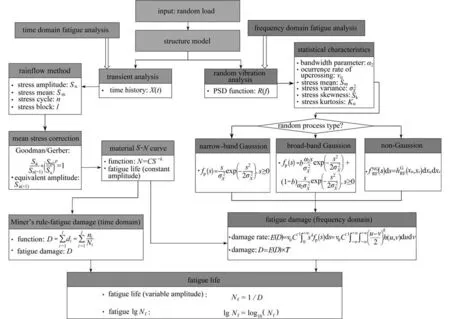
图1 结构疲劳分析流程Fig.1 The structural fatigue analysis process

2 LtsFatigue 疲劳分析软件构建

基于LiToSim 平台，嵌入含时域、频域算法的疲劳分析数值计算程序，定制化开发一款LtsFatigue 疲劳软件.

2.1 LiToSim 平台简介

LiToSim是一款采用C++语言、面向对象编程思想及通用数据标准研发的有限元软件共性开发平台.具有数据处理、图形交互和项目管理等诸多功能，能够为用户高效地开发专用CAE 软件提供支持[18].

LiToSim 定制化层包括专业模块和专业软件求解器两部分[24].专业模块提供专业的CAE 软件开发所需的前/后处理功能模块及相关接口；专业软件求解器提供常规问题通用求解器和特定问题相关定制求解器接口[25-28].LiToSim 平台架构如图2所示.

图2 LiToSim 平台架构图Fig.2 The LiToSim platform architecture diagram

2.2 LtsFatigue 疲劳软件组织结构

基于LiToSim 已有的通用前处理、求解器模块及其开放接口，定制化开发疲劳分析软件LtsFatigue.如图3所示，疲劳分析所需新增的模块包括计算模型、材料参数及疲劳算法模块三个部分，同时新增针对疲劳分析的后处理结果显示.

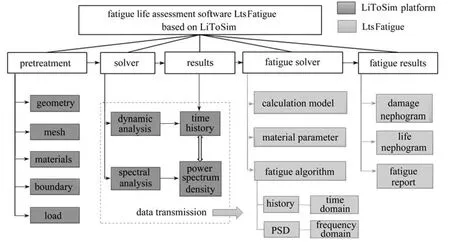
图3 基于LiToSim的定制化疲劳软件LtsFatigue 组织结构图Fig.3 The organizational structure of the LiToSim software fatigue module (LtsFatigue)

针对疲劳各子模块的功能应用，设计LtsFatigue 软件的界面便于用户操作.如图4所示，界面可主要分为三个部分，包括计算模型、材料参数、疲劳算法及结果后处理模块.

图4 基于LiToSim的定制化疲劳软件LtsFatigue 界面Fig.4 The interface for customized software LtsFatigue based on LiToSim

2.2.1 计算模型模块

LtsFatigue 软件与LiToSim 有限元分析软件直接连接集成，依赖于有限元软件的计算结果.在LiToSim 软件完成结构动力计算后，通过界面操作导入模型整体或表面的节点、单元网格信息及其应力响应结果，同时选择载荷类型为时程序列或PSD.

2.2.2 材料参数模块

LtsFatigue 软件的材料库提供常用钢材、铝合金的疲劳性能数据，主要包括一般材料数据信息如弹性模量E、Poisson 比v、S-N曲线、E-N曲线、疲劳强度指数b、疲劳强度系数sf等数据.用户在如图5所示的主界面材料模块点击按钮，可对这些数据进行自定义编辑、图形绘制等操作.

2.2.3 疲劳算法模块

对于导入应力响应时间历程结果的疲劳计算，提供基于应力-寿命的时域疲劳算法.对于导入应力响应PSD 函数的疲劳计算，提供基于应力-寿命的频域疲劳算法.

此外，该模块提供多种平均应力修正方法，包括Goodman、Gerber 等修正公式.其中，时域法对雨流计数法计算得到的多个应力循环逐一进行平均应力修正，频域法对应力响应PSD 函数的整体平均应力进行修正.

2.2.4 疲劳结果后处理模块

LtsFatigue 后处理模块可分别对节点、单元的计算结果绘制疲劳损伤、疲劳寿命云图等，同时用户可在图6所示的界面中选择几何表面、几何体、边缘单元等多种方式查阅疲劳分析结果.

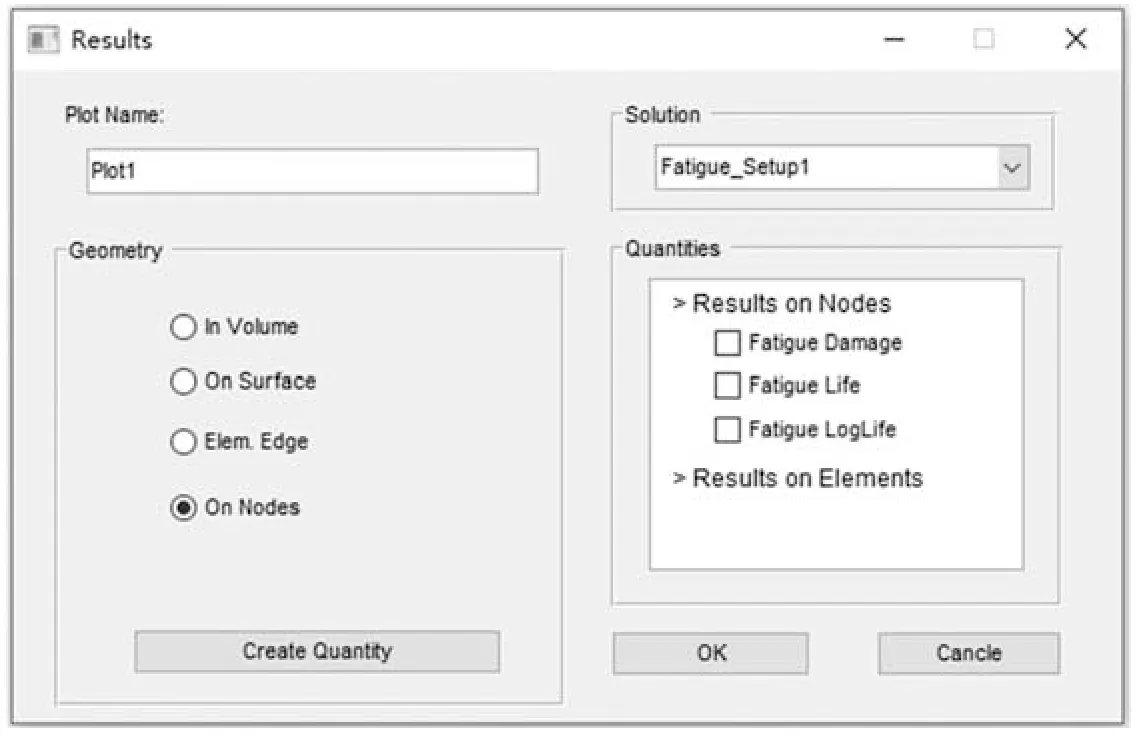
图6 疲劳结果绘制Fig.6 The fatigue results plot

2.3 LtsFatigue 疲劳分析操作流程

LtsFatigue 疲劳软件依赖于有限元分析结果，需要先通过LiToSim 完成结构模型的建立、材料参数的定义、边界条件的设置、结构网格划分等流程，并进行结构动力计算输出应力响应数据.然后在LtsFatigue 疲劳软件界面中的计算模型模块提取有限元结果，材料模块定义材料参数，疲劳算法模块选择疲劳算法及平均应力修正公式.通过LtsFatigue 界面操作完成上述设置，进行疲劳分析计算，其界面图见图4、流程图见图7.

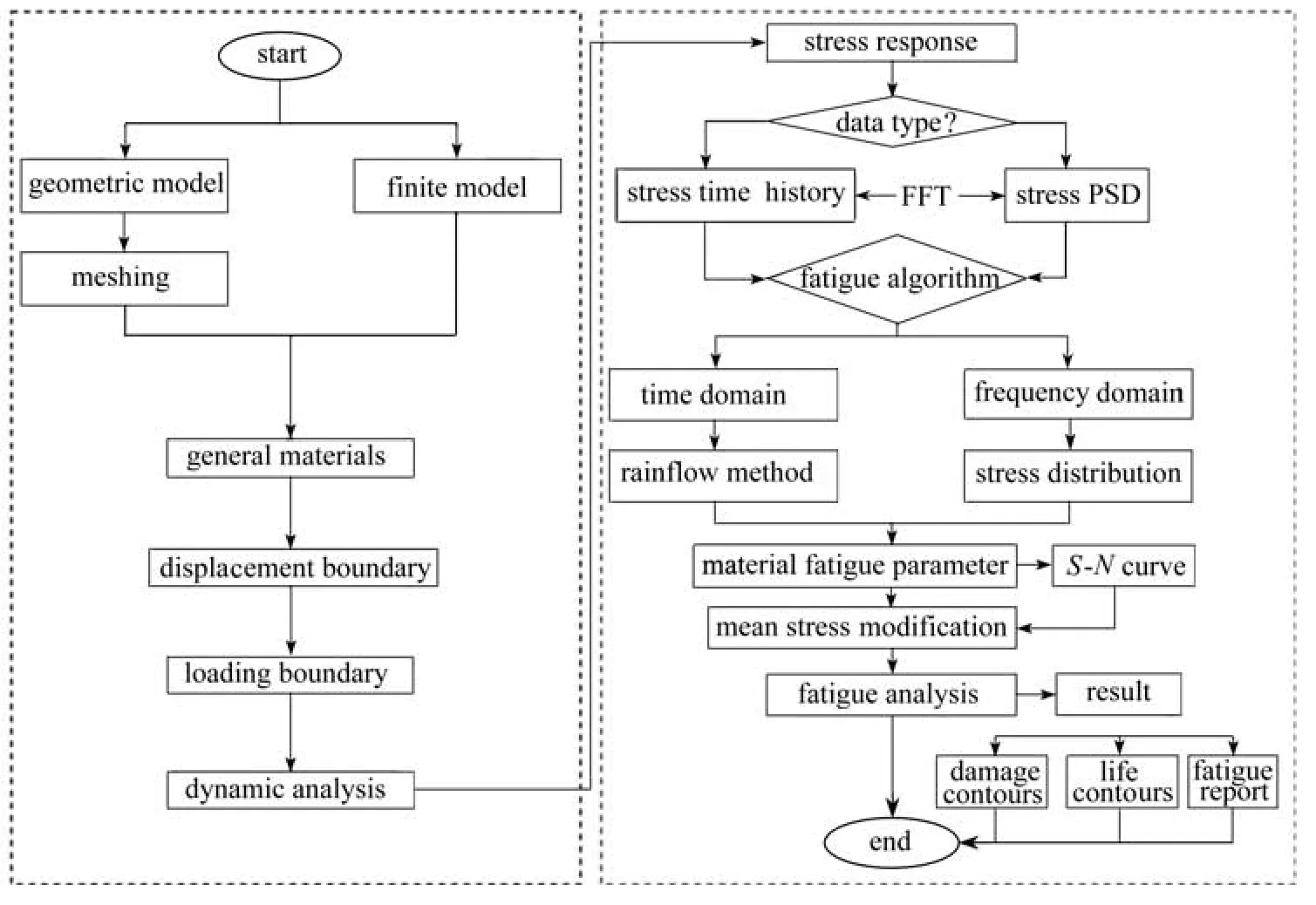
图7 基于LiToSim的定制化疲劳软件LtsFatigue 分析流程Fig.7 The analysis process of customized software LtsFatigue based on LiToSim

3 LtsFatigue 软件数值算例

齿轮构件应用广泛，其疲劳问题突出.本文以齿轮构件为例，钢材选择Q345 钢，屈服强度345 MPa，极限拉伸强度500 MPa.

几何参数：齿数为20，模数为2.75，如图8所示.材料特性：弹性模量为2.1×105MPa，Poisson 比为0.33.疲劳参数：疲劳强度系数sf=600 MPa，疲劳强度指数b=-0.095，材料S-N曲线（S为应力幅值，N为S幅值循环的疲劳寿命）公式满足

图8 齿轮示意图Fig.8 Schematic diagram of the gear

边界条件：齿轮中心圆孔固定约束，圆环表面受到随机载荷.

为探究自主开发的疲劳软件LtsFatigue的计算优越性，对齿轮算例进行疲劳分析，以大型商业软件ABAQUS联合Fe-safe 计算结果为基准，从疲劳计算精度、计算效率两方面探究LtsFatigue 软件所具有的优势.

齿轮受到的疲劳荷载为一组样本时距长度4 000 s的随机载荷，采样频率10 Hz.最后载荷步的有限元计算结果见图9，第一主应力最大的节点9018(14 mm,-6.93 mm,0.99 mm)，所在位置被认为是疲劳危险点之一.国内自主CAE 软件LiToSim的有限元分析结果与商业软件ABAQUS 计算结果一致，这说明定制化疲劳软件LtsFatigue 基于LiToSim 平台进行开发可靠有效.

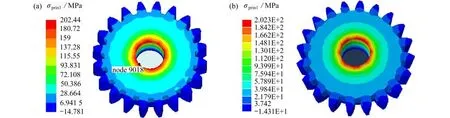
图9 有限元分析结果，第一主应力对比：（a） LiToSim 有限元分析结果，第一主应力；（b） ABAQUS 有限元结果分析结果，第一主应力Fig.9 For finite element analysis (FEA) results,the comparison of the 1st principal stress: (a) LiToSim FEA results; (b) ABAQUS FEA results

疲劳危险位置节点9 018的应力响应时程曲线见图10，该组数据的统计特性如表1所示，该点的应力响应时程为弱非Gauss 宽带随机过程，其疲劳分析在时域可采用雨流计数法，在频域可选用D-C 谱方法估算齿轮结构的疲劳寿命.

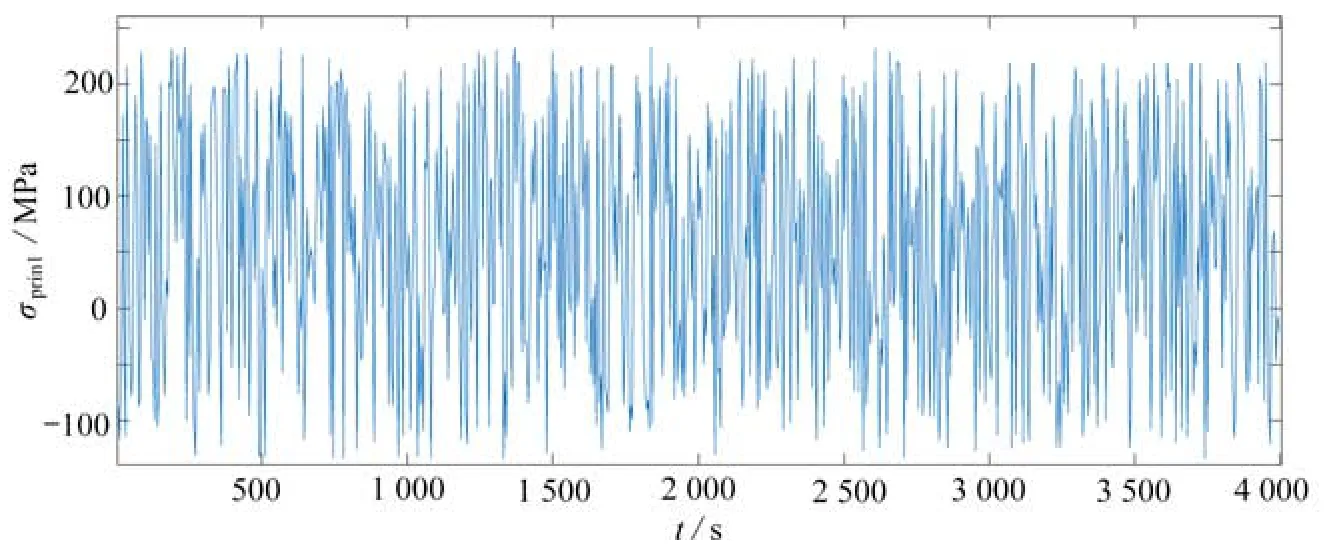
图10 节点9 018 应力响应时程曲线Fig.10 The time-history curve of stress response at node 9 018

表1 应力响应统计特性Table 1 Stress response statistical characteristics

3.1 算例1：时域法疲劳分析

对于时域疲劳分析，采用雨流计数法对应力响应准确计数.LtsFatigue 软件计算的齿轮构件疲劳损伤、疲劳寿命云图见图11(a)，Fe-safe 联合ABAQUS 软件计算的疲劳寿命云图见图11(b).对比结果可知，Fe-safe 计算得到的齿轮最危险位置的疲劳寿命（l gNf）为0.934 3，LtsFatigue 计算得到的疲劳寿命（l gNf）为0.938 1，结果相差约1%，软件计算精度满足要求.

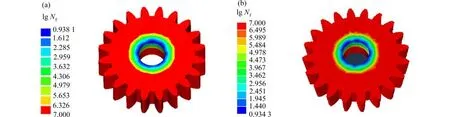
图11 LtsFatigue 与Fe-safe 时域疲劳寿命对比：（a） LtsFatigue 疲劳寿命结果，时域法；（b） Fe-safe 疲劳寿命结果，时域法Fig.11 Comparison of the fatigue life between LtsFatigue and ABAQUS/Fe-safe time domain: (a) the LtsFatigue fatigue life-time domain;(b) the Fe-safe fatigue life-time domain

3.2 算例2：频域法疲劳分析

对于频域疲劳分析，采用应力循环分析函数的经验公式估算疲劳损伤，可通过Fourier 变换将应力响应时程转换为PSD.以LtsFatigue 内置D-C 谱方法为例，将时域疲劳结果作为基准，验证频域算法的准确性.从LtsFatigue 疲劳寿命云图（图12(a)为时域结果，图12(b)为频域结果）对比来看，频域算法计算结果与时域结果相差约3%，计算精度基本满足要求.同时，表2结果表明LtsFatigue 应用频域算法估算疲劳寿命，计算效率提高约45%.分析其原因在于频域法通过概率分布函数替代了时域法中雨流计数法对随机过程的处理，使得疲劳分析过程有效简化.频域法与时域法二者精度相当，但频域法在效率上有明显优势，因此对于复杂结构的随机疲劳分析问题，应用频域疲劳算法具有重要意义.

表2 LtsFatigue 与Fe-safe 计算精度和计算效率对比Table 2 Comparison of computational accuracy and computational efficiency between LtsFatigue and Fe-safe

图12 LtsFatigue 时域与频域疲劳寿命：（a） 时域法；（b） 频域法Fig.12 LtsFatigue time domain and frequency domain fatigue lives: (a) the fatigue life-time domain; (b) the fatigue life-frequency domain

4 结 论

本文将基于应力时间历程的时域疲劳算法与基于应力PSD的频域疲劳算法嵌入有限元分析框架，充分利用LiToSim 平台的开放接口，形成了一款疲劳分析定制化软件LtsFatigue.通过对齿轮算例疲劳分析，验证了LiToSim 平台有限元分析结果的可靠性，对比了定制化软件LtsFatigue的时域算法、频域算法计算精度与大型商业软件ABAQUS 联合Fe-safe 结果相差约3%，同时频域算法将计算效率提高约45%.针对复杂结构的疲劳模拟分析，在保证计算精度的前提下，频域算法是提高计算效率的重要工具.基于LiToSim 平台的疲劳分析定制化软件LtsFatigue，为国内自主研发软件提供了一条新思路.