有界多连通区域数值保角变换的GMRES(m)法*

伍 康，吕毅斌，石允龙，王樱子

（1.昆明理工大学 理学院，昆明 650500；2.昆明理工大学 计算中心，昆明 650500）

引 言

保角变换是复变函数论中的经典课题，可应用于流体力学、电磁理论、热传输和图像处理等，在计算复杂截面形状的某些物理量中发挥着重要作用[1-5].保角变换的主要求解方法有解析法和数值法.解析法局限于只能在部分特殊的区域给出具体的变换函数表达式，而数值法能通过算法设计很好地逼近变换函数.因此，对于那些更具一般性的实际问题，必须通过数值法计算变换函数.计算保角变换的主要数值法有积分方程法、正交多项式法、有理逼近法以及有限差分法等[6-10].20世纪80年代以来，Amano 提出了基于模拟电荷法的数值保角变换计算法，用于计算将任意单连通区域内部或外部映射到单位圆内部或外部，双连通区域映射到圆环以及多连通区域映射到部分正则狭缝域的保角变换函数[11-12].

多连通区域能通过保角变换映射到五种正则狭缝域：带同心圆弧狭缝的圆环S(a)、带同心圆弧狭缝的圆盘S(d)、同心圆弧狭缝域S(c)、径向狭缝域S(r)和平行狭缝域S(p,θ)，θ是狭缝与水平正半轴的夹角，参见图1[13].Okano 和Ogata 等成功地将有界多连通区域保角映射到了有界狭缝域S(a)和S(d)，但没有给出将有界多连通区域映射到无界狭缝域S(c)，S(r)和S(p,θ)的保角变换函数形式[14].在上述研究的基础上，本文研究了将有界多连通区域映射到无界狭缝域S(c)，S(r)和S(p,θ)的保角变换函数形式，补充了基于模拟电荷法的数值保角变换计算法的理论内容，同时推广了文献[15]的结果.本文的方法首先是将求解映射函数的问题转化为通过模拟电荷法求解一对定义在问题区域D上的共轭调和函数g(z)和h(z)，这对共轭调和函数在D的边界 ∂D上满足Dirichlet 边界条件.在求解调和函数过程中使用复对数的线性组合近似g(z)，通过代入约束点和模拟电荷点得到约束方程，再用GMRES(m)法求解约束方程得到模拟电荷，获得了高精度的近似保角变换函数，并用最大模原理进行误差评价.提出了将有界多连通区域映射到S(c)，S(r)和S(p,θ)的数值保角变换的GMRES(m)法.

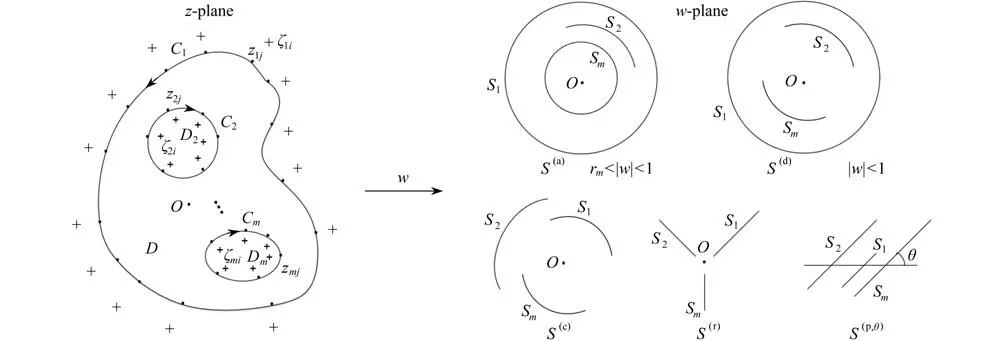
图1 基于模拟电荷法的有界多连通区域保角变换(“·”代表约束点，“+” 代表模拟电荷点)Fig.1 The conformal mapping of bounded multi-connected regions based on the charge simulation method(“·” represents collocation points,“+” represents charge points)

本文的组织结构如下：第1 节给出了有界多连通区域映射为无界狭缝域S(c)，S(r)和S(p,θ)的保角变换函数形式和g(z)+ih(z)的近似形式，并根据边界条件构造出约束方程.第2 节提出利用GMRES(m) 法计算约束方程.第3 节通过典型的数值实验验证了算法的有效性，结果显示得到精度更高的变换函数.第4 节给出了本文的结论与展望.

1 有界多连通区域映射到S(c),S(r)和S(p,θ)的数值保角变换

在z平面上，有界多连通区域D，是一个连通度为m(≥1)的区域，其边界 ∂D由m条封闭的Jordan 曲线C1,C2,···,Cm组成，区域D2,···,Dm在C1的内部是z平面内曲线C2,···,Cm围成的单连通区域.与有界狭缝域S(a)和S(d)不同，S(c)，S(r)和S(p,θ)是w平面上的无界狭缝域.保角变换函数w(z)将边界曲线C1,C2,···,Cm分别映射为狭缝S1,S2,···,Sm，将区域D映射为无界区域.

1.1 同心圆弧狭缝域S(c)

同心圆弧狭缝域S(c)由m条同心不同半径的圆弧狭缝Sl和整个w平面组成，Sl的半径为待确定的实数rl(l=1,2,···,m)，参见图1.当保角变换函数wc(z)满足正规化条件wc(u)=0，wc(v)=∞ 和Resz=v wc(z)=1(u,v∈D,u≠v)时(Res(·)表示取留数），可以表示如下[13]：

由Resz=v wc(z)=1，得g(v)+ih(v)=0，边界条件可以表示为

那么g(z)是满足Dirichlet 型场势问题

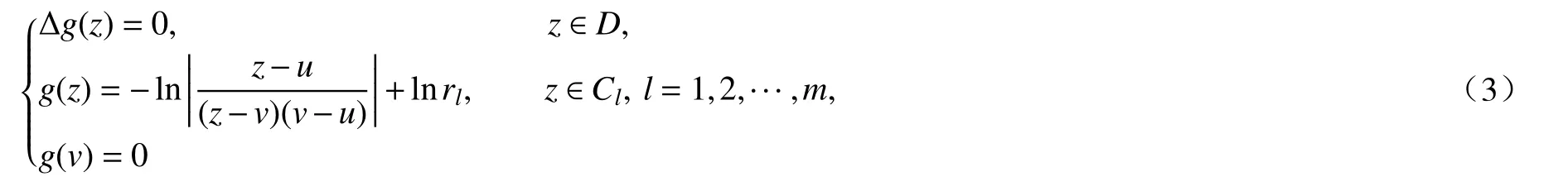
的解.

1.2 径向狭缝域S(r)

径向狭缝域S(r)由m条指向原点且与水平正半轴的夹角分别为待确定的实数rl的线段Sl(l=1,2,···,m)和整个w平面组成，参见图1.当保角变换函数wr(z)满足正规化条件wr(u)=0，wr(v)=∞ 和Resz=v wr(z)=1(u,v∈D,u≠v)时，可以表示如下[13]：

由Resz=v wr(z)=1，同样可得g(v)+ih(v)=0，边界条件可以表示为

那么g(z)是满足Dirichlet 型场势问题

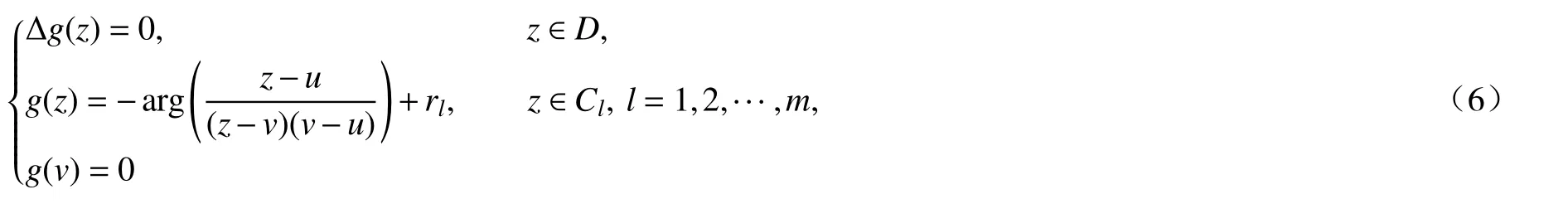
的解.

1.3 平行狭缝域S(p,θ)

平行狭缝域S(p,θ)由m条与水平正半轴的夹角为θ的平行线段Sl和整个w平面组成，Sl的位置由待确定的实数rl(l=1,2,···,m)决定，参见图1.当保角变换函数wp(z)满足正规化条件wp(v)=∞和 limz→v时，可以表示如下[13]：

由limz→v同样可得g(v)+ih(v)=0，边界条件可以表示为

那么g(z)是满足Dirichlet 型场势问题

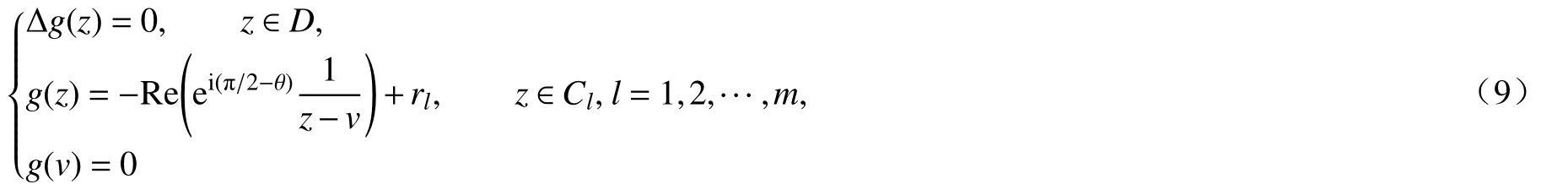
的解.

以上三种情况，h(z)与g(z)互为共轭调和函数，正规化条件都表示为g(v)+ih(v)=0，只有边界条件表示不同.以下用W,G,H,Rl分别表示w,g,h,rl的近似值.根据模拟电荷法的原理，g(z)和h(z)可以被一个复对数函数的线性组合近似，

这里，ζli是配置在曲线Cl(l=1,2,···,m;i=1,2,···,Nl) 外部的模拟电荷点，未知量Q0和 模拟电荷Qli分别为复常数和实数.为了实现上述三种类型的保角变换，该近似需要满足以下四个条件[14].

① 边界条件

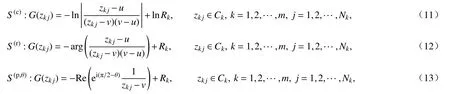
约束点zkj配置在边界Ck(k=1,2,···,m)上，并与模拟电荷点的数量相同.

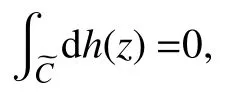
从而得

③ 根据文献[14]和[16]，该近似形式中的Qli还需满足

④ 正规化条件

根据式(16)，消去式(10)的Q0，得到近似形式：

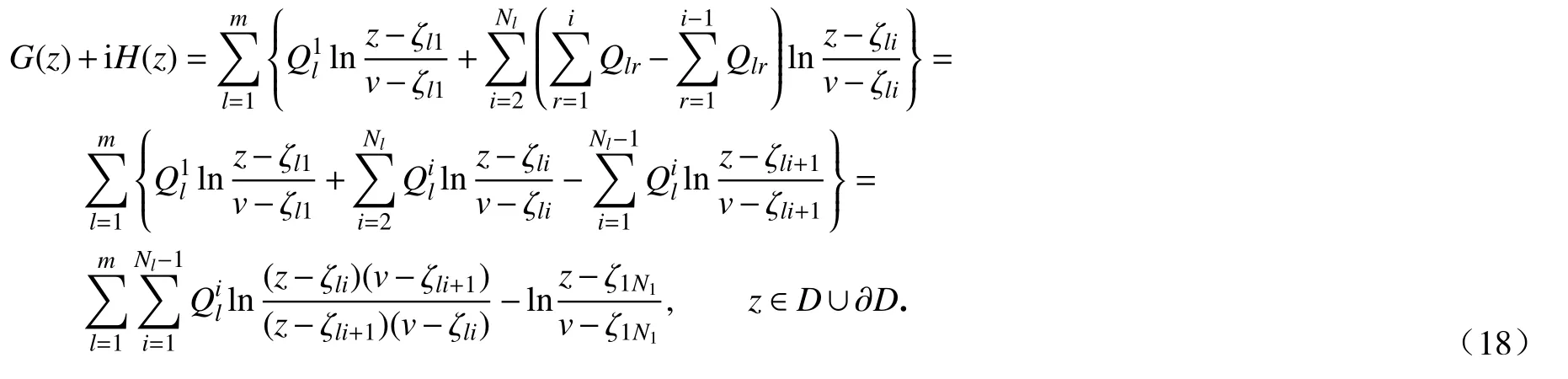
通过限制式(18)中z取Ck上的约束点zkj，并令其分别满足边界条件(11)～(13)，便可得到三种保角变换各自关于未知电荷Qil和Rk应该满足的约束方程，即

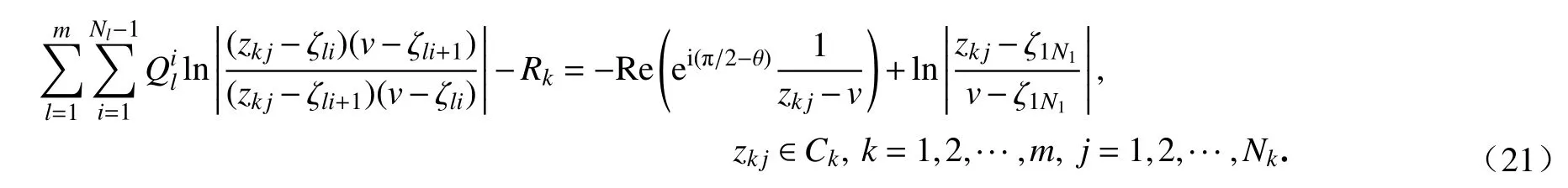
这些约束方程都构成N1+N2+···+Nm维的线性方程组，解出Qil后代入式(18)得到g(z)+ih(z)的近似，将其代入式(1)、(4)和(7)便可得到保角变换的近似函数.

2 求解模拟电荷的GMRES(m)法

随着电荷点数的增加，约束方程的系数矩阵的条件数会增大，这样的约束方程是病态的.现将约束方程(19)～(21)写成标准线性方程组Ax=b的形式，其中

A∈R(N1+N2+···+Nm)×(N1+N2+···+Nm),x∈RN1+N2+···+Nm,b∈RN1+N2+···+Nm,

A是非对称的.m步重启的广义极小残差法GMRES(m)是在Krylov 子空间

Km(A,r0)=span{r0,Ar0,···,Am-1r0}

讨论求解线性方程组的方法，可以直接应用于求解系数矩阵密集且不对称的大型线性方程组.它通过寻找近似解xm=x0+z来逼近线性方程组的准确解，其中z∈Km(A,r0)，并采用m步后必须重启的方式避免了计算过程中计算量和存储量过大的问题[17].其算法步骤如下：

算法1 模拟电荷的算法

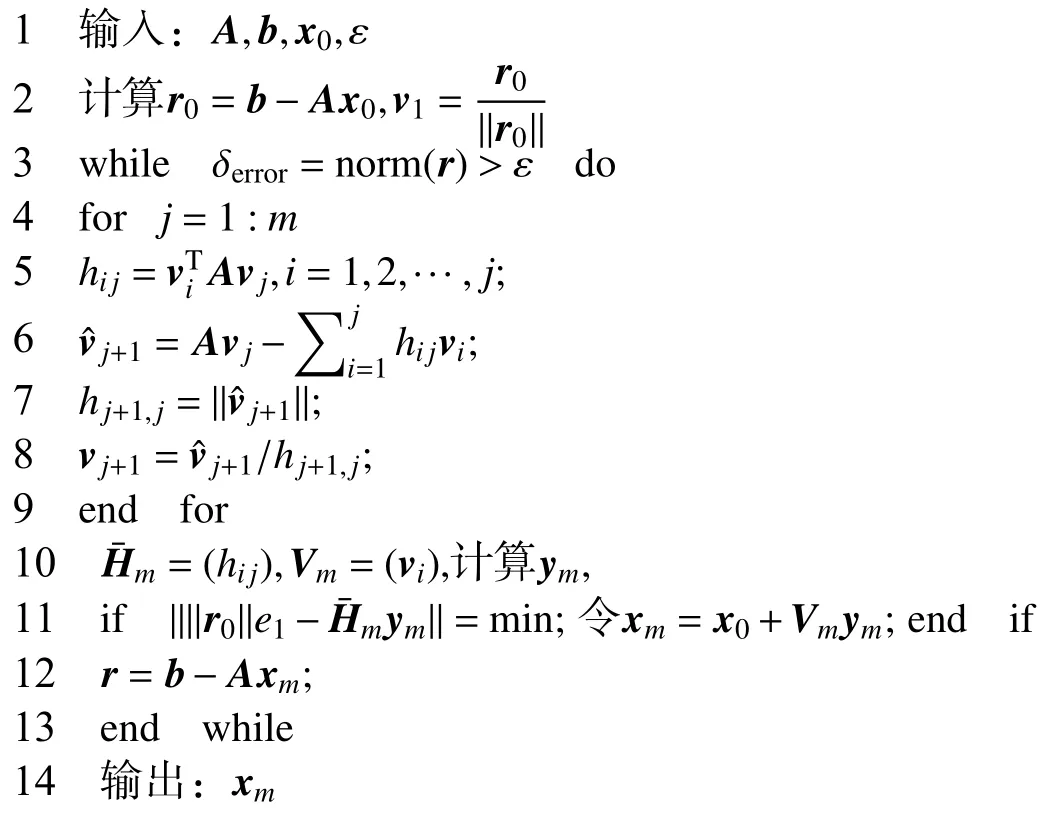
上述算法中，x0为给定的初始近似值，取为零向量，ε是允许的最大误差.

3 数值实验

在MATLAB 2018b的环境下，以三连通区域为例，参见图2，其边界曲线的方程为(x-a2)2+(y-b2)2=c22，C3:(x-a3)2+(y-b3)2=c23.利用约束方程(19)～(21) 计算保角变换函数称为method 1，利用算法1 计算方程(19)～(21)得到保角变换函数称为method 2.现用method 1 和method 2，分别对该区域到三种狭缝域的保角变换进行数值实验，检验其有效性和精度，保角变换误差由

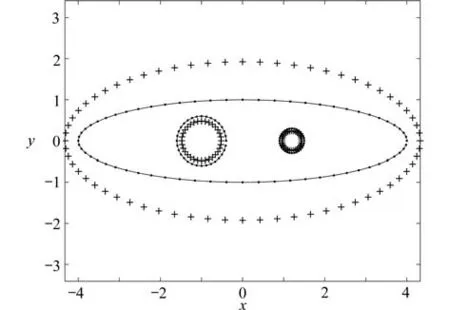
图2 模拟电荷点ζ li和 约束点zkj的分布(N1=64,N2=32,N3=32)Fig.2 The distribution of charge points ζli and collocation points zkj,withN1=64,N2=32,N3=32

确定.表示边界Ck(k=1,2,···,m)上任意两个相邻约束点的中点，且其数量与约束点数量相等.具体操作步骤如下：

步骤1设定模拟电荷点 ζli(l=1,2,···,m;i=1,2,···,Nl)和 对应的约束点zkj(k=1,2,···,m;j=1,2,···,Nk)以及其他参数.

步骤2根据边界条件(11)～(13)确定关于电荷Qil(l=1,2,···,m;i=1,2,···,Nl-1)满足的约束方程.

步骤3求解约束方程，得到电荷Qil(l=1,2,···,m;i=1,2,···,Nl-1)，进而构造近似保角变换函数W(z).

例1a1=4,b1=1;a2=1.2,b2=0,c2=0.3;a3=-1,b3=0,c3=0.6时，根据文献[14]，进行模拟电荷点和约束点的配置.取不同的Nl(l=1,2,3)进行实验，图3为边界曲线映射后的结果.图4是对应的误差曲线，每幅折线图中共有两类六条折线，每一类的三条折线分别表示利用method 1 或method 2，将三条边界映射为狭缝的误差.图中纵坐标是将误差取10为底的对数，横坐标表示电荷点数n.观察可知随着电荷点数n的增加，误差随之减小，当n＞160时，使用method 2的误差曲线，在两条边界上的误差明显优于method 1.

图3 边界保角变换为圆弧狭缝、径向狭缝和平行狭缝(u=0,v=-0.1-0.1i,θ=π/4)Fig.3 Results of boundaries conformally mapped onto circular slits,radial slits and parallel slits,withu=0,v=-0.1-0.1i,θ=π/4

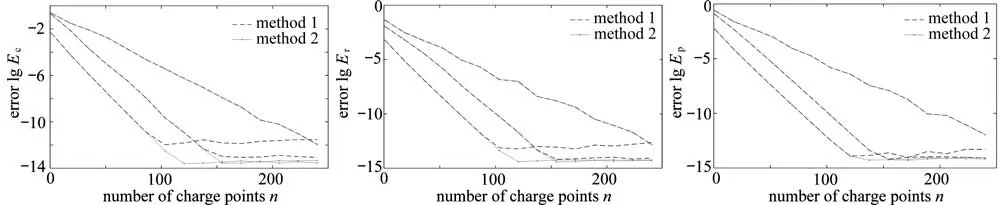
图4 对应图3映射到三种狭缝的数值保角变换误差，此时(N1=N2=N3=n)Fig.4 Numerical conformal mapping errors corresponding to the mappings onto 3 kinds of slits in fig.3,with N1=N2=N3=n

图5给出了将电荷点数调整为N1=2N2=2N3=2n时的误差曲线，观察可知当n＞160时，使用method 2的误差曲线，在三条边界上的误差明显优于method 1.说明本文提出的有界多连通区域数值保角变换的GMRES(m)法可以得到更高精度的模拟电荷Qil(l=1,2,···,m;i=1,2,···,Nl-1).

图5 对应图3映射到三种狭缝的数值保角变换误差(N1=2N2=2N3=2n)Fig.5 Numerical conformal mapping errors corresponding to the mappings onto 3 kinds of slits in fig.3,withN1=2N2=2N3=2n

图6是问题域的边界和内部区域的网格，图7～9为问题域及其网格映射结果的局部放大图.可以看出近似变换函数将有界区域D成功映射为了无界的S(c)，S(r)和S(p,θ).

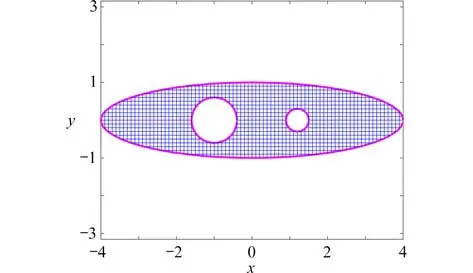
图6 区域D 及其边界Fig.6 Domain D and its boundaries

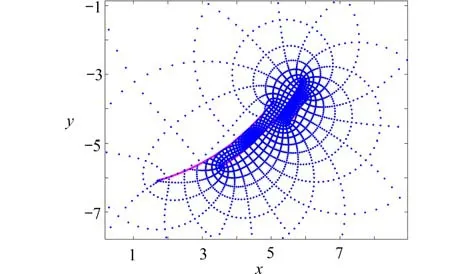
图7 区域D 映射到圆弧狭缝域的像Fig.7 The image of domain D with circular slits

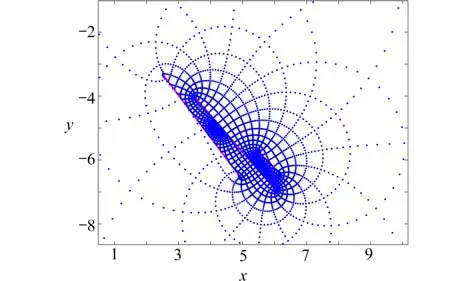
图8 区域D 映射到径向狭缝域的像Fig.8 The image of domain D with radial slits

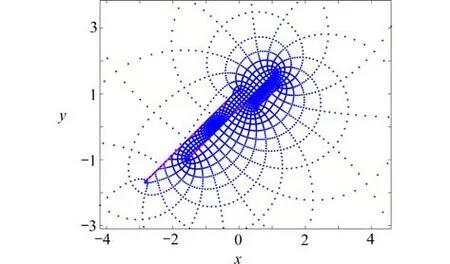
图9 区域D 映射到平行狭缝域的像(θ=π/4)Fig.9 The image of domain D with parallel slits,whereθ=π/4

4 结 论

本文研究了将有界多连通区域映射为三种无界正则狭缝域（圆弧狭缝域、径向狭缝域和平行狭缝域）的数值保角变换.在模拟电荷法的基础上利用GMRES(m)法构造了上述三种狭缝域的高精度的保角变换函数，并通过数值实验验证了本文算法的有效性.今后我们将研究其他形式狭缝域的数值保角变换及其逆变换的算法，并将算法应用到流体力学和图像处理等领域.