含孔曲面自动铺丝轨迹规划算法
2022-10-12冉庆波肖鸿杨富鸿段玉岗
冉庆波,肖鸿,杨富鸿,段玉岗
西安交通大学 机械工程学院,西安 710049
纤维增强树脂基复合材料(Fiber Reinforced Plastics,FRP)由于其高比强度、高比模量、可设计性强和易于整体成型等诸多优点,广泛应用于航空航天、船舶及汽车工业的各种大型构件制造中。为实现特定功能或减少构件重量,通常需在构件表面进行开孔,例如客机机身舱门、窗口及跑车车窗等。因此在自动铺丝轨迹规划阶段实现开孔轨迹规划,从而可在制造阶段完成开孔结构的铺放,节约原材料,降低制造成本,缩短制造周期,具有重要意义。Hyer和Charette采用了一种通过改变纤维丝轨迹方向从而改善开孔构件力学性能的方法,虽然开孔区域应力集中有所缓解,但无法适应复杂含孔曲面。Reuschel和Mattheck以开孔圆桶作为研究对象,通过优化纤维丝轨迹降低最大主应力,充分发挥复合材料力学性能可设计的优点,但同样无法适应复杂曲面。李俊斐等提出投影法进行开孔轨迹边界处理,可以适应较为复杂的含孔曲面,但计算效率较低,无法适应大型复杂构件开孔操作。针对以上通过改变纤维丝轨迹铺放方向达到开孔效果无法适应复杂曲面,以及投影法进行开孔轨迹边界处理计算效率低下无法适应大型构件等情况,本文提出一种基于开孔边界的轨迹规划算法,从开孔边界出发,在保证算法精度的前提下降低计算量,针对开孔边界处理提出基于切线法的延长算法,从效率及精度两个方面对算法进行验证,最后以实际构件铺放实验验证算法的正确性及合理性,算法流程图如图1所示。
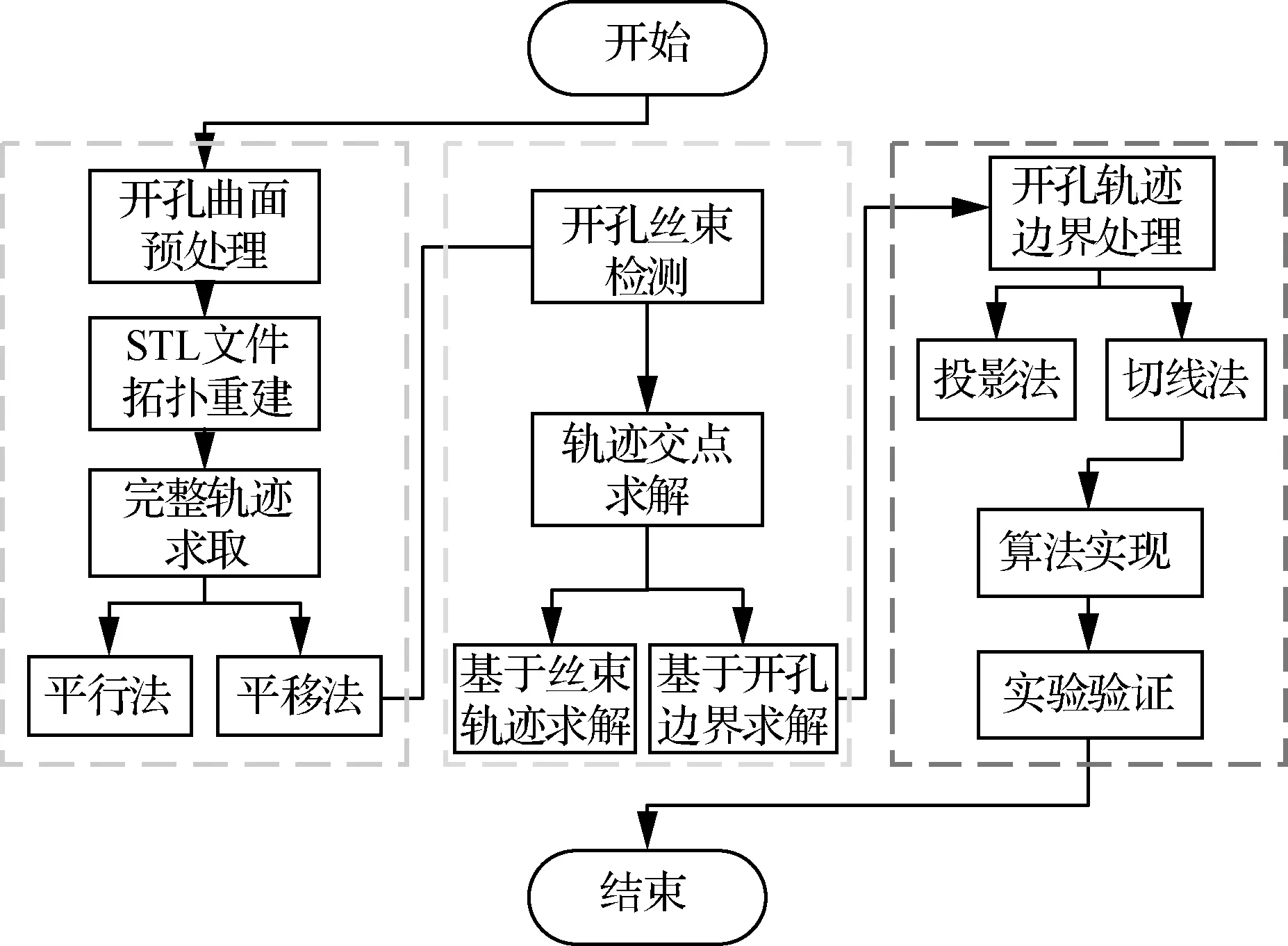
图1 轨迹规划整体算法流程图Fig.1 Overall algorithm flow chart of trajectory planning
1 含孔曲面预处理
1.1 含孔曲面修复
对于轨迹规划,要规划的曲面必须是一个完整的曲面,否则拓扑信息不完整,无法保证生成的轨迹线在开孔两侧一一对应,除此之外其他轨迹线生成也需将之前轨迹线的相关信息用于当前轨迹线的生成及裁剪,如果之前轨迹线几何信息不连续,则会对后续轨迹线的求解造成不便。且自动铺丝过程需制造模具,模具或者模型表面并无开孔,而是一个完整的曲面,所以在制造模具时同样需要完整的曲面信息。因此解决上述问题的方法就是在轨迹规划之前对曲面沿其切线方向进行修复,目的在于既可获取完整的曲面拓扑信息,方便后续的轨迹规划,又可为铺放模具的制造提供必要的数据,如图2 所示。
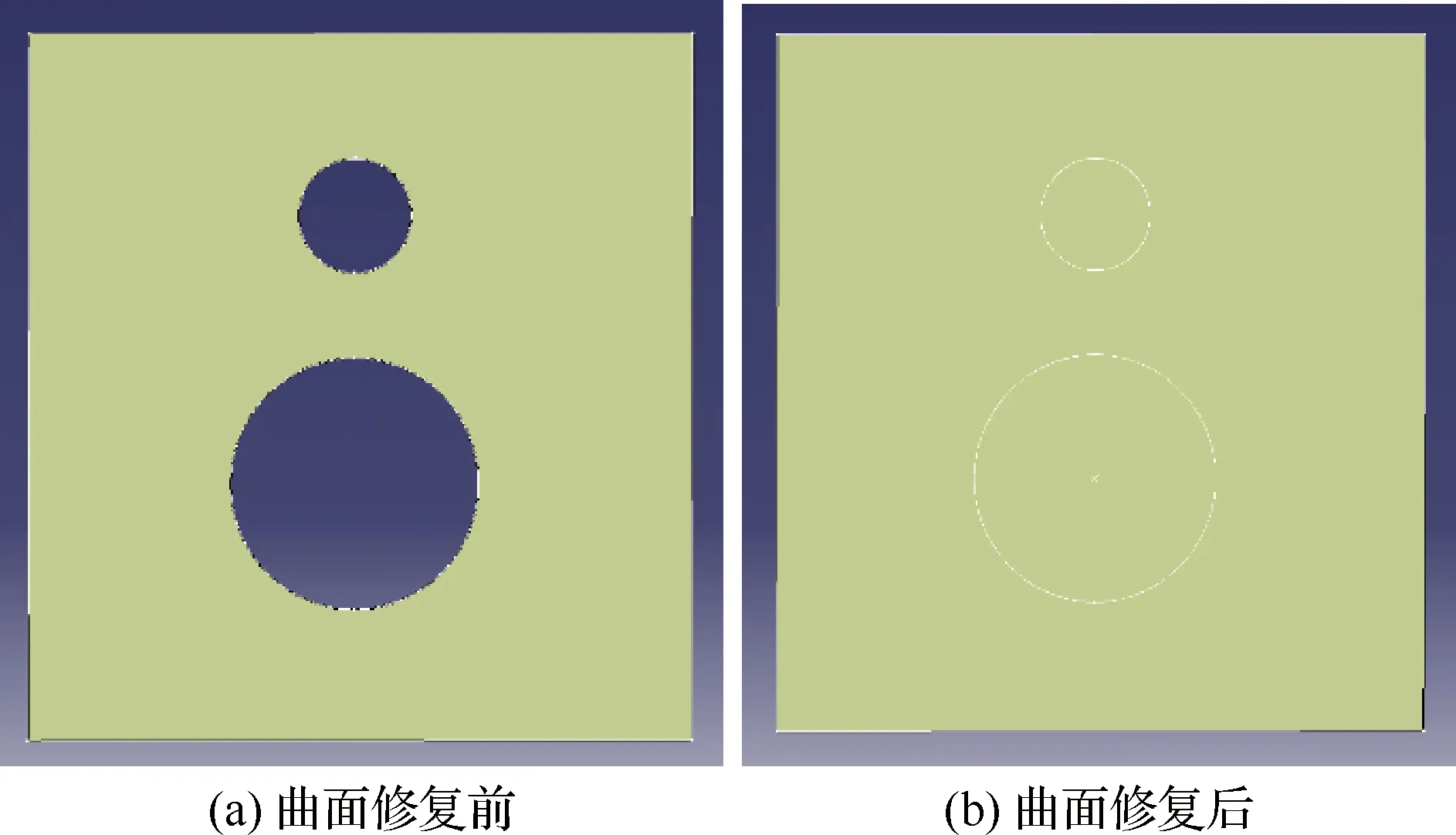
图2 曲面预处理修复前后对比Fig.2 Comparison of surface pretreatment before and after restoration
1.2 含孔曲面STL文件拓扑重建
三角网格信息来自STL文件,其中分别记录了三角形3个顶点的坐标值及其法向量。这种表达方式可将复杂的曲面表示成简单的数学关系,但STL文件信息中并不包含各个三角形之间的拓扑关系,且相邻三角形的同一个点会被重复存储3次、4次甚至更多次,这就造成了在轨迹规划的过程中计算数据量增大,降低了算法的效率,因此将STL文件进行拓扑重建及删除冗余信息势在必行,STL三角网格拓扑关系重建流程如图3所示。
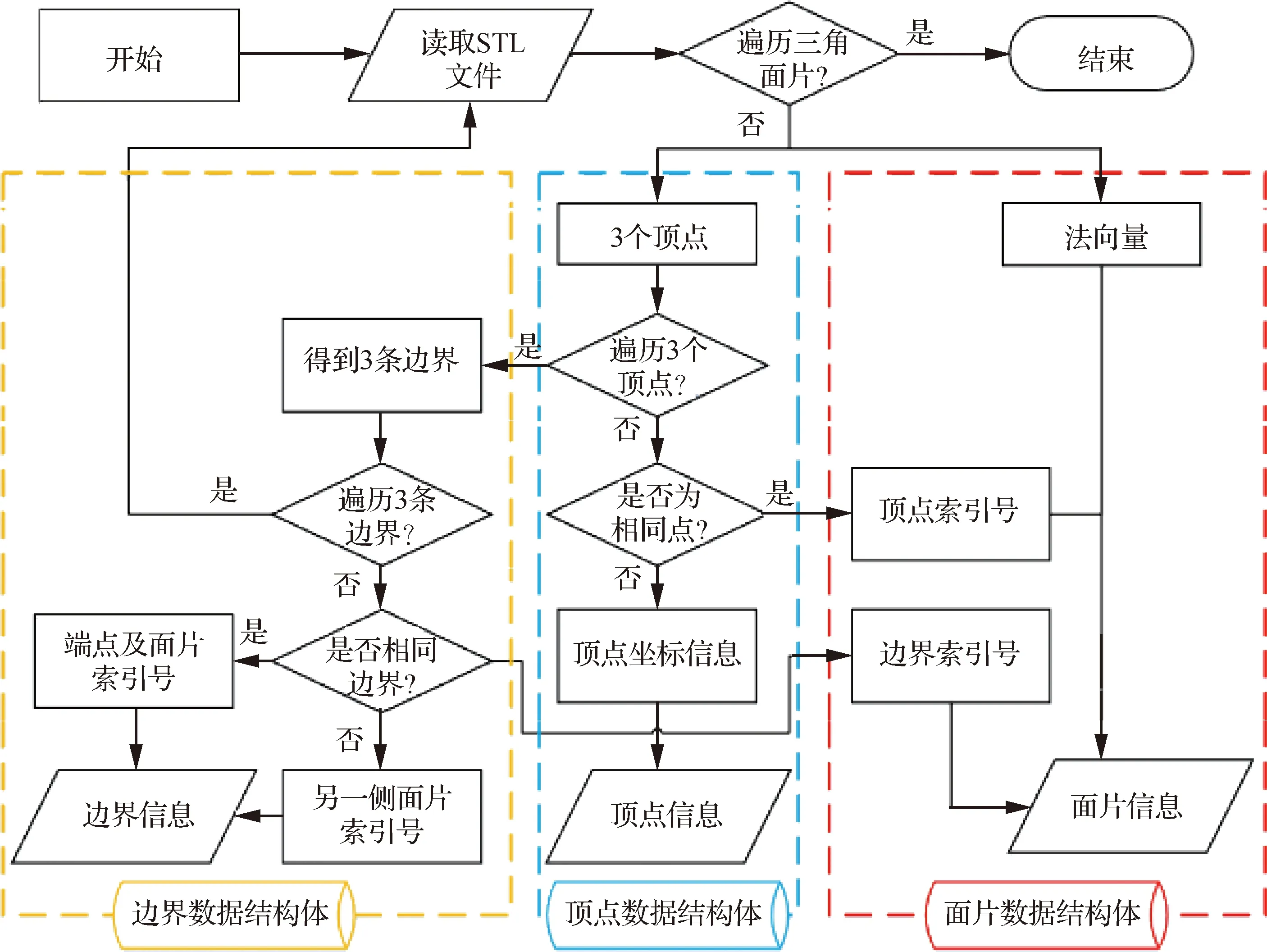
图3 STL文件拓扑重建流程图Fig.3 STL file topology reconstruction flow chart
针对三角面片法轨迹求解的特点,应保证建立后的拓扑关系包括顶点数据结构体、边界数据结构体及面片数据结构体。顶点数据结构体应包含顶点编号、顶点几何坐标值、顶点所在边界及顶点所在三角面片的编号;边界数据结构体应包括边界编号、边界顶点编号及边界所在三角面片编号;面片数据结构体应包括面片编号、面片顶点编号、面片边界编号及面片法向量。STL文件进行拓扑重建的目的在于去除冗余信息降低算法计算量,拓扑重建前后曲面对比如图4所示。
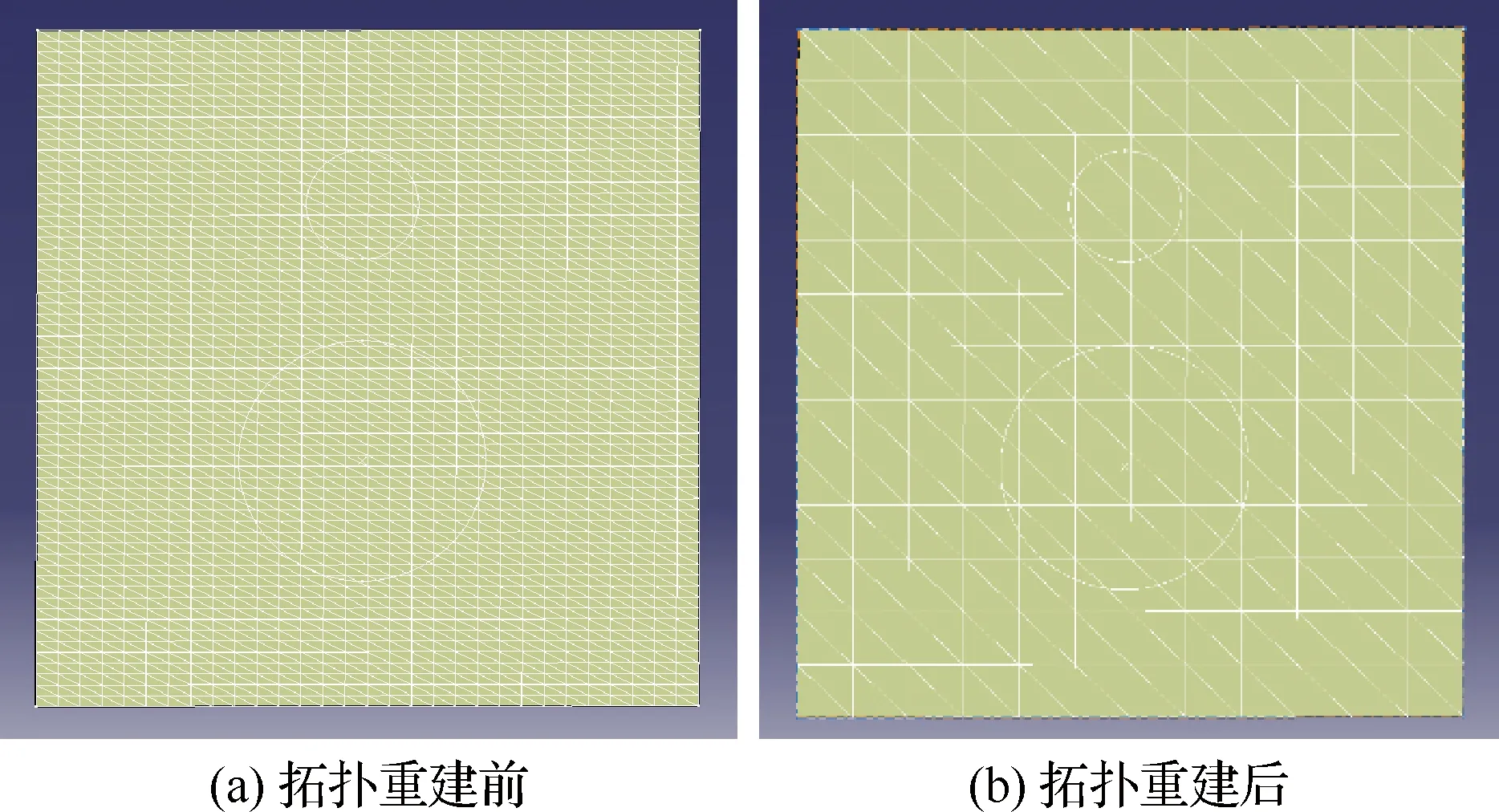
图4 STL文件拓扑重建前后对比Fig.4 Comparison of STL files before and after topology reconstruction
2 含孔曲面轨迹规划
2.1 完整轨迹线求取
初始纤维丝的铺放方向选取一般有两种构造方法:与特定初始参考线成固定角度及与设计的某一方向成固定角度。而基于初始参考轨迹生成后续纤维丝轨迹同样有多种方法,常用的方法有平行法和平移法。平行法虽然可保证纤维丝束之间不产生间隙与重叠,但是不能保证铺放过程中始终沿固定角度铺放,同时也会造成折弯半径曲率过大、纤维丝褶皱等情况,如图5(a)所示。而平移法虽会产生断送纱三角区,但其可保证纤维丝路径始终沿同一角度铺放且不产生褶皱,如图5(b)所示。因此采用平移法进行纤维丝轨迹生成,由于轨迹生成部分并不属于本文重点,在此不再赘述其过程。
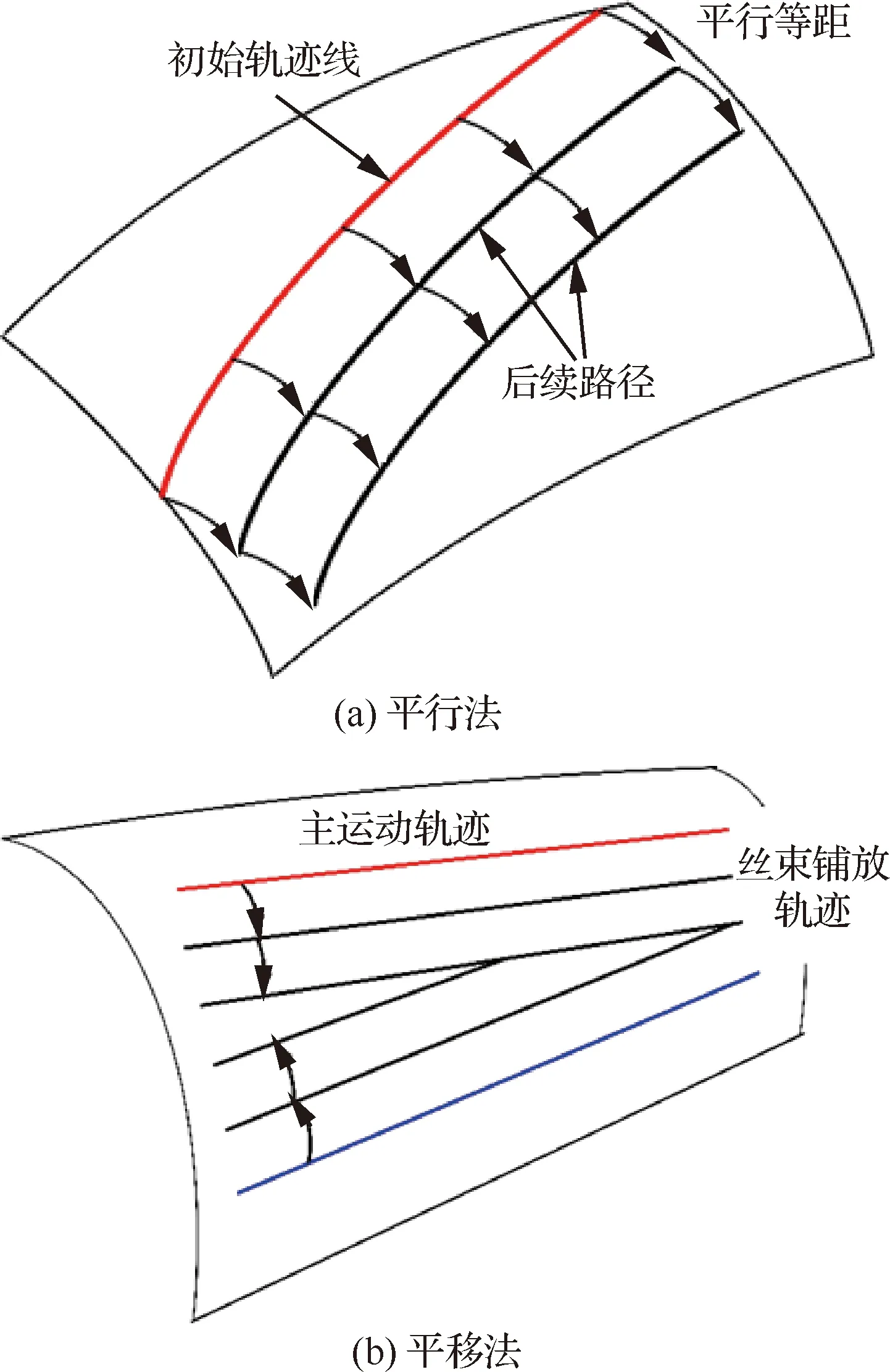
图5 轨迹生成方式Fig.5 Trajectory generation method
2.2 开孔丝束检测
对于一个模型来说需开孔的区域往往只占整体模型面积的很小一部分,因此需进行开孔裁剪的纤维丝轨迹相对于整体轨迹来说也只占很小的一部分。如对所有轨迹全部进行开孔裁剪运算不仅会降低算法效率,同时也会造成算法的稳定性下降,因此提出一种开孔丝束检测方法,以期提高算法计算效率。
首先定义开孔区域近似孔中心点,然后以一定步长遍历开孔边界上所有的点,,…,,计算得到近似孔中心点到开孔边界的最远距离:
=max[(,)]=1,2,…,
(1)
式中:(·,·)为两点之间距离。
如图6所示,以孔中心点为圆心,为半径做圆,则中包含开孔区域。此时根据近似孔中心点到每条纤维丝轨迹投影距离的不同,将纤维丝路径分为3种情况,既没有经过开孔区域也没有经过,没有经过开孔区域但经过,经过开孔区域同时也经过。
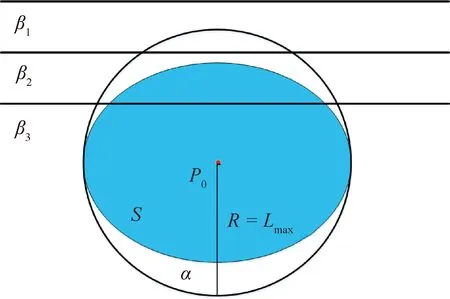
图6 开孔丝束检测示意图Fig.6 Schematic diagram of opening tow detection
此时纤维丝轨迹到距离>不需进行开孔裁剪判断,纤维丝轨迹到距离>需进行开孔裁剪判断但判断后不需进行裁剪,只有纤维丝轨迹到距离>需进行开孔裁剪判断,同时需进行裁剪。针对含孔曲面零件和开孔回转体进气道进行实际测量,需进行裁剪操作的纤维丝轨迹分别减少了89.4%和82.5%,有效提高了算法计算效率。
2.3 开孔轨迹交点求解
根据轨迹点的遍历方式不同,可将求解方式分为基于纤维丝轨迹的交点求解和基于孔边界的交点求解两种方式,对这两种求解方式进行重点讨论。
2.3.1 基于纤维丝轨迹的交点求解
在含孔曲面内,纤维丝边界上的点与孔边界存在着如图7所示3种情况:情况A——点在孔边界外部、情况B——点在孔边界上、情况C——点在孔边界内部。在获取完整的纤维丝轨迹后,可根据孔边界对轨迹进行裁剪处理,具体步骤如算法1所示

算法1 基于纤维丝轨迹的交点求解输入: 纤维丝轨迹β,开孔边界λ输出: 交点所在位置前后两点AB1: for 纤维丝轨迹上第一个点遍历到最后一个点2: if 前后两点全部在边界λ外部(情况A)→不存在交点3: else if 前后两点全部在边界λ内部(情况C)→不存在交点4: else if 存在位于边界λ的点→舍去该点5: else if 一点位于边界λ外部,一点位于边界λ内部→存在交点前后两点6: end

图7 曲面开孔边界处理示意图Fig.7 Schematic diagram of surface opening boundary processing
算例1步骤5是求解交点的关键所在,因此提出利用迭代进行求解的思路。当相邻轨迹点之间出现交点时,首先要连接两点之间的直线,然后再求取纤维丝轨迹与孔边界的交点。已知信息包括两相邻轨迹点的空间坐标信息及三角面片拓扑信息,其中拓扑信息包括两点所在三角面片号、顶点坐标信息及相邻三角面片信息等。基于这些信息可通过迭代的方式反复求解测地线直至找到交点。如图8所示,求解两点之间的交点,具体步骤见算法2。

图8 迭代求解轨迹交点示意图Fig.8 Schematic diagram of intersection of iterative solution trajectory

由于每条纤维丝轨迹长度较长,而大多数轨迹与孔边界只有两个甚至一个交点,却需迭代遍历所有轨迹点才能判断相邻两点之间的位置关系,虽保证了计算精度,但在求解交点的过程中计算量较大,降低了算法的计算效率,且随开孔数量的增加,计算效率将进一步下降。
2.3.2 基于孔边界的交点求解
针对基于纤维丝轨迹的交点求解算法计算效率低下的问题,提出一种基于孔边界的交点求解算法。首先确定交点所在位置,然后精确求解交点位置,算法流程图如图9所示,轨迹交点求解示意图如图10所示,算法具体步骤见算法3。

图9 基于孔边界求解交点算法流程图Fig.9 Flow chart of intersection algorithm based on hole boundary
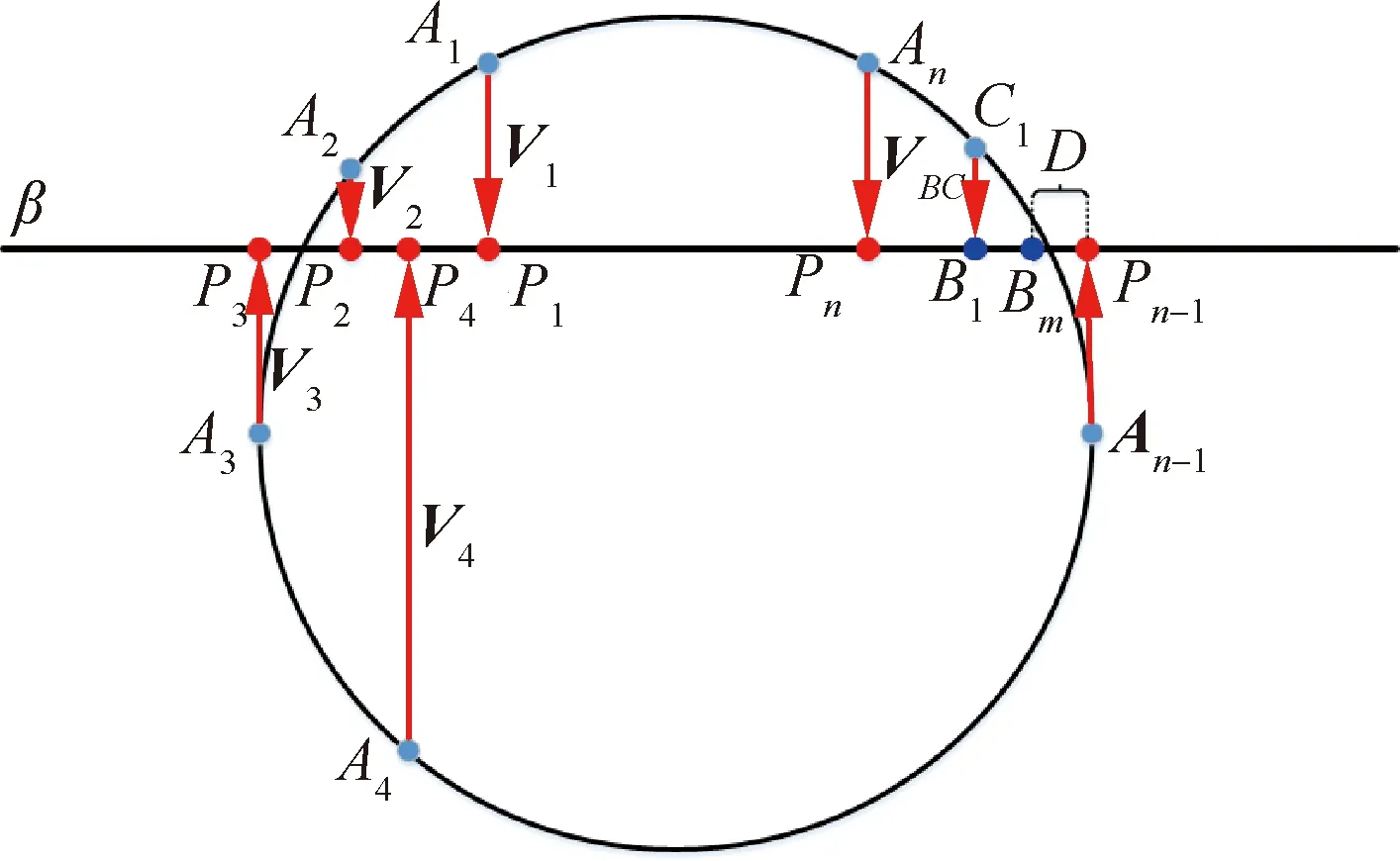
图10 轨迹交点求解示意图Fig.10 Schematic diagram of trajectory intersection point solution


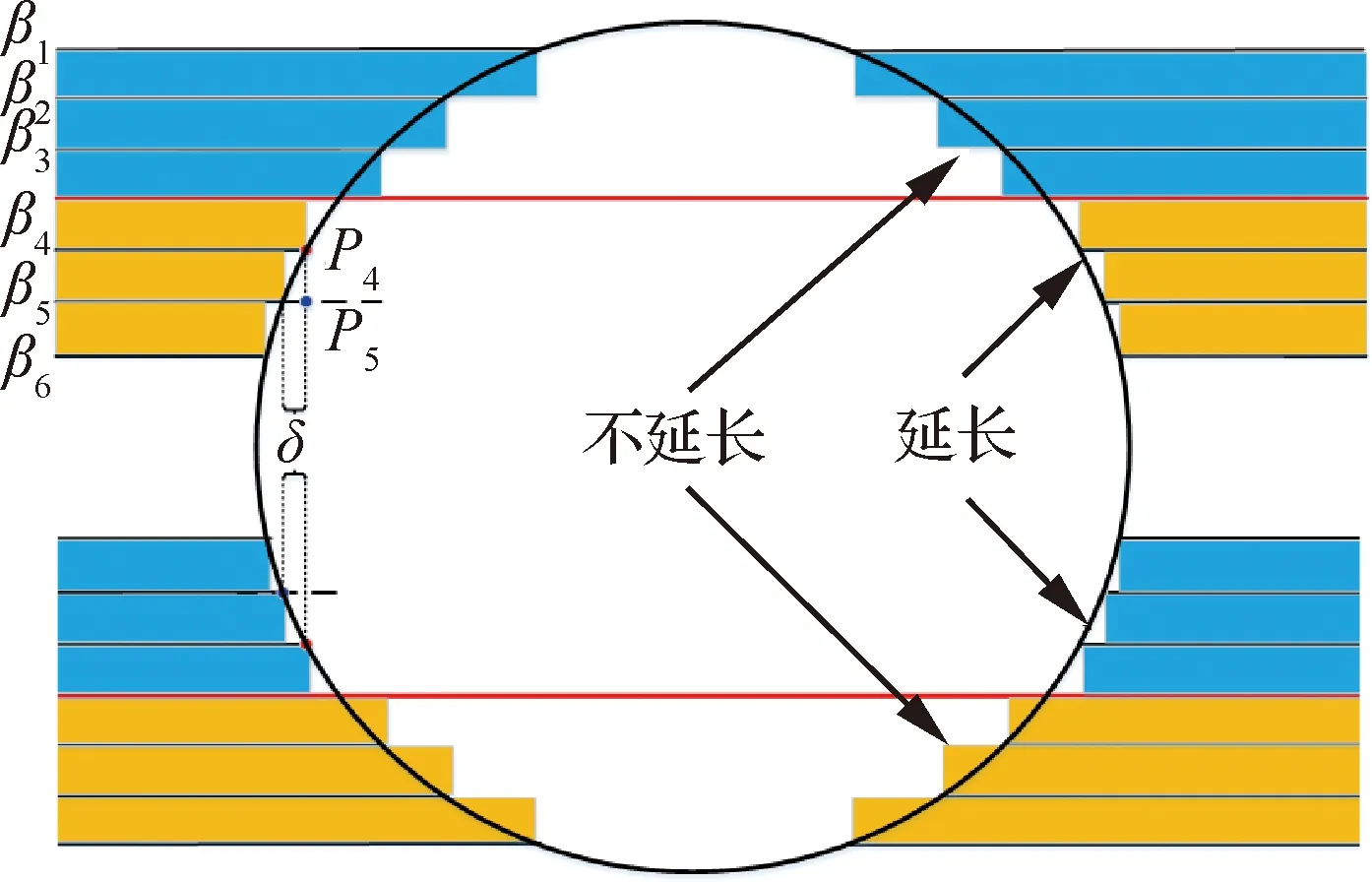
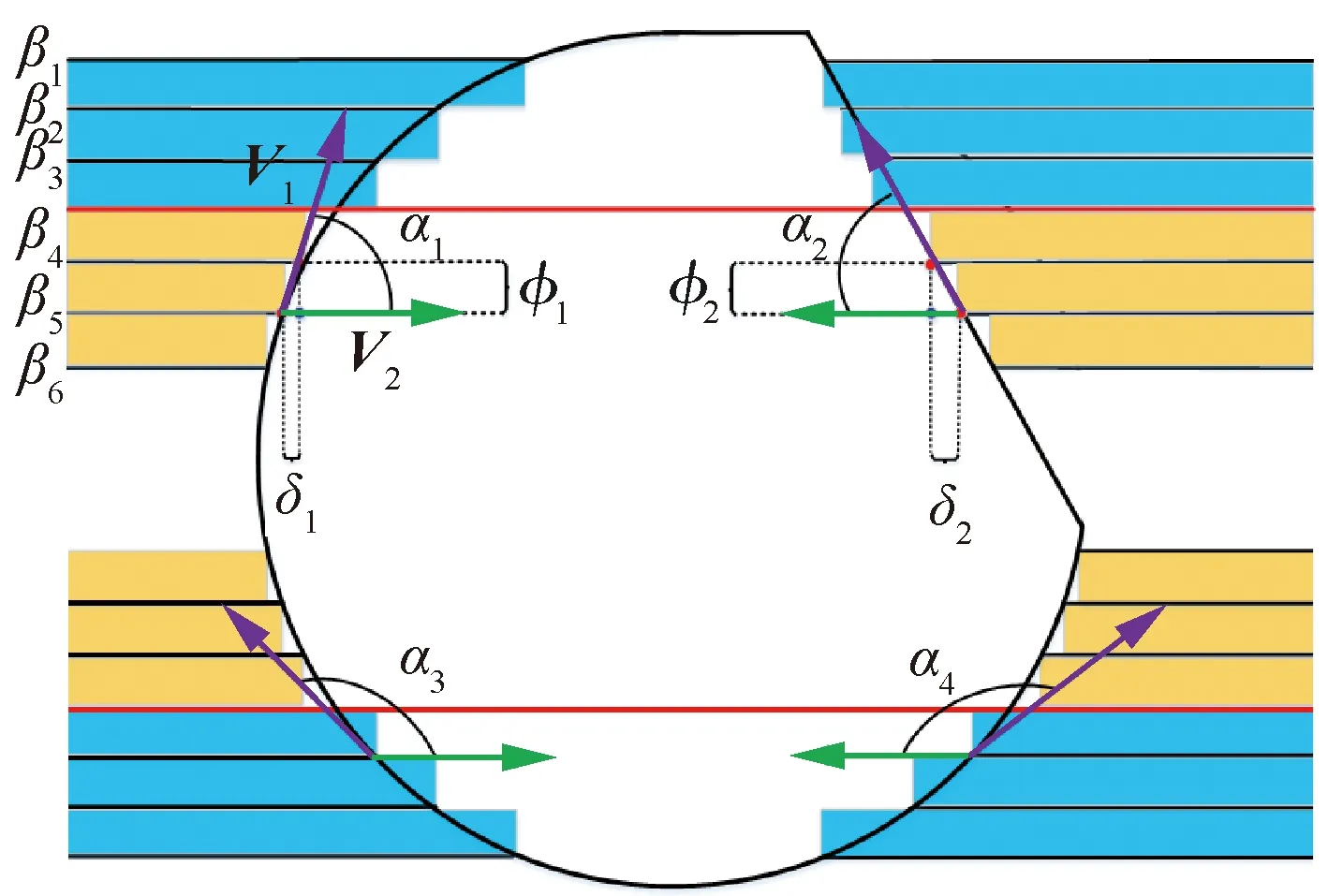
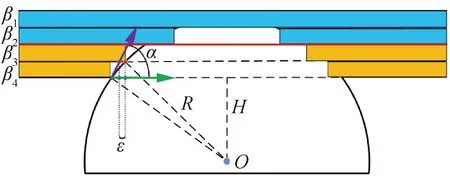
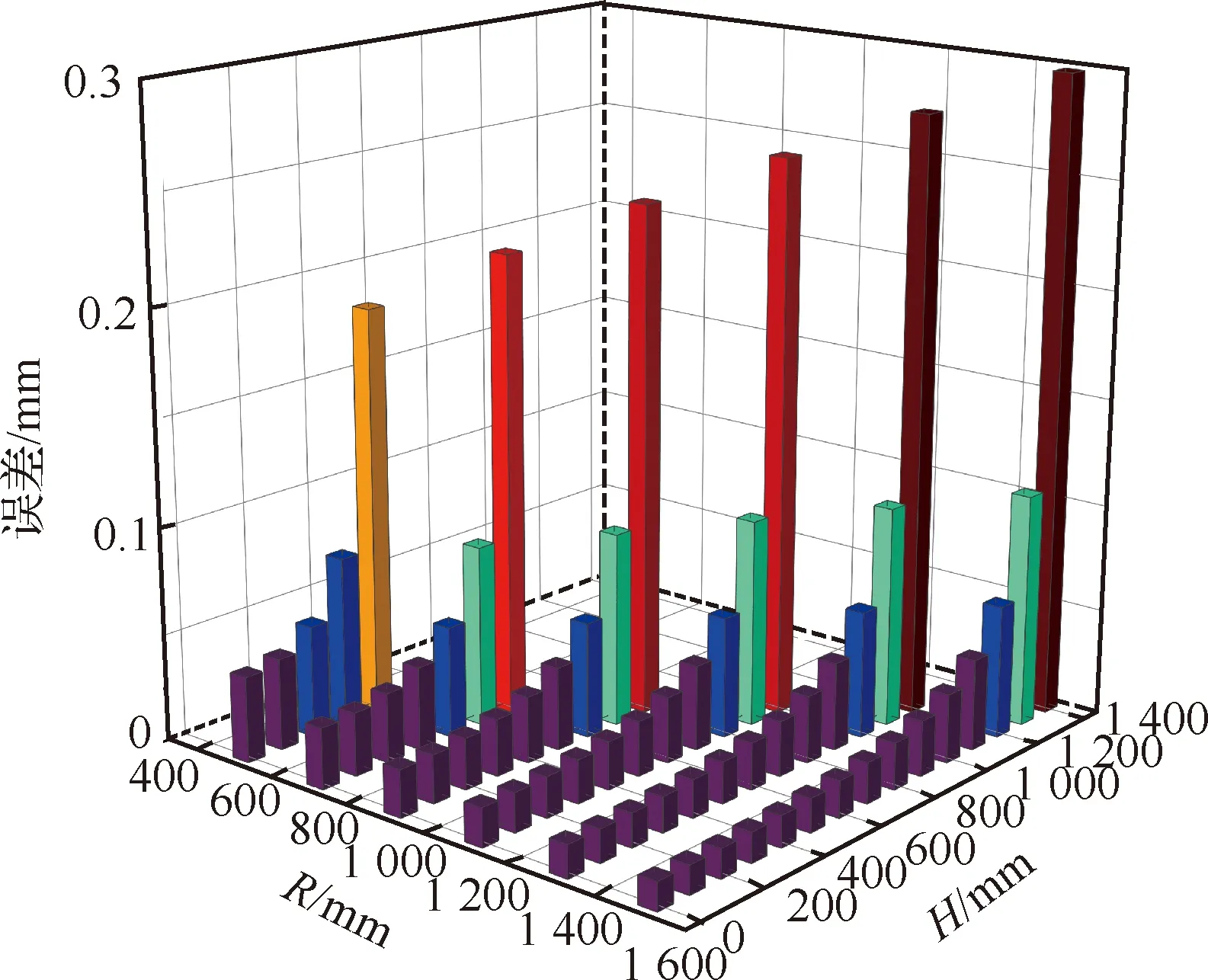
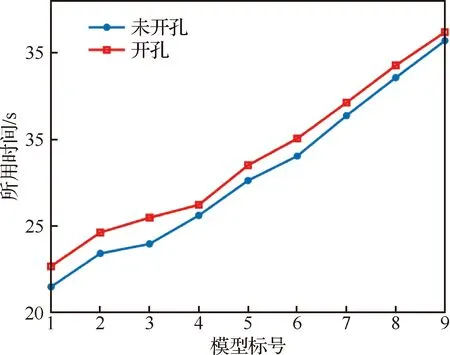
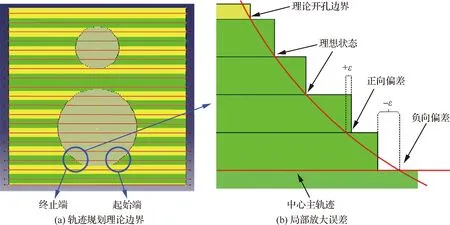
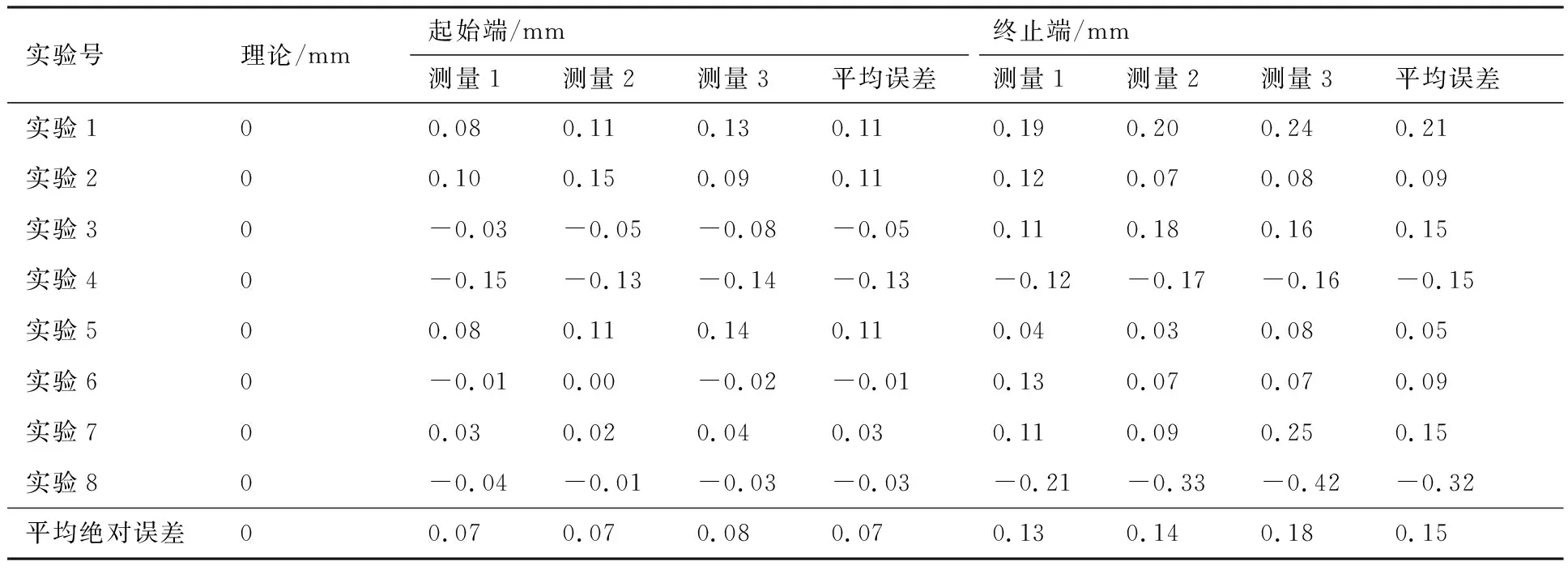
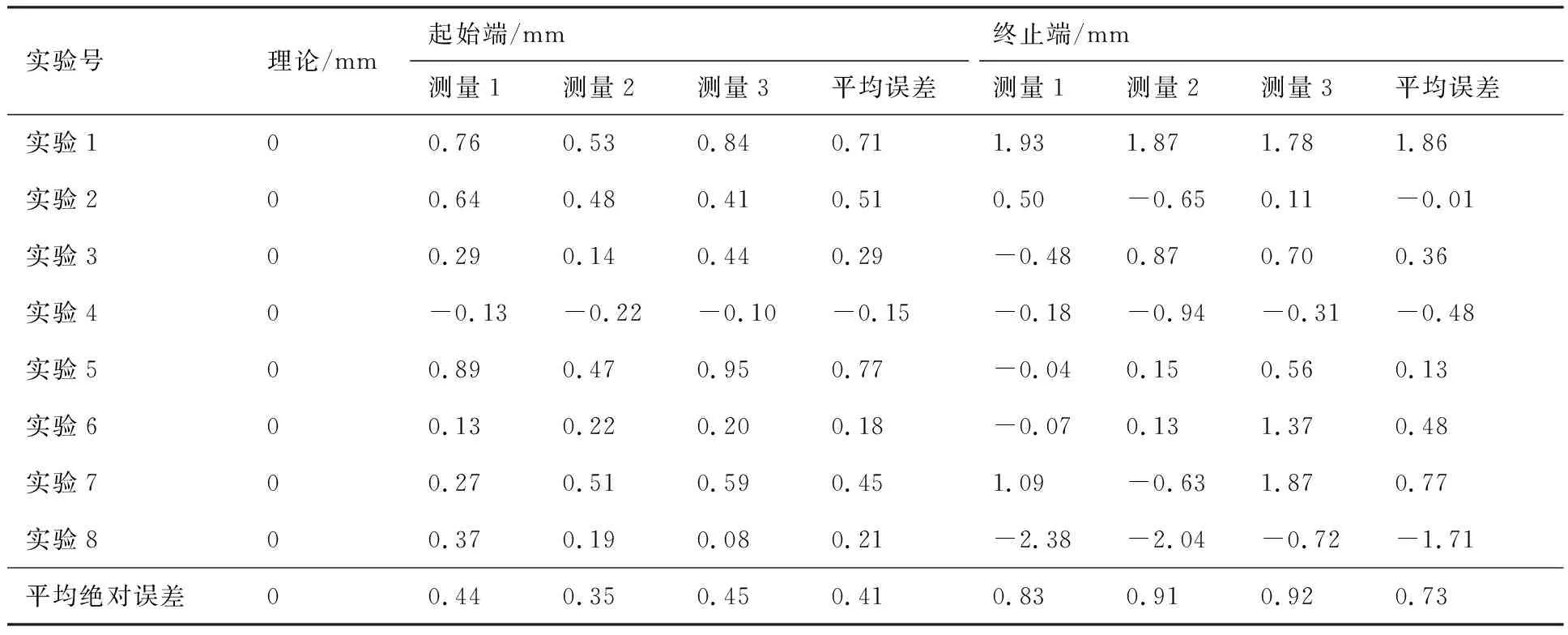
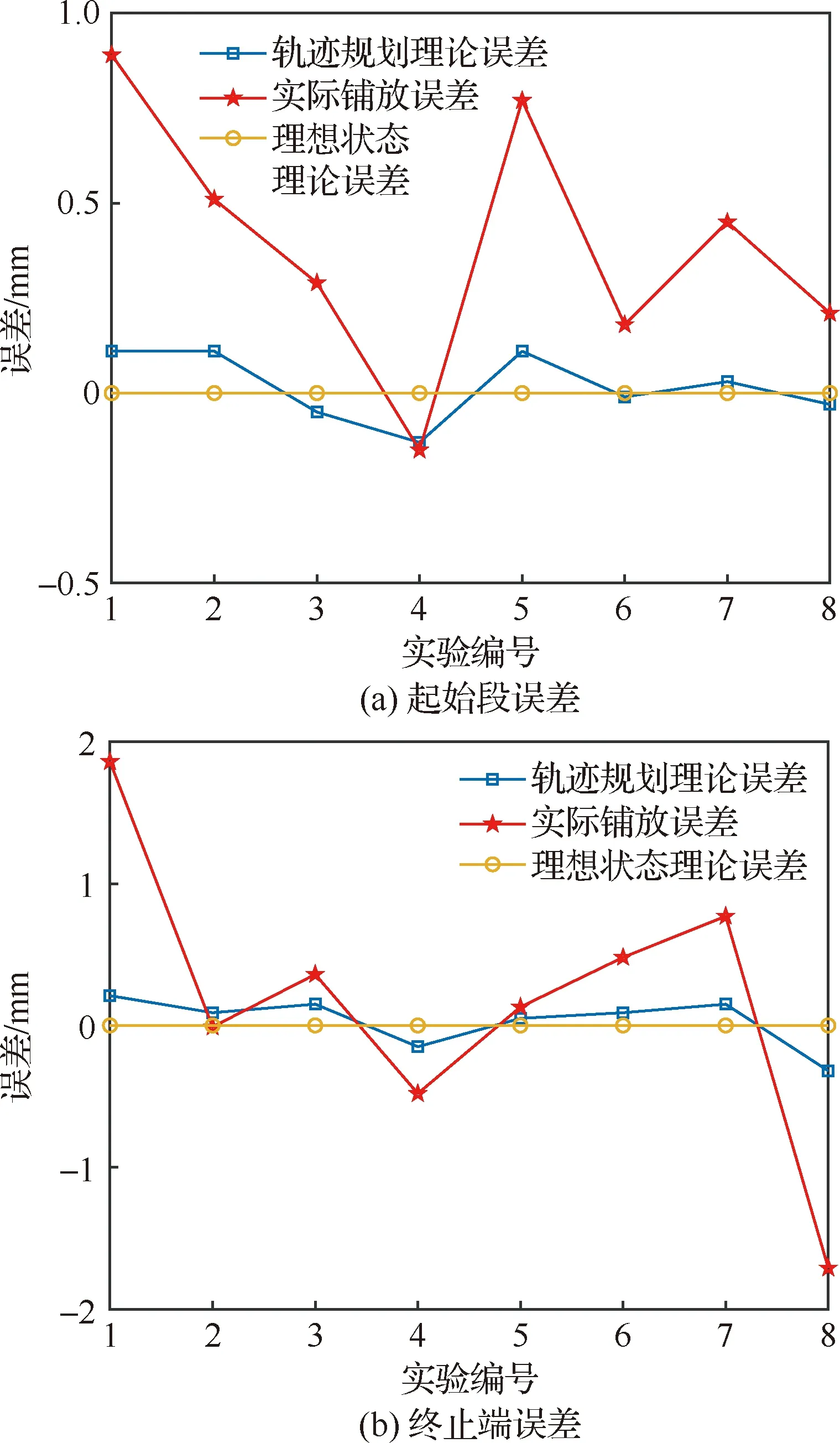
6: for 利用投影点Pn-1、Pn求出其距离二分点B17: 做B1向孔边界最近投影点C1,得到投影向量VBC8: if 向量之间的夹角α>90°→B1处于孔边界内部9: if交点前后两点之间的距离D满足D 由于含孔曲面上纤维丝的轨迹长度远大于孔边界的长度,且每条纤维丝轨迹都要从第一个点开始遍历所有点,尤其当曲面尺寸变大时计算量更是成倍增长。与基于纤维丝轨迹的求解方法相比,基于开孔边界的求解方法无需进行大量轨迹点的迭代操作,只需求解投影向量改变方向的两点即可。除此之外,为保证交点求解精度,通过多次求解距离二分点可将误差以指数级迅速降低,从而满足开孔裁剪精度。因此基于孔边界的交点求解方法虽精度上比基于纤维丝轨迹的交点求解方法有所欠缺,但其计算效率远高于基于纤维丝轨迹的交点求解方法。当求解二分点次数足够多时算法精度可得到保障,即采用基于孔边界的交点求解方法在保证求解精度的同时也保证了求解过程中的计算效率。 由于纤维丝束具有宽度,而轨迹规划一般只需规划纤维丝束外侧边界,因此并不能简单地以轨迹与孔边界的交点作为断点,如图11所示。 图11中红色轨迹代表铺丝设备运动主轨迹,不进行裁剪。对于上半圆,主轨迹上侧纤维丝轨迹如果以交点为断点,则可完全覆盖含孔曲面,主轨迹下侧纤维丝轨迹如果交点为轨迹断点,则会形成空白三角区。但对于下半圆则相反,主轨迹下侧纤维丝轨迹以交点为断点,则可完全覆盖含孔曲面,主轨迹上侧纤维丝轨迹以交点为轨迹断点,则会形成空白三角区。三角区的存在会造成构件开孔区域力学性能下降,因此纤维丝轨迹需延长,确保其能完整覆盖曲面。针对轨迹边界延长提出投影法和切线法两种延长算法。 图11 轨迹规划边界三角区Fig.11 Triangle area of trajectory planning boundary 2.4.1 投影法 由图11可发现对于上半圆,空白区域的长度是上一条纤维丝轨迹与孔边界的交点和当前纤维丝轨迹与孔边界交点在纤维丝轨迹方向的长度,对于下半圆,结论同样适用,只不过此时变成主轨迹上侧纤维丝轨迹需延长。因此提出一种投影法计算延长距离,具体步骤见算法4。 算法4 投影法求解延长点输入: 两条纤维丝轨迹β4、β5输出: 是否需要延长及延长距离δ1: β4与孔边界的交点P4向β5进行投影,得到投影点P52: if投影点P5属于孔边界内部(通过2.3.2节中的算法进行判断)3: →不需要延长4: else →需要延长,且延长距离δ5: end 虽投影法精度可得到保证,但多次投影求解也会降低算法计算效率。 2.4.2 切线法 针对投影法投影运算降低计算效率的问题提出切线法,避免投影法的缺陷。如图12所示,主要是求解延长距离,具体步骤见算法5。 对于圆的上半部分,如图12所示,左上侧主轨迹下侧纤维丝轨迹向量之间的夹角、小于90°,需要延长,上侧不需要延长。而对于圆的下半部分,如图12所示,下半圆的主轨迹下侧纤维丝轨迹向量夹角大于90°,不需延长,因此切线法对于整圆全部都是适用的。对于开孔边界是直线的情况,如图12右上侧直线开孔边界所示,由于纤维丝轨迹与孔边界的交点做出孔边界的切线向量与孔边界方向一致,因此无论是投影法还是切线法求得的延长距离相同,不存在误差。而对于开孔边界是曲线的情况,如图12左上侧曲线开孔边界所示,由于纤维丝轨迹与孔边界的交点做出孔边界的切线向量与孔边界方向并不一致,因此投影法与切线法求得的延长距离并不相同,存在误差。由于开孔边界曲线并没有一般规律,因此误差也没有特定计算公式,但是在很小的范围内(纤维丝束宽度一般为6.35 mm)可近似认为开孔边界曲线是一段圆弧,因此可得出误差计算公式。 图12 切线法求解延长距离Fig.12 Tangent method for solving extended distance 如图13所示,为开孔区域圆心,则切线向量与纤维丝轨迹方向向量之间的偏转角的计算公式为 (5) 切线法延长距离计算公式为 (6) 投影法延长距离计算公式为 (7) 因此可计算出切线法与投影法之间的误差为 (8) 图13 切线法求解延长距离误差计算Fig.13 Calculation of error of extended distance by tangent method 从式(8)中可分析出误差的大小只与开孔区域半径和纤维丝束所在高度有关。 从图14中可发现,在高度一定的情况下,随开孔半径的不断增大,误差不断减小;在开孔半径一定的情况下,随高度增大,误差也随之增大,但两者的误差都在纤维丝自动铺放允许的精度之内,因此算法可保证开孔边界精度。 图14 切线法求解延长距离相对误差Fig.14 Tangent method for solving relative error of extended distance 纤维丝自动铺放过程涉及多方面内容,信息复杂,计算量大,且需保证获得的铺放信息准确无误,搭建自动铺丝CAD/CAM软件系统是实现复合材料自动化快速成型的重要保证。在第2节设计算法的基础上搭建软件开发平台,为提高算法的通用性及兼容性,选取在航空航天领域通用的CAD/CAM平台CATIA作为软件开发平台,基于Visual Studio 2005软件,采用CATIA V5 Component Application Architecture (CATIA V5 CAA)技术实现算法。 为检验所提轨迹规划算法,特别是铺放路径在开孔处的轨迹规划情况,分别以开孔平板及开孔回转体进行算法验证。以丝束数量为8、丝束宽度为6.35 mm进行轨迹规划,开孔平板及开孔回转体轨迹规划效果如图15所示。 图15 开孔构件轨迹规划效果Fig.15 Trajectory planning effect of perforated components 为进一步验证开孔轨迹规划效果及精度,利用课题组自主研发的8丝束铺丝头,集成重送、剪切、夹持、加热、压紧等模块,对开孔平板、开孔回转体进行实际铺放,铺放材料为美国赫氏公司HexPlyM21碳纤维,标称带宽为(6.350±0.125) mm,铺放实验时室温为23 ℃,加热温度为35 ℃,铺放速度为150 mm/s,铺放压力为500 N。 开孔构件实际铺放效果如图16所示。从轨迹规划及实际铺放效果看,各丝束均能准确到达边界且自动判断是否延长及延长距离,因此提出的基于开孔边界的轨迹规划算法能高效地对开孔构件进行轨迹规划,且符合实际工程需求。 开孔轨迹规划算法的规划效率指的是该算法铺放完成一个具体模型所需的时间,为验证提出的开孔规划算法的效率,按曲面复杂程度及曲面铺放面积由小到大选取了9个模型,分别计算其开孔与未开孔情况下规划完成整个曲面所需的时间,结果如图17所示。 从图17中可看出随模型复杂程度增加及铺放面积增大,规划轨迹所需时间也随之增加,另外开孔与否对整个曲面轨迹规划所需时间影响并不大,平均时间增加3.41%,并没有明显降低整体算法效率,且随模型复杂程度增加及铺放面积增大,开孔与未开孔轨迹规划之间的时间差越来越小,这是由于丝束程度对基于开孔边界的轨迹规划算法并没有影响,随曲面增大,开孔所需时间占总体规划时间越来越少,进一步证明了所提基于开孔边界的轨迹规划算法的优越性。 图17 轨迹规划效率对比Fig.17 Comparison of trajectory planning efficiency 轨迹的边界精度是指铺放成型丝束的边界与设定边界的差异,其中纤维丝束边界包含起始边界和结束边界,在轨迹中分别通过重送指令和剪切指令进行控制。边界误差是一个综合误差,包含丝束重送长度和剪切长度的测量误差、机器人的定位误差、在轨迹规划阶段算法设置的边界覆盖策略误差及边界裁剪精度。为验证提出的开孔边界裁剪算法的准确性,将以平板标准测定模具的0°轨迹100%覆盖为例进行规划测试,验证算法边界精度。 3.3.1 轨迹规划理论边界精度验证 对轨迹规划理论边界精度进行测量,验证轨迹规划边界精度。轨迹规划丝束效果及边界精度误差如图18所示。标称带宽6.35 mm作为轨迹规划标准带宽,0°轨迹100%覆盖策略的测量实验数据如表1所示。 图18 轨迹规划理论边界误差示意图Fig.18 Schematic diagram of theoretical boundary error of trajectory planning 表1 100%覆盖策略轨迹规划理论边界误差 对于实际的轨迹规划,过高的精度对最后的铺放效果并没有实际意义,只会引起计算机求解迭代次数过多,造成计算机资源浪费。通过表1轨迹规划边界延长精度实验数据可看出,对于提出的开孔轨迹规划算法,轨迹规划纤维丝束的理论边界控制精度平均绝对误差为0.11 mm,满足航空航天铺丝工艺边界精度要求。 3.3.2 实际铺放边界精度验证 为测量实际边界精度,验证边界控制精度,对100%覆盖策略的0°轨迹进行实际铺放,铺放丝束效果及边界测量示意图如图19所示。同时实验前在平板模具上先行测量设备的重送距离和剪切距离,经实验铺放测量量设定重送距离为97 mm,剪切距离为98 mm。 图19 实际铺放边界及局部放大测量Fig.19 Actual laying boundary and local enlarged survey 取美国赫氏公司HexPlyM21碳纤维的标称带宽为6.35 mm,100%覆盖策略的测量实验数据如表2所示,可知对于提出的开孔轨迹规划算法,纤维丝束的实际铺放边界控制精度平均绝对误差为0.57 mm,满足航天航空铺丝工艺边界精度要求。 表2 100%覆盖策略实际铺放误差 3.3.3 误差分析 为更加清晰地分析提出的开孔轨迹规划算法误差来源,将起始端和终止端3种误差统一分析。 从图20中可看出理想状态的轨迹规划理论误差一直是0,而轨迹规划理论误差由于计算机资源及算法计算效率的限制,不可能无限制地逼近理论误差,因此只需满足误差在一定可接受的范围内即可。对实际铺放来说,由于实际铺放误差是一个综合误差,不仅包含在轨迹规划阶段算法设置的边界覆盖策略误差、边界裁剪精度,还包含丝束重送长度和剪切长度的测量误差、机器人的定位误差。因此实际铺放误差大于轨迹规划理论误差,但与轨迹规划理论误差变化趋势相同。 图20 轨迹误差分析Fig.20 Trajectory error analysis 针对大型复杂开孔构件轨迹规划,主要对以下内容进行了研究: 1) 研究了纤维丝轨迹生成方式,提出修复含孔曲面不仅可获取完整的曲面拓扑信息,方便后续的轨迹规划,又可为铺放模具的制造提供必要数据。对修复完成的曲面通过STL文件提出三角网格信息,并重建网格之间的拓扑信息。通过纤维丝轨迹与近似孔中心点的几何关系确定需要裁剪的纤维丝轨迹,降低算法计算量。 2) 针对开孔边界交点问题提出基于纤维丝轨迹的交点求解及基于孔边界的交点求解两种算法,通过对两种算法的优劣势对比,最终决定采用基于孔边界的交点求解算法,此算法在满足精度要求的前提下可大幅度提升算法效率。 3) 针对纤维丝轨迹孔边界处理问题提出投影法和切线法两种延长算法,通过研究发现两种算法都可满足边界裁剪精度要求,但相比于投影法,切线法计算量更小,算法效率更高,因此采用切线法进行开孔边界处理。 4) 对CATIA软件进行二次开发,基于Visual Studio 2005软件平台采用CATIA V5 CAA技术实现算法,并针对不同构件进行算法验证,对开孔平板及开孔回转体进行实际铺放实验,证明了算法的正确性且验证了其符合实际工程需求。对不同曲面复杂程度及曲面铺放面积的9个模型进行轨迹规划,结果显示开孔与否对整个曲面轨迹规划所需时间影响并不大,平均时间增加3.41%,开孔并没有明显降低整体算法效率。通过对平板标准测定模具的0°轨迹100%覆盖算例进行规划测试,验证了轨迹规划边界精度平均绝对误差为0.11 mm,实际铺放边界精度平均绝对误差为0.57 mm,最终对误差进行分析,满足航天航空铺丝工艺边界精度要求。2.4 开孔轨迹边界处理


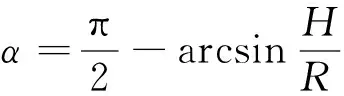
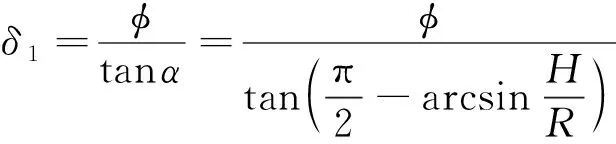
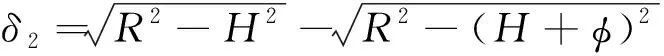

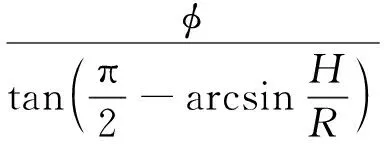
3 算法实现与实验验证
3.1 开孔轨迹规划算法铺放验证


3.2 开孔轨迹规划算法效率验证
3.3 开孔轨迹规划算法精度验证

4 结 论
