旋转裂纹叶片-弹性轮盘耦合系统振动特性

2022-10-12吴志渊闫寒吴林潮马辉瞿叶高张文明

航空学报 2022年9期

吴志渊,闫寒,吴林潮,马辉,瞿叶高,张文明,*

1. 上海交通大学机械系统与振动国家重点实验室,上海 200240 2. 东北大学机械工程与自动化学院,沈阳 110819

随着航空发动机研制技术的发展和服役性能要求的提高,以及在高速、高温、重载和强扰动等极端服役环境下的运行工作,与航空发动机叶片相关的裂纹、碰摩和脱落等失效问题越来越突出,也越来越受到国内外学者的关注。由于航空发动机叶片长期受到交变的机械载荷激励、气动载荷激励以及温度载荷激励,极易导致叶片发生振动进而引发高周疲劳；以及对高速运转设备进行频繁启动-停机操作导致叶片引发低周疲劳；甚至由于发动机在运行环境中吸入各种颗粒物对叶片造成损伤,降低了叶片抗疲劳的能力加速叶片的损伤断裂。因此,研究叶片裂纹对系统的影响对航空发动机健康检测具有重要意义。

真实叶片形状复杂,因此,许多学者基于集中质量模型、梁模型、板壳模型和三维实体模型对叶片进行了简化处理,研究了其复杂的振动问题。考虑梁模型在叶片建模中具有较高的精度和效率,因此梁模型被学者们广泛应用。Behzad等基于线弹性断裂力学理论将每个裂纹等效为无质量旋转弹簧,研究了裂纹梁固有频率、裂纹位置和等效弹簧刚度之间的关系。Dado和Abuzeid考虑裂纹梁弯曲和轴向之间的模态耦合,采用裂纹柔度矩阵耦合的两段连续梁方式建立了自由端带有质量和转动惯量的裂纹悬臂梁动力学模型。由于含有裂纹的叶片刚度会随着载荷的变化不断改变,并且裂纹不可能在叶片振动过程中一直保持常开状态,因此许多学者针对裂纹“呼吸效应”做了大量研究。Xie等考虑到离心效应、呼吸效应和裂纹效应的耦合,提出了一种带有呼吸裂纹的旋转叶片振动建模方法,并构造了由离心应力引起的附加弯矩。Zhao等基于应变能释放率和Castigliano原理建立了裂纹梁单元模型,并根据裂纹面在振动过程中的闭合区域考虑了裂纹的呼吸效应建立了扭形旋转裂纹叶片的有限元模型。Yang等引入弯曲应力与离心应力之间的耦合效应,对基于振动的双线性呼吸裂纹模型和余弦呼吸裂纹模型进行了修正。

随着研究的进一步深入,许多学者考虑轮盘对裂纹叶片的影响并进行了研究。Huang和Kuang采用Galerkin方法,建立基于Euler-Bernoulli梁模型的裂纹叶片-刚性轮盘系统模型,通过应力强度因子积分得到的附加应变能计算裂纹导致的附加柔度。Kuang和Huang研究中采用了多叶片的连续参数模型,用裂纹来模拟叶片的失谐,同时在建模时考虑到叶片的预扭角,分析裂纹失谐对叶片振动特性的影响。Fang等建立了航空发动机叶片-轮盘简化模型,重点研究了叶片间的耦合作用、裂纹的大小、激励模式和叶片数量等对裂纹叶片的振动响应影响。

由上述文献可知,现有理论模型大多基于含裂纹的单叶片,针对裂纹叶片-轮盘耦合系统的研究大多基于刚性轮盘假设,因此,建立裂纹叶片-弹性轮盘的理论模型具有重要意义,且连续体动力学模型具有较好的物理解释性和较高的计算效率,便于揭示裂纹机理。基于Kirchhoff理论模拟弹性轮盘以及Timoshenko理论模拟叶片,基于释放应变能和Castigliano原理将叶片裂纹等效为旋转刚度,建立了裂纹叶片-弹性轮盘耦合系统连续体动力学模型；并通过实验和有限元方法验证了模型的有效性和准确性；最后,详细分析了裂纹深度、裂纹位置、轮盘厚度和旋转速度对裂纹叶片-弹性轮盘耦合系统固有特性的影响规律,为叶片-弹性轮盘系统的裂纹诊断提供了一定的理论依据。

1 动力学建模

旋转叶片-弹性轮盘耦合系统的模型示意图如图1所示,假设弹性轮盘内径固支约束,叶片均匀分布在弹性轮盘上,且与弹性轮盘刚性连接,考虑弹性轮盘的横向位移以及叶片的径向位移、横向位移和剪切角,基于Kirchhoff板理论对弹性轮盘进行建模,基于Timoshenko梁理论对旋转叶片进行建模。

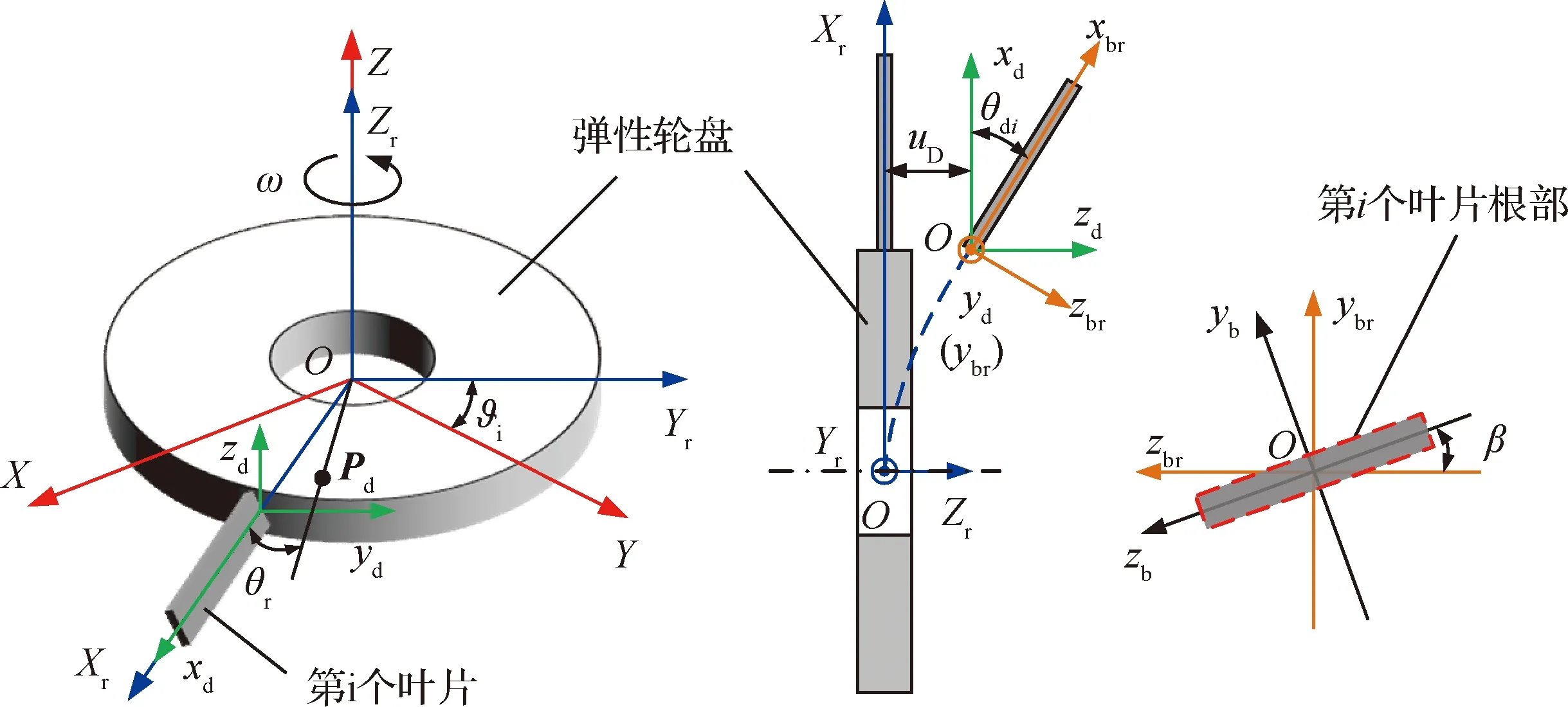
图1 旋转叶片-弹性轮盘耦合系统模型示意图Fig.1 Model schematic of rotating-blade-flexible-disk coupling system

1.1 弹性轮盘建模

轮盘在固定坐标系下的动能为

(1)

式中：、、和分别为轮盘内径、外径、厚度和密度；、分别为轮盘任意点在极坐标下的坐标；为轮盘任意点的横向位移；为轮盘旋转角速度；为轮盘极转动惯量。

考虑轮盘旋转导致的离心刚化,轮盘的弹性势能为

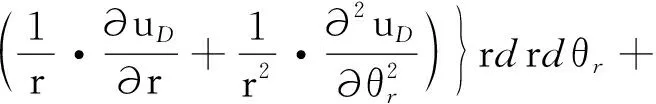
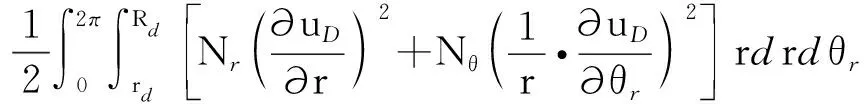
(2)

(3)

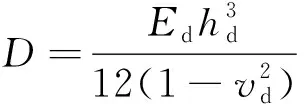
(4)

(5)

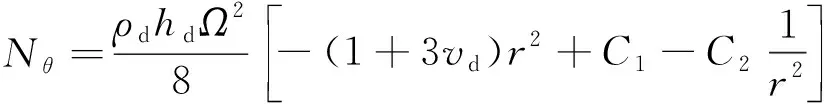
(6)

(7)

(8)

式中：为轮盘的弹性模量。

1.2 健康叶片建模

考虑叶片径向、横向位移和剪切角,第个叶片上任意点在固定坐标系下的位置为

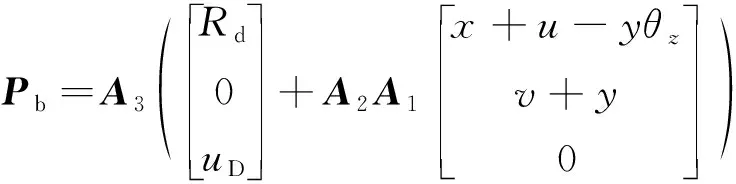
(9)

式中：和分别为叶片局部坐标系中沿着叶片长度方向和厚度方向的坐标；、和分别为叶片在局部坐标系中径向、横向位移以及剪切角；为由叶片局部坐标系向坐标系的旋转变换矩阵；为由坐标系向坐标系的旋转变换矩阵；为由旋转坐标系向固定坐标系的旋转变换矩阵。、和旋转变换矩阵的具体表达式为

(10)

(11)

(12)

式中：为叶片安装角；d为圆盘与第个叶片根部连接处的转角；b为静止状态下第个叶片在叶片组中的位置,b=2π(-1),为叶片数；ϑ为第个叶片任意时刻在固定坐标系中的位置。ϑ的具体表达式为

ϑ=+b

(13)

第个叶片在固定坐标系下的动能为

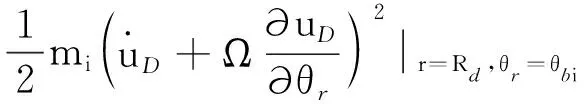
(14)

式中：、和分别为叶片的密度、截面积和长度,=,为叶片宽度,为叶片厚度；为叶片根部连接部分的质量。

第个叶片的弹性势能为

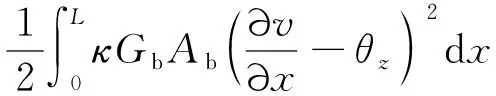
(15)

式中：、、和分别为叶片的弹性模量、剪切模量、剪切系数和截面惯性矩。

第个叶片受离心产生的势能为

(16)

式中：为叶片各个截面的离心力,表达式为

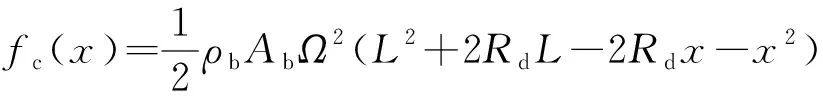
(17)

1.3 裂纹叶片建模

如图2所示,裂纹表面位移主要分为：I—裂纹张开模式,II—裂纹滑移模式和III—裂纹撕裂模式。表示在各个方向裂纹导致的附加位移,表示各个方向上裂纹受到的载荷。

根据Castigliano原理可知

=∂∂

(18)

式中：为裂纹释放的应变能,表达式为

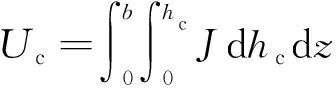
(19)

式中：为叶片裂纹的深度；为应变能密度,的表达式为

(20)

式中：I、II和III(=1,2,…,6)为3种裂纹位移模式的应力强度因子；为泊松比。由于I型裂纹是最常见和最危险的,且弯矩载荷为主要的影响因素,因此只考虑I型裂纹弯矩导致的附加应变能,其表达式为

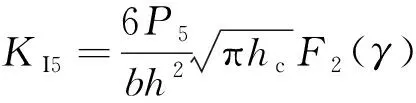
(21)

(22)

(23)

式中：为裂纹处的弯矩载荷；为与裂纹相关的几何形状修正系数。裂纹释放的应变能可表示为

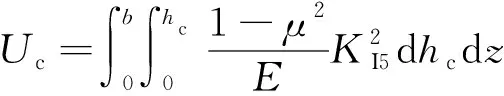
(24)

因此,可得到裂纹的局部柔度系数为

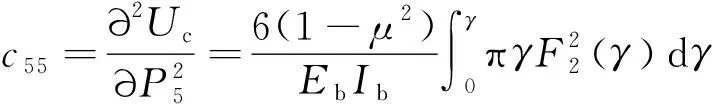
(25)

将裂纹面等效为一个旋转刚度项,具体表达式为

图2 裂纹叶片几何形状以及受力状态Fig.2 Geometrical shape and force state of cracked blade

(26)

1.4 耦合系统建模

基于Hamilton原理,将弹性轮盘以及叶片动能和势能代入

(27)

式中：为耦合系统非保守力做功。得到关于轮盘横向位移、叶片径向位移、叶片横向位移以及叶片剪切角的动力学方程。

弹性轮盘的横向位移可以表示为

(28)

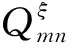
0()=cosh(-)-cos(-)+

(sinh(-)-sin(-))

(29)

(30)

式中:cosh((-))cos((-))=-1,满足轮盘内径固支,外径自由的边界条件。

健康叶片径向位移、叶片横向位移以及叶片剪切角可以表示为

(31)

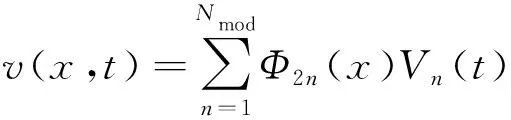
(32)

(33)

式中：、和分别为径向、横向和剪切角对应的广义坐标；1、2和3分别为径向、横向和剪切角的振型函数；为模态截断数。振型函数1、2和3具体表达式为

1()=sin()

(34)

2()=cosh ()-cos ()+(sinh ()-

sin ())

(35)

3()=′2()(π)

(36)

式中:

(37)

(38)

cosh ()cos ()=-1

(39)

裂纹叶片可以看作是内含旋转刚度的两段梁,裂纹导致每段梁在弯曲方向的振型函数发生了变化,可以假设为

sinh ()+cosh ()≤

(40)

sinh ()+cosh ()>

(41)

式中：为裂纹截面到叶片根部的距离,裂纹导致剪切角突变,振型函数需满足如下边界条件:

(42)

式中：( )′、 ( )″和( )‴分别与剪切角、弯矩和剪切力相关。

采用Galerkin方法,可以得到旋转裂纹叶片-弹性盘耦合系统离散后的运动微分方程为

(43)

式中：、、、和分别为轮盘的质量矩阵、陀螺矩阵、刚度矩阵、广义坐标向量和广义载荷向量；、、、和分别为裂纹叶片的质量矩阵、科氏力矩阵、刚度矩阵、广义坐标向量和广义载荷向量；、、、和分别为健康叶片的质量矩阵、科氏力矩阵、刚度矩阵、广义坐标向量和广义载荷向量；、和分别为叶片以及叶根连接质量导致的附加质量矩阵,附加陀螺矩阵和附加刚度矩阵；和分别为健康叶片和轮盘耦合引起的耦合质量矩阵和耦合刚度矩阵；和分别为裂纹叶片和轮盘耦合引起的耦合质量矩阵和耦合刚度矩阵。

2 模型验证

如图3所示,以叶片-弹性轮盘耦合系统为研究对象,进行了实验研究。耦合系统主要包括8个叶片和1个弹性薄圆盘,耦合系统中轮盘内径为0.02 m,轮盘外径为0.12 m,轮盘厚度为0.002 69 m,轮盘密度为7 100 kg/m,轮盘弹性模量为2×10Pa,轮盘泊松比为0.3,叶片宽度为0.03 m,叶片厚度为0.002 m,叶片长度为0.73 m,叶片安装角为30°,叶片密度为2 750 kg/m,叶片弹性模量为7×10Pa,叶片泊松比为0.33,叶片根部连接部分的质量为0.009 9 kg。

图3 叶片-弹性轮盘测试系统Fig.3 Test system of blade-flexible-disk coupling system

采用锤击法对叶片-弹性轮盘耦合系统进行了模态测试,测试系统主要包括：信号采集系统(DH5902)、KISTLER力锤(9724A2000)、PCB加速度传感器(352B10)和计算机。采用多点激励单点拾振的方法获取耦合系统的固有频率,9个激励点分布于弹性轮盘和不同叶片上,并在弹性轮盘上获取相应的振动响应。

此外,为了充分验证本文提出方法的有效性和准确性,基于ANSYS软件建立了叶片-弹性轮盘耦合系统的有限元模型,如图4所示。在有限元模型中,采用SHELL181单元模拟弹性轮盘,采用SOLID186单元模拟健康叶片和裂纹叶片,采用MASS21单元模拟叶片根部连接部位的质量；叶片根部截面节点与轮盘叶片连接面上的节点进行刚性连接；轮盘内径进行固支约束,且对圆盘节点的面内自由度进行了约束。

图4 叶片-弹性轮盘耦合系统有限元模型Fig.4 Finite element model of blade-flexible-disk coupling system

表1给出了通过实验、有限元和本文方法获得的叶片-弹性轮盘耦合系统前13阶固有频率,且为满足在相同振型下对比测试、有限元和本文方法的固有频率,对实验9～10阶固有频率进行了调整。当所有叶片为健康叶片时,本文方法与实验的最大误差小于5%,造成误差的主要原因是：实际叶片跟轮盘结构采用螺栓连接,改变了弹性盘的局部刚度以及外缘自由边界,此外,加工精度导致叶片之间厚度和长度的不一致,以及安装过程中的定位和预紧力不能保持完全一致；本文方法与有限元模型的最大误差小于5%,造成误差的主要原因是：有限元模型中叶片采用实体单元,而本文方法叶片基于Timoshenko梁理论,且轮盘叶片的连接面改变了弹性盘的局部刚度以及弹性轮盘外缘的自由边界,本文模型忽略了叶片对轮盘外径自由边界的影响。当1号叶片为裂纹叶片时,且裂纹位置=0.11,裂纹深度=0.3,本文方法和实验与有限元方法的最大误差小于5.5%,造成误差的主要原因除上述原因外还包括裂纹几何修正系数与实际裂纹之间的误差。

表1 叶片-弹性轮盘耦合系统固有频率Table 1 Natural frequencies of blade-flexible-disk coupling system

图5为叶片-弹性轮盘锤击实验获得的频响曲线,由于裂纹的引入导致部分原本重合的固有频率发生了分散,并且导致其中一阶固有频率有明显的降低,如图中、和区域所示；而理论上健康叶片-弹性轮盘本该重合的频率发生分散(如211.06 Hz和213.14 Hz、338.99 Hz和341.80 Hz)的主要是由于实验件加工和安装误差导致。

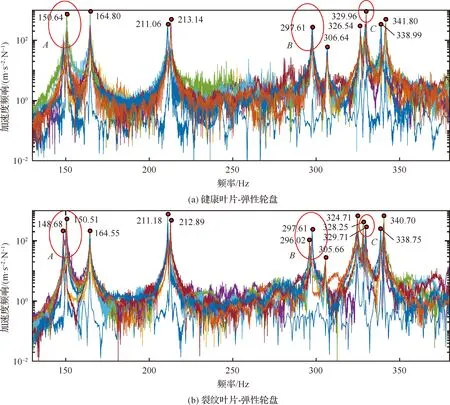
图5 叶片-弹性轮盘锤击实验频响曲线Fig.5 Frequency response curve of blade-flexible-disk coupling system by hammering test

图6和图7分别为健康叶片-弹性轮盘耦合系统和裂纹叶片-弹性轮盘耦合系统的部分振型图,实验模态中主要获取了轮盘的振型,有限元模型左下角子图为相应频率下轮盘的振型,本文方法轮盘振型用“白色”等高线描绘。由图可见,健康叶片-弹性轮盘耦合系统中,1阶和4阶模态分别以轮盘1节径和2节径占主导,第8、9、11和12阶模态以叶片弯曲占主导且分别与轮盘4节径、1节径、0节径和2节径模态耦合；裂纹叶片-弹性轮盘耦合系统中,1阶和4阶模态依旧以轮盘1节径和2节径为主导,然而由于裂纹的引入,导致与第8、9、11和12阶模态耦合的轮盘节径模态遭到破坏,以及叶片振型也发生了显著变化,且轮盘振型以1号叶片(裂纹叶片)与轮盘圆心连线为分界线对称分布。由图可见,本文方法获取的振型与实验振型及有限元方法基本吻合,验证了本文方法的有效性和准确性。实验中,部分阶次振型发生不规则的原因主要是：模态实验测试点位置不够紧密,以及实验件本身的加工精度误差、螺栓连接的影响和装配过程中预紧力的影响等。需要说明的是,本文中取值为6,取值为4,叶片数为8,耦合系统整体自由度为2×+×=44,有限元模型中健康叶片-轮盘耦合系统自由度为171 624以及裂纹叶片-轮盘耦合系统自由度为171 522；求解44阶固有频率,在ANSYS中计算时间约为99 s,本文方法计算时间约为28 s,计算效率提升明显。

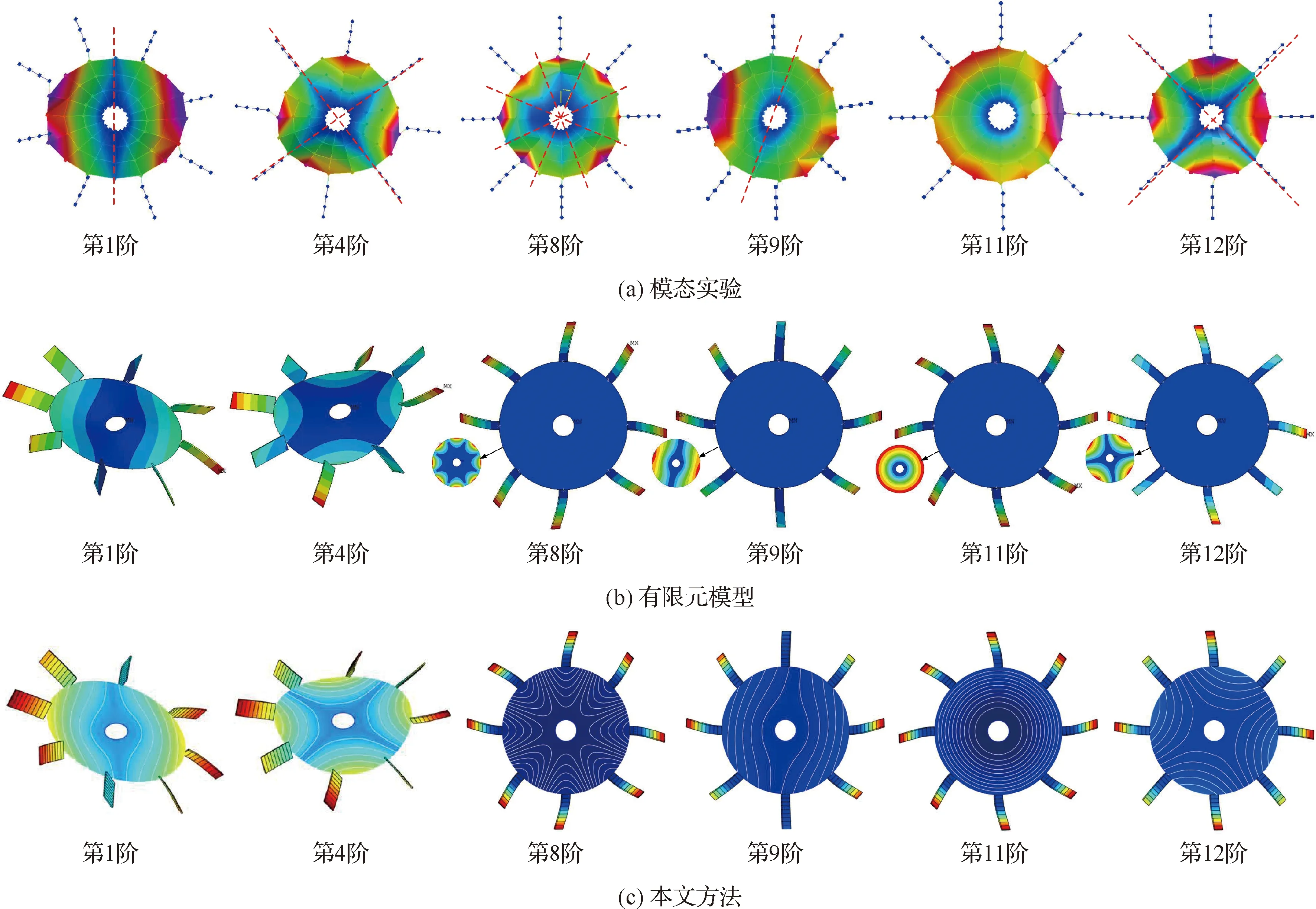
图6 健康叶片-弹性轮盘耦合系统振型图Fig.6 Mode shapes of healthy-blade-flexible-disk coupling system

图7 裂纹叶片-弹性轮盘耦合系统振型图Fig.7 Mode shapes of crack-blade-flexible-disk coupling system

图8为叶片-弹性轮盘耦合系统前13阶的模态置信度(MAC)值,从图8(a)中可以看出,健康叶片-弹性轮盘耦合系统在非对角线上出现非0的MAC值,例如(9,1)和(12,4)位置有较大的MAC值,说明第9阶和第1阶模态、第12阶模态和第4阶模态具有相关性,这与图6中显示耦合系统振型一致；从图8(b)中可以看出,裂纹叶片-弹性轮盘耦合系统在非对角线位置出现更多的MAC值,与健康叶片耦合系统相比,与第6、9、11和12阶相关的MAC值发生明显的变化,这与图7中第9、11和12阶振型与健康叶片耦合系统相比发生明显的变化结论一致,此外,表1中对应阶次的固有频率与健康叶片耦合系统相比也有明显的降低。

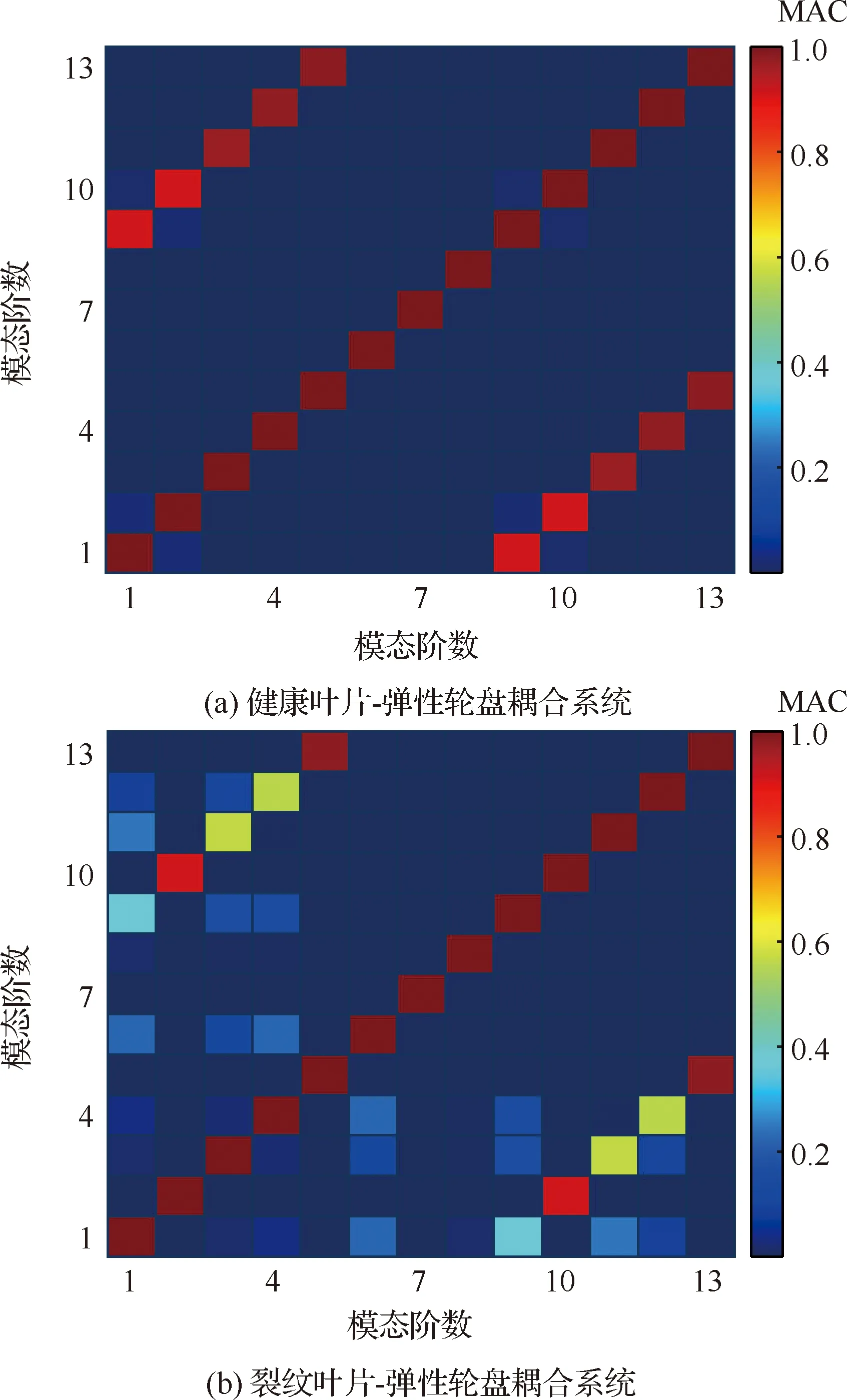
图8 叶片-弹性轮盘耦合系统前13阶模态MAC值Fig.8 MAC values for the first 13 orders mode of blade-flexible-disk system

图9为轮盘厚度=0.2时不同转速下健康叶片-弹性轮盘耦合系统的固有频率变化曲线。需要说明的是,在ANSYS平台中不能同时考虑轮盘的陀螺效应和叶片科氏力、离心钢化以及旋转软化,因此在图9(a)中对比了不考虑轮盘陀螺效应时的固有频率变化曲线,由图可知,随着转速的增加旋转叶片和弹性轮盘的固有频率逐渐增大,且叶片固有频率增大更加明显,并在交汇处发生了振型转换现象,由低转速下第9阶为轮盘1节径模态转换为高转速下第1阶为轮盘1节径模态。本文方法和有限元方法结果吻合较好,进一步验证了考虑旋转效应后本文方法的有效性。图9(b)为考虑轮盘陀螺效应后系统的固有频率变化曲线,由于考虑了弹性轮盘的陀螺效应的影响,随着转速的增大,轮盘1节径、2节径和3节径固有频率发生分叉,且在与其余模态汇交处(转速～)多次发生了频率转向和振型转换现象,这与文献[18]中的结论类似,更加说明了在叶盘结构中考虑轮盘弹性变形是非常必要的。

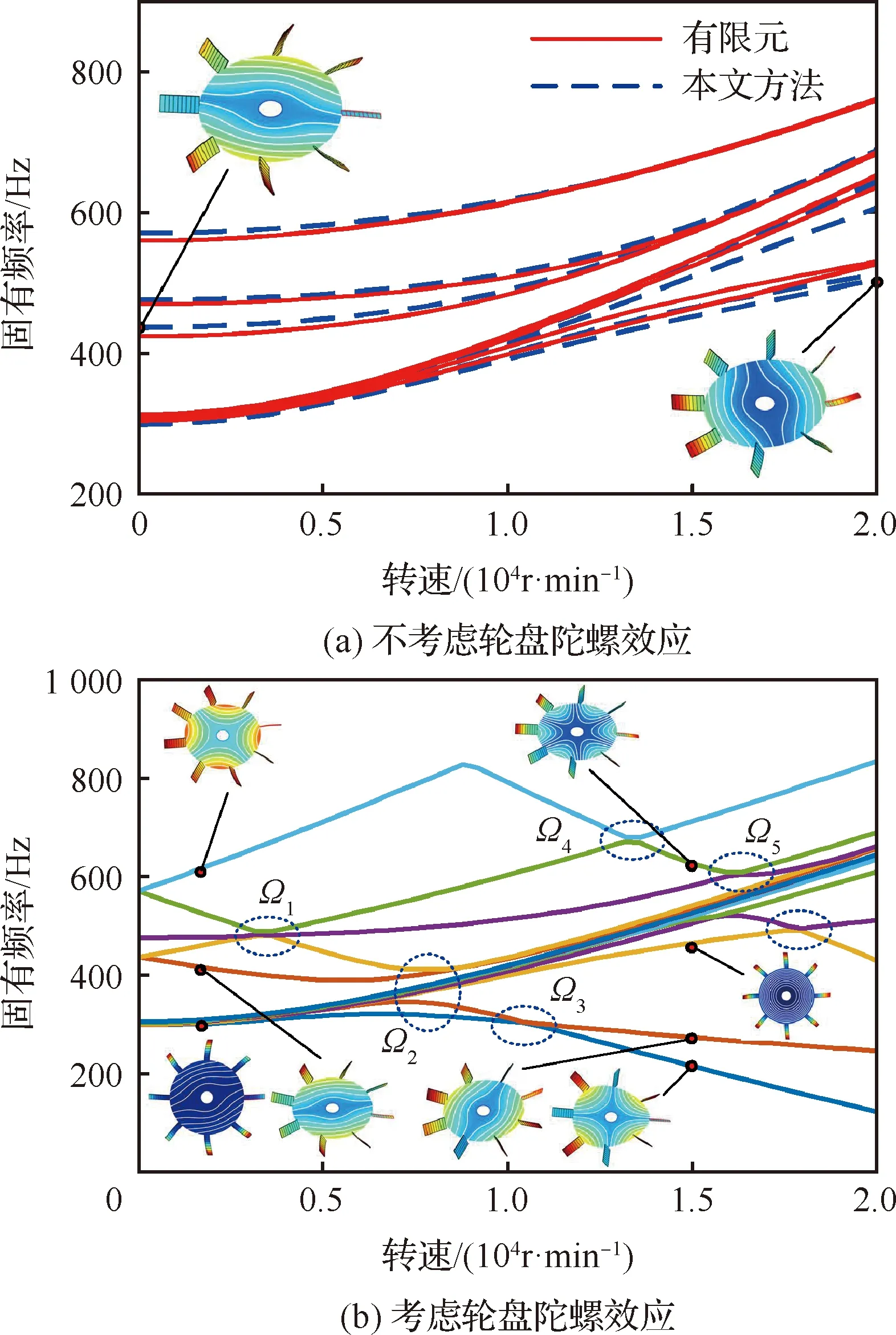
图9 不同转速下健康叶片-弹性轮盘耦合系统固有频率变化曲线Fig.9 Variation curves of natural frequencies of healthy-blade-flexible-disk coupling system with different rotational speed

3 系统振动特性分析

连续体模型力学机理明晰、物理可解释性强、计算效率高,能够有效揭示裂纹叶片的故障机理和动力学演化规律。基于本文提出的方法,以现有实验件(见图3)为研究对象,分析裂纹深度、裂纹位置、轮盘厚度和旋转速度对旋转裂纹叶片-弹性轮盘耦合系统振动特性的影响。

3.1 裂纹深度对固有特性的影响

由于本文方法只考虑轮盘内径固支边界导致的节圆,以及叶片的弯曲振型,为了更好地标识耦合系统各阶模态振型,分别用、和标识节径轮盘模态、叶片阶弯曲和节径轮盘耦合模态以及裂纹对叶片阶弯曲和节径轮盘耦合振型破坏后的模态。图10为不同裂纹深度下裂纹叶片-弹性轮盘耦合系统的固有频率变化曲线图,模型中无量纲裂纹深度=/取值范围为[0,0.5],裂纹位置=0.1。

图10 不同裂纹深度下耦合系统固有频率变化曲线Fig.10 Variation curves of natural frequencies of coupling system with different crack length

由图可见,裂纹深度为0(健康叶片)时、和各有2阶重合的模态,随着裂纹深度的增加,重合模态中的一阶模态固有频率不断减小,且-、-频率变化较为明显,非重合模态-和-以及重合模态中-频率略有减小,从表1中也可以看到一致的结论,此外,振型主要为裂纹叶片弯曲模态,发生模态局部化现象。

3.2 裂纹位置对固有特性的影响

图11为不同裂纹位置下裂纹叶片-弹性轮盘耦合系统固有频率变化曲线,模型中无量纲裂纹位置=/取值范围为[0.1,0.9],裂纹深度=0.4。由图可见,随着无量纲裂纹位置的增大(裂纹位置越靠近叶尖),分散的固有频率逐渐靠近,例如和、和以及和,且和固有频率变化明显,、和固有频率略有增大。此外,从和的振型图中可以看出,耦合系统中的轮盘振型以1号叶片(裂纹叶片)与轮盘圆心连线为分界线对称分布,且靠近叶尖位置裂纹叶片模态局部化现象消失,两阶模态形成正交模态。

图11 不同裂纹位置下耦合系统固有频率变化曲线Fig.11 Variation curves of natural frequencies of coupling system with different crack position

3.3 轮盘厚度对固有特性的影响

图12为不同轮盘厚度下裂纹叶片-弹性轮盘耦合系统固有频率变化曲线,模型中无量纲轮盘厚度=/取值范围为[0.08,0.25],裂纹深度=0.1,裂纹位置=0.4。由图可见,随着轮盘厚度的增大,发生了振型转换的现象,即薄轮盘下前5阶为与轮盘相关的模态转换成厚轮盘下后5阶为与轮盘相关的模态；且薄轮盘下第1阶次与叶片弯曲相关的模态为,而在厚轮盘下第1阶次与叶片弯曲相关的模态改变为,与叶片弯曲相关的其余模态随着轮盘厚度的增加固有频率越来越靠近。

图12 不同轮盘厚度下耦合系统固有频率变化曲线Fig.12 Variation curves of natural frequencies of coupling system with different disk thickness

图13为无量纲轮盘厚度=0.2时前13阶耦合系统的MAC值,由图可见,在非对角线上出现了许多非零值,第1阶模态与第9阶模态(模态)相关,第6阶模态与第12阶(模态)相关,这与图12中结论一致；且第3阶模态和第4阶模态与多阶模态相关,从图12(b)中也可以看出第3阶和第4阶轮盘振型更加复杂,且与多个轮盘节径模态相关。

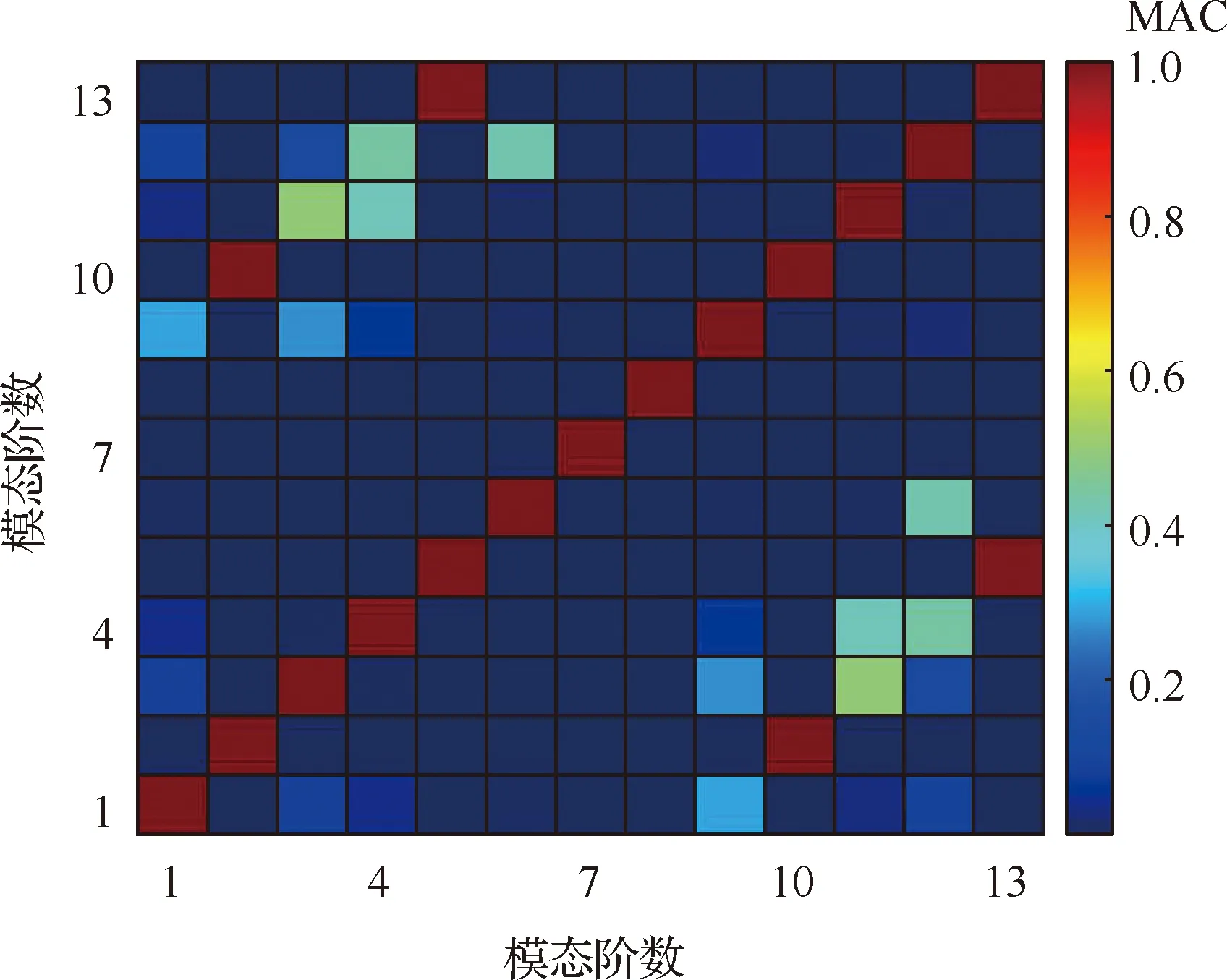
图13 耦合系统前13阶模态MAC值(ξD=0.2)Fig.13 MAC values for the first 13 orders mode of coupling system (ξD=0.2)

3.4 旋转速度对固有特性的影响

图14为不同转速下裂纹叶片-弹性轮盘耦合系统固有频率变化曲线,模型中转速取值范围为[0, 20 000] r/min,裂纹深度=0.1,裂纹位置=0.4,轮盘厚度=0.2。与健康叶片-弹性轮盘相同(见图9),由于考虑了弹性轮盘的陀螺效应和离心力以及叶片离心力、科氏力和旋转软化的影响,在模态汇交处(转速～)发生了频率转向和振型转换现象,且由于裂纹的影响,裂纹叶片-弹性轮盘第1阶固有频率(叶片弯曲主导模态且与轮盘1节径耦合)与健康叶片-弹性轮盘对比,在低转速下明显降低。

图14 不同转速下耦合系统固有频率变化曲线Fig.14 Variation curves of natural frequencies of coupling system with different rotational speed

为进一步分析转速对裂纹的影响,对比了振型转换之前(转速之前,见图14)健康叶片-弹性轮盘和裂纹叶片-弹性轮盘第1阶固有频率(叶片主导模态)的变化曲线,如图15所示。由图中可以看出,离心力导致的刚化效应,使得健康叶盘和裂纹叶盘的固有频率均增大。然而随着转速的增加,裂纹叶盘与健康叶盘的相对误差的绝对值越来越小,表明离心刚化对裂纹叶盘的影响更加明显。

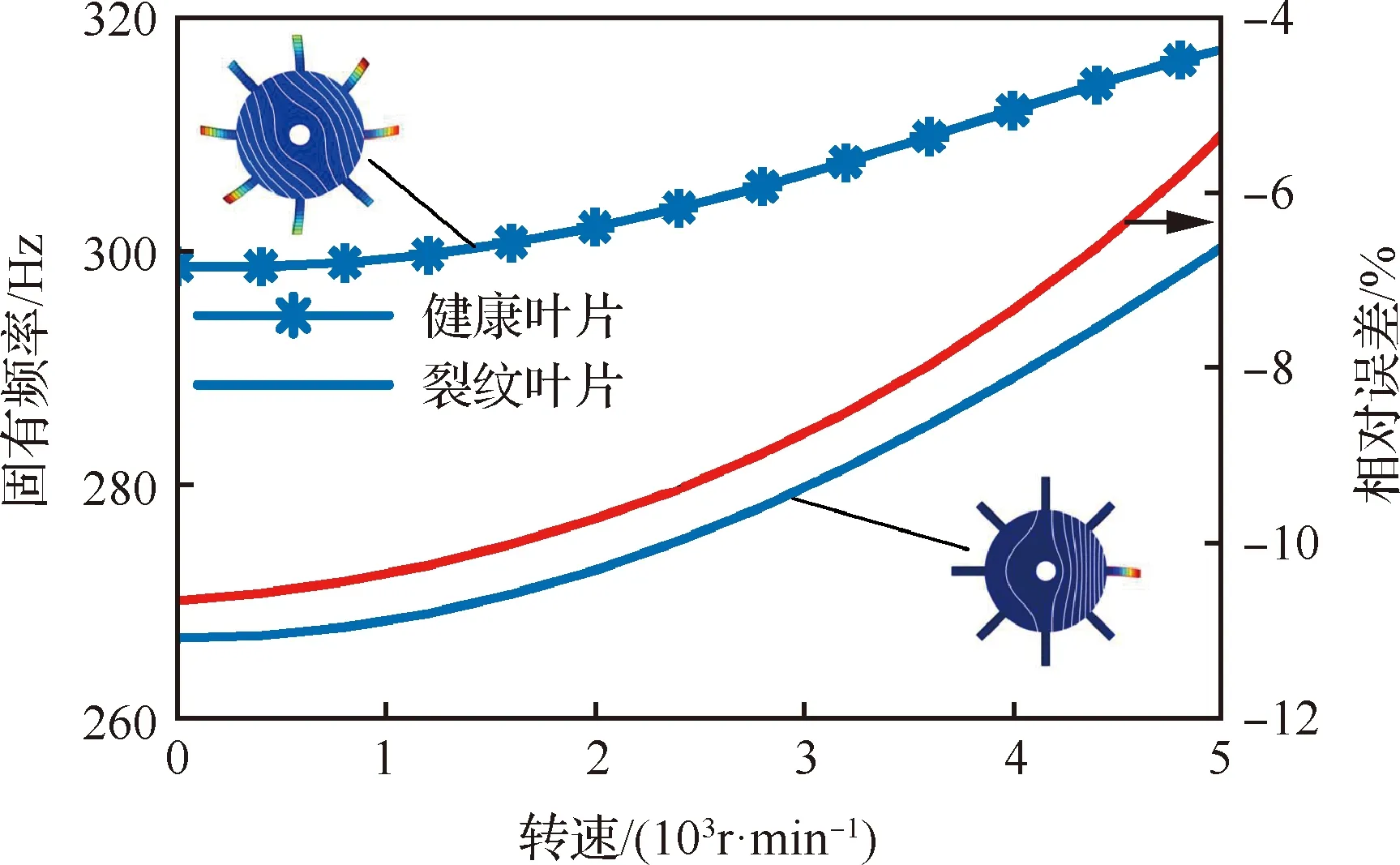
图15 不同转速下健康和裂纹叶盘固有频率变化曲线Fig.15 Variation curves of natural frequencies of healthy and crack blisk with different rotational speed

图16为不同转速下耦合系统前13阶MAC值,转速为1 600 r/min时,第1～8阶为叶片弯曲主导的模态,第9～13阶为轮盘节径主导模态；转速为15 000 r/min时,第3～10阶为叶片弯曲主导模态,其余阶次为轮盘节径主导模态。由图可以看出,在1 600 r/min下非对角线非零MAC值出现的位置较为聚集,第1～8阶模态(叶片主导模态)与轮盘节径模态有关；在15 000 r/min 下非对角线非零MAC值出现位置杂乱无序,第3～10阶模态(叶片主导模态)除了与轮盘节径模态有关外,还与其他叶片主导的模态相关,说明由于旋转效应使得耦合系统模态变得更加复杂。