航空发动机导叶控制机构作动筒主动容错控制

杨晓伟,葛曜文,邓文翔,姚建勇,周宁

南京理工大学 机械工程学院,南京 210094

随着理论发展与技术革新,以经典反馈控制为主体的电液伺服控制技术逐渐发展成综合液压技术、电气技术与控制理论为一体的自动化技术。由于输出力/力矩大、功重比输出高、快速响应及自润滑等特点,电液伺服控制系统被广泛应用在航空、航天以及民用工程等自动化控制领域。近些年,国内外航空发动机导叶控制系统得到了飞速发展,导叶控制方式从传统的机械液压控制方式转变为先进的电子+机械液压混合控制方式。航空发动机导叶控制机构液压作动筒上的位置伺服控制是电液伺服系统的典型应用。导叶控制机构液压作动筒伺服系统由电液伺服阀、液压作动筒、叶片和位移传感器等组成。其中液压作动筒主要作用是驱使航空发动机导叶控制机构正常运作,从而调节航空发动机内外涵道进气量,扩大喘振裕度,保证发动机稳定工作。

为了适应航空发动机在高速、高温、变载荷等极端条件下运行安全的需求,这就需要航空发动机导叶控制机构液压作动筒在发生故障时仍能正常供给航空发动机内外涵道进气量,从而保证航空发动机稳定工作。因此,这就对其容错能力、抗干扰能力以及控制性能提出更高的要求。

导叶控制机构液压作动筒在高速、高温、变载荷等条件下的故障模式主要包括外力突增、密封失效、物理参数突变等。工作在变载荷下的液压作动筒易发生外力突增,从而使筒体所受外干扰变大,影响导叶控制机构正常工作；高速条件下引起的密封失效会带来油液污染；在高速、高温、变载荷等恶劣环境下,液压作动筒的实际物理参数由于温度快速升高以及摩擦加大发生突变,例如液压作动筒活塞杆粘性系数会由于高温急剧变化,作动筒内泄漏系数也会由于高速、变载荷下因密封失效、泄漏增大而发生变化等等。为及时监测导叶控制机构液压作动筒上的故障,确保航空发动机运行安全,针对液压作动筒在高速、高温、变载荷等条件下设计主动容错控制是必不可少的。

目前关于航空发动机导叶控制机构液压作动筒容错控制文献比较少,但为了适应航空发动机在高速、高温、变载荷等条件下运行安全的需求,这就对液压作动筒的容错能力提出更高的要求。为确保液压作动筒在在高速、高温、变载荷等条件下发生故障时仍能实现高性能位置跟踪控制以及主动容错,提出一种积分鲁棒自适应主动容错控制策略。针对液压作动筒在高速、高温、变载荷下产生的参数突变的不确定性,基于Lyapunov理论发展了一种基于参数估计误差与跟踪误差的复合参数自适应律。该参数自适应律确保了参数的快速收敛。为抵抗参数不确定性与高速变载荷引起的外干扰故障对系统的影响,将积分鲁棒控制与参数自适应方法相结合,发展了一种积分鲁棒自适应主动容错控制,进一步提高了液压作动筒的容错能力与位置跟踪能力,实现了在高速、高温、变载荷等条件下发生故障时系统位置跟踪的渐近收敛性能。

1 问题描述与数学建模

某型航空发动机导叶控制机构工作原理如图1所示,它将双喷嘴挡板力反馈两级流量控制电液伺服阀、液压作动筒、叶片和LVDT位移传感器等集成为一体,是典型的电液位置控制系统。正常工作时,电液伺服阀通过控制液压作动筒两腔流量来调节两腔的压力大小,从而控制作动筒活塞杆的伸出长度。由于作动筒活塞杆伸出端与叶片通过连杆铰接在一起,叶片的角度随着作动筒活塞杆位移变化而变化,从而调节航空发动机内外涵道进气量,扩大喘振裕度,保证航空发动机稳定工作。

图1 航空发动机导叶控制机构工作原理图Fig.1 Working principle architecture of guide vane control mechanism of aeroengine

在图1中,研究对象为液压作动筒；和分别表示LVDT位移传感器测的水平位移以及液压作动筒的水平运动位移；表示电液伺服阀控制输入；和分别表示液压缸左右两腔的油压；和分别表示液压缸供油压力和回油压力；和分别表示活塞杆两端的有效作用面积；和分别表示液压缸的供油流量与回油流量；和分别表示连杆上活塞杆的铰接处与LVDT铰接处的距离以及LVDT铰接处与连杆固定转轴的距离。

考虑图1中的连杆几何关系,作动筒活塞杆的水平位移与位移传感器测得水平位移成定比例关系,满足=(1+),即通过位移传感测得值可解算得到液压缸活塞杆的实际位移,从而可以通过控制液压作动筒的位移来控制叶片角度。因此,考虑的航空发动机导叶控制机构液压作动筒伺服控制原理如图2所示。基于图1与图2,根据牛顿运动学定律可得液压作动筒惯性负载的动力学方程为

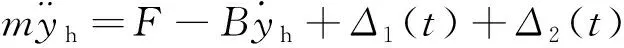
(1)

式中：表示与液压作动筒伸出端铰接的连杆的等效惯性质量；=-表示液压缸的负载力；表示液压缸的粘性阻尼系数；()表示系统的常值干扰；()表示系统的未建模干扰,包括外干扰、未建模动态以及未建模摩擦等。

考虑油液可压缩性,忽略压力未建模动态,则液压缸两腔的压力动态方程可表示为

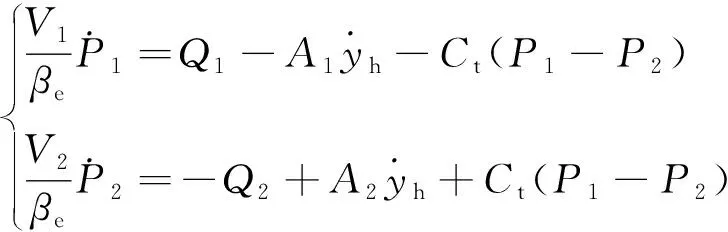
(2)

式中：=+和=-表示液压缸两腔的容积,和表示活塞杆处于液压缸初始位置时两腔的起始容积；表示油液有效弹性模量；表示液压缸内泄漏系数。

图2 航空发动机导叶控制机构液压作动筒伺服控制图Fig.2 Servo control diagram of hydraulic actuating cylinder of guide vane control mechanism of aeroengine

考虑电液伺服阀频宽远高于系统其他部分的频宽,因而可忽略电液伺服阀的阀动态,则其流量方程为

(3)

式中：表示电液伺服阀流量增益系数；函数sng()表示为

(4)

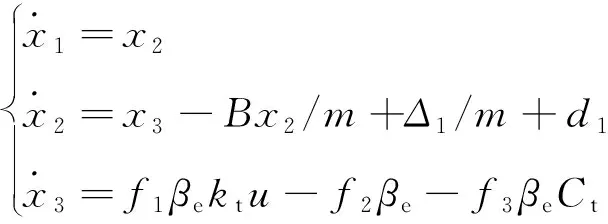
(5)

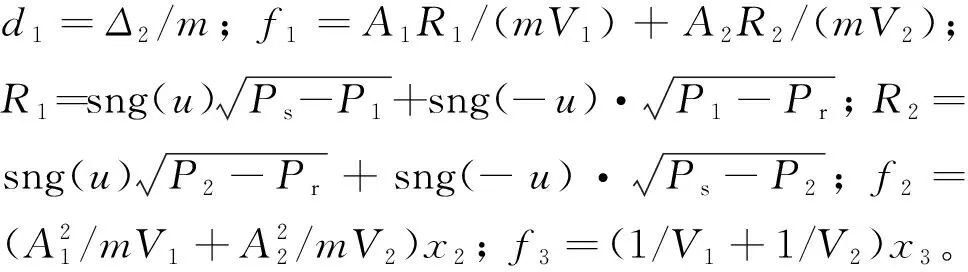
2 主动容错控制设计

考虑航空发动机导叶控制机构液压作动筒在高速、高温、变载荷等极端条件下出现故障问题时,其系统内一些物理参数会发生明显变化。例如,液压缸内温度急剧变化或外干扰突然增大时,参数或会突变；液压缸密封部分失效时,参数会突变；油液温度升高时,参数会突变等等。为方便液压作动筒出现故障时及时定位故障原因,物理参数的实时在线更新是一个有效的方法。因此,定义参数向量=[,,,,],其中=,=,=,=以及=。此时,式(5)可表示为

(6)

设计液压作动筒主动容错控制策略前,假设：

2) 时变干扰是3阶可导。

3) 被定义的参数向量满足：

∈={:min≤≤max,=1,2,…,5}

(7)

2.1 参数自适应设计

基于式(7),定义一个不连续映射为

(8)

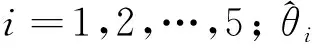
(9)

则不连续映射式(8)具有属性：

(10)

为设计参数自适应律,重新构建式(6)为

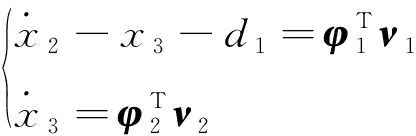
(11)

式中：=[-/, 1/];=[, -, -];=[,];=[,,]。

对式(11)两侧进行一阶滤波,可得：

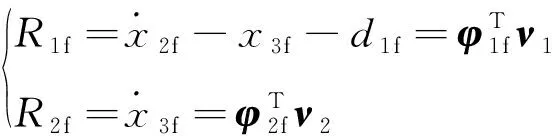
(12)

其中：

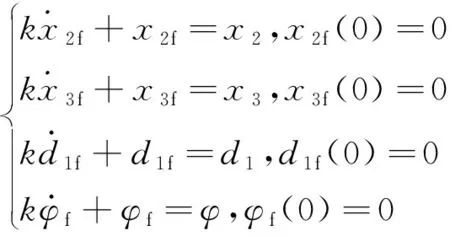
(13)

式中：=[,];>0表示一阶滤波系数; (·)表示·一阶滤波的输出。

定义变量：

(14)

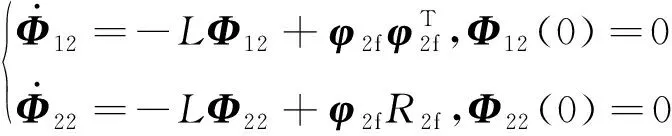
(15)

式中：>0表示变量衰减因子系数。

则式(14)与式(15)的解为

(16)

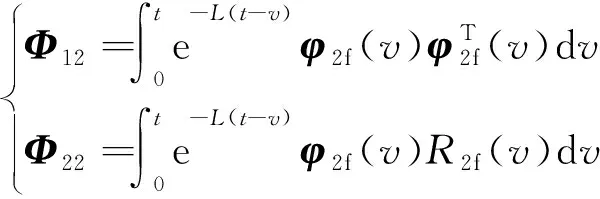
(17)

根据式(16)与式(17),可得：

(18)

值得注意的是：经过前文一系列滤波变换和变量定义,最终利用系统的已知信息表示出系统的未知参数。因此,可设计参数自适应律为

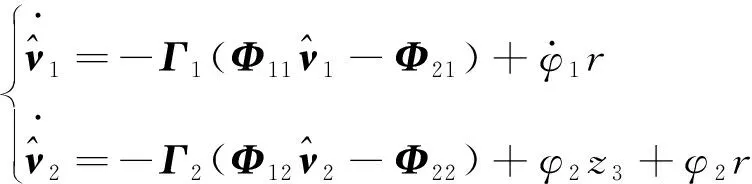
(19)

式中：和表示正的对角矩阵；随后定义变量。参数自适应律式(19)由两部分构成：基于参数估计的误差和系统的跟踪误差。这样设计既可提高参数的收敛速度和系统的主动容错能力,又可提高系统的跟踪精度与鲁棒能力。

2.2 控制器设计

定义变量：

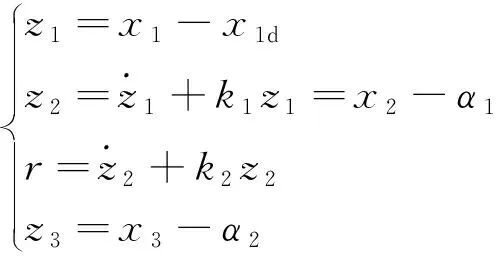
(20)

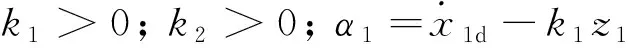
结合式(6)和式(20),可得:

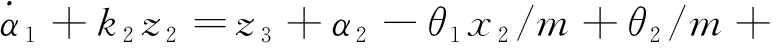
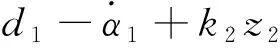
(21)

基于式(21),虚拟控制律为

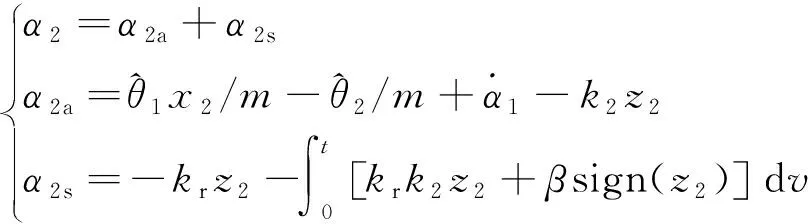
(22)

式中：>0;>0;表示模型的补偿项；表示线性反馈项与非线性反馈项的组合,目的是镇定系统稳定；函数sign()表示标准的符号函数。

将式(22)代入式(21),可得

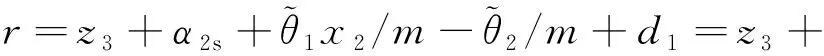
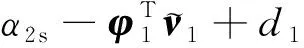
(23)

对式(23)两侧同时微分,得

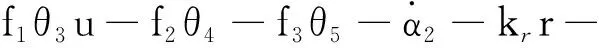
(24)

基于式(24),可设计系统的控制律：

(25)

式中：>0;表示模型的补偿项；表示线性反馈项,目的是镇定系统稳定。

将式(25)代入式(24),可得的动态性能：

(26)

进一步,可得的动态性能为

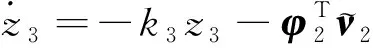
(27)

2.3 稳定性分析

为便于主动容错控制器的稳定性分析,给出引理：

：定义变量()与()为

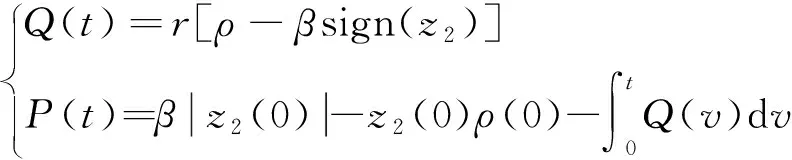
(28)

如果增益满足：

>+

(29)

则()>0始终成立。

：见参考文献[14-16]。

：基于参数自适应律式(19)与控制律式(25),通过选取合适的增益、、、、、和,使得矩阵

(30)

为正定矩阵,则所有的系统信号都是有界的,且系统的跟踪误差能够渐近收敛到0。

证明：选取Lyapunov函数为

(31)

根据引理1可得,式(31)恒为正,则

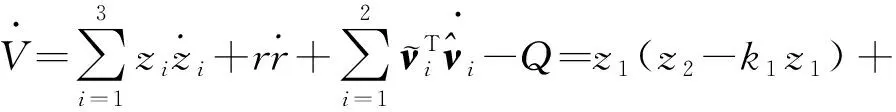
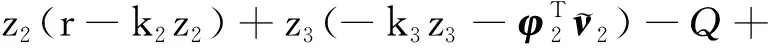
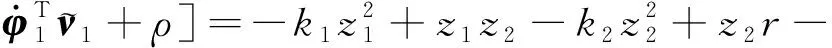
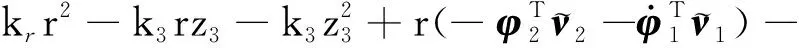
(32)

定义=[;;;],结合设计的参数自适应律式(19)和式(30),可得：

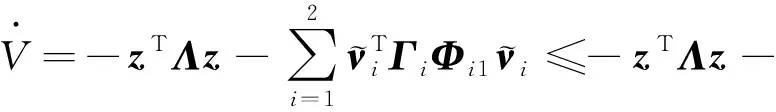
(33)

式中：(·)表示·的最小特征值。

由式(33)可得∀>0,()<(0),由此可知有界,即有界,系统的所有信号都是有界的。对式(33)两侧进行积分,可得：

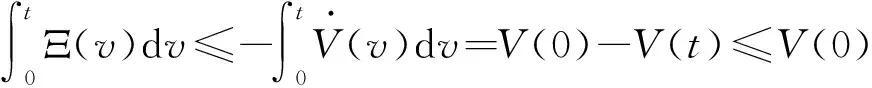
(34)

根据式(34),Ξ是有界的,又基于式(19)与式(20),Ξ的导数是有界的,因此由Barbalat引理可知：当→∞时,Ξ→0,即→0,则系统的跟踪误差→0,因此证明了定理1。

3 仿真验证

某型航空发动机导叶控制机构液压作动筒控制系统的物理仿真参数选取如下：=40 kg,/=1,=50 N(m·s),=25×10m,=2×10m,==1×10m,=7×10m/(s·Pa),=200 MPa,=925×10m/(s·V·Pa),=0 N,=0.05 sin(),=7 MPa,=0 MPa。

为验证提出的积分鲁棒自适应主动容错控制的有效性,针对下列3种控制器进行仿真对比。

2) REF是不含自适应的积分鲁棒容错控制器。与AREF区别就是该容错控制器的物理参数始终保持不变,即参数自适应增益矩阵为=diag(0,0)和=diag(0,0,0),其他控制器参数与AREF一样。

3) RCF是非线性鲁棒容错控制器。该控制器物理参数始终保持不变,控制器参数被选取为：=200,=50,=10。

仿真包括以下3种工况：

工况1：液压作动筒正常工作。在这种无故障工况下,如图3所示的期望跟踪曲线=01sin()(1-e-001) rad被用来验证3种容错控制器的有效性。由图4的3种容错控制器跟踪误差可知,提出的积分鲁棒自适应主动容错控制器获得最好的跟踪性能。相比与REF和RCF的10rad级别的跟踪误差,AREF的稳态跟踪误差达到10rad级别。这是因为整合参数自适应律与积分鲁棒反馈的AREF既可以利用参数自适应律实时在线的更新参数,又可以利用积分鲁棒反馈去提高系统的容错能力,从而进一步提高系统的跟踪误差的精度。尽管REF由于不具有参数实时更新的能力,跟踪精度比AREF更差,但是由于具有与AREF一样的积分鲁棒反馈项,其跟踪效果比RCF要好,稳态跟踪误差与RCF相比减小了26.3%。这也分别验证了参数实时更新策略与积分鲁棒反馈的有效性。由图5的AREF的参数自适应结果可知,自适应参数在7 s左右就趋向于各自的真实值,这也揭示了提出的参数自适应方法的可靠性与快速收敛性。

图3 工况1期望跟踪曲线Fig.3 Desired tracking trajectory in Case 1

图4 工况1容错控制器跟踪误差Fig.4 Tracking errors of fault-tolerant controller in Case 1

工况2：液压作动筒工作到20 s后,由于温度急剧变化而导致粘性摩擦系数突变,估计参数为

图5 工况1 AREF参数自适应结果Fig.5 Results of AREF parameter adaptation in Case 1

(35)

其他参数保持不变。在这种粘性摩擦系数变大的故障工况下,继续用图3的期望跟踪曲线验证3种容错控制器的作用。由图6的3种容错控制器跟踪误差可知,与REF和RCF相比,AREF仍获得最佳的跟踪性能。在此种故障工况下,AREF的稳态跟踪误差仍能达到10rad级别。虽然液压作动筒运行到20 s后出现故障,系统的粘性摩擦系数发生突变,可由于AREF具有实时在线更新参数的能力,即使参数发生突变,图7的参数自适应结果显示参数的估计值在突变后5 s 左右趋向于它的突变值,其他的参数保持不变。这验证了主动容错控制策略的有效性。根据参数自适应的结果,很容易判断摩擦系数发生突变。

工况3：液压作动筒运行到20 s后出现密封失效,此时液压缸内泄漏系数急剧增大,参数取值为

图6 工况2容错控制器跟踪误差Fig.6 Tracking errors of fault-tolerant controller in Case 2

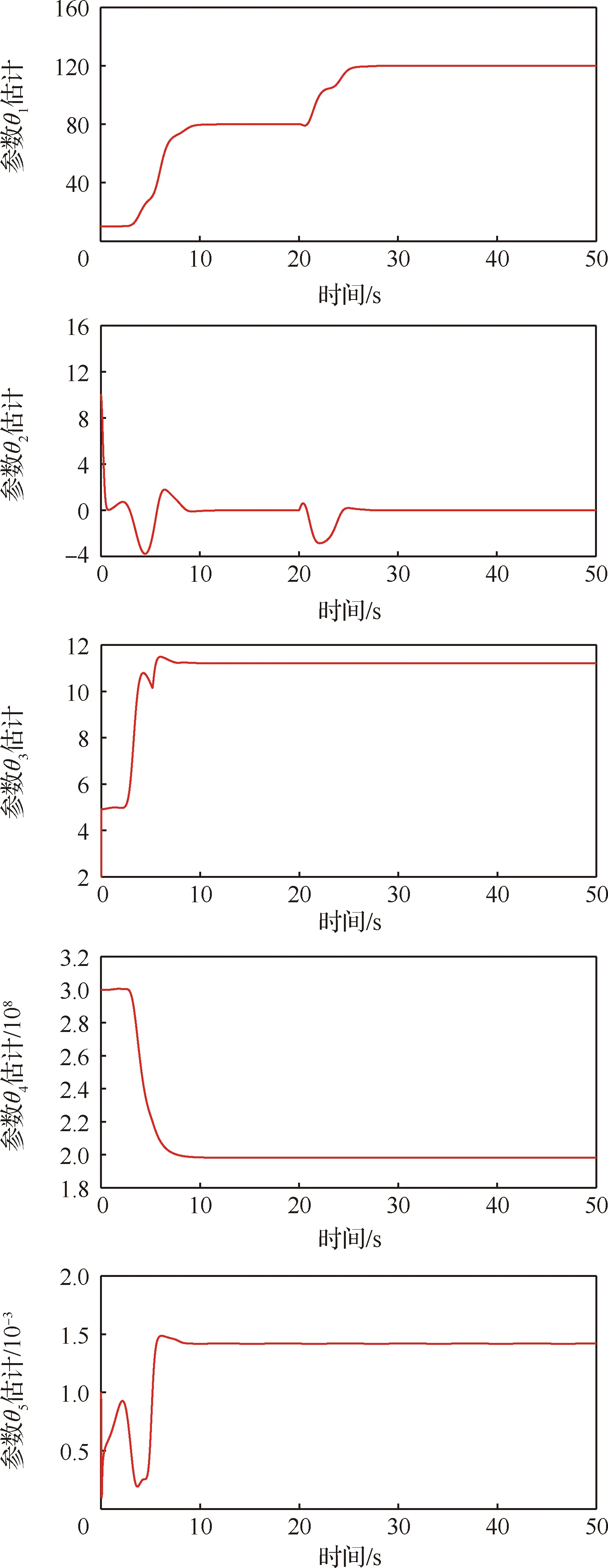
图7 工况2 AREF参数自适应结果Fig.7 Results of AREF parameter adaptation in Case 2

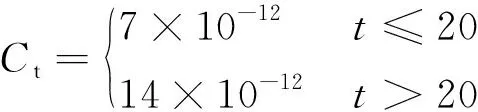
(36)

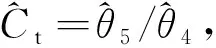
图8 工况3容错控制器跟踪误差Fig.8 Tracking errors of fault-tolerant controller in Case 3

图9 工况3 AREF内泄漏系数自适应结果Fig.9 Results of AREF internal leakage coefficient adaptation in Case 3

4 结 论

1) 通过整合参数自适应控制与积分鲁棒反馈,一种新的积分鲁棒自适应主动容错控制可保证系统跟踪误差在外干扰存在条件下渐近收敛,增强了系统的容错能力与鲁棒能力。

2) 基于参数估计误差与跟踪误差的复合参数自适应律确保了估计的参数可在7 s内快速收敛,进一步提高了系统的主动容错能力与跟踪性能。

3) 通过对比仿真,验证了积分鲁棒自适应主动容错控制策略的有效性,对保证航空发动机在复杂条件下运行安全具有一定的参考价值。同时该主动容错控制策略也可推广到其他机电液伺服领域,进行伺服系统的故障检测与主动容错,这大大拓展了该方法的使用前景。