基于混合特征与PSO-SVM的旋转部件故障诊断方法
2022-10-11何爱民孙义忠石万凯
张 拓,余 何,何爱民,孙义忠,石万凯
(1.重庆大学 机械传动国家重点实验室, 重庆 400044;2.南京高速齿轮制造有限公司, 南京 211100)
0 引言
旋转部件在航空航天、冶金、汽车、制造等领域有广泛的应用,一旦发生故障,轻则导致产品质量下降,重则引发重大事故并造成巨大经济损失[1-3]。而滚动轴承作为旋转部件的重要组成部分,其故障是造成旋转部件故障最主要的原因[4-5]。如果能对通过采集数据对设备进行实时检测,及时发现设备故障,便可准确的对设备进行干预和维护,减少事故的发生几率,降低维护成本。因此,故障诊断对设备高效运行降低维护成本有重要的意义。
目前,在故障诊断方面,基于振动信号特征信息是旋转部件故障诊断的主要方式[6-8]。Vakharia等[9]采用交叉验证技术对随机森林分类器进行优化,有效的提高了轴承故障诊断的分类精度。张例宏等[10]利用会议制随机森林算法对电机滚动轴承不同故障程度进行识别。石志炜等[11]提取滚动轴承振动信号的时域、频域、小波包节点能量等特征建立了滚动轴承故障诊断模型。孙晋锰等[12]对C4.5、Cart、BP和SVM等分类算法的准确度进行了比较,发现SVM的准确度要优于其他三种算法。在特征提取方面,曾杰等[13]利用信息增益算法对影响谐波电流发射特征的主要因素进行评估,进而识别出主要影响因素。韩卫宇等[14]运用马田系统对振动信号信息进行特征降维处理,提高了模型计算效率。
尽管振动信号特征信息可以反映部件的故障信息,但为了更全面的提取部件的故障特征信息,提高模型的识别精度,提出了一种综合考虑部件运行过程中电流和振动信息的基于混合特征和PSO-SVM的故障诊断方法。在故障特征信息提取方面,利用信息增益算法提取了对设备故障相对敏感的特征参数作为敏感特征集,并结合主成分分析对敏感特征集进行降维处理,消除了无关特征和冗余特征对模型的干扰;在故障诊断模型方面,以SVM分类器为基础,利用粒子群优化算法寻找全局最优参数,提高了模型识别精度,并借助轴承加速疲劳试验数据集与常用的故障诊断模型进行了对比,结果表明PSO-SVN模型具有更高的识别准确率,有一定的优越性。
1 混合特征向量提取
当设备发生故障时,电流信号和振动信号的某些特征会发生相应的变化,利用这些特征可以有效的识别设备的运行状态。
1.1 电流信号特征提取
由于轴承健康状态发生变化,导致驱动电机的负载发生波动,电流信号也随之波动,由于数据集数据通过封闭试验台采集,外部因素对试验数据影响较小,故认为电流的波动由负载变化引起,而不考虑电网或用电波峰波谷等外部因素对电流变化的影响。根据电流时域波形中隐含的信号[15],如绝对幅值、最大值、最小值等,可以对轴承的健康状态进行评估,各采样阶段采集电流信号为I=[i1,i2,…,iN],电流指标如表1所示。

表1 电流信号特征参数
1.2 振动信号特征提取
随着轴承故障的加剧,其振动信息也发生变化,在振动信号中隐含多种指标,如均值、方差、均方根幅值、斜度、峭度、频率方差、重心频率等,根据这些参数趋势的变化,可以对轴承的状态进行评估,并用于故障诊断[16-17]。从时域和时域的角度对传感器采集的振动信号进行特征参数提取,如表2所示,共提取27个特征参数,其中14个特征(p1—p14)为时域统计特征参数,13个特征(p15—p27)为频域统计特征参数。
各采样时间段内采集的振动信号序列为x=[x1,x2,…,xN],其中,N表示振动信号的每个样本点数。sk为信号xt的谱函数,k∈[1,K],K为谱线数;kf代表第k条谱线的频率值。参数p1和p2-p7表示时域信号的振幅和能量;参数p2和p8-p13表示时域信号的时间序列分布;参数p14表示时域信号的离散程度。参数p15表示频域中的振动能量。参数p16-p18、p20和p24-p27描述频谱功率的收敛程度。参数p19和p21-p23表示主频的位置变化。

表2 振动信号特征参数
1.3 混合特征选择与融合
为提高模型故障诊断识别率,需要提取对轴承故障状态相对敏感的特征参数。信息增益表示在已知特征参数Fpi(A1,…,A11,p1,…,p27)的信息判断部件故障类别(健康、内圈故障、外圈故障)不确定性的减少程度,特征参数Fpi对应的信息增益越大,则表示该特征参数对轴承的健康状态越敏感,故可利用信息增益指标来量化各特征参数对轴承健康状态敏感程度。
定义特征参数Fpi对数据集D的信息增益为IGpi,数据集D的经验熵为E(D),特征参数Fpi在给定条件下D的经验条件熵为D(D|Fpi),则信息增益可表示为[13,18]:
IGpi=E(D)-D(D|Fpi)
(1)
(2)
(3)
式中:Ck表示样本类别;|D|和|Ck|分别表示样本集和各故障类别对应的样本数;表示根据轴承故障类别,即健康、内圈故障、外圈故障3类,|Di|表示对应的样本数。
为减少模型的计算量,降低特征参数数据维度,利用主成分分析(PCA)对数据特征参数进行降维处理,消除特征参数之间的相关性。PCA是一种统计学习算法,其主要原理是利用正交变换将线性相关的观测数据转换为少数线性无关的数据,可以在压缩数据的同时有效保留数据之间的不相关性,其表达式为:
TN×r=XN×MPm×r
(4)
式中,T为主成分分析结果;X为观测数据样本矩阵;P为正交矩阵。
2 基于PSO-SVM的故障诊断模型
2.1 支持向量机
支持向量机(SVM)是一种基于统计学习理论的数据挖掘方法,在处理回归问题、模式识别等方面都有广泛的应用[19-21]。其基本原理是通过非线性变换,将低维数据映射到高维空间,以结构风险最小化为目标寻找最大分类边界的超平面。设备故障诊断在本质上属于一个多模式识别或多值分类的问题,因此SVM可以达到较好的故障分类效果。对于给定的样本集,选择合适的核函数和惩罚参数,可以有效的提高故障诊断模型的识别精度。
核函数和惩罚参数C影响SVM分类器的表现性能,常用的核函数有线性核、多项式核、高斯核、拉普拉斯核等[22],其中高斯核函数是最常用的核函数,可将样本映射到更高维的空间内,通过高斯宽度σ确定。惩罚参数C用于调节分类准确度和间接大小的权重,以避免模型出现过拟合,因此,可通过对参数σ和C的寻优来提高SVM分类器的分类精度。
2.2 粒子群优化算法
采用粒子群优化算法(PSO)对SVM分类器参数进行全局寻优,粒子群优化算法又称微粒群算法,是一种通过模拟鸟类觅食过程中的迁徙过程和群聚行为而提出的一种基于群体智能的全局随机搜索算法,该算法根据求解的问题在D维空间中随机生成一个包含N个粒子的粒子群,每个粒子以一定的速度在解空间运动,并向粒子本身最佳位置和种群历史最佳位置靠拢,以实现候选解的变化。粒子i(i=1,2,…,N)位置向量可以表示为xi=(xi1,xi2,…,xiD),速度向量可表示为vi=(vi1,vi2,…,viD),则速度和位置更新公式为:
(5)

2.3 故障诊断模型参数优化
基于PSO-SVM的滚动轴承故障诊断流程如图1所示。
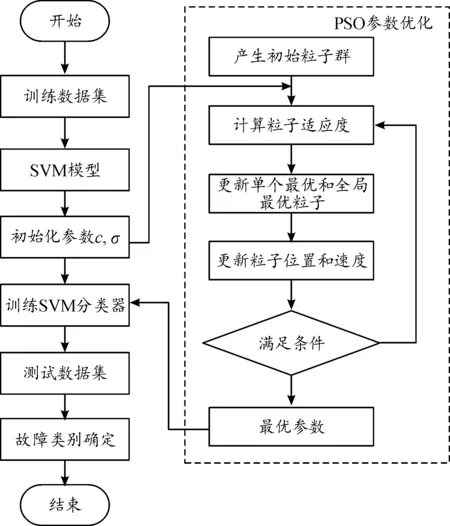
图1 故障诊断流程图
1) 数据预处理。对采集的电流信号与振动信号进行特征提取,按照敏感指标选择对轴承故障类别比较敏感的特征参数,并利用主成分分析对特征参数进行降维并归一化处理。
2) 数据集划分。将归一化处理后的特征参数为模型输入,轴承具体故障为模型输入,随机划分训练数据集和测试数据集,训练数据集和测试数据集的比例为7∶3。
3) SVM分类器模型构建。选择高斯核函数作为SVM分类器的基函数,初始化高斯宽度σ和惩罚参数C。
4) 参数选择与优化。基于训练数据集利用PSO对SVM分类器的参数进行迭代优化,找出SVM分类器的最优参数。
5) 故障类型识别。利用优化后的SVM分类器模型对数据故障类型进行识别,为故障维修和排除提供参考。
3 实例验证
3.1 实验数据集介绍
为验证所提轴承故障诊断方法的有效性,利用德国帕德伯恩大学轴承加速疲劳试验数据集进行案例研究[23]。电流信号和振动信号采样频率64 kHz,工作状态和轴承编号对应故障状态分别如表3、4所示,每组轴承在各工作状态下各采样20个数据段。

表3 轴承工作状态
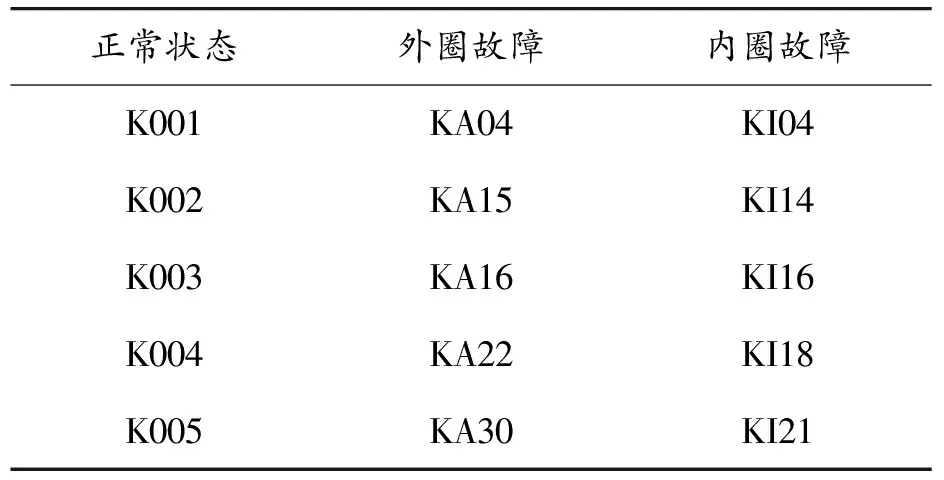
表4 滚动轴承对应故障类型
滚动轴承在不同故障状态下电流信号和振动信号的时域波形分别如图2、3所示,可见难以根据单独的信号特征有效诊断轴承的故障状态。

图2 轴承电流信号时域波形

图3 轴承振动信号时域波形
3.2 混合特征提取
对电流信号和振动信号分别按照表1和表2进行特征提取,并计算各特征参数的信息增益,结果如表5所示。选择阈值大于0.2的特征作为敏感特征,即敏感特征集为[A9,p2,p3,p5,p6,p8,p11,p12,p16,p17,p21,p23,p25,p26]。

表5 各特征信息增益
由于部分特征参数之间存在关联性,导致特征信息存在冗余,增加了模型计算成本。因此,利用PCA算法对特征参数进行降维,根据贡献度将15维特征信息保留至3维。敏感特征集经过PCA降维后3种健康状态的特征数据分布如图4所示,可以看出,每种健康状态的分布点相对集中,可以较好的进行区分识别。

图4 PCA算法降维后状态空间图
3.3 不同特征组合方式对比分析
为了验证选择所选择敏感特征集的有效性,将经过PCA降维的电流信号特征参数、振动信号时域特征参数、振动信号频域特征参数作为特征分类器的输入进行故障诊断,结果如表6所示。
由表6可以看出,利用敏感特征集、电流特征参数、振动信号时域特征参数、振动信号频率特征参数作为PSO-SVM分类器输入时识别准确率分别为98.6%、83.3%、97.5%、95.6%,可以看出在分类模型一致的情况下,以敏感特征集作为模型输入相对单一评价指标具有更高的准确率。

表6 不同特征集诊断准确度
3.4 不同模型结果对比分析
将降维后的特征集作为输入向量进行状态识别,将训练集特征向量输入到PSO-SVM分类器中进行参数寻优和模型训练,然后将测试集数据输入到训练好的分类器模型中进行故障识别,得到的识别结果如图5所示。可以看出,在360个测试样本中仅5个样本被错分,准确率达到了98.6%,证明PSO-SVM分类器在轴承故障诊断方面具有较好的效果。

图5 PSO-SVM识别结果
为了进一步验证PSO-SVM分类器的有效性,使用随机森林、网格搜索支持向量机(GS-SVM)等常用方法进行故障故障模式识别,结果如表7所示。由表7可以看出PSO-SVM、随机森林、GS-SVM的识别准确率分别为98.6%、97.5%和93.1%。在样本数据一致和数量相同的条件下PSO-SVM分类器相对随机森林、网格搜索支持向量机分类方法具有更高的准确率,说明PSO-SVM能够更有效的区分滚动轴承的故障类型。

表7 不同故障诊断方法的准确率
4 结论
针对旋转部件故障诊断,综合考虑电流信号特征和振动信号特征提出了混合特征与PSO-SVM的旋转部件故障诊断方法,利用德国帕德伯恩大学轴承加速疲劳试验数据集进行验证。通过对比以不同特征提取方式作为特征输入对故障诊断模型识别精度的影响,证实了以混合特征参数作为模型输入可以提高诊断模型的识别精度。通过与常用的故障模型进行对比,证实了识别精度高于其他常见的故障诊断模型。说明基于混合特征的PSO-SVM故障诊断方法具有较高的故障识别准确率,可用于各类轴承的故障诊断中,具有一定的现实意义。
