甘油连续生物歧化过程的状态反馈最优控制
2022-10-11徐恭贤王雨竹李竹茜
徐恭贤,王雨竹,李竹茜
(渤海大学 数学科学学院, 辽宁 锦州 121013)
0 引言
1,3-丙二醇在化工、食品、化妆品和制药等行业中具有广泛的应用[1-3]。目前,国内外研究人员主要以罗伊氏乳杆菌、克雷伯氏杆菌、脱氮假单胞菌、丁酸梭菌等歧化甘油的微生物发酵法来生产1,3-丙二醇。Menzel等[4]指出,克雷伯氏杆菌歧化甘油生产1,3-丙二醇过程中存在着明显的振荡、抑制等非线性现象。Zeng等[5],修志龙等[6]和Sun等[7]先后应用过量动力学模型描述了甘油生物歧化过程中的过量代谢特性、多态现象以及酶催化与基因调控动力学。通过应用代谢工程原理与方法,文献[8-11]提高了产物1,3-丙二醇的生产强度。针对生物系统存在的参数与模型不确定性问题,徐恭贤等[12]和Zhu等[13]分别应用H∞与μ分析方法,研究了甘油连续微生物发酵系统的鲁棒控制,取得了较好的控制效果。Xu等[14]和Paranhos等[15]给出了甘油生物歧化过程过量动力学系统、酶催化系统以及基因调控系统的非线性优化模型与求解算法,取得了良好的应用效果。为了推断克雷伯氏杆菌歧化甘油过程的代谢目标,徐恭贤等[16]和Xu等[17]提出了多层规划模型,并给出了有效的求解算法。应用表明,该类方法可以获得更好的计算结果。Yuan等[18]研究了甘油生物歧化系统的最优控制问题,但该项研究工作没有给出控制变量与系统状态(或输出)变量之间的闭环关系,因此最优控制属于开环控制。贝泓涵等[19]研究了微生物连续发酵生产1,3-丙二醇过程的线性反馈最优控制,但其给出的方法与计算结果存在如下问题:① 未能给出高质量的最优解,主要体现在目的产物1,3-丙二醇的浓度最优值较低,见本文结果分析与比较部分的表3;② 设计的反馈控制不在约束范围内,见文献[19]的图1,原因是在寻找最优反馈控制参数时没有考虑控制变量的有界性。因此有必要给出新的反馈控制模型与方法。基于以上分析,提出适于甘油连续生物歧化过程的状态反馈最优控制模型及其有效求解算法,取得了较好的应用效果。
1 甘油连续生物歧化过程的数学描述
基于文献[20],应用如下非线性常微分方程系统描述甘油连续生物歧化过程:

(1)
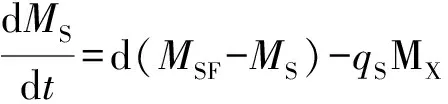
(2)

(3)
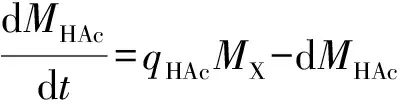
(4)
(5)
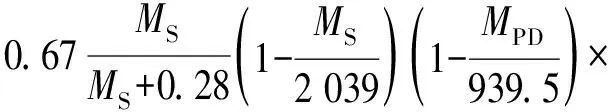
(6)
(7)
(8)
(9)
(10)
t∈[0,T]
(11)
MX(0)=MX0
(12)
MS(0)=MS0
(13)
MPD(0)=MPD0
(14)
MHAc(0)=MHAc0
(15)
MEtOH(0)=MEtOH0
(16)
式(1)—(16)中:MSF为进料甘油的浓度,mmol·L-1;d为稀释速率,h-1;MX为生物量,g·L-1;MS为反应器中甘油的浓度,mmol·L-1;MPD为产物1,3-丙二醇的浓度,mmol·L-1;MHAc为产物乙酸的浓度,mmol·L-1;MEtOH为产物乙醇的浓度,mmol·L-1;MX0、MS0、MPD0、MHAc0和MEtOH0为初始浓度;t为时间,h;T为终端时刻,h;μX为比生长速率,h-1;qS为比消耗速率,mmol·g-1·h-1;qPD、qHAc和qEtOH为产物的比生成速率,mmol·g-1·h-1。
2 最优控制模型
针对甘油连续生物歧化的非线性常微分方程系统(1)—(16),以最大化终端时刻t=T时目的产物1,3-丙二醇浓度MPD(T)为优化性能指标,以稀释速率d和进料甘油浓度MSF为控制变量,提出了如式(17)—(35)所示的最优控制模型。其中,式(29)—(33)是MX、MS、MPD、MHAc和MEtOH的取值范围;式(34)—(35)是控制变量d和MSF的取值范围,式(34)的引入是为了防止反应过程发生“洗出”现象。
maxMPD(T)
(17)
(18)

(19)
(20)
(21)
(22)
t∈[0,T]
(23)
MX(0)=MX0
(24)
MS(0)=MS0
(25)
MPD(0)=MPD0
(26)
MHAc(0)=MHAc0
(27)
MEtOH(0)=MEtOH0
(28)
0.001≤MX≤10
(29)
0≤MS≤2 039
(30)
0≤MPD≤939.5
(31)
0≤MHAc≤1 026
(32)
0≤MEtOH≤360.9
(33)
0.05≤d≤0.5
(34)
100≤MSF≤2 039
(35)
3 状态反馈最优控制
在甘油连续生物歧化过程的非线性常微分方程系统(1)—(16)中,影响目的产物1,3-丙二醇形成的主要因素有2个,1个是控制变量稀释速率d和进料甘油浓度MSF,另1个是生物量MX和反应器中甘油浓度MS。因此,设计如下状态反馈控制:
(36)
式(36)中,K∈R2×2为反馈增益矩阵,可表示为
其中,反馈参数k11、k12、k21和k22的取值范围为
将式(36)代入式(17)—(35)中得动态优化问题(记为DOP1):
maxMPD(T)
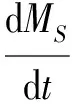
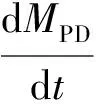
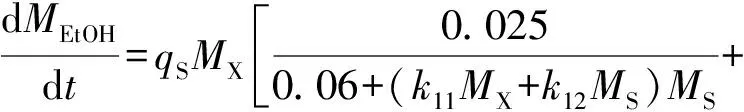
(k11MX+k12MS)MEtOH
式(23)—(33)中:
0.05≤k11MX+k12MS≤0.5
100≤k21MX+k22MS≤2039
4 求解方法
为叙述方便,设
x=(x1,x2,x3,x4,x5)T=
(MX,MS,MPD,MHAc,MEtOH)T
y=(y1,y2,y3,y4)T=
(k11,k12,k21,k22)T
f(x(T),y,T)=x3(T)
g1(x,y)=μXMX-(k11MX+k12MS)MX
g2(x,y)=(k11MX+k12MS)·
(k21MX+k22MS-MS)-qSMX
g3(x,y)=qPDMX-(k11MX+k12MS)MPD
g4(x,y)=qHAcMX-(k11MX+k12MS)MHAc
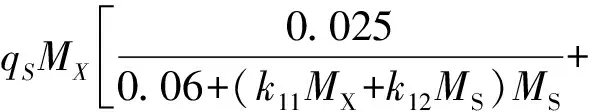
(k11MX+k12MS)MEtOH
g(x,y)=(g1(x,y),g2(x,y),g3(x,y),
g4(x,y),g5(x,y))T
p1(x,y)=y1x1+y2x2
p2(x,y)=y3x1+y4x2
x0=(MX0,MS0,MPD0,MHAc0,MEtOH0)T
则动态优化问题DOP1可表示为如下形式(记为DOP2):
maxf(x(T),y,T)=x3(T)

x(0)=x0
x≤(10,2 039,939.5,1 026,360.9)T
x≥(0.001,0,0,0,0)T
0.05≤p1(x,y)≤0.5
100≤p2(x,y)≤2 039
yl≤y≤yu
t∈[0,T]
由于问题DOP2中含有复杂的状态方程dx/dt=g(x,y),故基于有限元配置形式先将其离散化。
将[0,T]划分为m个有限元
[ηi,ηi+1],i=1,2,…,m
其中,0=η1<η2<…<ηm<ηm+1=T。则dx/dt=g(x,y)在有限元[ηi,ηi+1]上的解可近似表示为
其中:xLx(t)为拉格朗日多项式,xLx(tij)=xij;Lx表示[ηi,ηi+1]上状态变量x(t)的配置点个数。将xLx(t)代入dx/dt=g(x,y)中,可得
(37)
令tik=ηi+Δηiδk,Δηi=ηi-ηi+1,δk∈[0,1],则式(37)可进一步化为
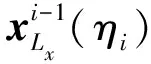
根据以上推导与分析,将动态优化问题DOP2转化为如下非线性规划问题(记为NLP1):
maxf(x(T),y,T)=x3(T)

i=1,2,…,m;k=1,2,…,Lx
x10=x0
xLx(tij)≤(10,2 039,939.5,1 026,360.9)T
i=1,2,…,m;j=0,1,…,Lx
xLx(tij)≥(0.001,0,0,0,0)T
i=1,2,…,m;j=0,1,…,Lx
0.05≤p1(tij,xij,y)≤0.5
100≤p2(tij,xij,y)≤2 039
yl≤y≤yu
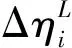
非线性规划问题NLP1是一个具有多变量和约束条件的大规模优化问题,为了有效求最优解,提出如下算法对其进行求解。
算法1:
步骤1给定计算次数n。令迭代次数w=1;
步骤2在第w(w≥1)次迭代,随机产生初始可行点,应用内点法求解非线性规划问题NLP1,令最优解为u(w),目标值为f(w);
步骤3若w=n,则停止迭代,转步骤4;否则令w=w+1,转步骤2;

采用多初始点策略可以有效解决内点法初始点难以确定的问题,改善内点法的求解效率。
5 结果与比较
在甘油连续生物歧化过程的状态反馈控制中,各物质的初始浓度分别取为MX0=0.1 g·L-1,MS0=400 mmol·L-1,MPD0=0 mmol·L-1,MHAc0=0 mmol·L-1和MEtOH0=0 mmol·L-1;终端时刻取为T=100 h;反馈控制参数的取值范围取为
0≤k11≤1 000
0≤k12≤1 000
0≤k21≤1 000
0≤k22≤1 000
通过算法1可得目的产物1,3-丙二醇浓度的最优值为MPD(T)=546.121 499 mmol·L-1,相应的最优反馈控制参数如表1所示。表2给出了终端时刻T=100 h时各控制变量以及各物质浓度的最优值。

表1 最优反馈控制参数

表2 T=100 h时变量的最优值
表3为本文算法与文献[19]方法的计算结果比较,其中各物质的初始浓度分别取为MX0=0.1 g·L-1,MS0=400 mmol·L-1,MPD0=0 mmol·L-1,MHAc0=0 mmol·L-1和MEtOH0=0 mmol·L-1;终端时刻取为T=100 h。可见,本文获得的目的产物1,3-丙二醇的浓度为546.121 499 mmol·L-1,是文献[19]方法结果的1.279 463倍,说明本文方法具有更好的寻优性能。

表3 本文方法与文献[19]方法的计算结果
在状态反馈控制器的作用下,各控制变量以及各物质浓度随时间的变化曲线如图1—7所示,从图中可以看出,各变量均在给定的约束范围内。
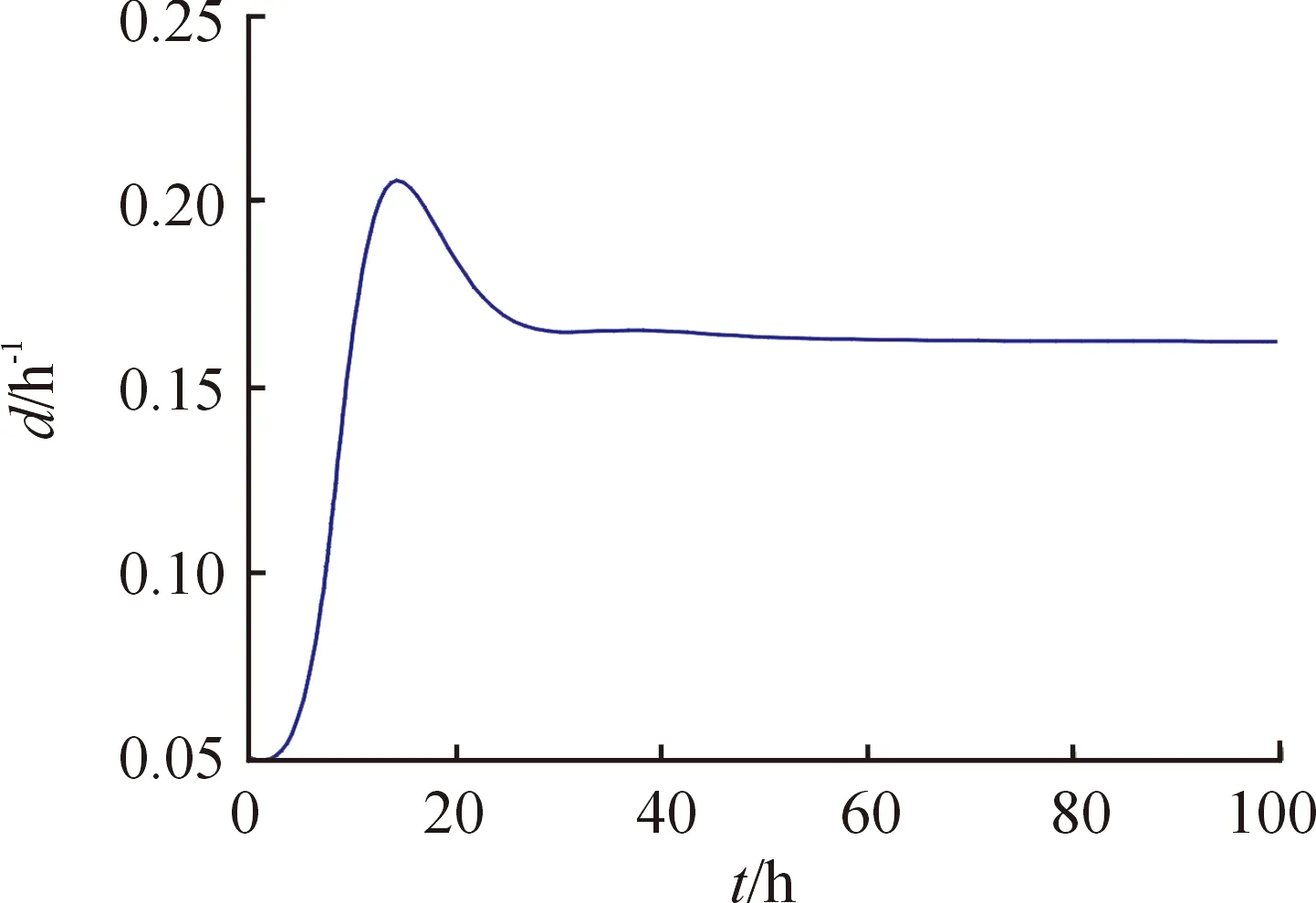
图1 控制变量(稀释速率d)曲线

图2 控制变量(进料浓度MSF)曲线

图3 生物量(MX)曲线

图4 甘油浓度(MS)曲线

图5 1,3-丙二醇浓度(MPD)曲线
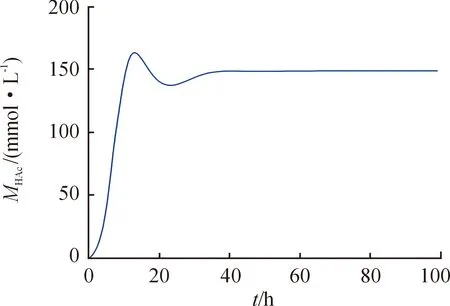
图6 乙酸浓度(MHAc)曲线

图7 乙醇浓度(MEtOH)曲线
6 结论
研究了甘油连续生物歧化过程的状态反馈最优控制。以最大化终端时刻目的产物1,3-丙二醇浓度为优化性能指标,提出了最优控制模型。通过设计线性部分状态反馈控制器,将最优控制模型转化为含反馈控制参数的动态优化问题,并提出有效算法对其进行求解,实现了甘油连续生物歧化过程的状态反馈最优控制。本文算法获得的产物1,3-丙二醇浓度的最优值为546.121 499 mmol·L-1,是已有方法结果的1.279 463倍,说明本文方法具有更好的寻优性能。
