一个代数不等式的证明及变式

湖南省桃江县第一中学 (413400) 胡芳举 徐令芝

笔者在给学生讲解“蒙日圆”时得到了如下一个有趣的不等式：已知x12+y12=x22+y22= 1，且mx2+ny2≥m+n(m,n>0)，求证m(x-x1)(x-x2)+n(y-y1)(y-y2)≥0.

这个不等式对称优美，但变量较多，证明比较棘手，本文将给出这个不等式的两个证明及两个变式.

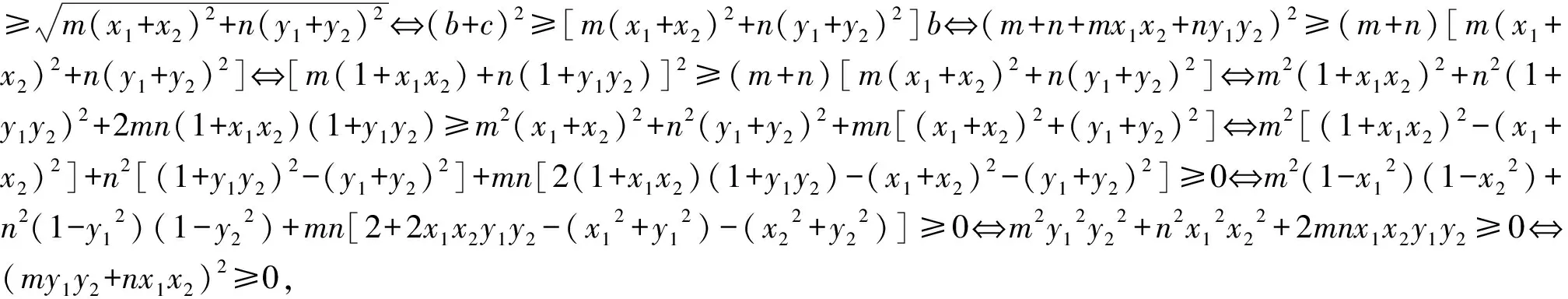
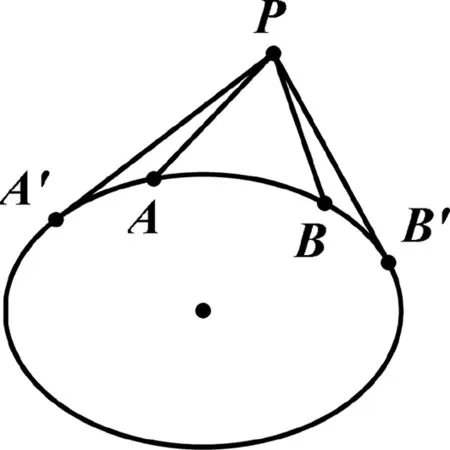
图1

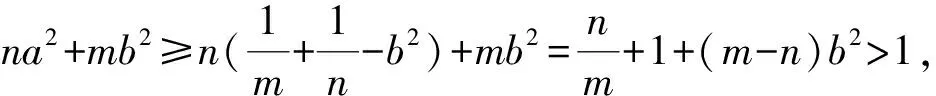
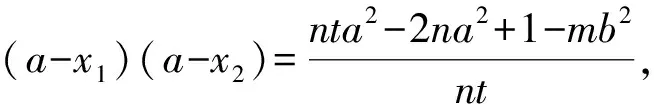
最后给出两个变式：

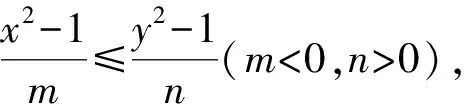
变式2 已知变量x,y,α,β满足m(x-cosα)·(x-cosβ)+n(y-sinα)(y-sinβ)≤0(m,n为正常数)，求mx2+ny2的最大值.

注：mx2+ny2的最大值为m+n.