动中探定 以定制动——一道2022年福建省高三质检题的探究

福建省仙游第一中学 (351100) 林碧霞福建教育学院数学教育研究所 (351100) 蔡海涛

1 试题呈现

(2022年福建省高三诊断性测试第11题)正方体ABCD-A1B1C1D1中，M，N，P分别为棱AB，CC1，C1D1的中点，Q∈平面MNP,B1Q=AB，直线B1Q和直线MN所成角为θ，则( ).

C.A,M,N,P四点共面 D.PQ∥平面ACD1

2 试题分析

本题以正方体为载体，考查空间中直线与直线、直线与平面的位置关系，线线所成的角、动点的轨迹问题等基础知识；考查推理论证和空间想象等能力；考查逻辑推理、直观想象和数学运算等核心素养.对于选项B，涉及立体几何的中的动态问题，因为图形的“不确定性”导致学生解题障碍.

3 多解探究

本题答案BD，选项A，C，D容易分析，限于篇幅本文仅对选项B进行分析.

解法1：(向量法)过M，N，P做正方体ABCD-A1B1C1D1的截面，易得为正六边形，设与线段AA1的交点为E，连接B1D，连接B1M，B1N,DN,DM，易得B1D⊥面PMN.设B1D交平面PMN于O点.

图1

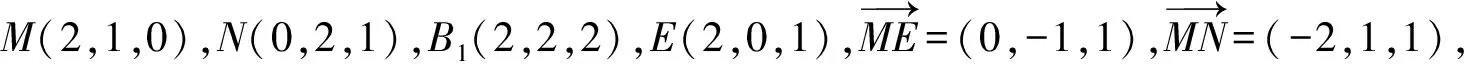
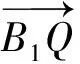
4 方法归纳

立体几何的动态问题是高考的热点，常见的立体动态问题有动点的变化和截面问题，还有平面图形的翻折、几何体的平移和旋转以及投影等.该类问题中的“不确定性”元素往往成为学生思考与求解的思维障碍.这类问题求解的关键是根据题意认真分析“动”的元素的变化特点，寻找在变化过程中蕴含的静态因素，再从静态因素中，找到解决问题的突破口.本题探寻变化过程中的不变关系，用向量法定平面，用轨迹法确定动点轨迹，这两种方法都是解决立体几何有关角度问题的常用策略.