切线法“三用”证明一类不等式
2022-10-10湖北省荆州市监利市职教中心433300
湖北省荆州市监利市职教中心 (433300) 张 琴
导数进入高中数学教材,为我们研究函数的性质——单调性,极值与最值增加了强有力的工具,为高中数学解题注入了新的活力.在各层次的数学测试与竞赛中,常有一些整式、分式、无理不等式的证明,这些不等式的结构对称、形式优美,其证法构思精巧,异彩纷呈,让人观而叹止.其实,不等式的证明可以看作是函数载体下的最值或极值问题,因此,导数为我们研究不等式的证明提供了一种新途径和方法——以直代曲,即利用函数图象在某点处的切线来逼近曲线,以证明一类对称和不等式.
1.切线法的解释
对于定义在区间D上的可导函数y=f(x),若记y=f(x)的图像在x0(非拐点)处的切线方程为y=g(x),且在区间(x0-δ,x0+δ)⊆D内,恒有f(x)≤g(x)(或f(x)≥g(x)),则在区间(x0-δ,x0+δ)内,用直线y=g(x)替代曲线y=f(x)对不等式进行放缩,虽然这种替代是近似的,但它的优点在于,将复杂的运算变形化成一次整式计算,避免高超的变形运算.下面举例说明切线法的应用.
2.观其形,直接应用切线法
若所需证明的不等式为多变量的对称和形式,即,若∑x=A,则∑f(x)≥C(或≤C)(其中A,C为常数,Σ表示循环求和),则可研究函数y=f(x)与其在等号成立的点处的切线方程y=g(x)的之间所具备的不等关系进行放缩,直接应用切线逼近曲线,达到证明命题之目的.
例1 若实数a,b,c>0,且a+b+c=1,则


评注:直接利用切线方程证明不等式,看似计算繁琐,特别是证明f(x)-g(x)≥0(或≤0)时需要进行因式分解,但由于我们已经确定等号成立的平衡点x0,因此,只需利用多项式除法,用x-x0除f(x)-g(x)即可将其分解完全.
3.辨其式,变形应用切线法
如果所证不等式为关于变量的轮换对称式,但条件(或结论)不符合切线法使用之结构,可以考虑变化条件(或结论),再证明之.
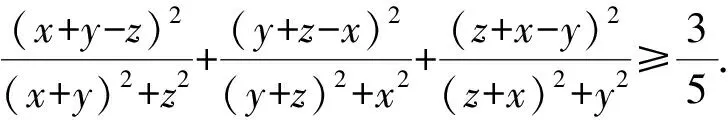


评注:对于齐次不等式,我们可以通过有效增设∑x=1,使之满足切线法使用条件.另外,利用切线法证明不等式,要求所证不等式的一边为和式且每一项只含有一个变量.若不等式不符合要求,可对不等式适当变形,以实现之.

分析:此不等式虽然是关于a,b,c的对称式,但不等式的左端貌似不是∑f(x)的形式,因此利用均值不等式将和a+b转化为积ab,使待证不等式得到加强,并变形为对称和形式.
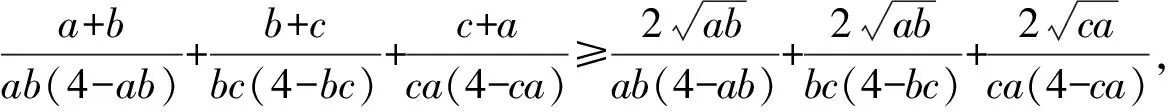


分析一:考虑到待证不等式的形式为∑f(x)≥C,但题设中的变量的关系为平方和,不符合∑x=A,故对条件作适当换元,替换为一次变量的和后,再用切线法证明.
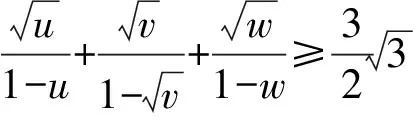
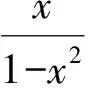

有时,在约束条件下,所研究的曲线与切线所对应的函数的大小关系并不恒成立,则需要我们对关系成立与不成立的变量区间分而治之,各个击破,对两类区间内的不等关系分类讨论.
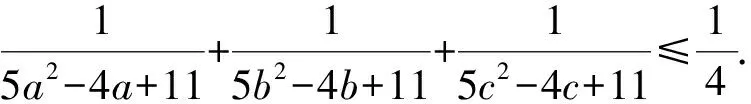

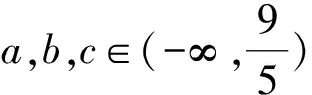



4.品其意,升维应用切线法
对于形如∑x=A,则∑f(x,y,z)≥C(或≤C)(其中A,C为常数,∑f(x,y,z)为x,y,z的轮换对称式),若将f(x,y,z)难以放缩为单变量函数式,可将函数f(x,y,z)看作曲面f(x,y,z)=0,利用偏导求出约束条件∑x=A下的平衡点(x0,y0,z0)处的切平面g(x,y,z)=0,利用切平面逼近曲面,再验证f(x,y,z)与g(x,y,z)之间的大小关系,从而证明命题.下面升维再证明例3.

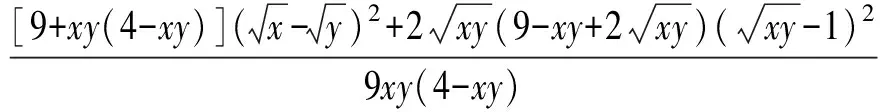


从上面例题,可以看出,切线法为我们提供了证明一类和式不等式的新方法,其证题思路清晰,易于操作,可以避开让人叹止的高超构造、拆分组合与鬼斧神工的变形技巧;但我们也应注意,运用切线法解题时,应确保原不等式中等号成立的条件一致.
