混合型CMOS-忆阻异或逻辑单元设计及其应用
2022-10-10王旭亮陈俊杰罗文瑶吕伟锋
王旭亮,林 弥,陈俊杰,韩 琪,罗文瑶,吕伟锋
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
0 引 言
1971年,蔡少棠教授首次提出忆阻器的概念,是继电阻、电容和电感之后的第4种基本电路元件[1]。1976年,蔡少棠教授进一步分析了忆阻器的基本特征,提出忆阻系统[2]。忆阻器概念自提出后,相关研究仅停留在理论层面。2008年,惠普实验室对忆阻器进行物理实现,证实了忆阻器的存在[3]。随后,忆阻器在非易失性存储器[4-5]、人工神经网络[6-8]、混沌系统[9]和数字逻辑电路[10-11]等领域取得了重大成果。目前,忆阻器和CMOS晶体管构成的混合型电路是数字逻辑电路研究的主要方向之一,如基础逻辑门单元[12-14]、全加器、乘法器[15-19]以及复杂的逻辑电路等。文献[12]设计的忆阻比例“或”门和“与”门分别由2个极性相反的忆阻器串联组成,并使用CMOS反相器来提供完整的逻辑门,实现了半加及全加电路;文献[14]设计了一种忆阻器与CMOS晶体管结合的新结构多功能逻辑门,同时实现了“与”门、“或”门和“异或”门功能,并设计了基于多功能逻辑门的超前进位加法器;文献[17]设计了由1个忆阻器和1个NMOS管构建的“非”门逻辑电路,并基于“非”门电路设计了2个输入“或非”门和N个输入“或非”门,构建了一种由1个NMOS管和5个忆阻器构成的同时具有“异或”和“与”逻辑功能的模块,使用多功能模块设计了两位二进制乘法器,改善了芯片使用面积和延迟等问题。
异或运算作为基本的布尔逻辑,可以构成完备集,是全加器、乘法器、计数器等各种逻辑单元的关键组成部分,功能十分强大,但单一的逻辑功能影响了电路的集成化设计。本文以忆阻器和CMOS为核心,设计了一款全新的忆阻异或逻辑电路,并在此基础上,搭建了仅由异或逻辑单元构成的混合型CMOS-忆阻全加器电路,实现了全加器功能。
1 Biolek阈值型忆阻器模型
由于忆阻器的制备较为困难,可采用忆阻器等效模型进行设计和研究。目前,较为热门的等效模型有边界偏移模型[3]、双极性阈值行为模型[20]等。其中,Biolek阈值型忆阻器模型[21]具有确定的阈值电压以及较大差的高低阻态,更适合数字逻辑电路,因此,本文使用Biolek阈值型忆阻器模型进行电路设计,忆阻器电路符号如图1(a)所示。Biolek阈值型忆阻器模型的数学表达式如下:
I=X-1VM
(1)
(2)
f(VM)=β(VM-0.5)[|VM-Vt|-|VM+Vt|]
(3)
W(X,VM)=θ(VM)θ(ROFF-X)+θ(-VM)θ(X-RON)
(4)
式中,VM为忆阻器两端电压,I为流经忆阻器的电流,Vt为阈值电压,X为忆阻器阻值,ROFF和RON分别为忆阻器的高阻态阻值和低阻态阻值,β为忆阻变化率,θ为阶跃函数,W(X,VM)为阶跃函数构成的窗函数。Biolek阈值型忆阻器模型具有可设置的开关电阻比和阈值电压,在一定的操作电压下可实现高低阻态的可逆转变。取β=1013,Vt=4 V,ROFF=100 kΩ,RON=100 Ω,在模型两端施加频率为1 kHz,幅值为6 V的正弦信号,得到伏安特性曲线如图1(b)所示。
由图1(b)可知,当加载在阈值型忆阻器两端的信号电压超过其阈值电压时,忆阻器的阻值在ROFF和RON之间转换,由于ROFF和RON的数值相差较大,故曲线具有明显的开关效应,适用数字逻辑电路的设计。
2 混合型CMOS-忆阻异或逻辑单元的设计
本文运用Biolek阈值型忆阻器和CMOS晶体管设计的忆阻异或逻辑单元如图2所示,由5个CMOS晶体管和1个忆阻器Ma组成,其中M1,M2,M3为NMOS晶体管;M4,M5为PMOS晶体管;Vcc为工作电源,VA和VB为输入电压,Vout为输出电压。忆阻器参数设定为β=1013,Vt=4 V,ROFF=100 kΩ,RON=100 Ω,NMOS和PMOS晶体管沟道宽长比均为100,M1,M2,M3的型号为M2N6802,阈值电压为3.5 V,M4,M5的型号为M2N6849,阈值电压为-3.5 V。本文设计的电路结构中,忆阻器和CMOS晶体管均采用以上参数。
假设阈值型忆阻器初态为低阻态,输入信号的高电平为逻辑1,低电平为逻辑0,其电路工作过程如下:
(1)当输入信号A为低电平时,M1,M2截止,M4导通。若输入信号B为低电平,忆阻器Ma两端无电压差,保持低阻态,忆阻值RMa=RON,则输出支路电压均为低电平,Vout为低电平;若输入信号B为高电平,忆阻器正向偏置,忆阻值RMa=ROFF,输出支路电压均为高电平,Vout为高电平。
(2)当输入信号A为高电平时,M1,M2导通,M4截止。若输入信号B为低电平,M5导通,电源信号Vcc由M5和M1传输至M4的漏极,忆阻器Ma两端无电压差,保持低阻态,忆阻值RMa=RON,等效为小电阻接入到Vcc和地信号中,则Vout为高电平;若输入信号B为高电平,忆阻器正向偏置,忆阻值RMa=ROFF,M3导通,接地信号由M3和M1传输至M4的漏极,忆阻器等效为大电阻,输出信号相当于接地,则Vout为低电平。
综上分析可知,当输入信号A和B相同时,Vout为低电平;当A和B不相同时,Vout为高电平。所以,图2电路实现了异或逻辑功能。
取时域仿真周期为4 ms,步长为10 μs,Vcc为5 V,VA和VB均为5 V的输入信号电压值,混合型CMOS-忆阻异或逻辑单元的PSPICE仿真结果如图3所示,输出电压的高电平为4.7~5.0 V,低电平为0 V。
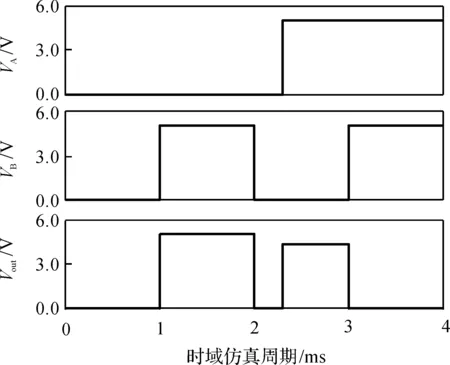
图3 混合型CMOS-忆阻异或逻辑单元仿真曲线
从图3可以看出,本文设计的CMOS-忆阻异或逻辑单元实现了正确的逻辑功能。
3 混合型CMOS-忆阻异或逻辑单元的应用
3.1 全加器理论
2个多位二进制数相加时,除了最低位外,每一位都应该考虑来自低位的进位,即将2个对应位的加数和来自低位的进位相加,进而实现全加器运算。假设A是加数,B是被加数,Cin是来自低位的进位,S是本位和,Cout是向高位的进位,全加器的数学表达式如下[22]:
S=A⊕B⊕Cin
(5)
Cout=AB+Cin(A⊕B)
(6)
式(5)和式(6)都用到异或运算,为了提高单一逻辑门的利用率,将表达式主体重组为异或逻辑,对式(6)中的AB进行变换,得到:
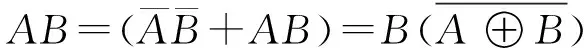
(7)
式(6)可表示为:
(8)
由式(8)可知,进位输出信号Cout的表达式中存在异或逻辑和同或逻辑,若把异或运算(A⊕B)作为控制信号,进位输出Cout可看作是1个2选1的数据选择器,当(A⊕B)为低电平时,输出B;当(A⊕B)为高电平时,输出Cin。所以,在图2的基础上,只需增加1个数据选择器单元即可实现忆阻器全加器的功能。
3.2 混合型CMOS-忆阻数据选择器
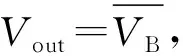
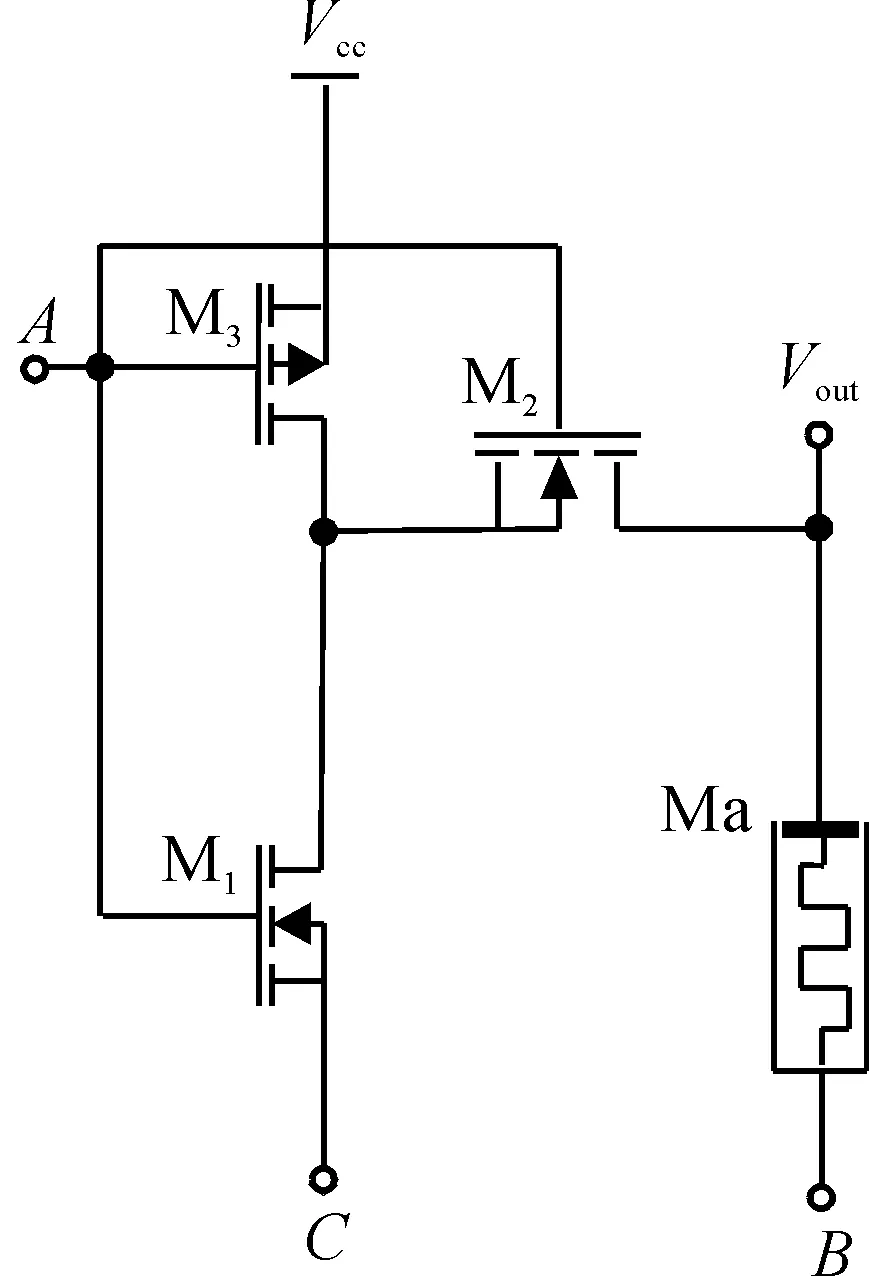
图4 混合型CMOS-忆阻2选数据选择器电路图
假设阈值型忆阻器初态为低阻态,其电路工作过程和第2节异或电路类似,即当VA为低电平时,Vout=VB;当VA为高电平时,Vout=VC。实现了2选1选择器的功能。
时域仿真周期为4 ms,步长为10 μs,Vcc为5 V直流电源,VA和VB均为5 V的输入信号电压值CMOS-忆阻2选1数据选择器电路的PSPICE仿真结果如图5所示,输出电压的高电平为4.6~5.0 V,低电平为0 V。
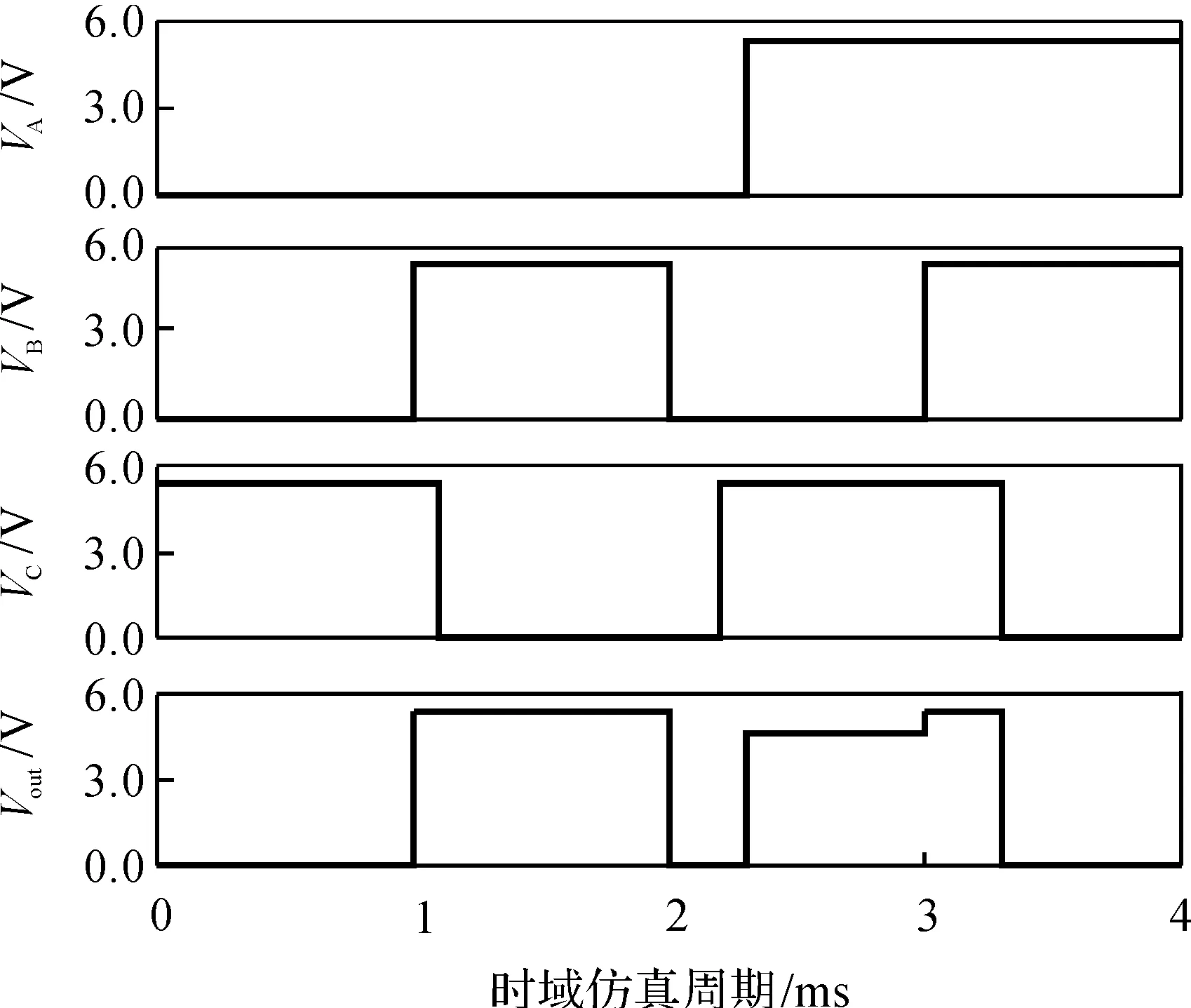
图5 混合型CMOS-忆阻2选1数据选择器仿真曲线
由图5可以看出,当输入信号电压值VA为低电平时,Vout=VB;当VA为高电平时,Vout=VC,说明混合型CMOS-忆阻2选1数据选择器实现了2选1选择器功能。
3.3 混合型CMOS-忆阻全加器
根据式(5)和式(8),在CMOS-忆阻异或逻辑单元和CMOS-忆阻2选1数据选择器电路的基础上,本文设计了混合型CMOS-忆阻全加器,其电路如图6所示,由3个阈值型忆阻器和13个MOS管构成。图6中,A,B,Cin表示输入信号,Cout表示进位输出信号,S表示和输出信号,Q为电路中间信号,表示A与B的异或运算的输出信号。

图6 混合型CMOS-忆阻全加器电路图
时域仿真周期为4 ms,步长为10 μs,Vcc为5 V直流电源,VA和VB均为5 V的输入信号电压值,CMOS-忆阻全加器电路的PSPICE仿真结果如图7所示,输出电压的高电平为4.6~5.0 V,低电平为0 V。

图7 混合型CMOS-忆阻全加器仿真曲线
由图7可以看出,混合型CMOS-忆阻全加器电路具有正确的全加器逻辑功能。
由于忆阻器具有纳米尺寸,运行速度是CMOS的104倍[23],其制作工艺可在CMOS的金属层完成,所以,相较于传统CMOS晶体管,使用忆阻器和CMOS混合搭建的数字电路的逻辑电路芯片的占用面积更小,电路功耗更低。在同种材料下,器件的数量是影响芯片的占用面积的主要因素,本文选取文献[14]、文献[18]及本文这3种不同的混合型CMOS-忆阻全加器电路,从忆阻器和CMOS晶体管的使用数量上进行比较,结果如表1所示。

表1 不同设计方法下忆阻全加器的元器件数量
从表1可以看到,与文献[14]、文献[18]设计的忆阻全加器电路相比,本文设计的混合型CMOS-忆阻全加器的晶体管和忆阻器均有一定数量的减少,说明本文设计的混合型CMOS-忆阻全加器占用面积更小,功耗更少。
4 结束语
本文运用CMOS和忆阻器,设计了一款可进行逻辑转换的混合型CMOS-忆阻异或逻辑单元,实现了异或和选择器的逻辑功能,设计电路使用的器件数量少,结构简单,功耗小。同时,本文还基于设计的异或单元搭建了混合型CMOS-忆阻全加器电路,相比于现有的忆阻器全加器应用的器件数量更少,结构更加简单。后期将利用该设计方法继续搭建乘法器等复杂逻辑电路。
