基于Coons曲面的插值细分方法

范 健，李亚娟，刘建贞，邓重阳

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

与参数曲面相比，细分曲面更易表达复杂拓扑结构和几何特征，计算效率更高，发展及应用更广泛[1]。现有的细分曲面造型方法分为插值型细分方法[2]和逼近型细分方法[3]两大类。对插值型细分方法而言，通常从点的位置信息出发，经过网格不断细化从而得到其极限曲面；而极限曲面不易像参数曲面一样得到相应的几何信息，且在不改变初始网格点位置的前提下，不方便调整极限曲面的局部形状。Coons曲面[4]是根据边界条件而成的曲面，是最常见的参数曲面之一，与Bézier曲面和B样条曲面相比，其优点在于插值给定边界条件。本文提出一种基于Coons曲面的插值细分方法，适用于任意拓扑四边形网格。满足点插值的同时也满足切向插值，容易得到曲面的导矢信息，且在不改变初始网格点位置的情况下，可通过改变初始切向达到调整极限曲面形状的效果。

1 预备知识

1.1 Coons曲面

给定参数曲面Z(u,v)，0≤u,v≤1，它在u方向和v方向的一对边界分别记为Z(u,0)，Z(u,1)，Z(0,v)，Z(1,v)。若对其边界作插值，得到新的曲面为：

X(u,v)=(1-u)Z(0,v)+uZ(1,v)+(1-v)Z(u,0)+vZ(u,1)-

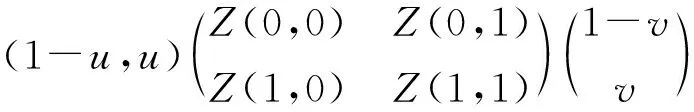
(1)

称曲面X(u,v)为Coons曲面，其中Z(0,0)，Z(0,1)，Z(1,0)，Z(1,1)为参数曲面Z(u,v)的4个角点。显然，参数曲面Z(u,v)的边界线也是Coons曲面X(u,v)的边界线。

通过式(1)得到Coons曲面两方向u，v的切向为：

Xu(u,v)=(1-v)Zu(u,0)+vZu(u,1)-Z(0,v)+Z(1,v)-

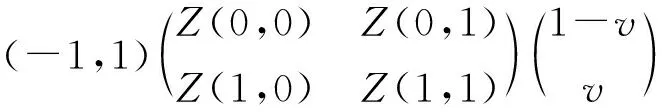
(2)

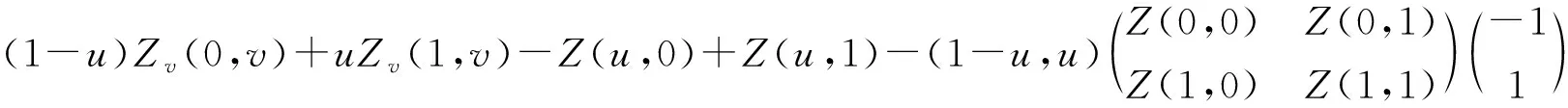
(3)

式中，Zu(u,0)，Zu(u,1)，Zv(0,v)和Zv(1,v)分别为边界曲线Z(u,0)，Z(u,1)，Z(0,v)和Z(1,v)的切向。

1.2 拓扑规则

本文研究四边形网格的插值型细分方法，面的分裂方式是1分为4，分裂方式如图1所示。对于给定的四边形网格，细分过程中，每个面和每条边分别插入1个新点，称之为新面点和新边点，每条边的新边点分别与边的两端点连接，每个面的新面点分别与4条边的新边点连接，形成新的细分网格。

图1 面的分裂方式

2 基于Coons曲面的插值细分方法

对于面1-4分裂的带切向的插值细分方法，每次细分过程中，应分别计算每条边的新边点及其切向和每个面的新面点及其切向。

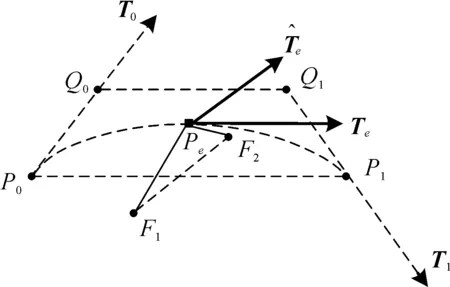
图2 新边点的计算示图

2.1 新边点及其切向的计算

为了叙述方便，分别称新边点的两方向切向为沿边切向和跨界切向，沿边切向是新边点对应于新边点和旧边的端点所连边的切向，跨界切向是新边点对应于新边点和新面点所连边的切向。新面点的计算如图2所示，令旧边e的2个端点分别为P0和P1，向量T0和T1分别为点P0和P1的沿边e的切向，l为边e的长度，辅助点Q0和Q1分别为：

P0，Q0，Q1和P1依次相连形成特征多边形，由此构造1条三次Bézier曲线[5]：

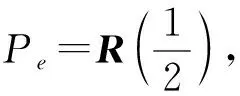
令包含内部边e的2个面的新面点分别为F1和F2。对于任何一个满足一定连续性的细分方法，只要细分次数足够多，新边点和临近两新面点定是近乎共线，因此，新边点Pe的跨界切向为：

2.2 新面点及其切向的计算

新面点的计算如图3所示，面f的4条边对应的三次Bézier曲线分别为Z(u,0)，Z(u,1)，Z(0,v)，Z(1,v)，以它们作为边界曲线，构造1个插值这些曲线的Coons曲面X(u,v)。根据式(1)—式(3)，取Coons曲面内部一点，

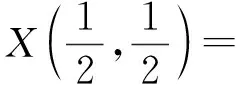
和该点处的两方向切向，

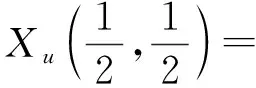
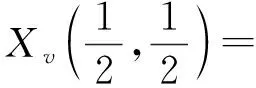
作为面f的新面点与其两方向切向。

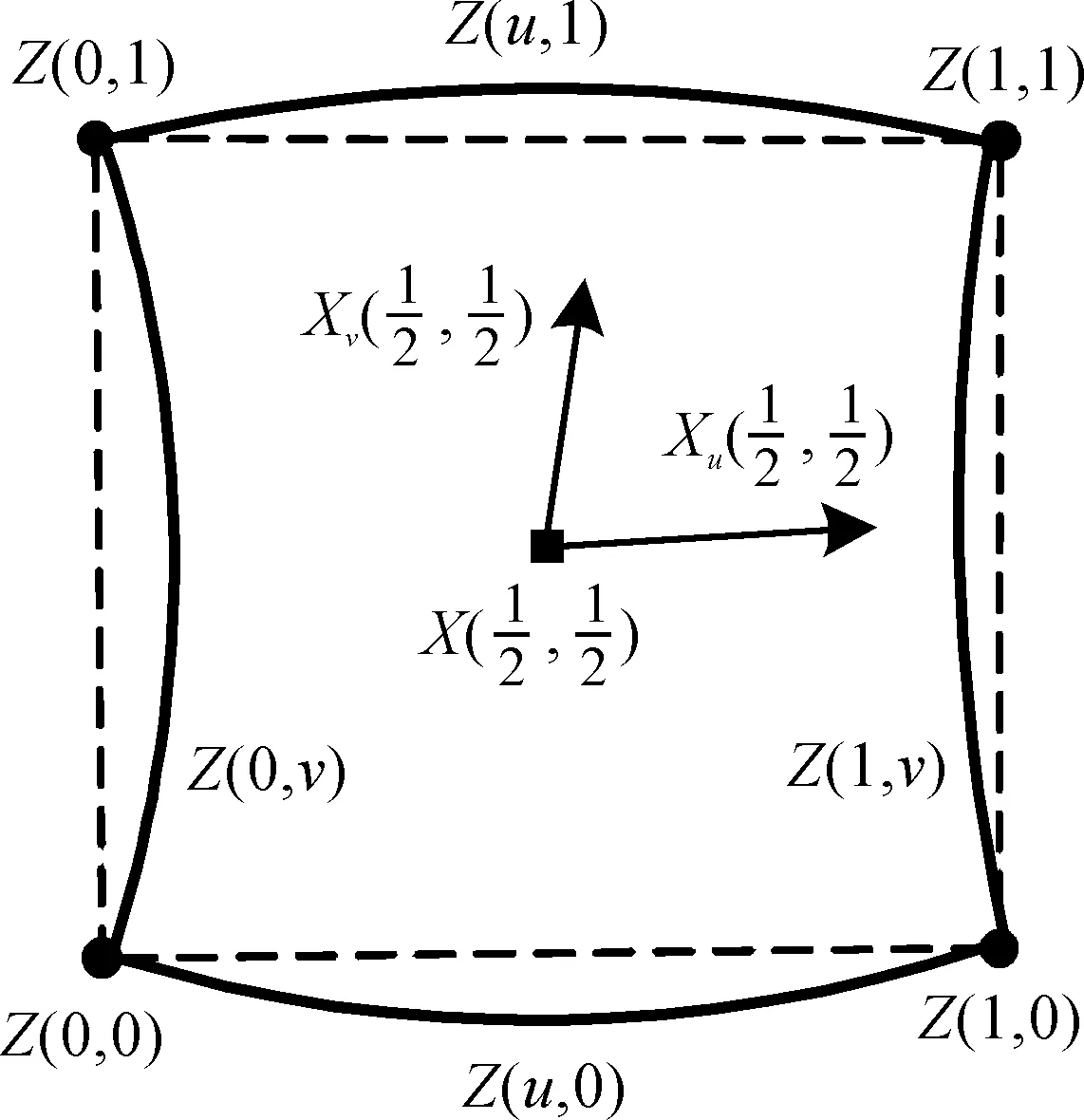
图3 新面点的计算示图

2.3 边界新边点跨界切向的计算

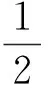
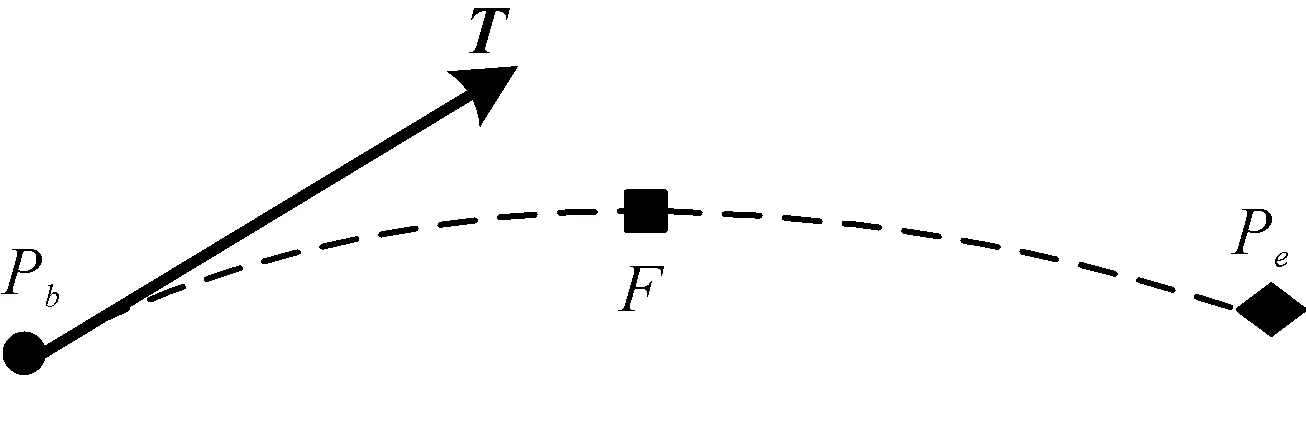
图4 边界新边点的计算示图

3 收敛性及光滑性分析

本文提出的基于Coons曲面的插值细分方法在任意一点处G1连续。细分过程中，任意一条旧边新插入的点皆通过构造相应的三次Bézier曲线采样得到，因此，只需证明任意两相邻点通过本文方法不断构造三次Bézier曲线插入新点得到的细分曲线收敛且G1连续，即可证明极限曲面的收敛性及光滑性。

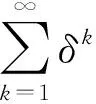
3.1 收敛性证明

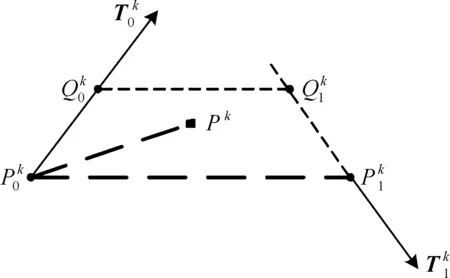
图5 收敛性证明

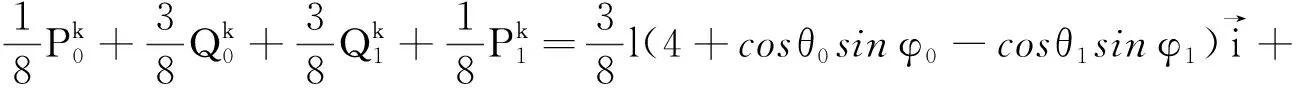
3.2 光滑性证明

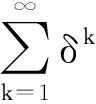
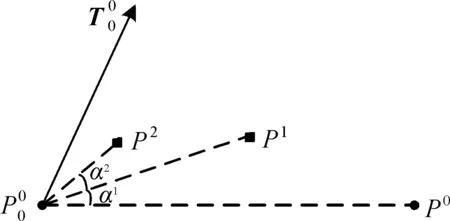
图6 光滑性证明

4 实例效果及分析

采用本文提出的基于Coons曲面的插值细分方法进行实验时，需给定初始网格点的切矢。初始网格的规则点需输入2个方向的初始切向，不规则点需设定更多方向的初始切向，手动给定所有点的初始切向过于不便，为此本文提出一种生成初始切向的方法。

(2)不规则点的处理。先确定不规则点的切平面。切平面的法向量包含此点所有四边形网格的单位法向量的均值；若四边形网格4个顶点不共面，则取四边形网格上该点及与其相邻两点所在平面的法向量，然后不规则点的各沿边切向取为各边在切平面上的单位投影向量。

本文细分方法在点插值的基础上也能保证切向插值，所以能够保证形状可调控及造型更自由的特点。用本文方法设计插值曲面时，可在待插值点处先选定好所期望的切平面，初始网格在该点处的切向若皆选自于所期望的切平面，则极限曲面在该插值点处的切平面即为所选定的切平面。

采用本文方法生成网格点初始切向的细分实例如图7所示，图7中部分细分实例所对应的斑马纹理图和高斯曲率图如图8所示。

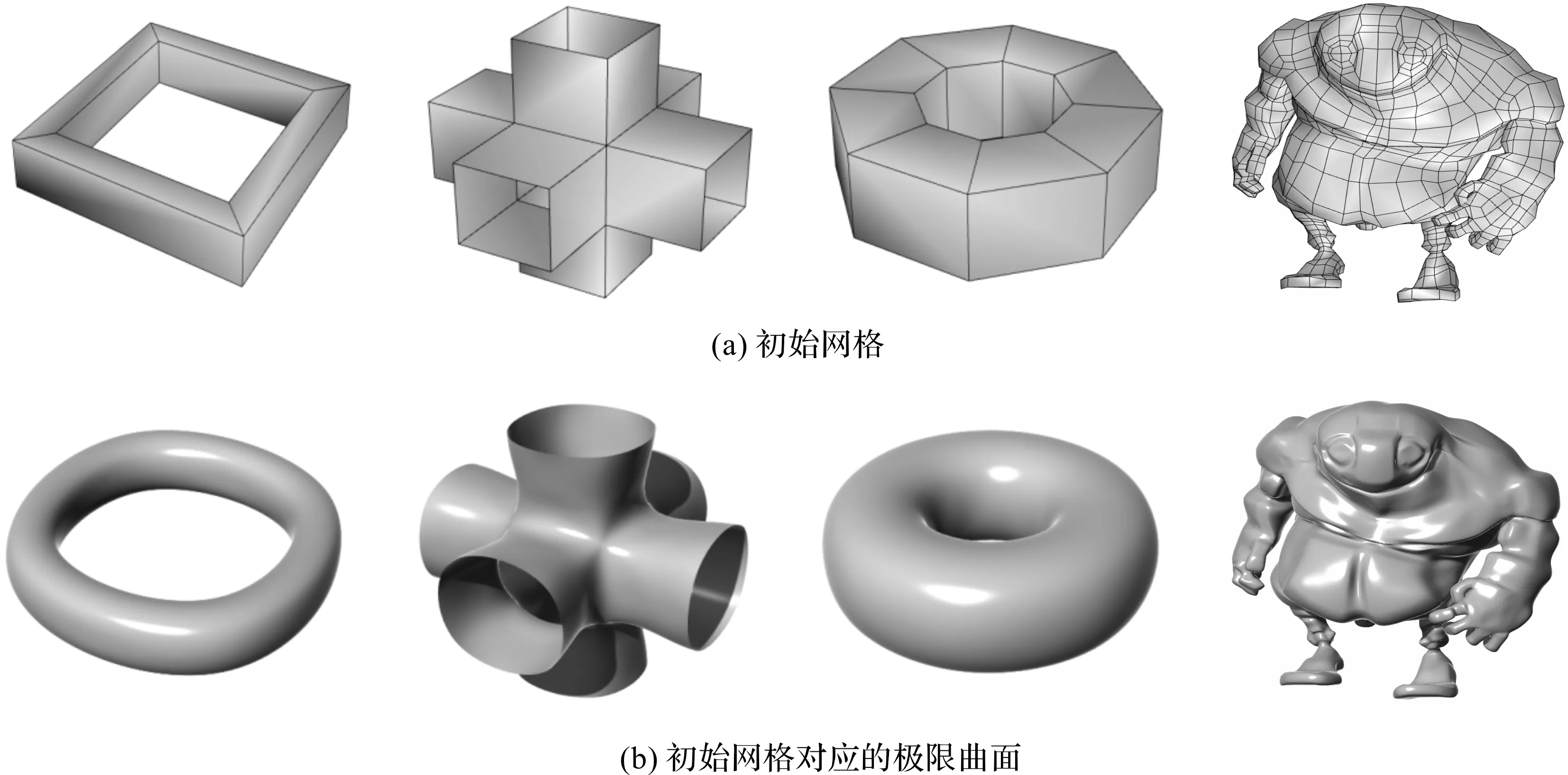
图7 初始网格及其极限曲面

图8 斑马纹理图和高斯曲率图

Kobbelt细分方法[7]作为经典的点插值细分方法，常应用于细分曲面。分别采用本文提出的基于Coons曲面的插值细分方法和Kobbelt细分方法进行实验，实例效果如图9所示。

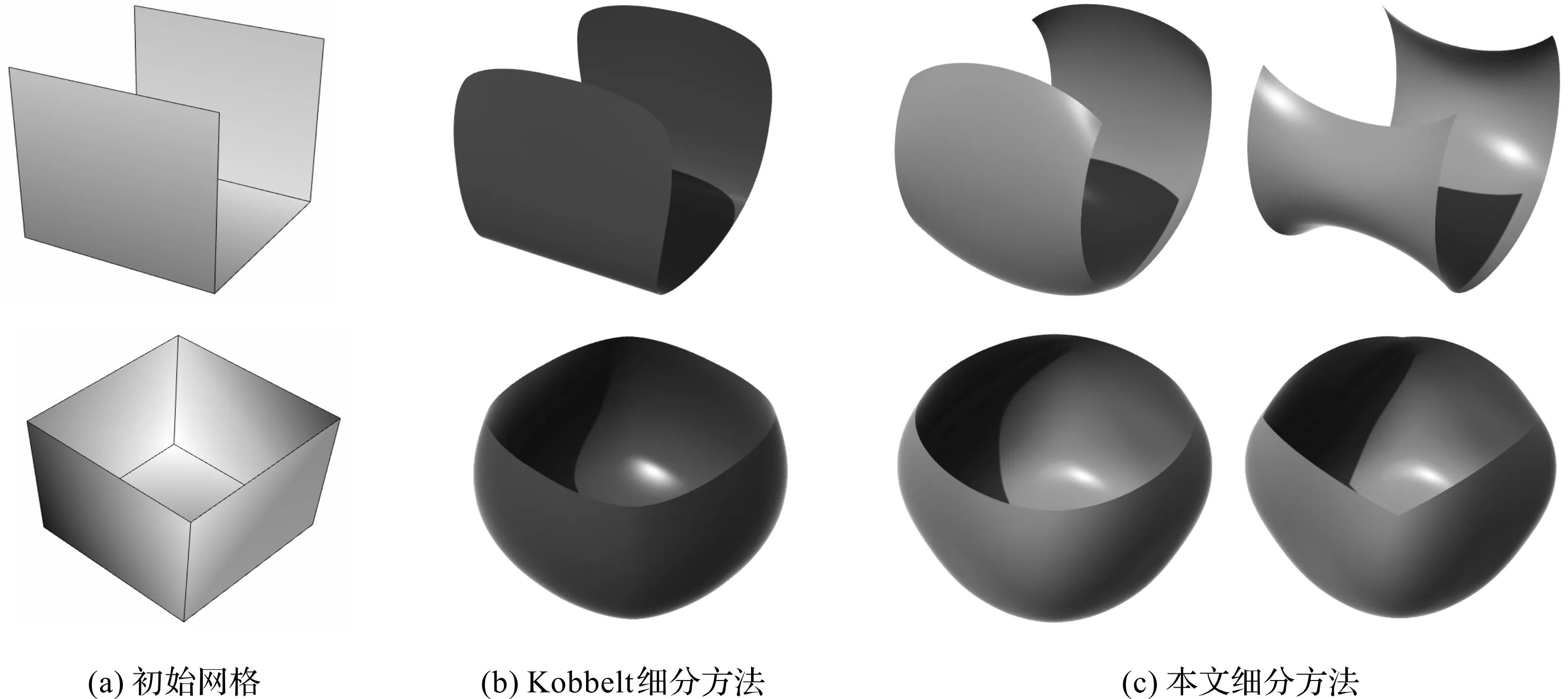
图9 不同细分方法的极限曲面

从图9可以看出，在不改变初始网格点的位置前提下，Kobbelt细分方法极限曲面的形状是固定的，而本文细分方法通过调整初始点的切向，达到调整极限曲面形状的效果。这是因为本文细分方法的初始网格每个点皆可选取满足需要的切向，额外自由度可调整插值曲面的形状，使得造型更加灵活自由。

5 结束语

经典插值型细分方法在不改变初始网格点位置的前提下，不便调整曲面的局部形状，为此，本文提出一种带切向的插值细分方法，简单易实现，造型灵活自由，得到效果不错的插值曲面。但是，在初始网格点切向选取较为极端或初始网格过于复杂的情况下，极限曲面可能出现自相交的情况，光滑性有待进一步提高，如何改进细分规则以改善这些问题是下一步研究的重点。