{1,2}-赋权图最小最大2-路径覆盖问题的近似算法
2022-10-10姚会影陈光亭
姚会影,周 圆,陈光亭,陈 永,张 安
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.台州学院电子与信息工程学院,浙江 台州 318000)
0 引 言
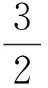
1 问题描述
边赋权完全图上的旅行售货商问题与最小最大2-路径覆盖问题定义如下:给定一边赋权完全图G=(V,E),其中|V|=n,边e∈E的权重为w(e)。TSP问题的目标是寻求覆盖G中所有顶点的一个圈,使得圈中各边的权重之和尽可能小。最小最大2-路径覆盖问题的目标是寻求覆盖G中所有顶点的2条顶点互不相交的路径,使得权重较大的路径的权重尽可能小,其中路径的权重是指路径中所有边的权重之和。
本文研究边权重为1或2的完全图上最小最大2-路径覆盖问题,即G中各边权重需满足:
w(e)∈{1,2},∀e∈E
(1)
对于该问题,当n≤6时,问题规模较小,通过穷举法就能得到最优解。因此,本文仅对n≥7的情况来设计近似算法。
2 算法设计与分析
本文设计的近似算法主要基于文献[4]提出的TSP算法,将其命名为基于TSP的近似算法。首先调用文献[4]关于TSP问题的算法,找到覆盖G中所有顶点恰好一次的圈C;然后删除圈C中2条不相邻的边,构成2条顶点不相交的路径P1和P2,为了使得其中的最大路径权重尽可能小,删边时应确保P1和P2的权重尽量均衡。当圈C中的边权重均为1时,删边过程是简单的;当圈C中包含至少1条权重为2的边时,本文算法采取一种贪婪的删边方法,具体步骤如下。
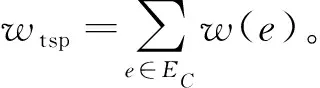
(2)在圈C中任选一条权重为2的边,记为e1。从边e1出发,按顺时针顺序对圈中各条边进行编号,记EC={e1,e2,…,en},删去圈C中的边e1。
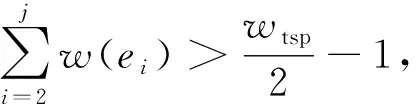
(4)将由边集{e2,e3,…,ej-1}构成的路径记为P1,由边集{ej+1,ej+2,…,en}构成的路径记为P2。
(5)比较路径P1和P2的权重,输出权重较大的路径P作为算法解。
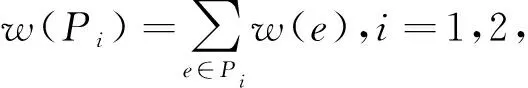
w(P)=max{w(P1),w(P2)}
(2)
(3)
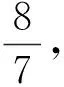
(4)


(5)
由式(1)可得:
(6)
由式(3)、式(5)、式(6)可得:
(7)
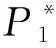
w(P*)≥3
(8)
证明由P1={e2,e3,…,ej-1},P2={ej+1,ej+2,…,en},3≤j≤n-1,可得:
(9)
由于路径P1,P2和边e1,ej构成圈C,有
w(P1)+w(P2)+w(e1)+w(ej)=wtsp
(10)
由本文算法的步骤3可得:
(11)
(12)
由式(10)、式(11),及w(e1)=2,可得:
(13)
由式(4)、式(12)、式(13),知
(14)
由式(7)、式(8)、式(14),知
为了便于理解本文提出的基于TSP的近似算法,通过1个算例来详细阐述算法的执行过程,如图1所示。图1中,实线表示权重为2的边,虚线表示权重为1的边,其中未画出的边权重均为1。
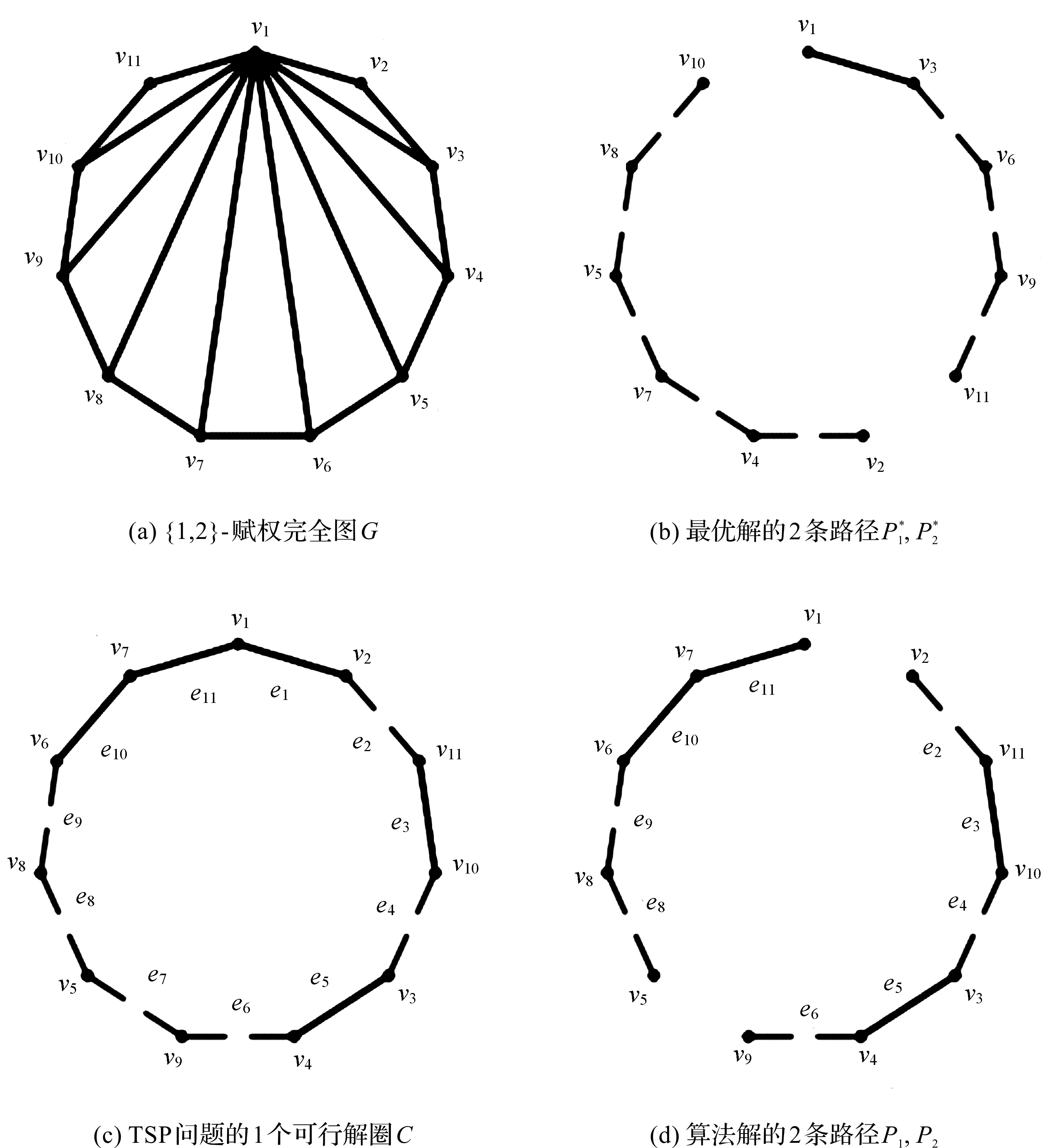
图1 图G、最优解、圈C及算法解图
假设1个顶点数n=11的{1,2}-赋权完全图G=(V,E),如图1(a)所示。其中V={v1,v2,…,v11},G中各边权重定义如下:w(vi,vi+1)=2(i=1,2,…,10),w(v1,vj)=2(j=3,4,…,10),其余各边权重均为1。

3 结束语

