Markov转换向量自回归模型的变分贝叶斯推断

吕秀丽，虞栋杰，郑 静

(杭州电子科技大学经济学院，浙江 杭州 310018)

0 引 言

研究变量间相互依赖关系的时间序列是较为经典的统计分析方法，其中向量自回归模型(Vector Autoregressive Models, VAR)是常用的计量经济模型。使用VAR模型对时间序列进行分析时，需先假设时间序列线性同质，但在实际应用中，各种复杂因素致使线性假定成立模型的分析结果不够准确。为了解决这个问题，学者们将研究方向转向非线性模型，龙如银等[1]运用区制为3、滞后阶数为1的Markov区制转换模型(Markov Switching Models, MS)研究我国1984年至2003年的通货膨胀率，与传统VAR模型相比，更好地拟合了我国经济的通货膨胀率。刘金全等[2]运用Markov转换向量自回归(Markov Switching-Vector Autoregressive Models, MS-VAR)模型将我国通货膨胀率分为3个区制，分析经济政策与通货膨胀率在各区制下的关系，合理解释了当时我国社会经济及通货膨胀风险状况，指出治理国家通货膨胀应先判断其所处区制。朱慧明等[3]引入贝叶斯MS-VAR模型，2次调用Gibbs抽样方法，研究我国股市与通货膨胀率的波动关系，指出可通过机制转换模型来刻画该波动关系。以上模型的参数较多，需事先进行参数估计。目前常用的模型参数估计方法有2类，一是确定性方法，如极大似然估计、EM算法等，在估计过程中未考虑模型参数的先验信息；二是贝叶斯方法、蒙特卡罗法等，计算成本较高，易产生过拟合或欠拟合。变分贝叶斯(Variational Bayes,VB)是贝叶斯推理的近似方法。Adami[4]将变分方法应用到贝叶斯推理中，介绍了如何用变分方法来逼近这类推理中出现的难以处理的后验分布；Alan等[5]采用参数扩展变分贝叶斯方法解决了VB收敛到近似解较慢的问题；Ormerod等[6]将变分近似引入统计学，用统计学术语解释变分近似概念；Koop等[7]提出一种均值场变分贝叶斯算法，分析美国宏观经济数据，将其拓展至计量经济学领域；马占宇等[8]结合变分推断，提出一种学术研究热点关键词提取方法，高效、准确地提取学术研究的热点关键词；沈圆圆等[9]提出一种Logistic组稀疏性回归的Bayes概率模型的变分贝叶斯算法，提高了模型的预测性能；万志成等[10]建立了一种无限变量高斯混合模型，解决了无限变量高斯混合模型的参数估计问题；付维明等[11]运用扩散方法对分布式随机变分推断算法进行改进，并将其应用至主题模型，速度快，可扩展强。本文提出一种Markov转换向量自回归模型的变分贝叶斯推断算法，利用参数的先验信息对MS-VAR模型的参数进行估计，并给出完整的变分推理过程。

1 MS-VAR模型

1.1 马尔可夫转移模型

给定所有先前的状态，马尔可夫链(本文简称马氏链)的当前状态依赖且仅依赖其前一个状态，这一性质被称为马尔可夫特性。马尔可夫区制转移模型依赖具有马尔可夫性的马氏链生成的随机过程。

设{yt,t=1,…,T}为具有T个单变量观测值的时间序列，是随机过程{yt}的子集。隐藏的离散随机过程{zt}的实现决定了随机过程{yt}的概率分布。{yt}是直接可观测的，而{zt}是一个潜在的随机变量，只能通过观测{yt}来间接观测过程{zt}。假设隐过程{zt}是一个具有有限状态空间{0,…,K-1}的不可约、非周期的马氏链，其随机性质用K×K阶转移矩阵A描述，其中aij是转移矩阵A的第i+1行第j+1列元素，表示在t-1时刻处于状态i，下一时刻转移到状态j的概率。转移矩阵A中每一行的所有元素之和为1且所有元素非负，即：

设参数θi∈Θ是由转移区制决定的参数，而ψ∈Ψ是不依赖于区制的参数，Θ,Ψ为参数空间，θi和ψ共同决定了参数条件密度p(·|θi,ψ|)。本文假设在给定z1,…,zΤ时的随机变量y1,…,yΤ是条件独立的，其密度为：

yt|(zt=i)|～p(·|θi,ψ|)

对于联合随机过程{zt,yt}，yt的条件密度为：

其中，It-1={yt-1,yt-2,…}为t-1时刻可获得的观测信息。

1.2 马尔可夫区制转移的向量自回归模型

假设yt=(y1t,y2t,…,ymt)′为m×1的观察值向量，随机变量st=1,2,…,J(J≥2)表示在t时刻的状态，与误差向量εst独立，误差向量εst服从均值为0且协方差阵为Σst的正态分布，存在一个初始状态概率向量为Π、状态转移概率矩阵为A的马氏链，St={s1,s2,…,st}是由该马氏链生成的不可观测的随机状态序列，

Π=(πj),πj=p(s1=j),1≤j≤J；

A=(aij),aij=p(st=j|st-1=i|),1≤i,j≤J,1≤t≤T

其中，πj为初始状态为j的概率。Ust为st状态下的均值向量，故MS-VAR模型的向量形式为：

其中，yt∈Rm，α1,st,…,αd,st∈Rm×m表示自回归系数，d为模型的滞后阶数，εst∈Rm。

设Ωst=[Ust,α1,st,…,αd,st]′∈R(md+1)×m，xt=[1,yt-1,…,yt-d]′∈R(md+1)×1，故MS-VAR模型改写成为：

yt=Ω′stxt+εst

进一步转化为：

Y≈XΩst

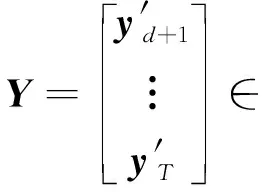
根据以上参数的相关假设可以得到yt～Nm×1(Ω′stxt,Σst)，则向量yt的条件概率密度分布函数为：

其中，Φt-1为变量参数集合，包含t-1时刻所有参数的信息。

2 变分贝叶斯推断

贝叶斯估计方法通过设置参数的先验分布，根据贝叶斯规则，利用样本信息推导出参数后验分布，得到参数估计值。但是，由于大部分真实后验概率的积分表达式难以简化计算，估计工作无法顺利进行。本文运用变分法来逼近后验概率，其关键思想是选择一系列易于操作的分布族来逼近真实的后验概率。

假设Ω=(Ω1,Ω2,…,ΩJ)是待估参数向量，对于一个给定的模型设计参数Φ1={Ω,Σ}，Φ2={Π,A}，完整数据的似然函数为：

p(Y,S|Φ1,Φ2|)=p(Y|S,Φ1|)p(S|Φ2|)

(1)

其中，

(2)

(3)

根据贝叶斯规则，边际似然函数为：

(4)

此时，隐式变量和模型参数都被视为随机变量，假设隐变量和模型参数的变分后验分布为q(S,Φ1,Φ2)，结合式(4)可得对数边际似然函数，

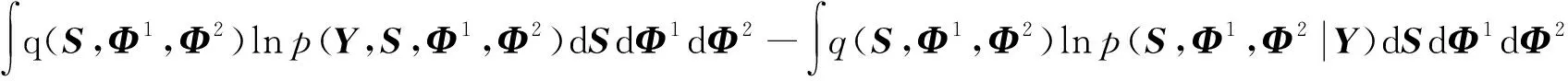
(5)

进一步整理式(5)，可得：

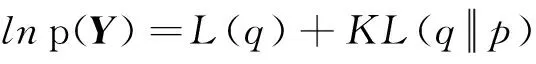
其中，

(6)

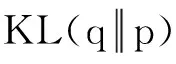
为了计算变分的下界L(q)，需要指定变分后验概率的形式和模型参数的先验分布。本文中，变分后验概率的因式分解形式如下：

q(S,Φ1,Φ2)=q(S)q(Π)q(A)q(Ω,Σ)

(7)

为了简便计算，需要先验分布和后验分布的形式保持高度一致。设Π和Α矩阵中每一行的先验分布为狄利克雷(Dirichlet Distribution, Dir)分布，即

(8)

(9)

文献[12-13]认为，参数Ω的先验分布为正态-逆Wishart分布，即

(10)

式中，

(11)

(12)

式中，W-1表示逆Wishart分布。

模型参数的先验分布表示为：

p(Φ1,Φ2)=p(Ω,Σ)p(Π)p(Α)

(13)

此时，变分下界L(q)可通过式(6)求解，将式(6)改写为：

L(q)=Eq[lnp(Y,S,Φ1,Φ2)]-Eq[lnq(S,Φ1,Φ2)]

(14)

式中，E(·)表示期望，将式(1)—式(3)、式(7)—式(13)代入式(14)，可得：

Eq[lnp(Y,S,Φ1,Φ2)]=Eq[lnp(Y|S,Φ1)+lnp(S|Φ2)+lnp(Φ1)+lnp(Φ2)]=

(15)

Eq[lnq(S,Φ1,Φ2)]=E[lnq(S)+lnq(A)+lnq(Π)+lnq(Ω,Σ)]

(16)

式(15)中，δ(·)表示δ函数，当s(t-1)i与stj的乘积为1时，δ(·)为1，否则为0。

在变分贝叶斯的框架下，变分后验概率的近似最优解为：

lnqg(Zg)=Eh≠g[lnp(Y,Z)]+C

(17)

式中，Z={S,Φ1,Φ2}表示状态变量和参数的集合，Zg表示集合Z中第g项参数，不涉及Zg参数的项均视为常数，记作C。求解参数Zg的变分后验时，将除Zg外的参数视为随机变量，参数Zg视为固定变量，对式(17)中与Zg参数相关、但不等于参数Zg的项进行计算，得到随机变量的数学期望Eh≠g[lnp(Y,Z)]。

3 变分后验分布

运用式(17)对模型中的各个参数进行变分推断，求解参数的变分后验分布，并利用后验分布计算变分下界。

3.1 q(Π),q(A)变分推断

求解变分后验概率q(Π)时，将Π视为一个参数，其余的S,A,Ω,Σ视为随机变量，因此与Π无关的项即为常数。将所有与Π相关的项合并在一起，计算结果如下：

lnq*(Π)=ES,A[lnp(S|Π,A)]+lnp(Π)+C=

(18)

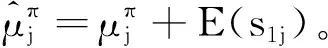
同理，可以计算出q(A)，

lnq*(A)=ES,Π[lnp(S|Π,A)]+lnp(A)+C=

(19)

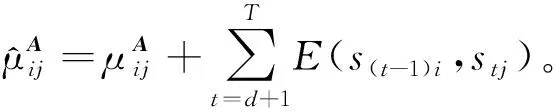
3.2 q(Ω,Σ)变分推断

将所有与Ω,Σ相关的项整合在一起，得到：

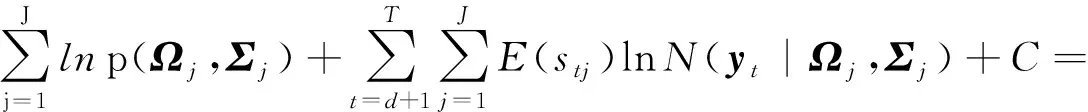
(20)

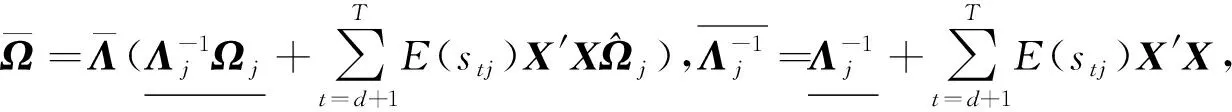
3.3 q(S)变分推断

将所有与隐变量S相关的项整合，得到：

lnq*(S)=EΠ,A[lnp(S|Π,A)]+EΩ,Σ[lnp(Y|S,Ω,Σ)]+C=

(21)

对于隐马尔可夫模型，隐变量q(S)变分后验的主要形式为：

(22)

比对式(21)和式(22)，可得：

(23)

(24)

(25)

在得到q(S)的分布后，计算得出隐变量的单点均值ES(stj)和两点均值ES(s(t-1)i,stj)，

(26)

(27)

式中，fvar(·)为前向概率，bvar(·)为后向概率。

3.4 变分下界L(q)

结合隐变量和参数的先验分布，运用变分贝叶斯方法推导出隐变量和参数的变分后验分布后，将式(18)—式(27)代入式(14)，计算得出的变分下界如下：

L(q)=E[lnp(Π)]+E[lnp(A)]+EΩ,Σ[lnp(Ω,Σ)]+

ES,Ω,Σ[lnp(Y|S,Ω,Σ)]+ES,Π,A[lnp(S|A,Π)]-

E[lnq(S)]-E[lnq(A)]-E[lnq(Π)]-E[lnq(Ω,Σ)]

(28)

式中，

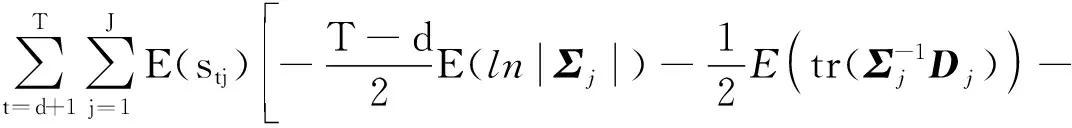
(29)

(30)

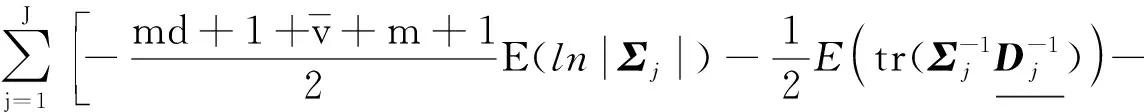
(31)

(32)

(33)

(34)

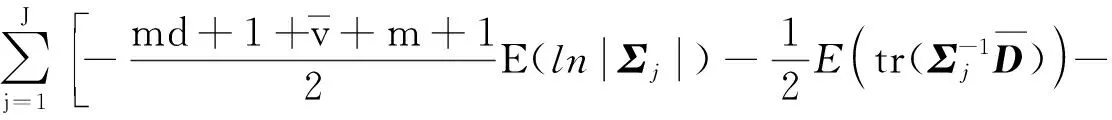
(35)

(36)

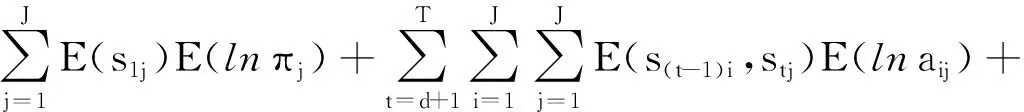
(37)

将式(29)—式(37)代入式(28)，可得：

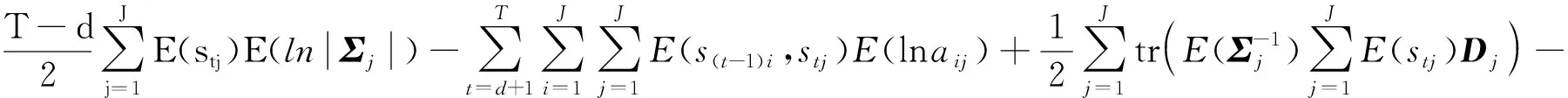
根据狄利克雷分布的性质，计算得出的相应期望如下：

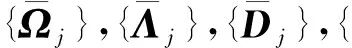
4 实证分析

4.1 数据选取与处理

本文从我国国家外汇管理局门户网站选择人民币兑美元汇率中间价历史数据，从网易财经官网选择上海证券综合指数(简称上证综指或沪指)、深圳证券成份指数(简称深证成指)的历史交易日度数据，组成一个3变量原始样本，数据采集时间从2015-01-05日至2021-06-30，根据金融行业交易特点即有交易日与非交易日之分，剔除非交易日后共收集到1 580组数据。人民币兑美元汇率的收益率可由汇率中间价时间序列数据经过计算而得，计算公式如下：

Rt=100×(lnrt-lnrt-1)

式中，rt为当日汇率的中间价，Rt为处理后的汇率收益率，自然对数用于消除系列的不稳定性，为了更好地减少误差，其百分比形式需要乘以100。

用相同原理处理沪指和深证成指数据，得到相应的收益率。本文用Rratio表示人民币兑美元汇率中间价的日对数收益率、Rsz表示上证综合指数的日对数收益率、Rsc表示深证成分指数的日对数收益率。

对模型设计参数进行分析估计前，先绘制3组日对数收益率数据的时间序列图，判断其经济平稳性。时间序列图如图1所示。

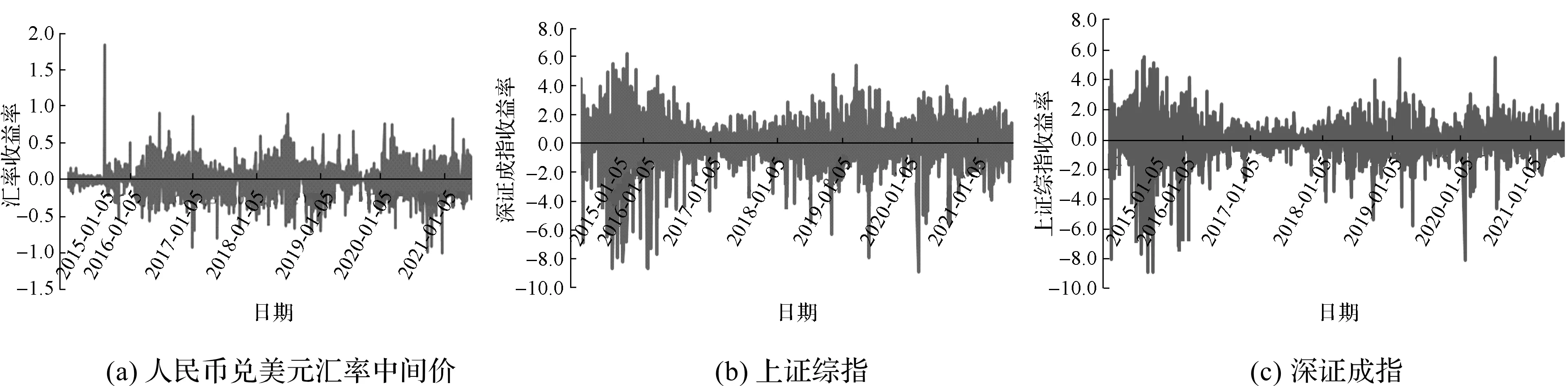
图1 3组日对数收益率的时间序列图

从图1可以看出，3组对数收益率曲线均围绕0值上下波动，除图1(a)中出现1个异常点外，其余部分波动幅度前后、上下一致，故认为是平稳序列。由于图检验法具有较强的主观性，为了确保检验结果的稳健性，使用Eviews10.0软件进行增广迪基-富勒(Augmented Dickey-Fuller, ADF)检验和菲利普斯-珀森(Phillips-Perron, PP)检验。ADF检验和PP检验的零假设H0均为存在单位根，区别在于两者的检验统计量不同，如果序列平稳，则该序列不存在单位根。当显著性水平为α时，检验统计量小于该水平下的迪基-富勒(Dickey-Fuller, DF)临界值，此时应该拒绝原假设，在α显著性水平下认为该序列平稳。3组日对数收益率的检验结果如表1所示。

表1 不同对数收益率的平稳性检验

表1中，变量Rratio的ADF值为-36.520 76，显著性水平1%DF临界值为-3.434 157，其ADF值小于显著性水平1%DF临界值，且Rratio相应的PP统计量值为-36.794 94，同样小于1%DF临界值，表明拒绝原假设，故认为变量Rratio为平稳序列。同理可得，变量Rsz和Rsc拒绝原假设，因此，3组参数变量均为平稳序列。

4.2 参数估计

在建立模型之前，需要选择合适的模型参数。在选择时滞顺序时，应考虑模型的整体动态性和自由度。阶数较大时，可以更好地反映一个模型研究动态性，但自由度会减少，需要估计的参数会增加。通常情况下，滞后阶数的确定根据赤池信息准则(Akaike Information Criterion , AIC)、施瓦茨准则(Schwarz Criterion, SC)、汉南-奎因准则(Hannan-Quinn Criterion, HQ)和最终预测误差准则(Final Prediction Error, FPE)来进行综合判断，准则的值越小，表明模型拟合效果越好。为了选取合适的滞后阶数，运用Eviews10.0软件对3组对数收益率数据做VAR分析，结果如表2所示。

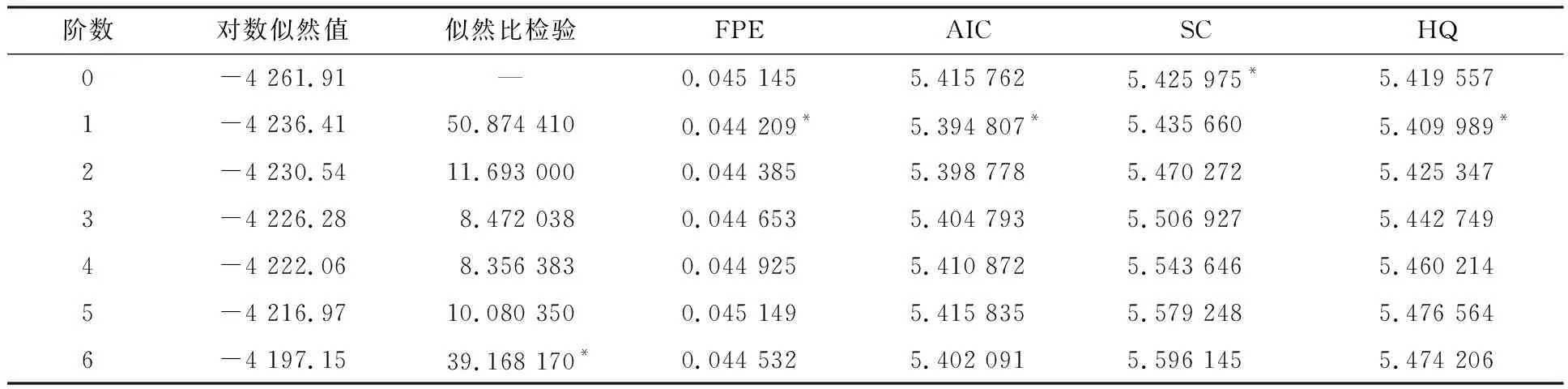
表2 不同准则下的滞后阶数

从表2可以看出，在滞后阶数为1时，其FPE，AIC与HQ准则的值均达到最小，表明该准则下的最优滞后期为1。本文经过综合分析，选取MS-VAR模型的滞后阶数为1。

由于本文研究的参数是人民币兑美元汇率及沪深指数，分析时结合其经济发展意义，将马尔可夫的区制即状态变量设为2，即划分为汇率上升或汇率下降这2种不同体制。假设d=1,j=2，状态变量为st，MS-VAR模型表示为：

(38)

由式(38)可以看出，模型中有28个待估计参数。进行模型估计时，若待估参数过多，一方面会增加估计成本，另一方面预测效果并不一定能达到预期，甚至可能偏离经济理论。本文提出的Markov转换向量自回归模型的变分贝叶斯推断算法使得参数估计变得更加精确，且收敛速度较快，节约了时间成本。

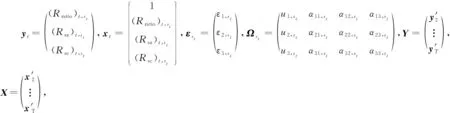
取T=1 580，运行MATLAB R2018a软件，使用本文提出的Markov转换向量自回归模型的变分贝叶斯推断算法迭代1 000次，并针对迭代结果，计算样本均值的标准差，即标准误，得到模型转移概率的估计结果如表3所示。

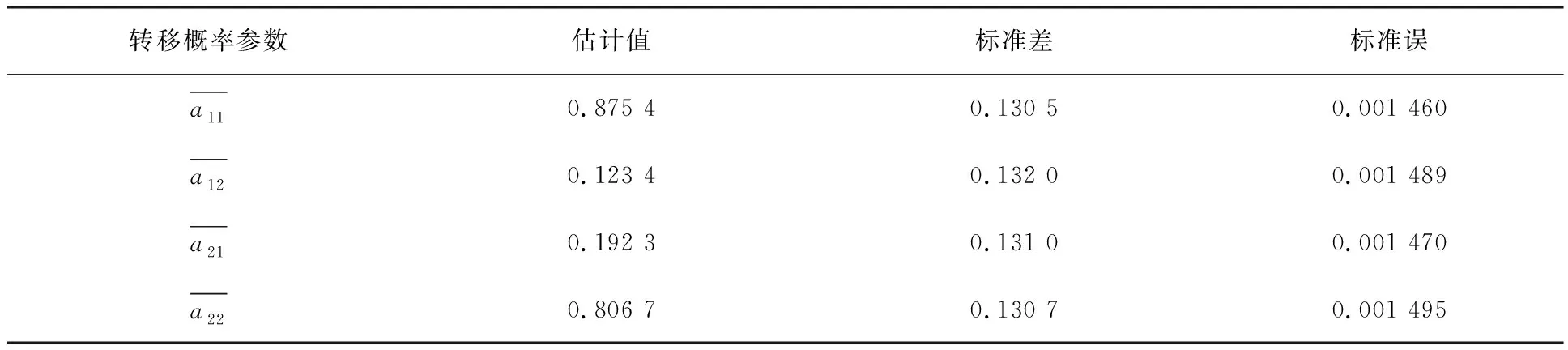
表3 转移概率的估计结果

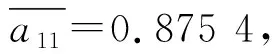
迭代后得到模型参数矩阵的估计结果是：

5 结束语

针对Markov转换向量自回归模型应用传统参数估计方法成本高、易过拟合等缺陷，本文在变分贝叶斯的理论框架下，提出一种Markov转换向量自回归模型的变分贝叶斯推断算法。详细演算MS-VAR模型的变分推导过程，给出参数估计算法，并结合实证分析验证了本文算法在高维数据结构情形下的高收敛性。但是，本文模型中存在多个系统，难以将观测值划分为各状态参数，无法估计所有系统的参数，下一步计划将支持向量机、逻辑回归等机器学习分类方法与MS-VAR模型变分贝叶斯方法结合起来，研究模型中不同区制的区分及其参数估计。