忆阻器网络等效分析电路及其特性研究
2012-09-19何宝祥包伯成
何宝祥 包伯成
(常州大学信息科学与工程学院 常州 213164)
1 引言
根据电路基本变量组合完备性原理,1971年美国加州大学伯克利分校的华裔科学家蔡少棠[1](Chua L O)预测了直接关联电荷和磁通两个变量的基本电路元件忆阻器的存在性。忆阻器是一种具有非易失记忆功能的非线性无源器件[2,3],它是除电阻器、电容器和电感器之外的第4种基本电路元件。但直到2008年,惠普实验室才成功制作出了基于金属和金属氧化物的忆阻元件,并建立了忆阻器的数学模型[4]。自此,人们在忆阻器的物理构造、基本特性和应用等方面开展了卓有成效的研究工作,如基于半导体纳米技术实现具有不同特性的忆阻器的研究[5,6];基于忆阻器的基本电路特性的研究,包括忆阻器的电路建模[7]、SPICE宏建模[7-11]、伏安特性分析[1,2,12-14]以及等效电路实现[15,16]等;基于忆阻器的各种应用电路设计及其相应的系统特性的理论分析和数值仿真方法的研究[17-24]。忆阻器及其所组成的简单应用电路都可以通过状态方程建模进行仿真或实验分析,文献[8]所建模型着重分析忆阻器的伏安特性;文献[9]所建模型着重分析了忆阻器的边界特性;文献[10]所建模型能高速模拟磁控忆阻器在高磁场条件下动力学行为。大多所建模型或稳定性差,或结构复杂,或精度较低。何况忆阻器是一个有边界条件约束的强非线性无源器件,其所组成的忆阻器网络更是一个非常复杂的非线性问题,因此忆阻器网络建模很少有人问津。
本文提出了忆阻器有P型和N型两种基本模型,它们具有对偶的物理特征,因而将它们通过适当的连接和参数的设置,所得到的忆阻器网络对外可以等效为线性网络,但就每个忆阻器本身而言仍然具有非易失和非线性等典型特征。为证明起见,文中分别给出了单个P型和N型忆阻器以及忆阻器串并联的等效分析电路的拓扑结构,并用具体电路进行了验证。
2 忆阻器基本特性及其分析电路
图1所示为惠普实验室制作的忆阻器基本模型。

图1 忆阻元件的基本模型
图1中D为忆阻元件的长度,w(t)表示元件的掺杂区域的宽度。掺杂部分的电阻率小于未掺杂部分的电阻率。元件总电阻r(t)等于掺杂部分电阻与未掺杂部分电阻的阻值之和。经研究可知,忆阻元件上流过的电流i(t)与w(t)变化率成线性关系[3]。忆阻器数学模型[4]为

其中Roff为元件全部未掺杂情况下,即w(t)=0时的电阻值;Ron为元件全部掺杂情况下,即w(t)=D时的电阻值;μv为表示离子在均匀场中移动情况的常数。由于掺入不同杂质后可形成正负两种离子,故存在两种忆阻器分别代表了μv>0和μv<0的情况,不妨称μv>0忆阻器为P型忆阻器,μv<0忆阻器为N型忆阻器。
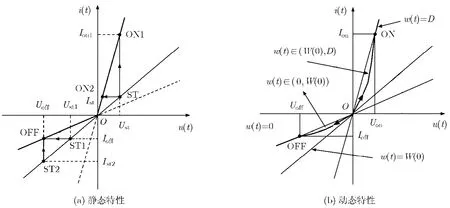
图2 P型忆阻器伏安特性
就P型忆阻器而言,若w(t)∈(0,D),且当u(t)>0时,i(t)>0,掺杂区域向右扩展,w(t)增大,r(t)变小;当u(t)>0时,i(t)<0,掺杂区域向左收缩,w(t)减小,r(t)变大;当u(t)=0时,i(t)=0,掺杂区域不变,w(t)和r(t)均保持不变。显然,在w(t)∈(0,D)条件下忆阻元件具有记忆特性。但在w(t)=0和w(t)=D条件下,忆阻元件分别工作两种极限情况,相当于一个不同阻值的线性电阻。
忆阻器在不同的激励条件下有不同的伏安特性,P型忆阻器常见的伏安特性如图2所示。图2(a)细实线为起始边界,粗实线为终止边界,其间为忆阻器工作区,其中第1象限为正向工作区,第3象限为反向工作区。图2(a)反映了忆阻器的静态伏安特性:ST→ON1为忆阻器恒定正向电压激励下的情况,忆阻器阻值逐步减小,流过的电流由Ist逐步增加到Ion1,并最终稳定工作于ON1点上;ST→ON2为忆阻器恒定正向电流激励下的情况,忆阻器阻值同样逐步减小,两端的电压由Ust逐步减小到Uon2,并最终稳定工作于ON2点上; ST1→OFF为忆阻器恒定反向电流激励下的情况,忆阻器阻值逐步增大,两端的电压由Ust1逐步增大到Uoff,并最终稳定工作于OFF点上;ST2→OFF为忆阻器恒定正向电压激励下的情况,忆阻器阻值同样逐步增大,流过的电流由Ist2逐步减小到Ioff,并最终稳定工作于OFF点上。
图2(b)反映了忆阻器的动态伏安特性。设t=0时,忆阻器w(t)=W(0),则正向工作且在w(t)∈(W(0),D)条件下,忆阻器为具有记忆特性的非线性器件,流过的电流随电压的增加单调增加,且增加速度逐步加快,直至边界w(t)=D,此后忆阻器相当于一个阻值为Ron的线性电阻;反向工作且在w(t)∈(0,W(0))条件下,忆阻器同样是一个具有记忆特性的非线性器件,流过的电流随电压的增加单调增加,但增加速度逐步减缓,直至边界w(t)=0,此后忆阻器相当于一个阻值为Roff的线性电阻。
3 P型忆阻器的串联和并联等效电路模型
3.1 P型忆阻器的串联等效电路模型
P型忆阻器的串联有正向和反向两种串联方式。P型忆阻器流过电流时,掺杂区域变宽,称之为正向串联;P型忆阻器流过电流时,掺杂区域变窄,称之为反向串联。设有j个P型忆阻器串联,由基尔荷夫定律不难得到P型忆阻器串联的数学模型为

其中,正向串联时,kj=1;反向串联时,kj=-1。
由式(3)和式(4)可知,设P型忆阻器j(j=1,2,…,J)的基本模块Hj如图3所示,则j个P型忆阻器串联基本分析电路组成框图如图4所示。

图3 P型忆阻器串联型基本分析模块Hj

图4 j个P型忆阻器串联等效电路框图
3.2 P型忆阻器的并联分析电路模型
P型忆阻器的并联也有正向和反向两种方式。P型忆阻器流过电流时,掺杂区域变宽,称之为正向并联;P型忆阻器流过电流时,掺杂区域变窄,称之为反向并联。设有j个P型忆阻器并联,参照表达式(3)和式(4)可得P型忆阻器j(j=1,2,…,J)满足

其中,正向并联时,kj=1;反向并联时,kj=-1。
由式(5)和式(6)可得P型忆阻器j基本分析模型Sj如图5所示。由于j个P型忆阻器并联后流过的总电流,不难得到P型忆阻器的并联分析电路组成框图如图6所示。

图5 P型忆阻器并联型基本分析模型Sj

图6 j个P型忆阻器并联等效电路框图
这里需要说明的是,P型忆阻器的正向串联和正向并联与N型忆阻器的反向串联和反向并联相互等效;P型忆阻器的反向串联和反向并联与N型忆阻器的正向串联和正向并联相互等效。故N型忆阻器的串联和并联等效分析电路模型不再赘述。
4 忆阻器的等效电路及其特性仿真分析
4.1 单个忆阻器的等效电路
对于P型忆阻器,其典型等效电路如图7所示,经分析可知

图7 P型忆阻器等效电路
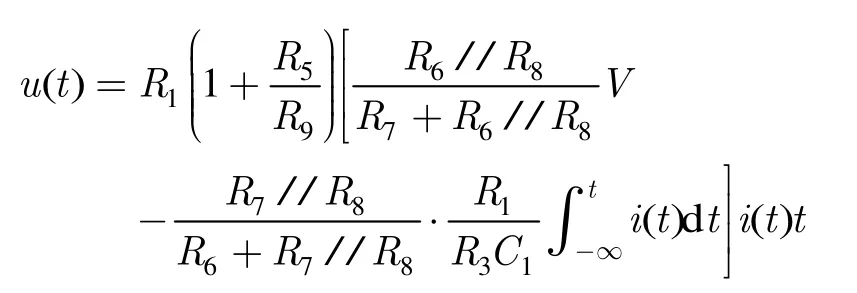
其中“//”为电阻并联运算符,对比式(1)和式(2),可见有相同的形式,电路参数可由忆阻器参数选定,即
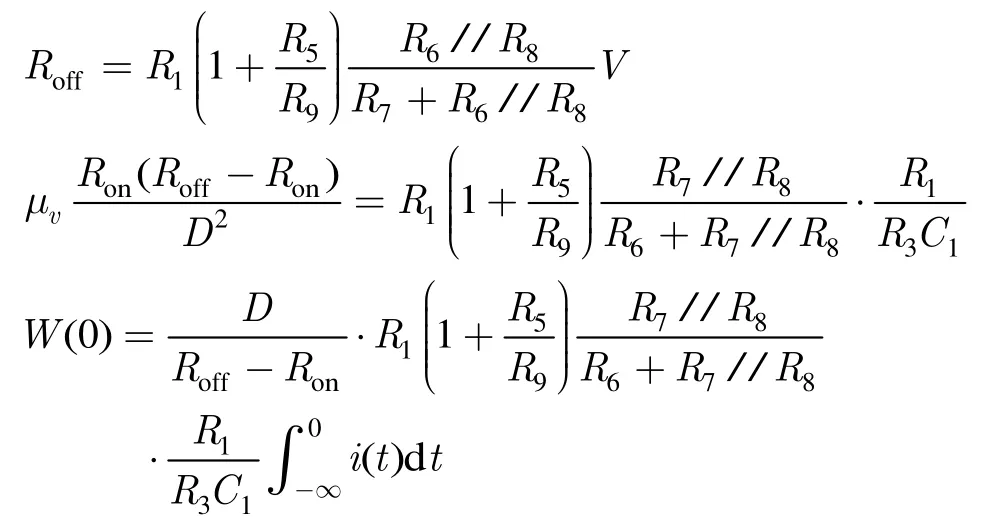
设i(t)=2sinωt(mA),则图7的转移特性和输出特性仿真结果分别如图8和图9所示,由文献[4]可知转移特性仿真结果准确表征了忆阻器的伏安特性。

图8 P型忆阻器伏安特性

图9 P型忆阻器输入i(t)与输出u(t)之间的关系

图10 N型忆阻器等效电路

图11 N型忆阻器伏安特性
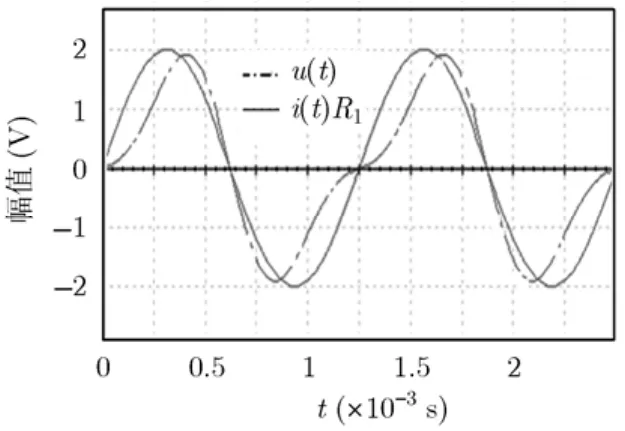
图12 N型忆阻器输入i(t)与输出u(t)之间的关系
对于N型忆阻器,其典型分析电路如图10所示,经分析可知

对比式(1)和式(2),可见同样有相同的形式,同理电路参数可由忆阻器参数选定。其模拟的忆阻器伏安特性和输入输出关系仿真结果如图10和图11所示。
4.2 忆阻器网络等效电路
忆阻器可以通过串联和并联等形式连接成忆阻器网络。图13为P型忆阻器与N型忆阻器串联电路,其输出特性如图14所示。从仿真结果可以看到,其非线性减弱,当两个忆阻器特性参数对偶时,串联后对外部网络而言相当于一个线性电阻,但各忆阻器本身固有属性不变。
5 结论
忆阻器有P型和N型两种,它们可以通过串并联连接成网络。对于其特性可以利用等效电路进行仿真分析。P型和N型忆阻器具有对偶特征,因此忆阻器间可以通过适当的拓扑连接和参数选择,对外呈现出线性特性,而各自仍具备忆阻器的固有性质。忆阻器等效电路的建立,为忆阻器网络的分析和设计及其理论和应用研究提供了一个有效途径。

图13 P型忆阻器与N型忆阻器的串联等效分析电路

图14 P型忆阻器与N型忆阻器串联输入i(t)与输出u(t)之间的关系
[1]Chua L O.Memrister—the missing circuit element[J].IEEE Transactions on Circuit Theory,1971,CT-18(5): 507-519.
[2]Chua L O and Kang S M.Memristive devices and systems[J].Proceeding of the IEEE,1976,64(2): 209-223.
[3]Strukov D B,Snider G S,Stewart D R,et al..The missing memristor found[J].Nature,2008,453(5): 80-83.
[4]Tour J M and H Tao.Electronics: the fourth element[J].Nature,2008,453(5): 42-43.
[5]Wang X,Chen Y,Xi H,et al..Spintronic memristor through spin torque induced magnetization motion[J].IEEE Electron Device Letters,2009,30(3): 294-297.
[6]Pershin Y V and Di Ventra M.Spin memristive systems: spin memory effects in semiconductor spintronics[J].Physical Review B,2008,78(11):113309.
[7]Martinelli G.Circuit modeling of nano-devices[J].Electronics Letters,2008,44(22): 1294-1295.
[8]Benderli S and Wey T A.On SPICE macromodelling of TiO2memristors[J].Electronics Letters,2009,45(7): 377-379.
[9]RakÁ and Cserey G.Macromodeling of the memristor in SPICE[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2010,29(4): 632-636.
[10]Biolek D and Biolkova V.Mutator for transforming memristor into memcapacitor[J].Electronics Letters,2010,46(21): 1428-1429.
[11]Biolek Z,Biolek D,and Biolková V.SPICE model of memristor with nonlinear dopant drift[J].Radioengineering,2009,18(2): 210-214.
[12]Joglekar Y N and Wolf S J.The elusive memristor: properties of basic electrical circuits[J].European Journal of Physical,2009,30(4): 661-675.
[13]Pershin Y V and Di Ventra M.Memristive circuits simulate memcapacitors and meminductors[J].Electronics Letters,2010,46(7): 517-518.
[14]Riaza R.Nondegeneracy conditions for active memristive circuits[J].IEEE Transactions on Circuits and Systems–II,2010,57(3): 223-227.
[15]Muthuswamy B and Chua L O.Simplest chaotic circuit[J].International Journal of Bifurcation and Chaos,2010,20(5):1567-1580.
[16]Muthuswamy B.Implementing memristor based chaotic circuits[J].International Journal of Bifurcation and Chaos,2010,20(5): 1335-1350.
[17]Witrisal K.Memristor-based stored-reference receiver–the UWB solution[J]?Electronics Letters,2009,45(14): 713-714.
[18]Itoh M and Chua L O.Memristor oscillators[J].International Journal of Bifurcation and Chaos,2008,18(11): 3183-3206.
[19]Muthuswamy B and Kokate P P.Memristor based chaotic circuits[J].IETE Technical Review,2009,26(6): 415-426.
[20]Bao B C,Liu Z,and Xu J P.Steady periodic memristor oscillator with transient chaotic behaviors[J].Electronics Letters,2010,46(3): 228-230.
[21]包伯成,刘中,许建平.忆阻混沌振荡器的动力学分析[J].物理学报,2010,59(6): 3785-3793 Bao B C,Liu Z,and Xu J P.Dynamical analysis of memristor chaotic oscillator[J].Acta Physica Sinica,2010,59(6):3785-3793.
[22]Bao B C,Xu J P,and Liu Z.Initial state dependent dynamical behaviors in memristor based chaotic circuit[J].Chinese Physical Letters,27,070504(2010).
[23]张旭,周玉泽,闭强,等.有边界条件的忆阻元件模型及其性质[J].物理学报,2010,59(9): 6673-6680.Zhang X,Zhou Y Z,Bi Q,et al..The mathematical model and properties of memristor with border constraint[J].Acta Physica Sinica,2010,59(9): 6673-6680.
[24]包伯成,王其红,许建平.基于忆阻元件的五阶混沌电路研究[J].电路与系统学报,2011,169(2): 66-70.Bao B C,Wang Q H,and Xu J P.On memristor based five-order chaotic circuit[J].Journal of Circuit and Systems,2011,169(2): 66-70.
