基于KPCA与随机森林的牵引电机局部 放电模式识别研究

王 卓，郑 祥，王仁峰，杨景杰，许智海

（大连交通大学 自动化与电气工程学院，辽宁 大连 116028）

0 引言

牵引电机定子绝缘介质在受到电、热等因素的影响时会发生老化，出现绝缘缺陷，导致定子发生局部放电（partial discharge，PD）[1,2]。

近些年，针对牵引电机的PD检测逐渐得到重视[3]。文献[4]为提高PD的检测灵敏度，通过在脉冲电压波形下检测到的PD起始电压，评估牵引电机的绝缘性能。文献[5]提出了一种基于可变上升时间的浪涌发生器测试方法，并将该方法用于检测绕线定子中是否发生PD。

上述PD检测方法的结果虽能够反映牵引电机整体绝缘状况，但无法据此确定具体故障原因，未能实现对PD类型识别。

通过牵引电机定子PD类型的识别，可以确定导致定子绝缘缺陷的具体原因；这对牵引电机的维护有重要意义。因此，本文针对牵引电机的PD类型识别做进一步研究。

不同类型的定子绝缘缺陷会表现出不同的PD模式，不同放电模式的放电信号具有不同的特征属性：可以通过这个特性对PD类型进行识别。

传统方法提取的PD信号特征维度过高，存在冗余特征，信号的重要特征信息不集中。文献[6]提取了PD信号的27个特征参数作为分类器的输入；但由于特征信息维度高，过多的无效信息导致识别结果不稳定。

针对特征维度过高、无效信息过多的问题，有学者提出了相应的降维算法。文献[7]在提取PD信号特征后，采用主成分分析（principal component analysis，PCA）算法对其进行特征降维，从而得到新的特征参数；这使得识别速度有了明显的提高。但是，降维处理后的传统特征对于PD的表征不明显，且PCA降维算法可能会使部分重要信息丢失，导致降维后的参数对于信号的分类效果不佳。

传统的PD信号识别算法有反向传播神经网络（backpropagation neural network，BPNN）、概率神经网络（probabilistic neural network，PNN）和支持向量机（support vector machines，SVM）等[8-10]。这些算法也因识别效果不佳逐渐被替代与改进。

文献[11]采用深度信念网络（deep belief networks，DBN）识别不同的典型PD类型，获得了较高的识别准确率；但DBN算法的结构比较复杂，训练的时间也比较慢，参数选择不当会导致陷入局部最优，使识别效果变差。

文献[12]采用遗传算法（genetic algorithm，GA）分别优化BPNN与PNN，并对PD信号进行了识别。虽然识别效果优于未改进算法，但改进之后的算法结构更加复杂，需要调节的参数增加，导致训练迭代的计算时间增加且迭代过程中易陷入极小值。

分形特征由于其区分能力强而在信号处理领域被广泛应用。将分形特征应用于牵引电机定子PD信号的特征提取，并与传统特征结合再进行降维，可以实现PD信号特点的更好表征，克服传统方法的不足。

随机森林算法是一个由决策树分类器组成的集成算法，能够较快地处理高维度数据且不易发生过度拟合，在模式识别领域有广泛的应用[13,14]。随机森林算法在PD模式识别中的应用较少。

基于上述分析，本文提出一种基于KPCA和随机森林的牵引电机定子PD信号模式识别方法。将分形特征与传统特征结合，以提高特征算法对PD信号的表征效果；采用KPCA算法代替常用的PCA特征降维算法，以深度挖掘特征信息，同时解决降维后易丢失重要信息的问题；采用随机森林算法进行PD类型识别，发挥其处理高维度数据速度较快且不易发生过度拟合的优势，提升识别效率。

1 算法原理

1.1 分形理论

分形理论提出，维数不一定是整数，可以分数的形式表示出，即分形维数[15,16]。

定义(F,D)为一个度量几何空间的数学模型，设R是F的非空紧集族，令B(f,ε)为一个球心为f、半径为正整数ε的封闭小圆球，将其视作一个小盒 子。设A⊂R2是一个非空集合，令N(A,ε)等于 覆盖A的最小盒子数，公式为：

式中：f1,f2,…,fM为F中的不同中心点。

进一步对非空集合A进行定义：

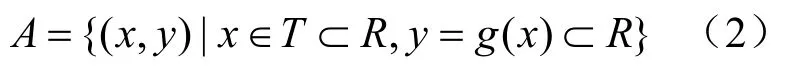
式中：g(x)为y对于X的映射函数，是一个连续函数。

计算分形维数：

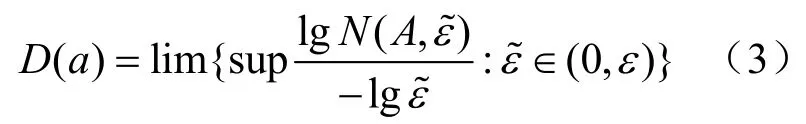
针对采样后的离散信号，对公式（3）进行简化。对接收的信号进行离散化采样后得s(t1),s(t2),···,s(tN+1)。对其进行分组，N取偶数，令：

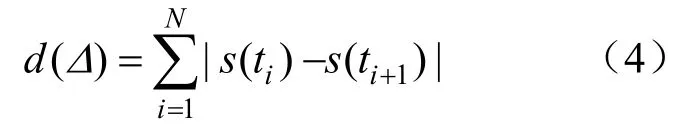
式中：(dΔ)表示N组相邻的采样点之间幅度绝对值差的和。随着采样点跳变程度的变大，()dΔ的值也会越大。

简化后的分形维数计算公式如下：

由公式（5）可知，分形维数反映了各组相邻离散采样点之间幅度跳变程度的相互关系；所以，分形维数可以作为一种特征参数，用以完成不同类型PD信号的识别。

1.2 KPCA算法

KPCA算法是一种非线性数据降维算法，可以用来去掉不重要信息，具体运算步骤如下[17,18]。

假设特征空间样本满足中心化，则特征空间F有协方差矩阵

引入n阶核矩阵K，其第i行j列的元素为。求解矩阵的特征值和特征向量，两边同时乘以φ(xi)，带入。令，得

求解该式得到特征值λ1,λ2,…,λn及对应的特征向量v1,v2,…,vn。前k个主成分所包含的信息 贡献率如下

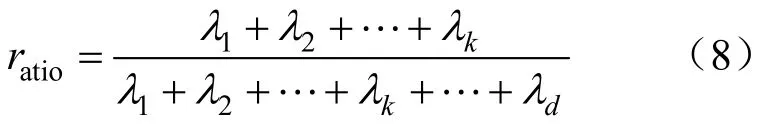
如果d维数据前k个特征值贡献率明显大于后d-k个特征值，则数据可以通过前k个特征向量来表达[19,20]。

本文采用KPCA算法进行降维处理，选择贡献率大于90%的前几个特征。

1.3 随机森林算法

随机森林（random forest，RF）算法：采用重抽样法，从N个训练样本集中随机抽取样本，重复N次组成一个与原训练样本数目相同的新训练集。新训练集中的每个样本被选中的概率均为1/N。这样重复k次。将训练集分成k个新训练集，对新训练集进行建模得到对应k个互不相关的模型。以此模型为基础构成k个决策树，形成森林。通过每个模型对样本各决策树投票，哪一类得票多即归为哪一类[21,22]。

RF算法可以有效解决过拟合和决策树准确性不高的问题，其优点是实现方式简单、分类准确度高且分类速度快。算法训练步骤如下[23]。

步骤1：通过重抽样方法，从原始样本集中随机选取k个训练样本集和k个袋外数据集。袋外数据集对应的决策树会对样本进行投票得到预测结果，于是分类错误样本占总样本的比率就是袋外误差。可以直接使用袋外误差对其进行泛化性评估。

步骤2：从特征参数中随机选取最优特征，作为决策树节点分裂的分裂属性节点。

步骤3：用训练集和抽取的特征子集训练决策树。k个训练样本集分别得到k颗决策树。

步骤4：将每颗决策树的输出结果线性集成，最终得到RF算法整体的输出。最终的分类决策输出为

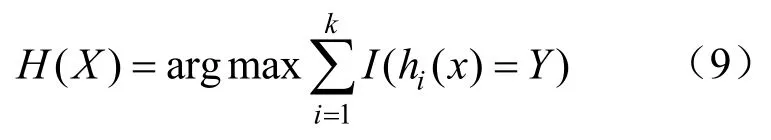
式中：H(X)为组合分类模型；hi(x)为单个决策树分类模型；Y为输出变量；I(·)为指示函数。

2 信号预处理

为了验证本文方法的实用性，对牵引电机定子PD的表面放电、内部放电、自由放电共3类特高频故障信号进行处理。

采样频率为2 GHz。每个PD信号含10 000个采样点。对应信号波形如图1所示。

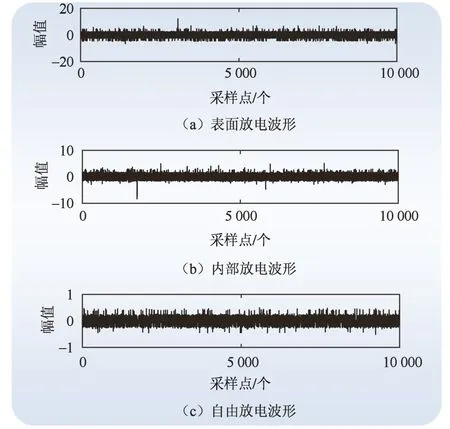
图1 PD信号波形 Fig. 1 PD signal waveform

采用连续自适应小波软阈值去噪法进行去噪处理。去噪后的信号波形如图2所示。由图2可以看出，PD信号已被有效分离出来。

图2 PD信号去噪波形 Fig. 2 PD signal denoising waveform

3 算法性能测试

3.1 基于分形维数的特征提取

通过集合经验模态分解，将PD信号分解为各个固有模态分量（intrinsic mode function，IMF），进而得到各个频段的信号的特性。

自由放电去噪信号经分解后，其波形如图3、图4所示。在信号分解后，进一步对IMF进行分形维数的计算，计算结果如图5所示。

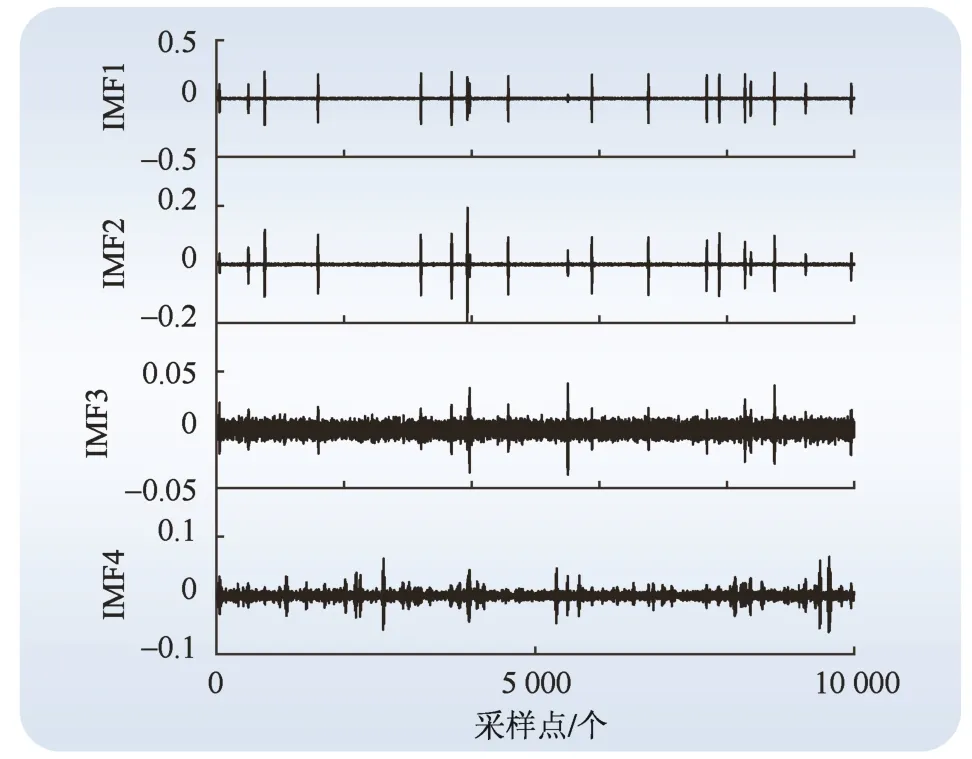
图3 自由放电信号分解波形（IMF1—IMF4） Fig. 3 Free discharge signal decomposition waveform (IMF1—IMF4)

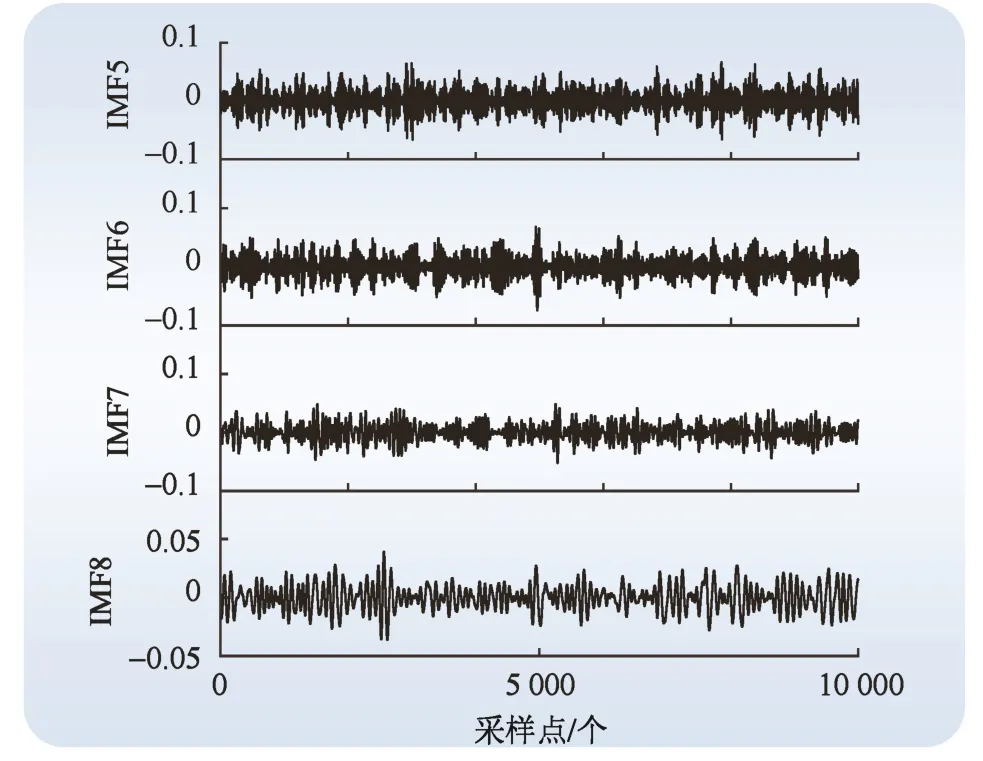
图4 自由放电信号分解波形（IMF5—IMF8） Fig. 4 Free discharge signal decomposition waveform (IMF5—IMF8)

图5 不同PD信号的分形维数 Fig. 5 Fractal dimension of different PD signals

从图5可以看出，不同类型的PD信号在各个IMF阶次的分形维数存在着明显不同，因此可以把PD信号在各个IMF上的分形维数作为模式识别的特征参数。

3.2 特征降维

针对传统PD特征对信号表征不明显的问题，将分形特征与传统的时频域特征结合，使特征能够从不同角度刻画PD信号的状态。这些特征的名称如表1所示。

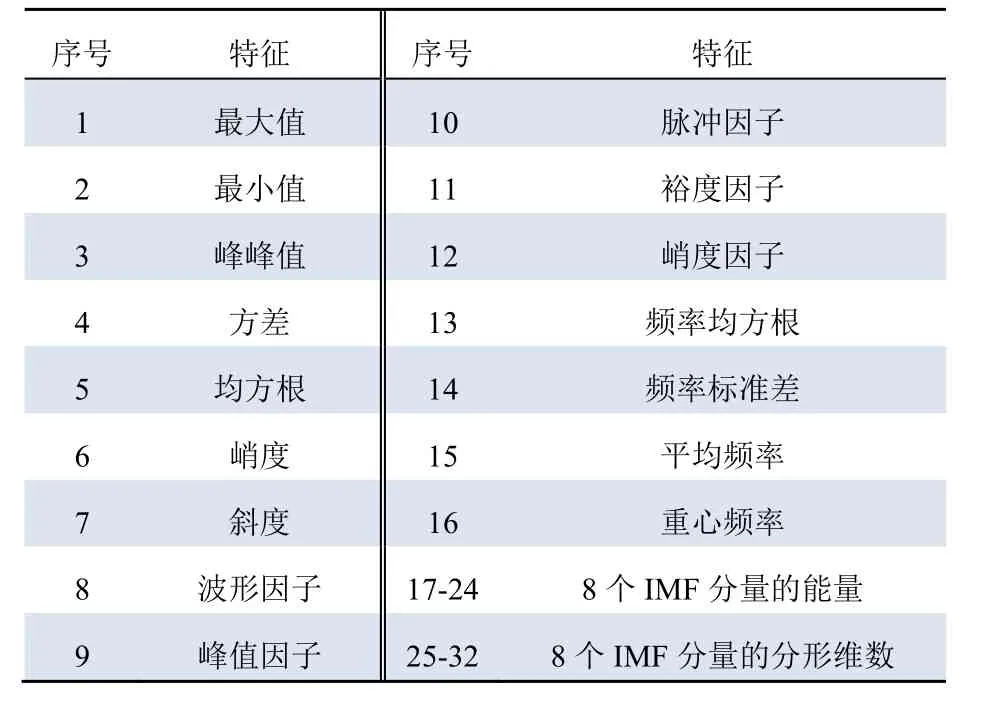
表1 特征参数名称 Tab. 1 Feature parameter name

表1中，序号为1—12的参数为时域特征参数，13—16为频域特征参数，17—24为时频域特征参数，25—32为分形维数。

加入分形特征之后，数据特征维度会过高，这将导致识别速度慢；因此，有必要对特征集进行数据挖掘降维。

由于PD信号的特征很难满足线性关系，故采用KPCA降维——将非线性信号特征投影到高维空间，使其线性可分。

降维后的核主成分贡献率越大，所含PD信息越相关。本文将贡献率大于90%的前k个主特征作为分类器的输入特征。

核主成分特征贡献占比如图6所示。从图6中可见，第1个核主成分的贡献率占总贡献率的45%左右，第2个核主成分的贡献率占总贡献率的15%左右，其中贡累计献率超过90%的核主成分为前9个；因此，本文选择前9个核主成分作为输入特征。

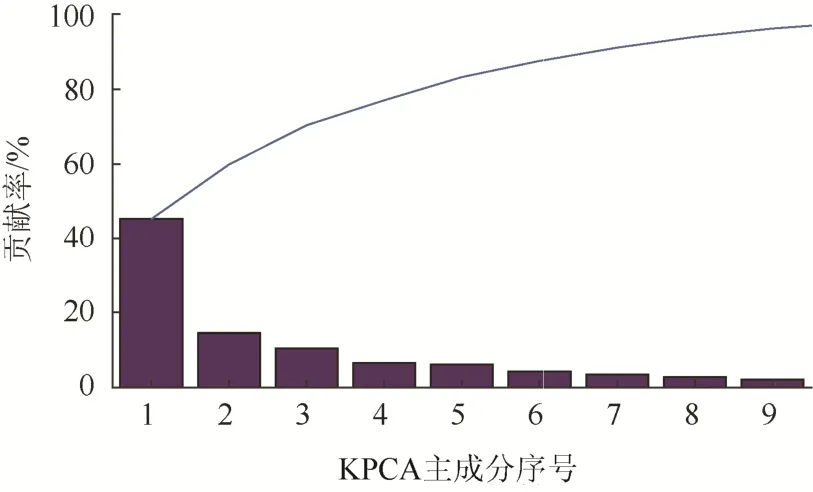
图6 主成分贡献率 Fig. 6 Principal component contribution rate

3.3 RF算法分类

本文采用RF算法建立PD分类模型。首先，随机选取450个样本作为训练样本进行训练。训练结束后，用剩余的150个样本测试PD模式识别的准确性。

RF分类器性能分析如图7所示：空间中央正方体部分为识别模糊区域，很难归类；靠近端点处划分明显。

图7 RF分类器性能分析 Fig. 7 RF classifier performance analysis

经过计算，随机森林算法对不同类型牵引电机定子PD类型的识别准确率均在90%以上。

为了验证RF算法的优势，选取遗传算法优化的反向传播神经网络（GA-BP）、遗传算法优化的概率神经网络（GA-PNN）和DBN算法与RF算法进行比较。分别输入传统特征（TR）与结合分形特征的降维特征（FR）进行PD信号分类测试。

10次实验识别结果如图8、图9、表2所示。

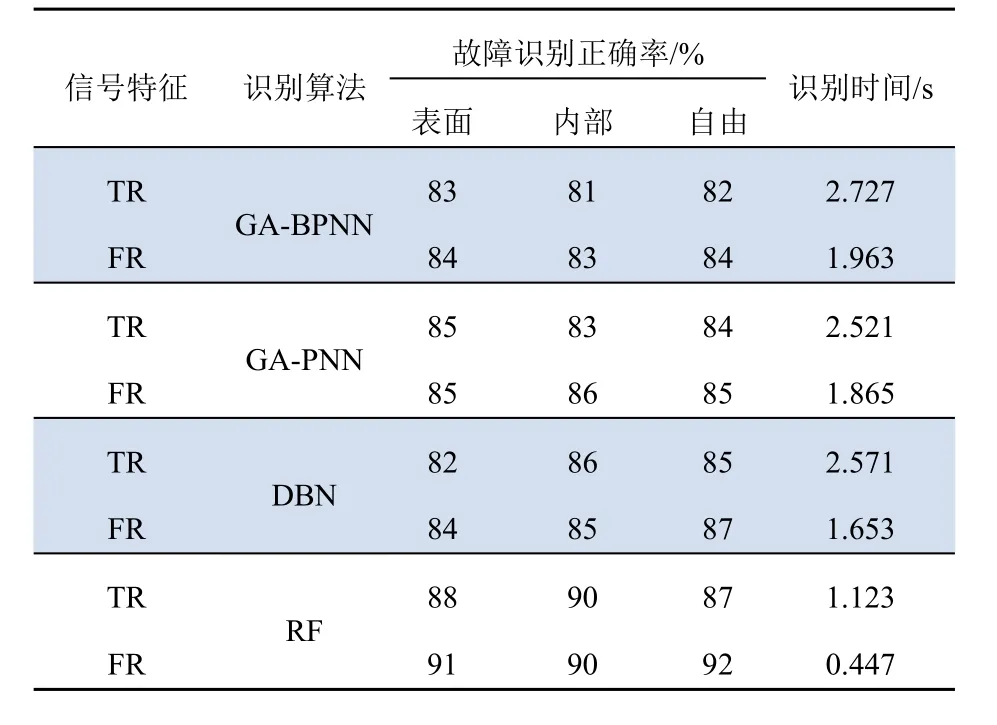
表2 模式识别结果对比 Tab. 2 Pattern recognition results comparison

由图8和图9所示的识别准确率曲线可以看出，相较于其他方法，FR特征和RF算法结合的牵引电机定子PD模式识别方法的识别结果更加准确，其准确率稳定在90%以上。

图8 基于分形降维特征的算法识别 Fig. 8 Algorithm recognition based on fractal dimension features

图9 基于传统的统计参数信号特征的算法识别 Fig. 9 Algorithm recognition based on traditional statistical parameter signal features

同时，在多次测试中，随机森林算法比其他算法的识别过程更加稳定。

由表2可以得出：采用分形特征与传统特征结合进行KPCA降维，可以缩减PD模式识别所需时间。

4 结论

本文提出了一种基于KPCA和RF的牵引电机定子PD模式识别方法：将牵引电机PD信号的分形特征与传统特征结合，采用KPCA算法进行降维处理，通过RF算法进行PD类型识别。

（1）将传统特征与分形特征融合，可以更好地表征不同类型PD信号的特点。

（2）与普通降维算法相比，KPCA算法不仅减少了特征参数的数目且更好地保留了PD信号的特征信息，缩减了PD模式识别的时间。

（3）相比于其他的识别算法，RF算法在识别过程中准确率与识别稳定性有显著的提高：识别准确率均在90%以上，识别时间均在0.5 s以下。

综上所述，本文所提方法明显优于传统特征参数和其他常用识别算法。