十二相4Y移15°绕组同步发电机三相交叉 对接不对称突然短路电流分析

孙俊忠，周智勇，王宗亮，孙 硕

（海军潜艇学院 动力系，山东 青岛 266071）

0 引言

多相电机带整流桥可以提供高品质的直流电能，其应用越来越广泛[1-3]。十二相4Y移15°绕组同步发电机带整流桥是目前应用广泛的多相发电机整流供电系统[4,5]。该系统不仅在整流桥故障的情况下会发生不对称短路，而且在带整流负载的正常运行中，也会处于不对称运行状态[6]。例如，当十二相4Y移15°绕组同步发电机各自的三相整流桥并联时，由于换相电抗的影响，电机出现换相重叠，可能会出现二阀导通—四阀导通—二阀导通的状态。此时的四阀导通即相当于两相—两相不对称短路运行。如果此时直流侧发生短路，则相当于发生四相不对称短路。不对称突然短路是该类电机的一种重要故障工况，分析其动态过程、得到此时的电流、磁链、电压和转矩的表达式及各种极限参数（最大冲击电流、转矩等），对于该类电机的合理设计和可靠运行具有重要意义。

文献[7,8]建立了六相（3/3）双绕组电机的数学模型，并根据谐波平衡原理[9]分析了2套不同绕组之间的两相——两相不对称突然短路。相比于2套不同绕组之间的不对称短路，十二相整流绕组内部更易发生各种短路故障，所以分析十二相整流绕组之间的不对称短路意义更大。本文在文献[7,8]的基础上，通过适当近似简化，给出相对简单的适合不对称突然短路分析的十二相电机数学模型，以两Y绕组之间三相—三相交叉对接短路（简称三相交叉对接短路）为例进行突然短路电路电流的分析，得出了该不对称突然短路工况下的短路电流完整表达式，通过近似简化给出了适合工程应用的最大短路电流的估算公式，并通过试验检验了模型和分析方法的准确性。

多相电机的电磁关系比较复杂，解析分析难度较大，研究其性能采用仿真方法普遍，例如文献[10-12]等。与仿真法比较，解析法更易得到规律性认识，更方便工程应用。譬如，问献[13]建立了十二相发电机整流系统的等效三相模型，并推导出了直流极间短路时短路电流的解析表达式。应用本文建立的简化数学模型，可以对十二相电机的各种过渡过程进行解析分析，便于研究十二相电机的性能。

1 数学模型

十二相4Y移15°绕组同步发电机定子相轴和转子轴线相对位置如图1所示。根据文献[8]，可得到αβ0坐标系统的基本磁链和电压方程（因为不引出中线，所以不考虑零轴分量）：

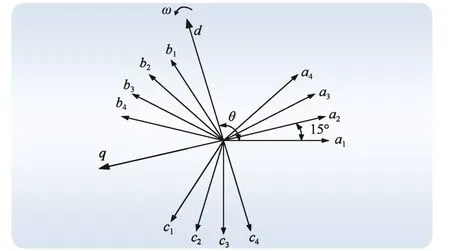
图1 定子相轴和转子轴线相对位置 Fig. 1 The relative position between the axis of stator and rotor windings

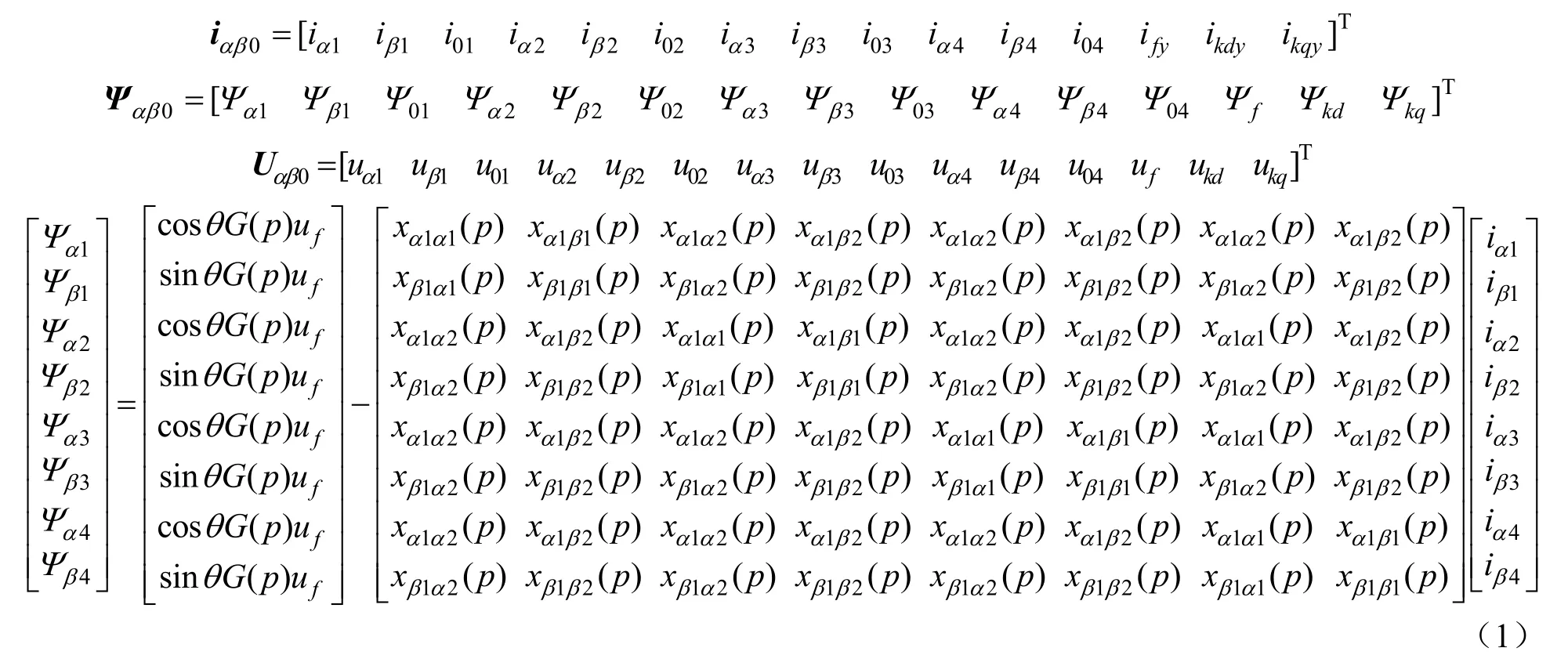
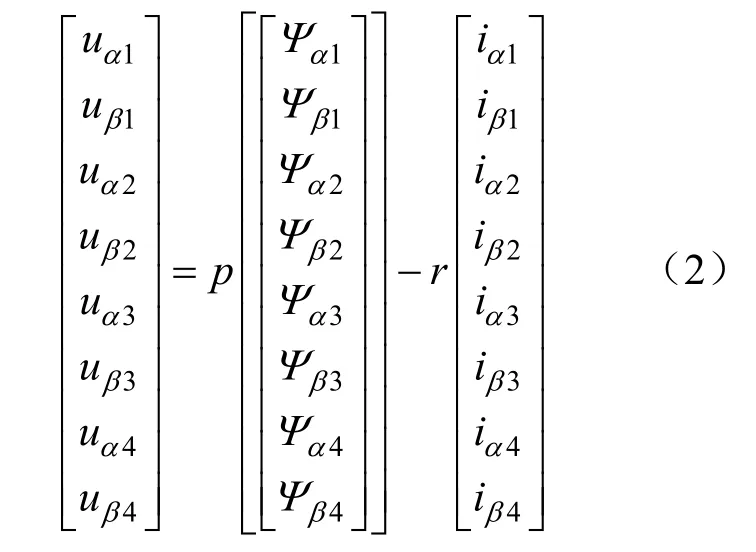
式中：

xsy、xsm分别是各绕组自漏抗和互漏抗，均为常数。其他参数的意义，参见文献[8]。

2 不对称突然短路分析方法

一方面，根据磁链守恒原理，同步电机在突然不对称短路瞬间，为保持各闭合回路磁链不发生突变，在定子闭合回路中要产生相应的非周期分量。所产生的空间静止磁场，在转子绕组中感应出基频电流。由于转子的不对称，这个基频电流的磁场会在不对称的定子回路中感应出二次谐波分量；如此反复作用，在定子绕组中产生一系列偶次谐波分量，在转子绕组中产生一系列奇次谐波分量。同理，由于转子绕组中的非周期电流的存在，定、转子中将分别产生一系列奇、偶次谐波分量。因此，在突然非对称短路的过渡过程中，短路电流含有非周期分量和各次谐波分量，所以可令：

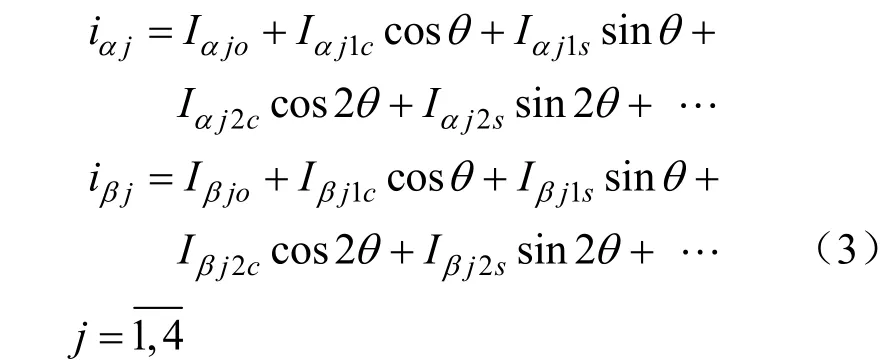
式中：j=1,2,3,4；Iαjo,Iβjo是非周期分量；Iαj1c，Iβj1c，Iαj1s，Iβj1s，…为相应的各次谐波分量的 余弦部分和正弦部分的幅值，均为时间的指数衰减函数。

另一方面，根据磁链和电压方程以及三相交叉不对称短路的端点条件，应用叠加原理，在忽略定、转子回路对交变电流电阻的条件下，可解出短路电流的另一表达式。以上2式表示的是同一电流。根据谐波平衡原理[14]，其对应项的系数应相等；由此可得到相应的包含微分算子p的代数方程，即相当于把时变系数的微分方程转化为简单的代数方程。解这些代数方程，并应用海氏展开定理，可以得到十二相四Y移15°绕组同步发电机突然三相交叉不对称短路电流各次谐波的幅值和相应的时间常数，从而可直接得出其短路电流的完整表达式。

3 磁链方程的简化

为了进一步简化模型，方便后面的不对称突然短路分析，采取与三相电机过渡过程分析类似的简化方法，进一步简化磁链方程。

忽略定子回路对交变电流的电阻，将（3）式代入（2）式可得：

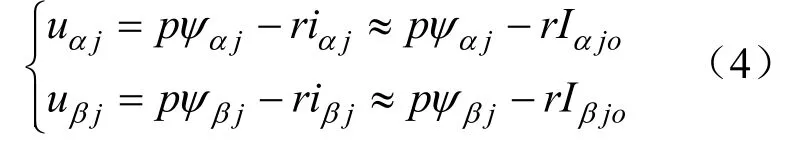
忽略转子回路对交变电流的电阻，即取：

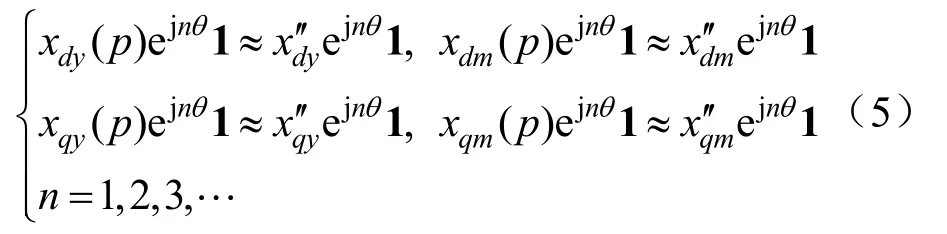
将（5）式代入（1）式后，可得到简化的磁链方程如下：

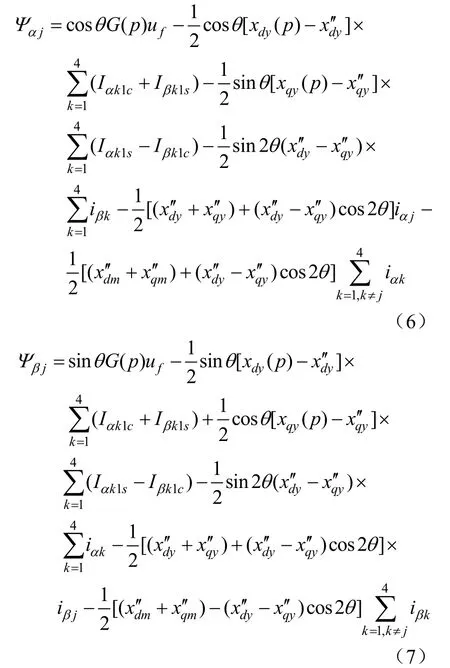
4 三相交叉对接突然不对称短路电流分析

为分析方便，假定Y1分别与另外3个Yj(j=2,3,4)发生三相交叉对接突然不对称短路。以Y1和Y2差15°三相交叉对接突然不对称短路为例，表示此时的短路情况，如图2所示。假设短路后励磁不 加调节（Δuf=0）、转速保持额定转速不变（ω=1）。

规定：以a1相轴线为标准，另一Y中与a1相相接的相的轴线超前a1相轴线的角度为α（即差α角，图2所示）。α角为正表示a1相轴线落后于另一与之对接短路相的轴线；反之，则表示a1相轴线超前于另一与之对接短路相的轴线。

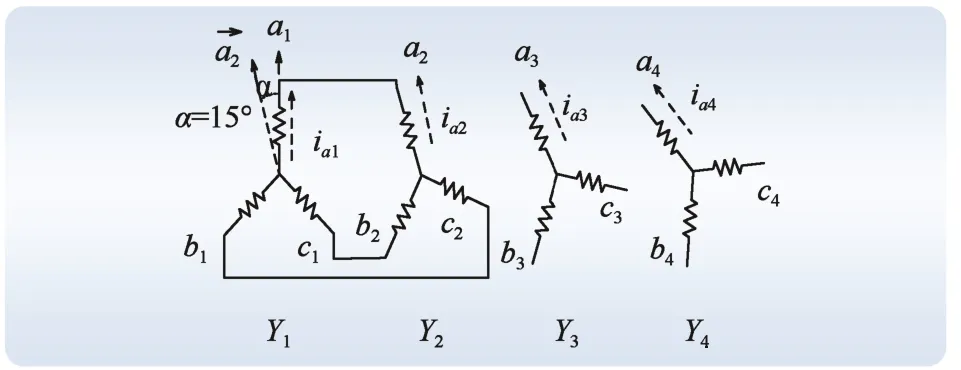
图2 差15°三相交叉对接突然不对称短路 Fig. 2 Three-phase-cross-connection sudden unbalanced short circuits by 15°

经分析，三相交叉对接突然不对称短路共有9种不同的情况（见表1）。

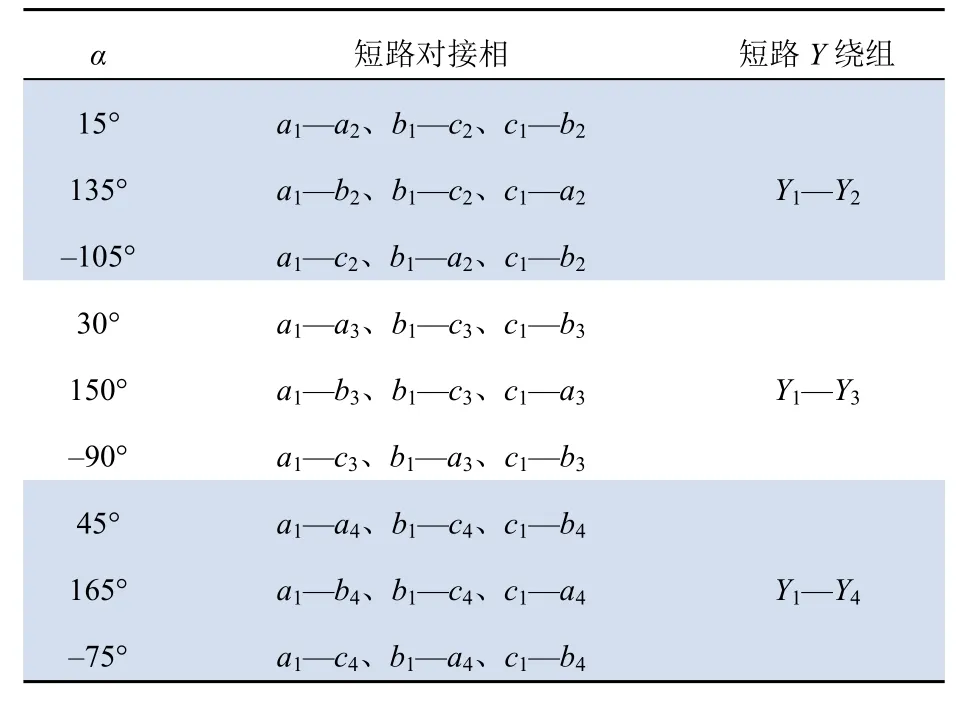
表1 三相交叉对接突然不对称短路 Tab. 1 Three-phase-cross-connection sudden unbalanced short circuits

4.1 统一的端点条件

三相交叉对接突然不对称短路共有9种不同的情况，一一分析将十分繁杂。为此，本文通过归纳，总结出统一的端点条件，一次性分析，就可以得到全部9种不同的短路电流表达式，极大简化了分析过程。

以差15°三相交叉对接突然不对称短路为例，如图2所示，可写出abc坐标系下的端点条件：

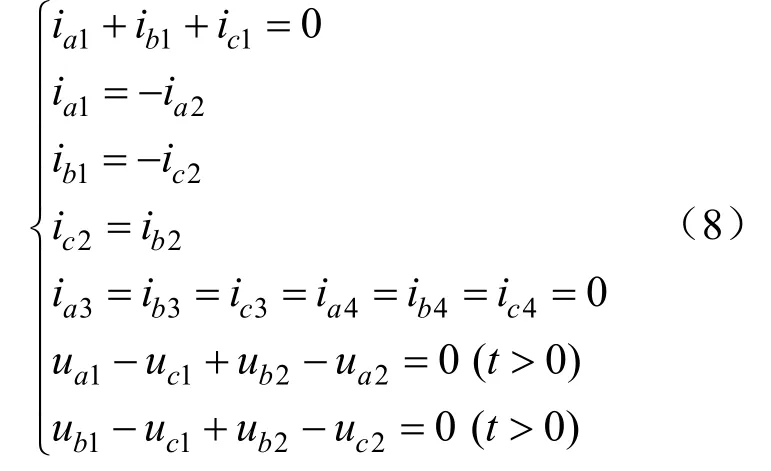
将上面的端点条件变换为αβ0坐标系下的端点条件，根据叠加原理，突然短路可以看作是突然加上一个与原来相反的电压，可得如下端点条件：

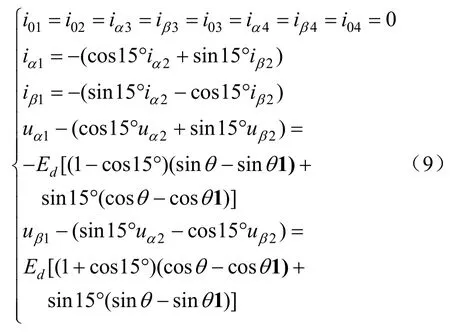
式中：黑体“1”表示单位阶跃函数。

其余8种不同短路情况的端点条件也可类似写出，归纳它们的共同特点，可得到统一性的端点条件如下：

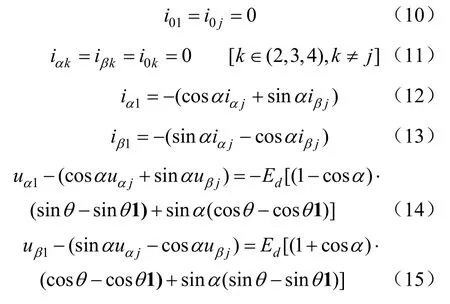
式中：j=2，3，4。

为了方便后面的解析分析，对上述统一的端点条件进一步简化。

由式（12）（13）可得：

或

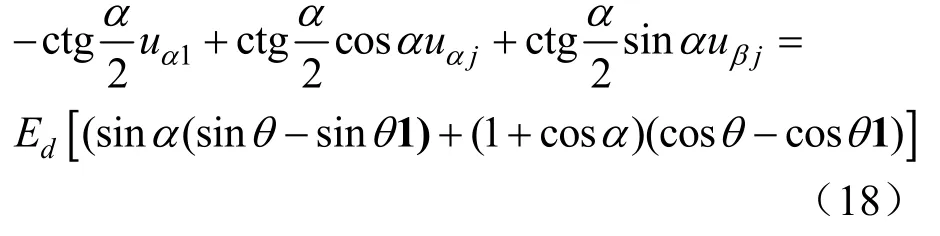
比较式（18）和式（15），可得：

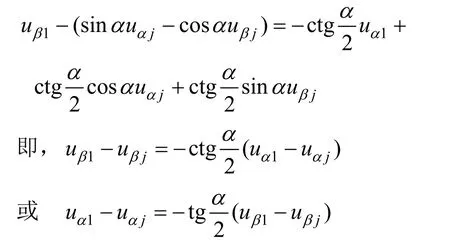
将电压方程式（2）和磁链方程式（1）代入上式，得：

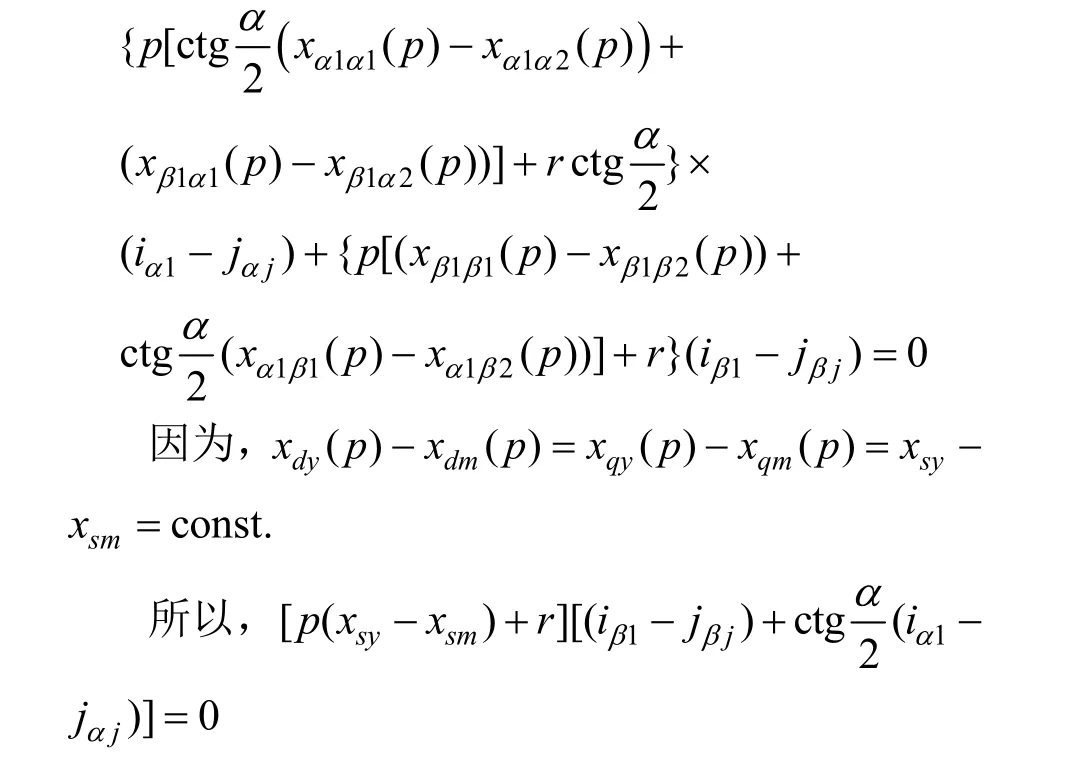
故可得：

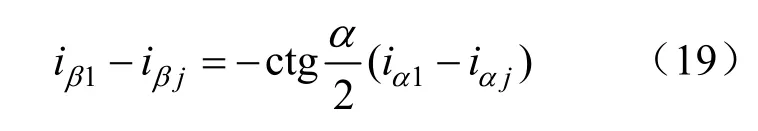
或

比较式（19）（20）与式（16）（17），可得

由此，根据磁链方程式（1）和电压方程式（2），可得，

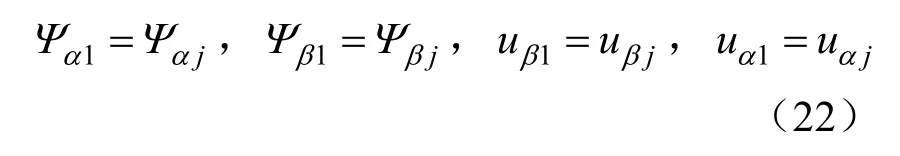
由式（12）（13）（21）可得，

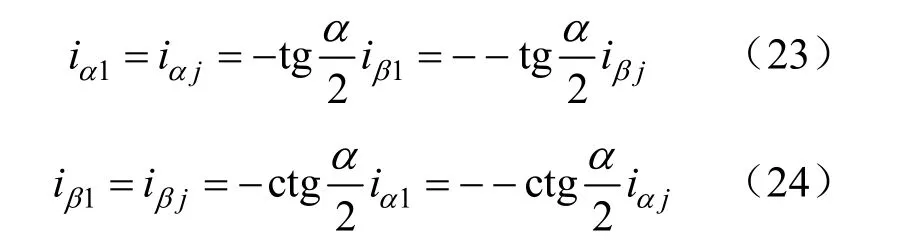
综合上面的分析，可得简化的统一端点条件如下：

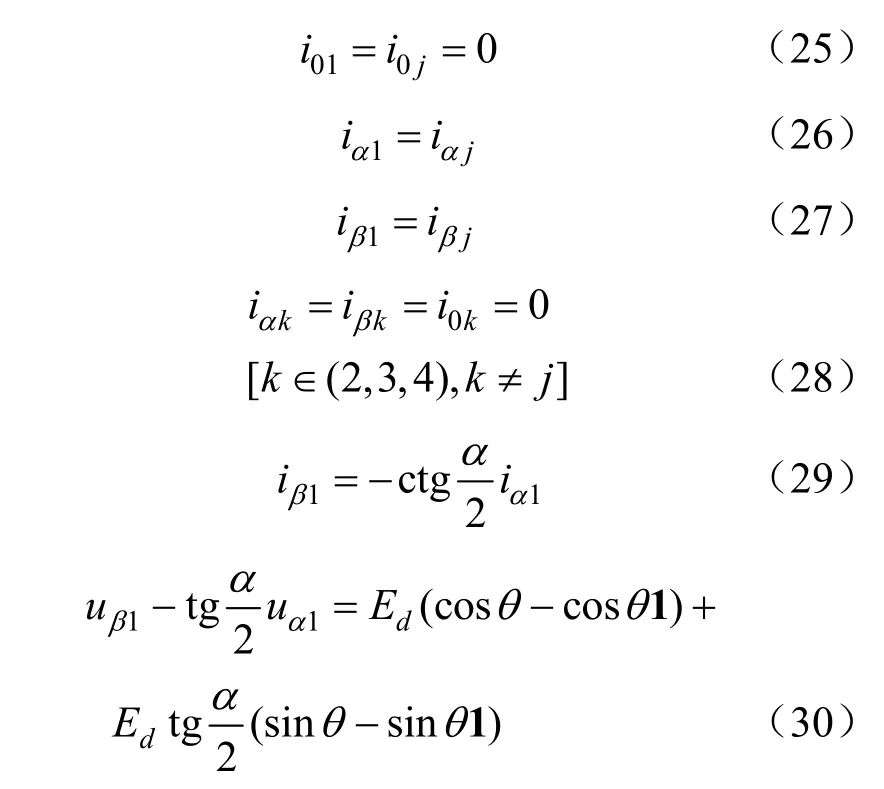
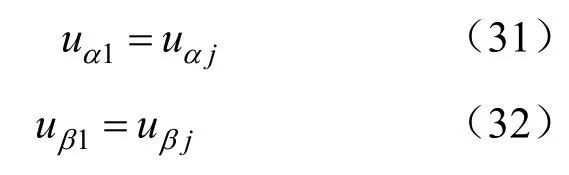
式中：j=2，3，4。

4.2 短路电流分析

将电压方程式（2）代入式（30），可得：

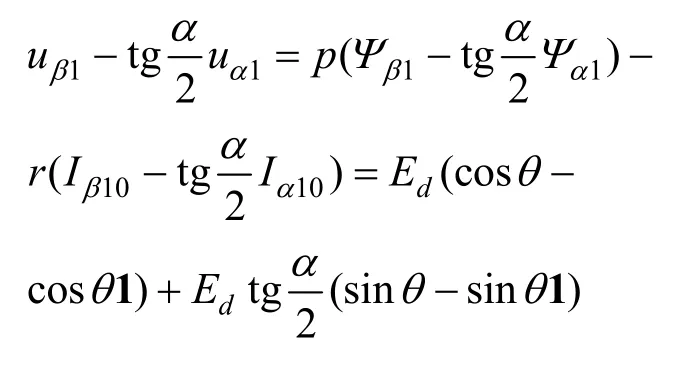
所以，

另一方面，由简化的磁链方程和端点条件，还可以得到：

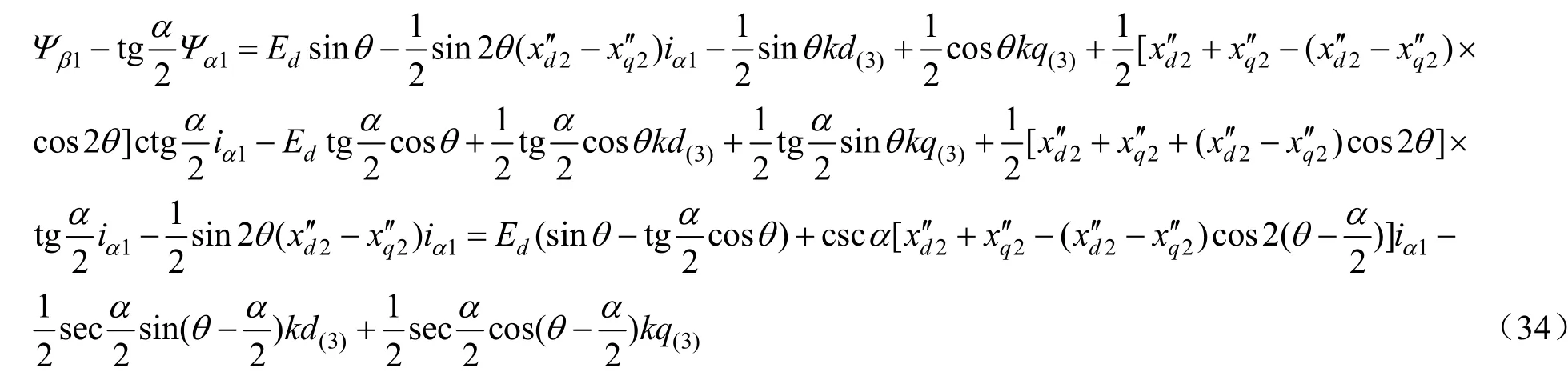
式中：

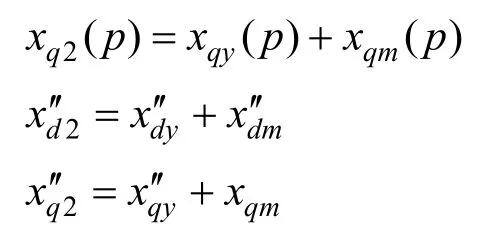
由式（33）、式（34）相等于，得

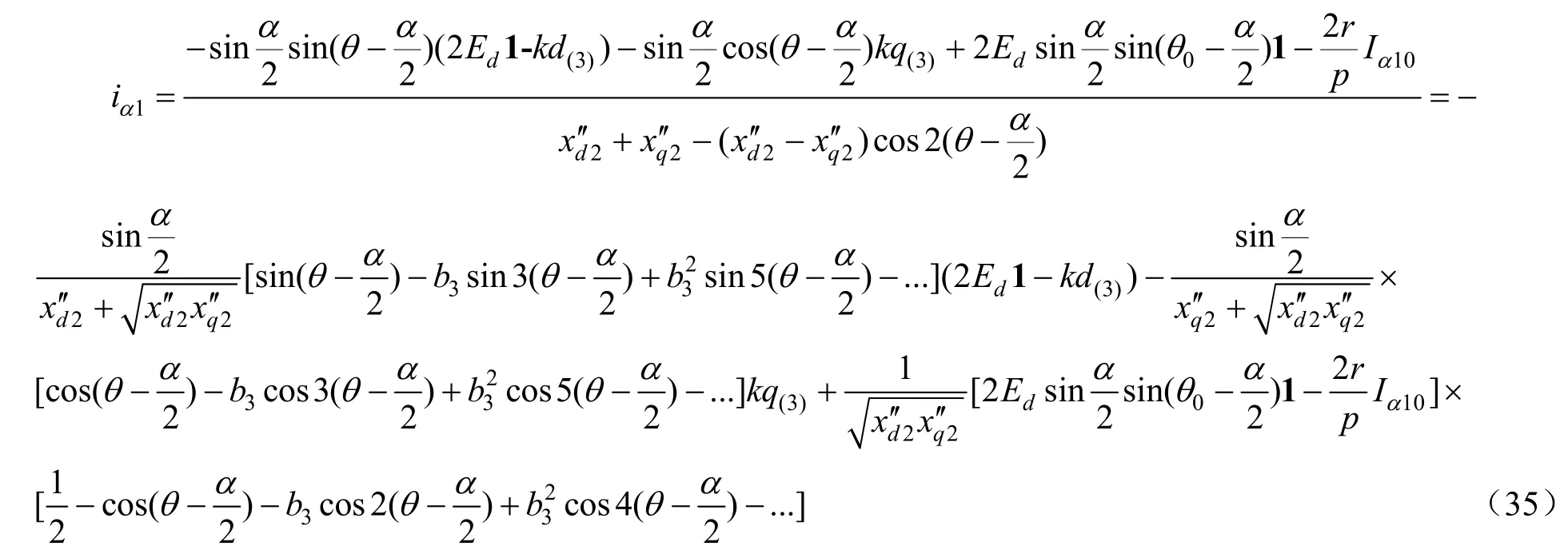
根据前面的分析，三相交叉对接突然不对称短路后的电流可表示为：

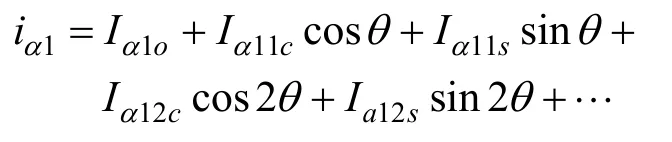
经过变换可得：

比较式（35）和式（36），根据谐波平衡原理，其对应项的系数应相等，即

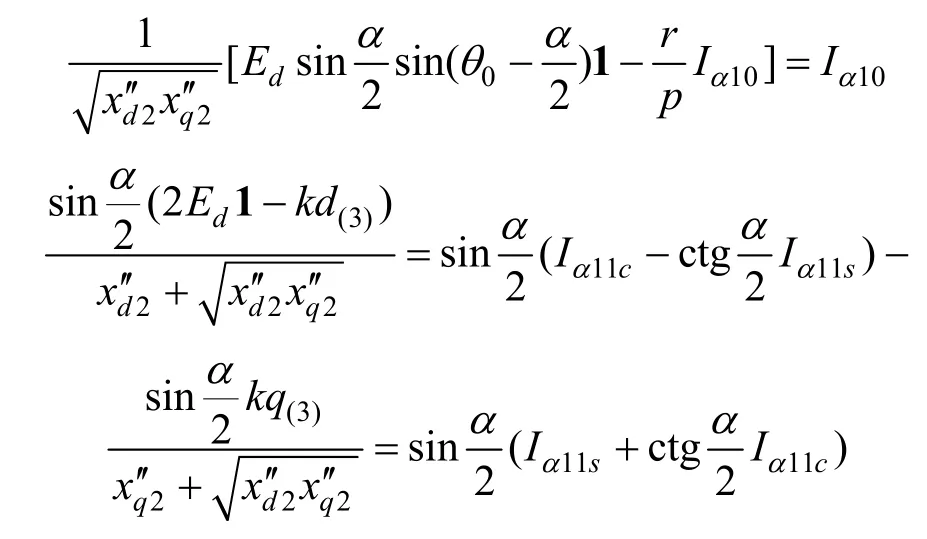
由此可得到相应的包含微分算子p的代数方程，即相当于把时变系数的微分方程转化简单的代数方程。解这些代数方程，并应用海氏展开定理，可得：

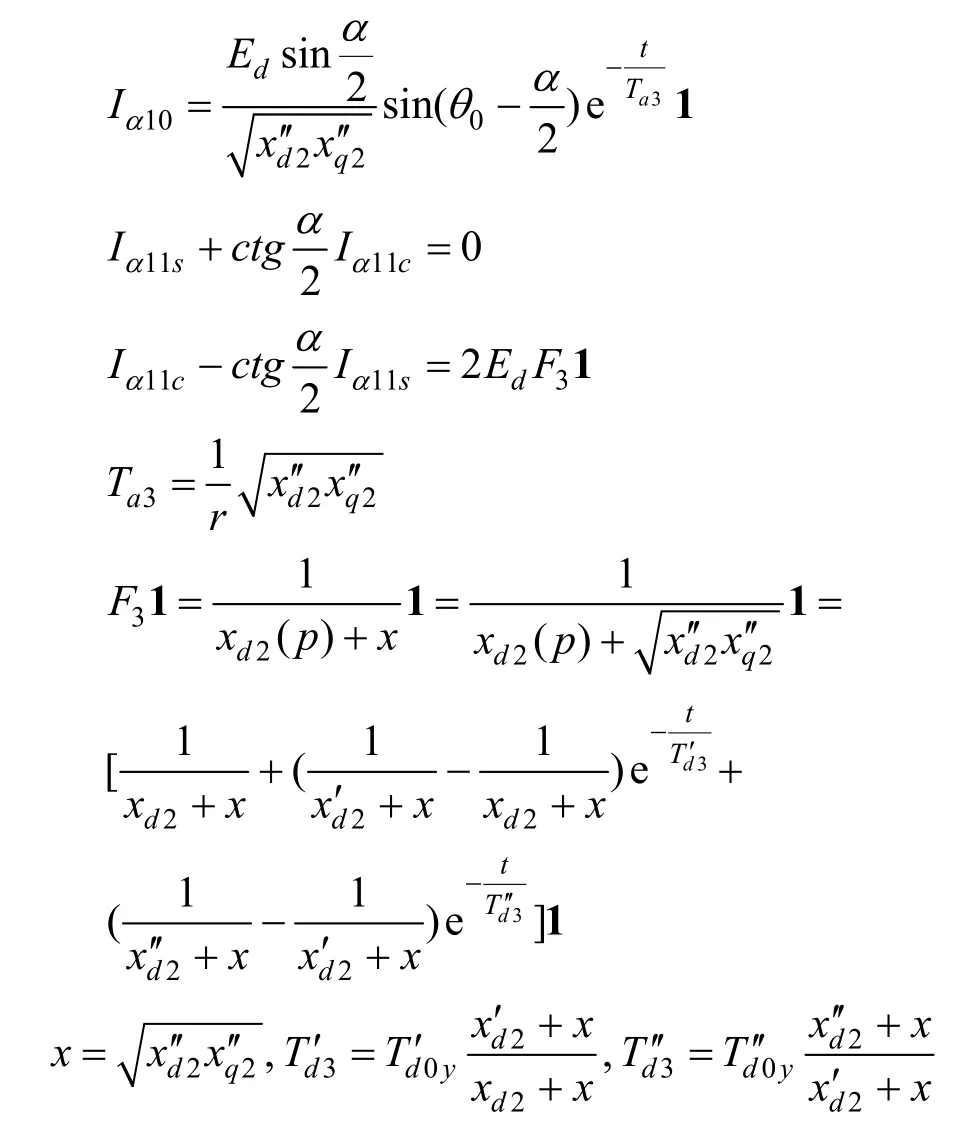
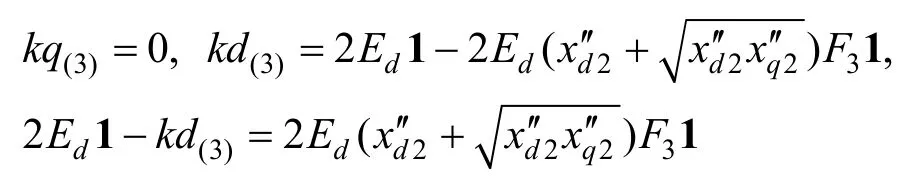
将上面解得的结果代入（35），则得：

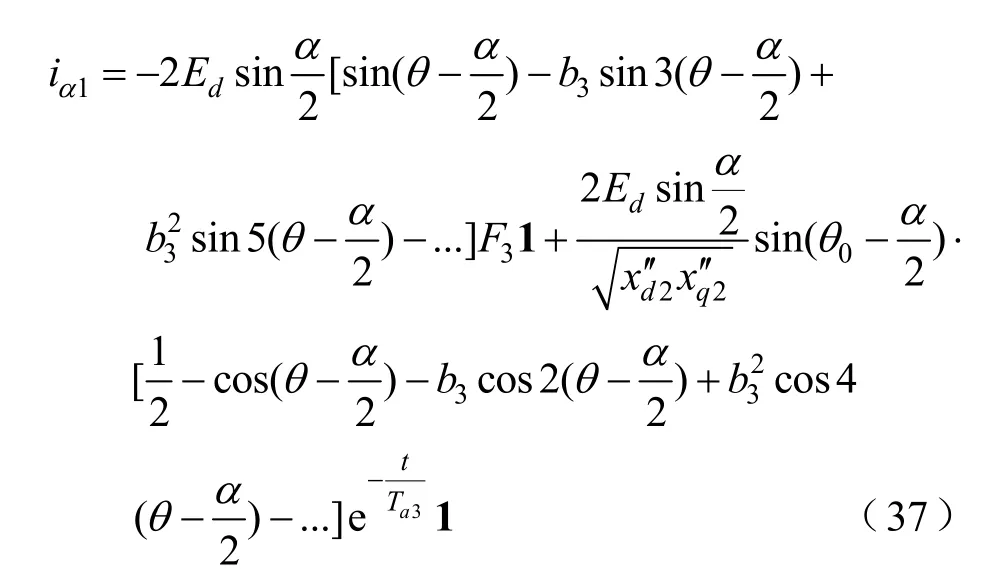
所以可得：

与Y1对接的另一个Y的三相短路电流分别等于与之相接的Y1相应相电流，到此就得到了三相交叉对接突然不对称短路电流的完整表达式。

4.3 最大冲击电流

上面虽然得到了短路电流的表达式，但其还是比较复杂。突然短路后，主要关心的是最大短路电流（冲击电流）及其到达的时刻。为了得到更适合工程应用的简明的最大短路电流表达式，参照三相电机突然短路最大电流的近似分析方法，忽略短路电流的衰减[14-15]，可得：

据此可分别得出各种短路的最大冲击电流，如表2所示。

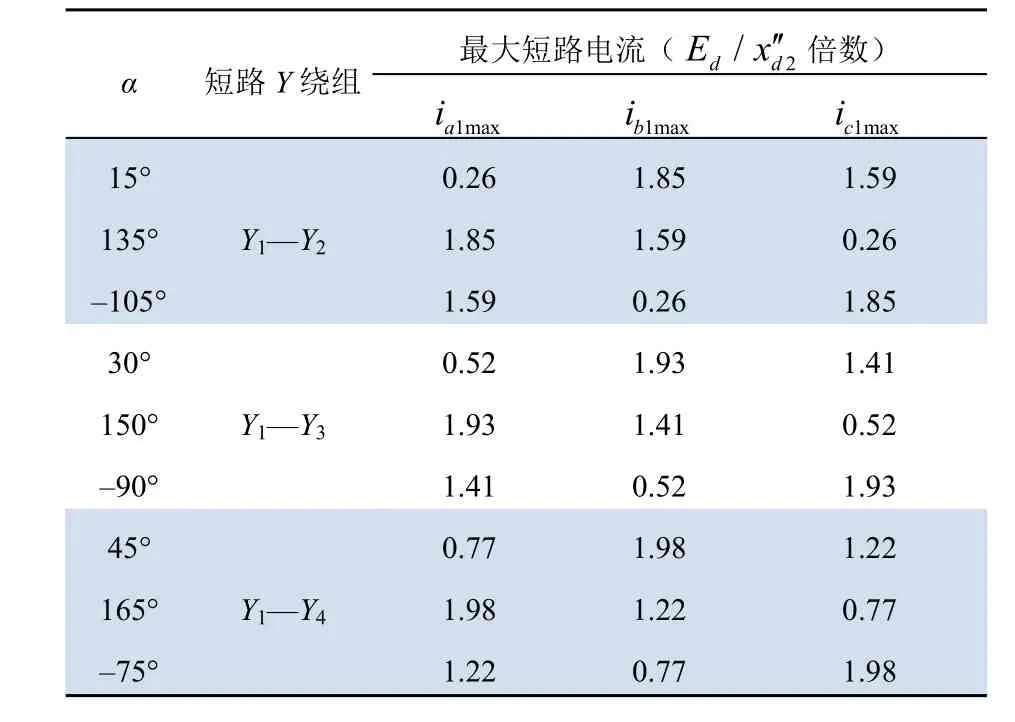
表2 三相交叉对接突然不对称短路最大冲击电流 Tab. 2 The maximum impact current of three-phase- cross-connection sudden unbalanced short circuits

比较可知，在Y1与Y4对接短路时，冲击电流最大；而α=45°时，

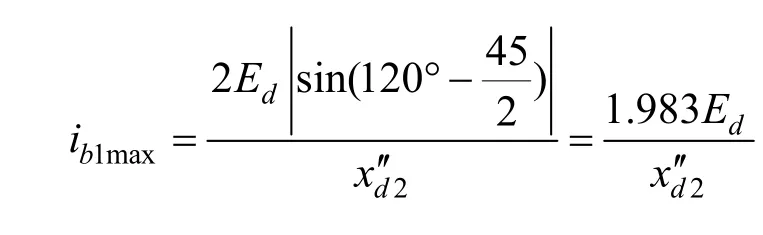
5 试验验证

试验电机为3/12相双绕组电机，整流绕组为十二相4Y移15°绕组同步发电机。试验电机额定值如下。

取Y1—Y43种三相不对称短路为例进行试验和计算，最大短路电流实测波形如图3所示，计算结果见表3。

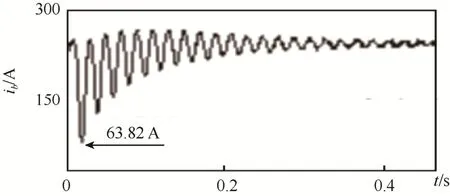
图3 最大短路电流实测波形 Fig. 3 The experimental waveform of the maximum short-circuit current

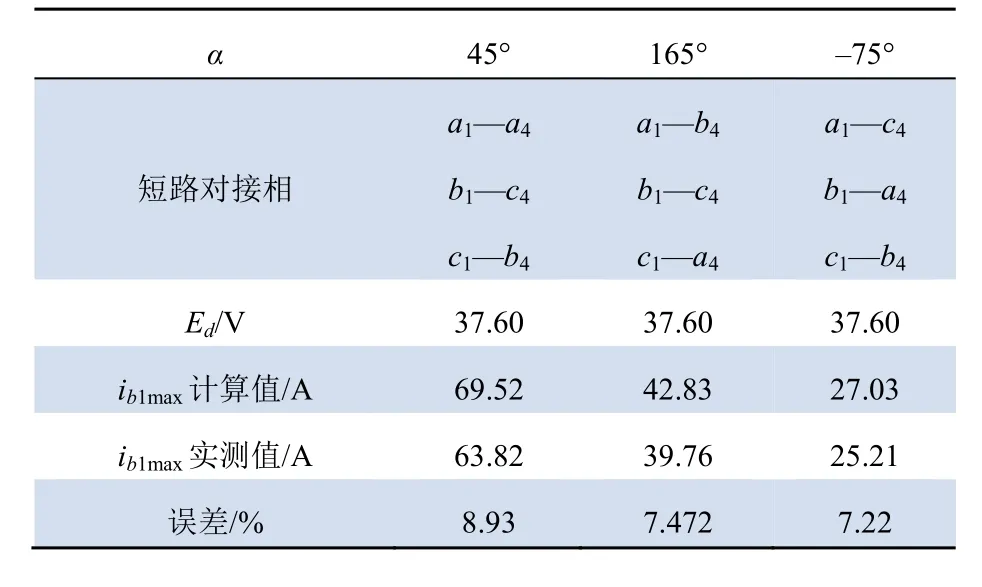
表3 计算和实测的短路电流最大值对比 Tab. 3 The comparison between calculated and experimental maximum short-circuit currents

由表3可知．计算值和测量值的误差在10% 以内，符合工程要求；这说明本文的解析分析方法是正确的。

6 结论

本文根据谐波平衡原理，采用解析分析方法，分析了十二相4Y移15°绕组同步发电机三相对接不对称短路，得到了短路电流的完整解析表达式和最大短路电流的近似估算值。谐波平衡原理分析电机的不对称突然短路，物理概念清晰，逻辑性强，方便易行，可用于分析其他的各种不对称短路。理论分析结果与试验结果吻合的较好，说明本文的分析方法是可行的。