基于电价敏感度和价格弹性的地区需求响应潜力评估

欧 飞，刘 敏，李 震

（1. 贵州大学 电气工程学院，贵州 贵阳 550025； 2. 贵州电网有限责任公司 电网规划研究中心，贵州 贵阳 550002）

0 引言

在实现“碳达峰”和“碳中和”重要任务[1]的背景下，传统的火力发电量面临削减。同时，新能源发电和需求响应策略成为保证电力系统安全稳定运行和电力可靠供应的重要举措[2]。

电力系统需求侧的可控负荷，如空调、热水器和电动汽车等，蕴含巨大的电能调节潜力[3]。电力公司可以通过价格和激励等措施，引导需求侧资源改变自身用电模式，帮助电网实现削峰填谷、消纳新能源的运行目标[4]。同时，通信技术和物联网技术的快速发展，也为需求响应的实现打下了基础[5,6]。

各地实时电价和激励政策的发布，需要以该地区参与需求响应的潜力为基础，且电力系统的优化调度也需要考虑需求响应的潜力；因此，对地区进行需求响应潜力评估，可以为电力公司制定需求响应策略提供有力帮助。

在需求响应潜力评估方面：

文献[7]利用非侵入式负荷监测和聚类算法分析了用户的用电行为，进而评估了用户的需求响应潜力；但文中只评估了用户的需求响应潜力。

文献[8]利用非侵入式负荷识别技术识别出用户的可中断负荷，提出由下至上的台区负荷需求响应能力在线聚合监测方法；由于这种方法在应用时需要对每个电力用户进行非侵入式负荷识别，再将每个用户的响应能力进行聚合，所以存在计算量庞大、聚合误差高的问题。

文献[9]从需求响应能力和速度2个评价指标出发，运用需求价格弹性矩阵，评价了居民小区参与需求响应的潜力。

文献[10,11]分别聚焦于温控负荷和电动汽车的响应潜力，针对单一类型的负荷进行了分析。

本文从变电站供电区域角度出发，提出需求响应潜力评估方法。与现有方法相比，本文所提方法的创新性体现在：（1）直接利用区域用电量和电价，从宏观层面进行地区需求响应潜力评估；（2）提出电价敏感度概念，据此筛选出需求响应潜力高的地区；（3）提出分级弹性系数概念，用于精确计算地区响应电量。

1 电价敏感度

响应潜力评估的本质，是量化电力特征信息（如电价、用电量等）与响应标签（用户响应信息）之间的关系。响应标签通常是匮乏的[12]。电价作为电力市场的杠杆，能够有效引导用户的用电行为[13]。根据电量随电价的变化趋势，可判断用户是否对电价变化做出了反应。

需求响应潜力评估的研究主要集中在响应速度和响应能力上。用户是否参与需求响应是一个不确定的事件，即电价上升后用户不一定会减少用电量；所以，本文提出电价敏感度概念，据此评价用户参与需求响应意愿的强弱。

将某区域一天的电价与电量数据[14]经式（1）标准化处理，结果图1所示。从图1中可以看出，当电价陡然上升时，用电量上升趋势放缓或者开始减少；这表明，该地区的用户对电价变化敏感，参与需求响应的意愿较强。

图1 某区域一天电量随电价变化情况 Fig. 1 The change of daily electricity with electricity price in a certain area

对数据进行标准化处理，公式为：

式中：Xi为数组X的第i个量；Yi为Xi标准化之后的值；为X的平均值；Xstd为X的标准差。

标准化处理，可以减少真实数值的差异，凸显变化趋势。

可以通过2个向量夹角的余弦值，来评估向量的相似度。

设向量为A=(a1,a2)，B=(b1,b2)，则这2个 向量的余弦相似度可表示为：

式中：θ为向量的夹角。

若以时间为横坐标，数值为纵坐标，则可将 相邻两时刻的电价和电量表示为向量(1,Pi-Pi-1)和(1,Qi-Qi-1)。将这2个向量代入式（2），即可 计算出电价与电量向量夹角的余弦值。该值可以反映出用电量因电价变化而出现的变化趋势，称之为电价敏感度。

某时刻的电价敏感度计算如下：

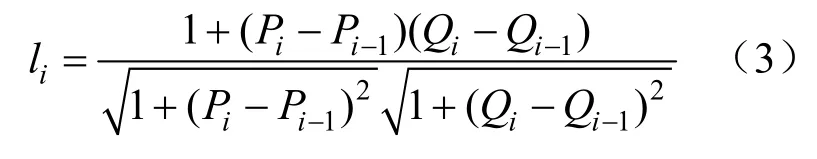
式中：li为i时刻的电价敏感度；Pi为i时刻的电价，Qi为i时刻的用电量。

li取值区间为(-1,1)。li值接近于1，说明电价与电量的变化趋势相似，电价敏感度低；li值接近于-1，表明电价与电量的变化趋势差别较大，电价敏感度高。

本文将强弱判断界限设置为l=0。

通过统计各地区在一个时间段内电价敏感度高的时刻总数，就可比较出各地区电价敏感度的水平。在制定电力市场需求响应政策时，可以据此优先考虑电价敏感度高的地区。

2 响应电量评估

2.1 电价弹性系数

在电力市场中，电能作为一种商品，可以采用需求价格弹性来计算响应电量[15]。

由于地区的用电情况复杂，故本文只使用自弹性系数来评估地区的响应电量。

自弹性系数iiε衡量的是，同时段内电价变化 对电量的影响情况[16,17]，定义如下：

式中：Qi、Pi分别为i时刻的电量和电价；QΔi、ΔPi分别为i时刻相较于上一时刻的电量和电价变 化量。

利用需求价格弹性系数可以计算需求响应电量，公式为：

定义响应电量误差计算公式：

式中：δ为误差；QT为响应电量真实值；QF为由式（5）计算得到的响应电量值。

2.2 分级价格弹性系数

定义波动率为：

式中：v为波动率；umax、umin分别为样本u的最大值和最小值。

图2、图3示出了图1算例中区域AE、PN、DPL这3个地区2021年7、8月份62 d同时刻的用电量和电价情况。

图2 7—8月同时刻用电量变化图 Fig. 2 Diagram of electricity consumption change at the same time in July and August

图3 7—8月同时刻电价变化图 Fig. 3 Diagram of electricity price changes at the same time in July and August

从地区电价和电量变化趋势来看，同一地区2个月内的用电量波动达到92.2%；电价波动更大。

根据经济学原理，在不同的用电量和电价水平下，弹性系数会大相径庭；据此计算出的响应电量也会相去甚远。

针对根据总体弹性系数计算响应电量不准确的问题，本文提出分级弹性系数概念。

采用k-means聚类算法对地区的用电量和电价进行聚类。

k-means算法：根据特征，将一组样本划分为k个无交集的簇。在一个簇中的样本就认为是同一类。簇就是聚类的结果表现。样本分到一个簇的标准是该样本到这个簇的质心的欧几里得距离大于到其他簇质心的距离。欧几里得距离的计算式为：

式中：x为一个样本点；μ为簇的质心；n为样本点总的特征数；i为组成样本点的第i个特征。

使用轮廓系数来评估聚类的效果，即根据簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来判断聚类的簇数。轮廓系数的计算式为：

式中：a为样本与其自身所在的簇中的其他样本的相似度，等于样本与同一簇中所有其他点之间的平均距离；b为样本与其他簇中的样本的相似度，等于样本与下一个最近的簇中的所有点之间的平均距离。

轮廓系数s的取值范围为(-1,1)。当s的值接近1时，意味着相较于其他簇中的样本，该样本与其所在的簇中的样本更相似；当样本点与簇外的样本更相似的时候，轮廓系数就为负。可以总结为，轮廓系数越接近于1越好，负数则表示聚类效果非常差。

在对样本进行聚类之前，用式（1）对样本特征进行标准化处理，以消除样本特征值之间的差异带来的误差。

2.3 异常值剔除

本文使用每天用电高峰时段的电价、用电量来计算价格弹性系数。

考虑电力用户的用电行为会受到电价、天气、节假日等因素的影响，所计算出的价格弹性系数也会出现相应的变化，因此采用3σ原则剔除一些变化过大的值。若

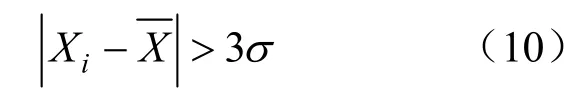
则认为该值为异常值。式中：Xi为第i个样本；为样本均值；σ为标准差。

实际应用中，σ通常不可知。可用样本标准偏差s(Xi)来代替σ：

3 算例分析

3.1 数据说明

结合图1算例，本文使用市场2020年10月1日至2021年9月30日的数据进行分析。数据包括21个地区小时级边际节点电价和对应时刻的用电量信息。

3.2 地区电价敏感度强弱分析

前提条件设定：相邻时刻电价上升变化超过10%，电价敏感度小于0时，认为该时刻电价敏感度高。

各地区2021年7—8月的电价敏感度高的时刻总数如图4所示。

从图4中可以看出，OVEC地区的电价敏感度最高，其次是PN和DPL。

OVEC地区7月份某2 d的电价和电量变化如图5、图6所示。

图5 OVEC地区7月某日的电量电价变化情况1 Fig. 5 The change of electricity price in OVEC area on a certain day in July

图6 OVEC地区7月某日的电量电价变化情况2 Fig. 6 The change of electricity price in OVEC area on a certain day in July

从图5中可以看出，在实时电价的作用下，在用电高峰时段12:00—18:00内，在OVEC的电价出现了大幅上升时，该地区的用电量随着电价的上升出现了明显的下降。

由图6可以看出，受电价影响，该地区出现了用电峰时段比谷时段的用电量少的情况。这表明，该地区对电价变化非常敏感，同时也说明了电价敏感度评价标准的科学性。

3.3 分级价格弹性系数

计算电价敏感度高的地区O VEC、PN和DPL一年用电高峰时段参与需求响应时的自弹性系数。采样3σ原则剔除异常值，然后使用k-means聚类算法对这3个地区进行聚类，筛选出轮廓系数大于平均轮廓系数的样本计算各簇的弹性系数。

图7为PN在3个质心时的聚类图。

图7 PN地区聚类图 Fig. 7 PN area cluster diagram

经聚类分析，筛选出轮廓系数大于平均轮廓系数的样本，得到各簇对应的特征范围如表1所示。

表1 聚类特征范围 Tab. 1 Table of cluster feature range 电价/(美元·MW-1·h-1)

计算出各簇和总体的弹性系数，即分级弹性系数，结果如表2所示。

表2 分级价格弹性系数 Tab. 2 Graded price elasticity coefficient

从表2可以看出，由于用电量和电价的水平不同，弹性系数相去甚远。

针对PN地区，选取该地区7、8月峰时段出现需求响应时刻的数据，分别利用分级弹性系数和总弹性系数计算响应电量；利用式（6）计算误差。计算结果如表3所示。表3中，真实值为用电量的实际削减值的平均值。

表3 PN地区响应电量 Tab. 3 Response power in PN area

由表3结果可见，采用分级弹性系数计算的响应电量具有更小的误差。

4 结论

本文实现了从电价敏感度和响应电量2个维度的地区需求响应潜力评估。根据地区用电量和电价，定义了电价敏感度的计算方式，以此来评估地区参与需求响应的积极性；采用k-means聚类算法定义了分级价格弹性系数，据此可以更加精确地评估地区响应电量。最后用真实数据验证了本方法的科学性。

基于这2个评估维度，在调动地区需求响应时，可优先考虑调动电价敏感度高的地区。

使用分级价格弹性系数可更精确地计算响应电量，这有助于电价或激励策略制定得更加合理。

展望：工业用电占比大是我国电力市场的特点，进行需求响应潜力评估时应加以侧重。