含风光电力系统动态环境经济调度的 混合优化

蒋承刚，熊国江,2，陈锦龙，杨 杰，梁婧仪

（1. 贵州大学 电气工程学院，贵州 贵阳 550025； 2. 工业物联网与网络化控制教育部重点实验室（重庆邮电大学），重庆 400065； 3. 贵州电网有限责任公司 电力调度控制中心，贵州 贵阳 550002）

0 引言

在“双碳”目标背景下，风电、光伏等新能源技术得到了快速发展，装机容量不断提高[1]。

风电、光伏出力具有不确性，有必要在电力系统调度模型中对其充分考虑，进而提高风光消纳力度、降低发电成本、减少污染排放。

在电力系统调度模型中，通常利用概率模型和场景法等应对风电、光伏能源的不确定性[2]。然而，选择一个合适的场景、设置一个适当的概率参数是比较困难的，所以这些方法在实际应用中存在一定的局限性。

电力系统动态环境经济调度（dynamic economic emission dispatching，DEED）是一个典型的高维度、强约束、非线性且非凸的多目标优化问题。在考虑风电、光伏出力不确定性后，模型的求解变得更加复杂。

当前，DEED的非线性优化问题求解主要以智能优化算法为主。

文献[2]针对基本径向移动算法易陷入局部最优解问题，提出一种结合种群变异和引入惯性权值非线性递减策略的改进径向移动算法；将该方法用于含风电场的动态经济调度问题求解，结果表明，算法的搜索精度和全局寻优能力有所提高。

文献[3]通过引入排序学习策略对纵横交叉算法进行改进，实现了冷热电联供微电网经济调度问题求解，得到了较低的经济成本解。

文献[4]针对传统粒子群优化算法易早熟收敛等不足，在分析粒子位置和速度状态转移公式基础上，提出了一种基于随机衰减因子粒子群算法，并进行了最优潮流计算；结果表明，原算法的早熟收敛问题得到改善、计算速度得到提高。

文献[5]对传统差分进化算法（differential evolution algorithm，DE）在面对高维性和大规模约束性优化问题时，探索与开采能力弱等缺陷，提出了一种自适应差分进化算法；将算法用于求解动态环境经济调度问题，结果显示算法的收敛性和求解精度得到提高。

在诸多智能优化算法中，DE算法因其控制参数少、结构简单、易实现、求解性能较好等特点，在求解各种优化问题时得到了广泛的应用。文献[6-8]通过与自适应、多策略等算法相结合的方法来改进DE算法，在各类高维度、多约束、非线性优化问题的求解方面取得了较好的成果。

虽然DE算法在电力系统调度问题求解方面展现出了良好的优化性能，但是随着电力系统调度模型的日趋复杂、需考虑因素的增多，DE优化算法呈现出陷入局部最优、求解精度不高等缺陷，已经不能满足求解要求。

考虑旋转备用、网损等因素，通过采用正负旋转备用容量约束来应对风光出力的不确定性，采用归一化系数将发电成本和污染排放双目标函数转化为单目标函数，本文建立了风光并网的DEED调度模型。考虑到DE算法和JAYA算法[9]具有很好的互补特性[10]，提出一种结合DE和JAYA算法的混合优化算法（hybrid differential evolution and JAYA algorithm，HDJ）。

1 目标函数

1.1 发电成本

火电机组发电过程中消耗的燃料成本即发电成本。需考虑机组阀点效应，系统的发电成本目标函数[11,12]可表示为：

式中：C为火电机组总的燃料成本；T为总调度时段；ai、bi、ci为第i台火电机组的燃料成本系数；ei、fi为第i台火电机组的阀点效应系数；为 第i台火电机组的有功出力下限；Pi,t为第i台火电机组第t时刻产生的有功出力；N为系统内火电机组台数。

1.2 污染排放

总的污染排放目标函数[13,14]可表示为：

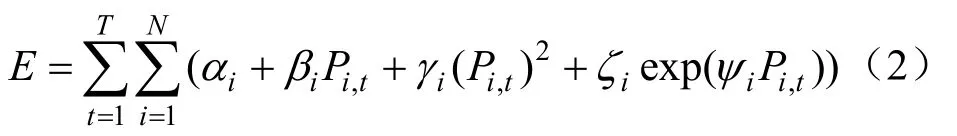
式中：iα、iβ、iγ、iζ、iψ是第i台火电机组的 污染排放系数。

1.3 约束条件

1.3.1 系统功率平衡约束

该约束条件为等式约束，具体表达式如下：

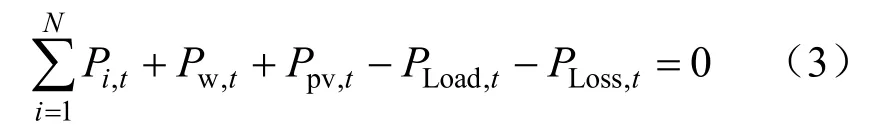
式中：Pw,t、Ppv,t分别是风电场、光伏电站第t时刻的出力；PLoad,t、PLoss,t分别是系统第t时刻的负荷及网损。网损PLoss,t可通过B系数[15,16]法求取，其计算方法如下：

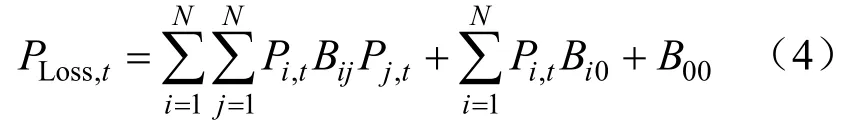
式中：Bij、Bi0、B00是网损系数。

1.3.2 机组有功出力约束

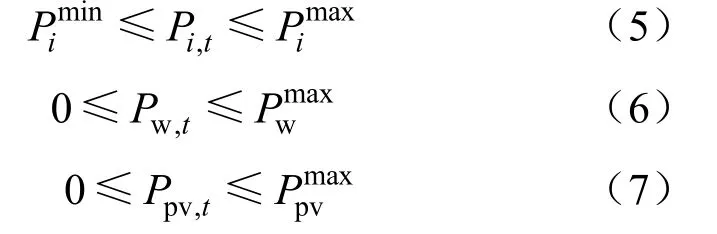
1.3.3 机组出力爬坡率约束

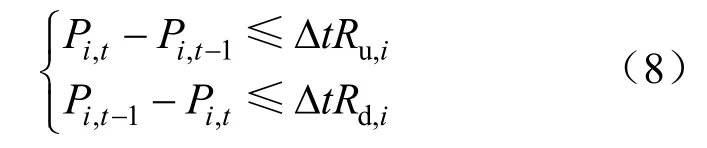
式中：Δt是调度时间间隔；Ru,i、Rd,i分别是第i台火电机组的上升爬坡率、下降爬坡率。

1.3.4 旋转备用约束

（1）正旋转备用

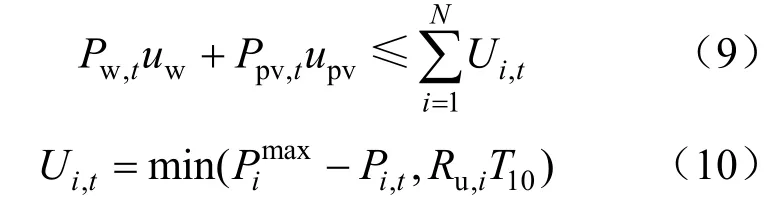
式中：uw、upv分别是风电场、光伏电站第t时刻对正旋转备用的需求系数；Ui,t是系统第t时刻由第i台火电机组提供的正旋转备用容量；T10是选择备用响应时间。

（2）负旋转备用

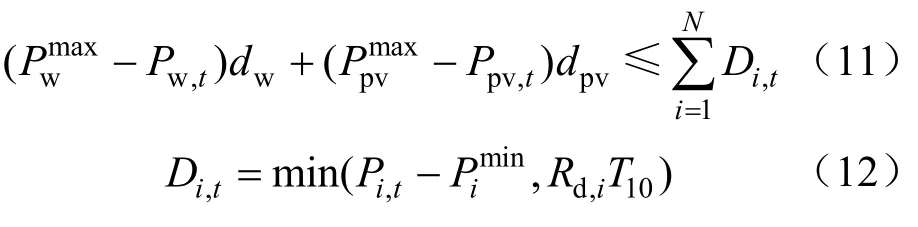
式中：dw、dpv分别是风电场、光伏电站第t时刻对负旋转备用的需求系数；Di,t是系统第t时刻由第i台火电机组提供的负旋转备用容量。

1.4 求解模型

考虑发电成本目标函数与污染排放目标函数相互冲突，本文采用加权求和法[17]，通过将多目标优化问题转换为单目标优化问题来进行求解。

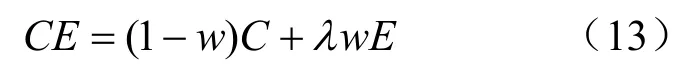
式中：w是权重因子；系数λ由式（14）决定，其表示最大发电成本与最大排放量之比。

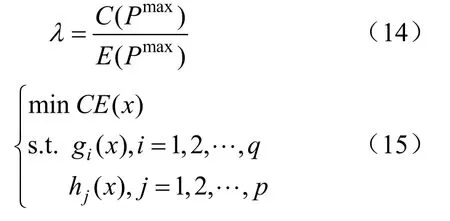
式中：q，p分别为等式约束个数和不等式约束个数。

1.5 最优折中解选取

采用模糊数学方法[18]计算帕累托最优解满意度，以帮助调度员选择最优折中解。单个帕累托解在某个目标函数上的满意度为：

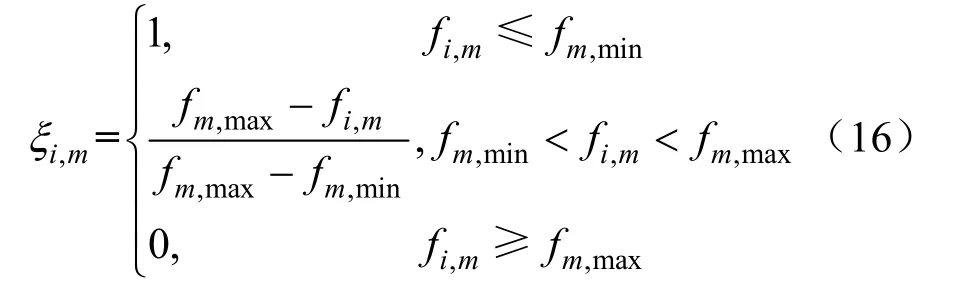
式中：fm,max、fm,min是第i个解的第m个目标函数的最大、最小值。

帕累托最优解满意度：

式中：Nc为POF（pareto optimal front）上解个数。

选择满意度最大的帕累托最优解作为最优折中解。

2 基于HDJ算法的DEED模型求解

将DE和JAYA算法进行结合，本文设计一种混合优化求解方法HDJ。具体操作步骤如图1所示。

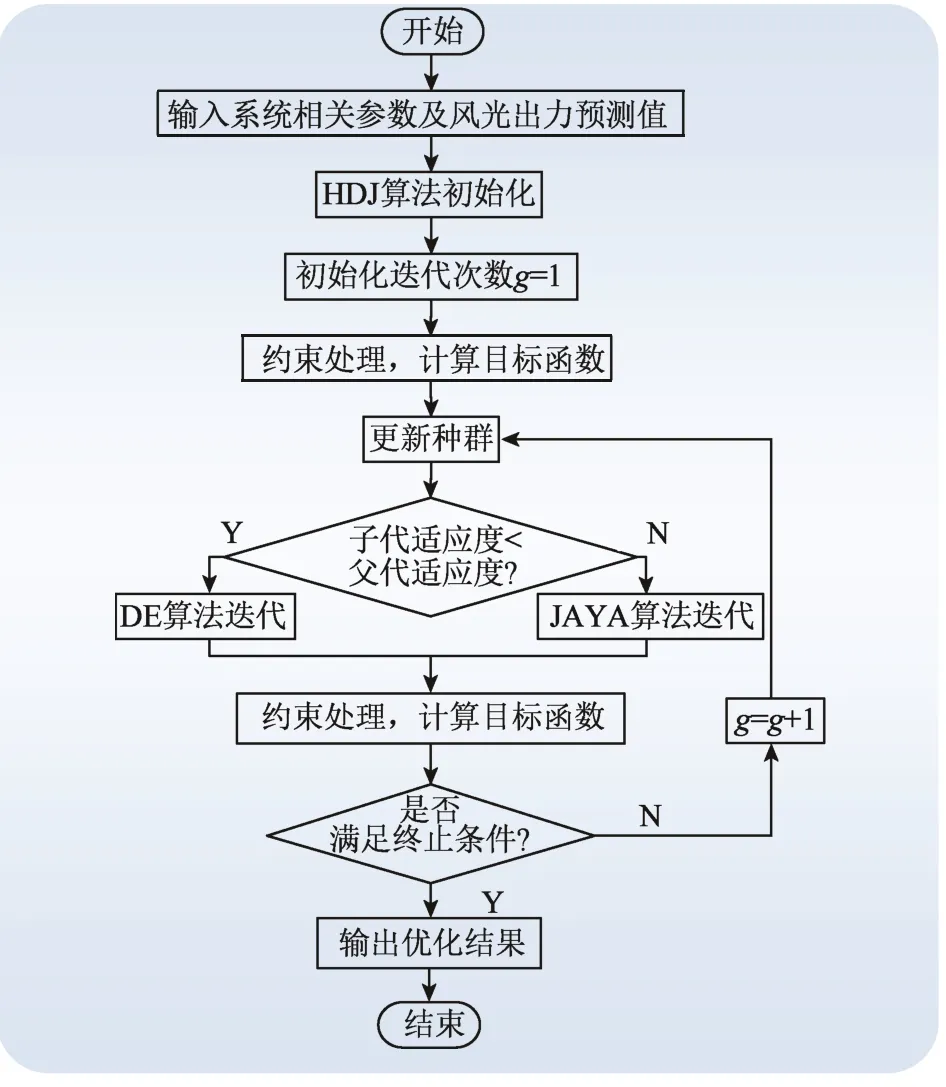
图1 基于HDJ算法的DEED求解流程 Fig. 1 Solution process of HDJ for DEED problem

在该方法中，首先使用DE算法对种群个体进行优化，求解得到一个试验个体。如果新求解的DE算法解决方案比之前的试验个体好，则DE算法继续对种群个体进行优化求解；否则，将由JAYA算法取代DE算法进行种群个体优化求解。

在求解目标函数值前，需要对系统约束进行处理，以满足约束条件。本文采用文献[19]所提出的免惩罚函数约束处理方法处理约束条件。

3 仿真算例及结果分析

以10机组系统[20]为仿真算例，验证所建调度模型的可行性以及所提出HDJ算法的有效性。

10机组系统以1个24 h调度周期为基准，每个调度时段设置为1 h。

为分析HDJ算法的优化性能，将其与DE、JAYA以及CHDJ （competitive hybrid differential evolution and JAYA algorithm，CHDJ） 算法[10]进行对比。种群大小取100，最大目标函数迭代次数取1 000。各算法均独立进行30次运算。

系统并入了1个风电场和1个光伏电站，其额定功率均为100 MW。两者24 h的出力预测值见表1。

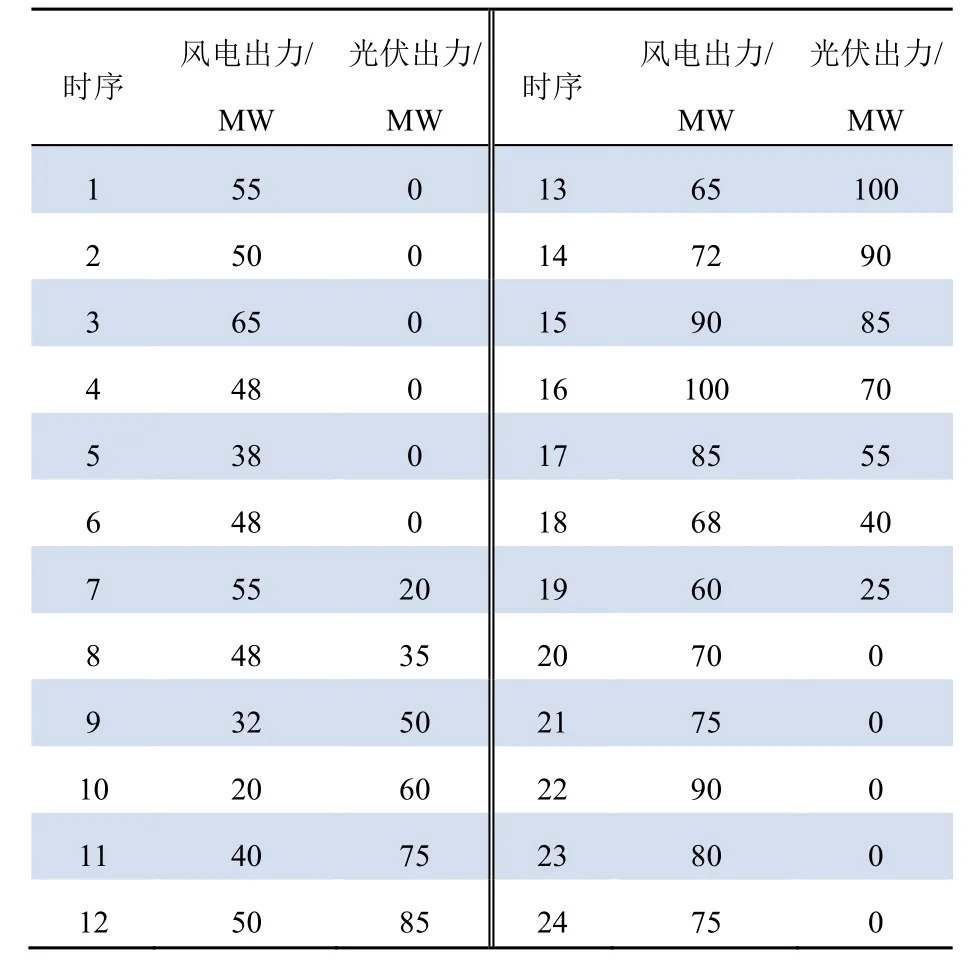
表1 并网风电场及光伏电站时序出力预测值 Tab. 1 Predicted time-series output of grid-connected wind farm and photovoltaic power plant

为克服风光出力不确定性给系统带来的影响，采用正负旋转备用进行应对：正旋转备用需求系数取0.2，负旋转备用需求系数取0.3。

3.1 无风光并网电力系统模型

为验证本文所提HDJ算法的可行性及有效性，首先在不考虑风电和光伏的10机组系统上进行仿真试验，结果见表2。

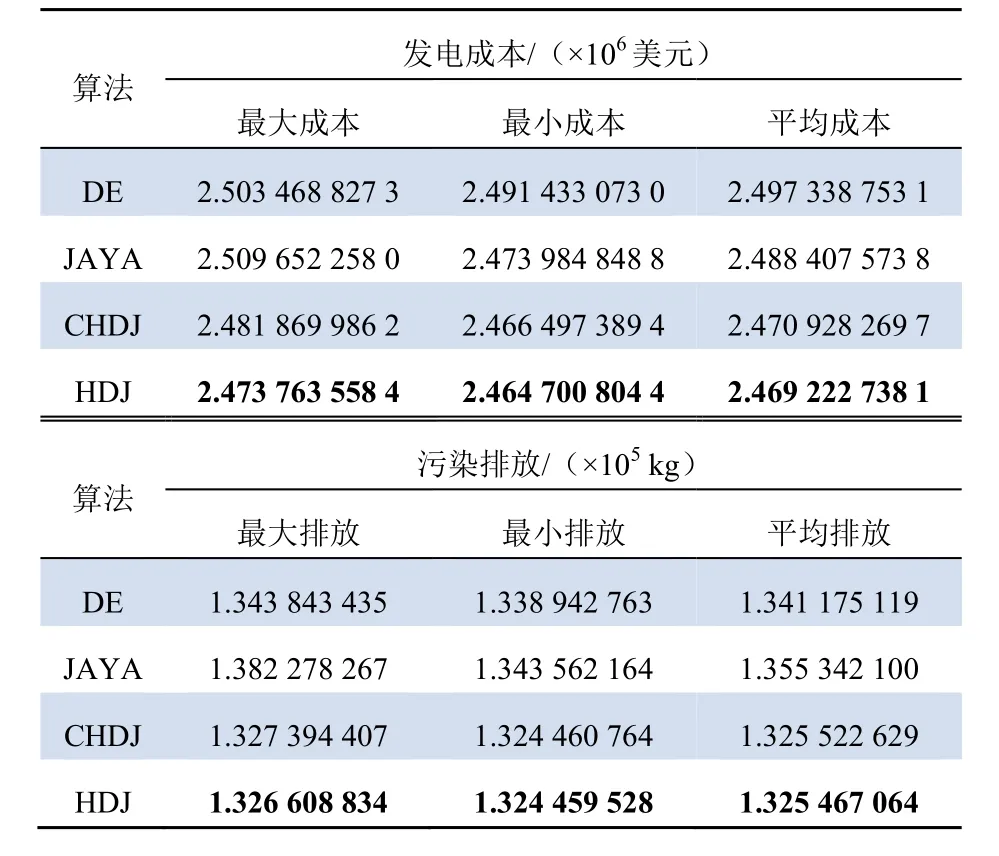
表2 10机组系统仿真结果（30次运算） Tab. 2 Simulation results of 10 units system (30 operations)

由表2数据可知，与DE、JAYA、CHDJ算法相比，本文提出的HDJ算法求解得到的发电成本和污染排放最小。

将极值解及最优折中解列于表3中。由表3可看出，HDJ算法的解最优。

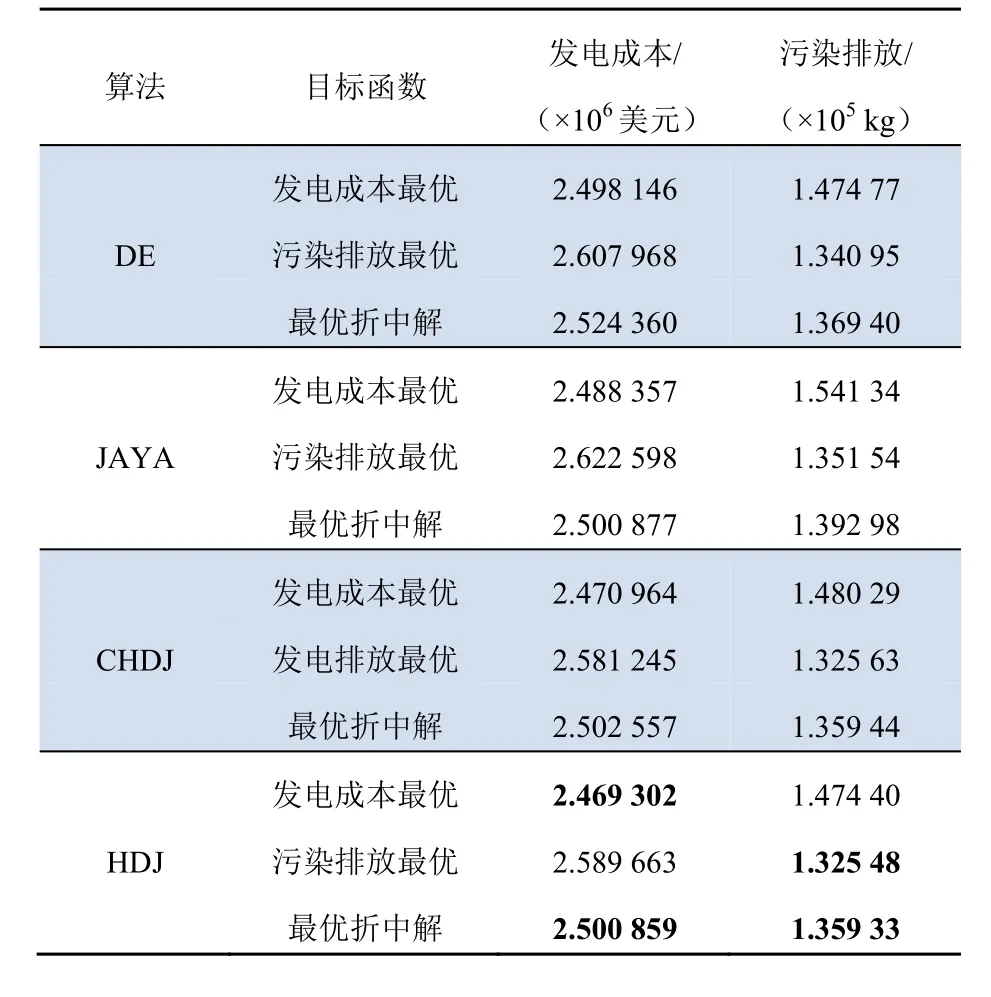
表3 DE/JAYA及其结合体求解得到的极值解和 最优折中解 Tab. 3 Extreme solutions and best compromise solutions obtained by DE/JAYA and its combination

HDJ算法与DE、JAYA及CHDJ算法求解得到的Pareto最优前沿（POF）对比情况如图2所示。由图2可以看出，HDJ的POF更靠近坐标交叉点，这说明其优化性能更好。

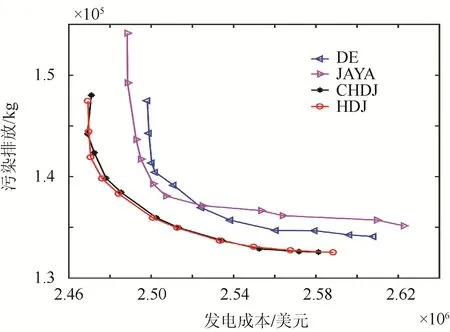
图2 DE/JAYA及其结合体得到的Pareto最优前沿 Fig. 2 POF obtained by DE/JAYA and its combination

将HDJ算法与其他求解算法进行同机组系统求解结果横向比较，比较结果见表4。

表4 不同算法求解得到的极值解和最优折中解 Tab. 4 Extreme solutions and best compromise solutions obtained by the different methods

由表4可知，HDJ算法求解的最优发电成本和最优污染排放分别为2.469 302×106美元和1.325 48× 105kg，结果均最优。与MOVCS算法相比，虽然HDJ算法在污染排放上多了300 kg，但是在发电成本上却比MOVCS算法少了8 241美元。综合考虑，与其他求解算法相比，HDJ算法具有更好的全局搜索能力和求解精度，可获得更优的经济和环境效益。

为证明HDJ算法求解结果的可信度，检验了发电成本最优、污染排放最优及最优折中解。最优折中解的结果如图3所示。各项数据均满足系统约束条件。

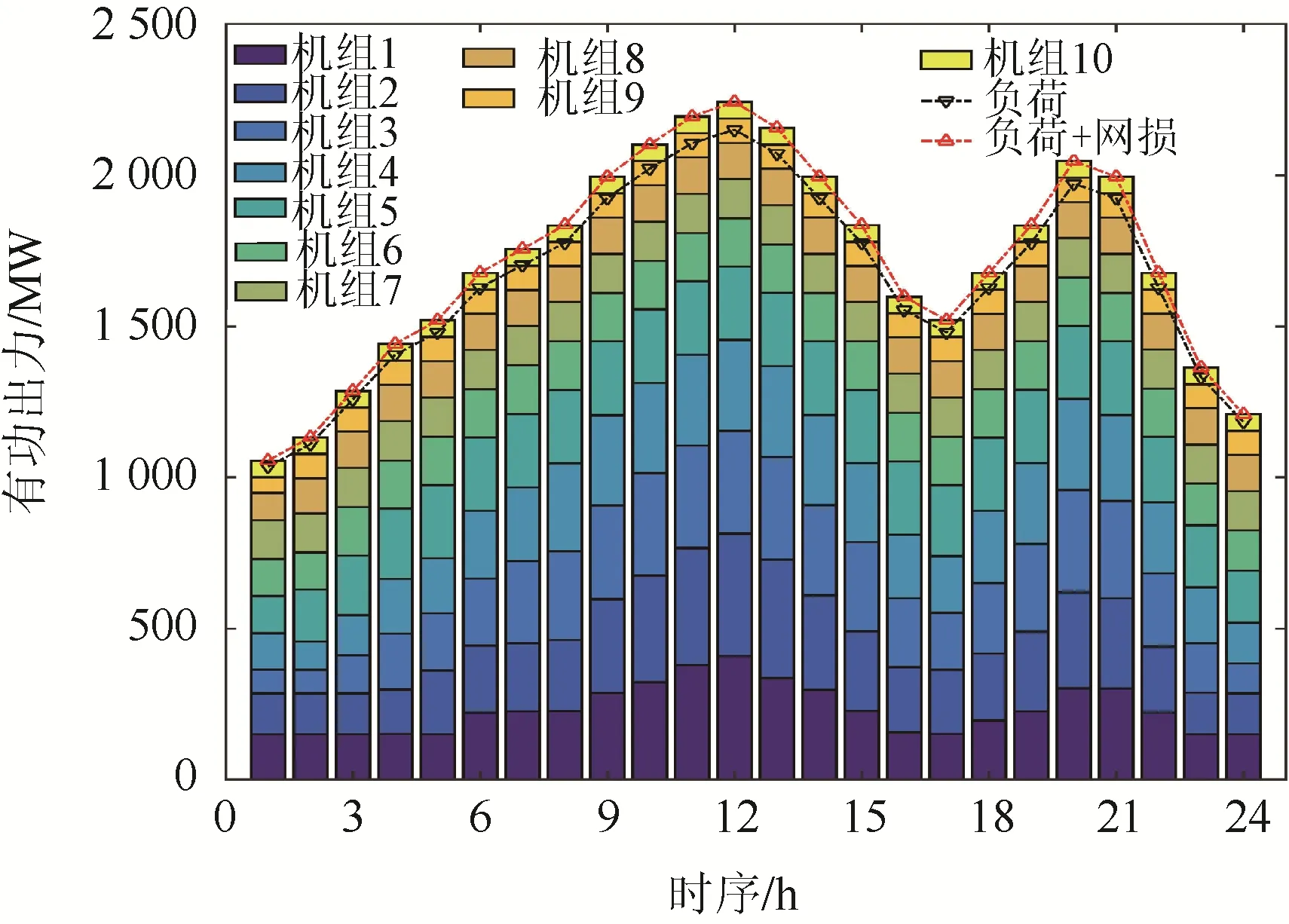
图3 HDJ算法的最优折中解 Fig. 3 Best compromise solution obtained by HDJ

3.2 风光并网电力系统模型

风光并网后，DE、JAYA、CHDJ与HDJ算法各自30次运算仿真结果如表5所示。

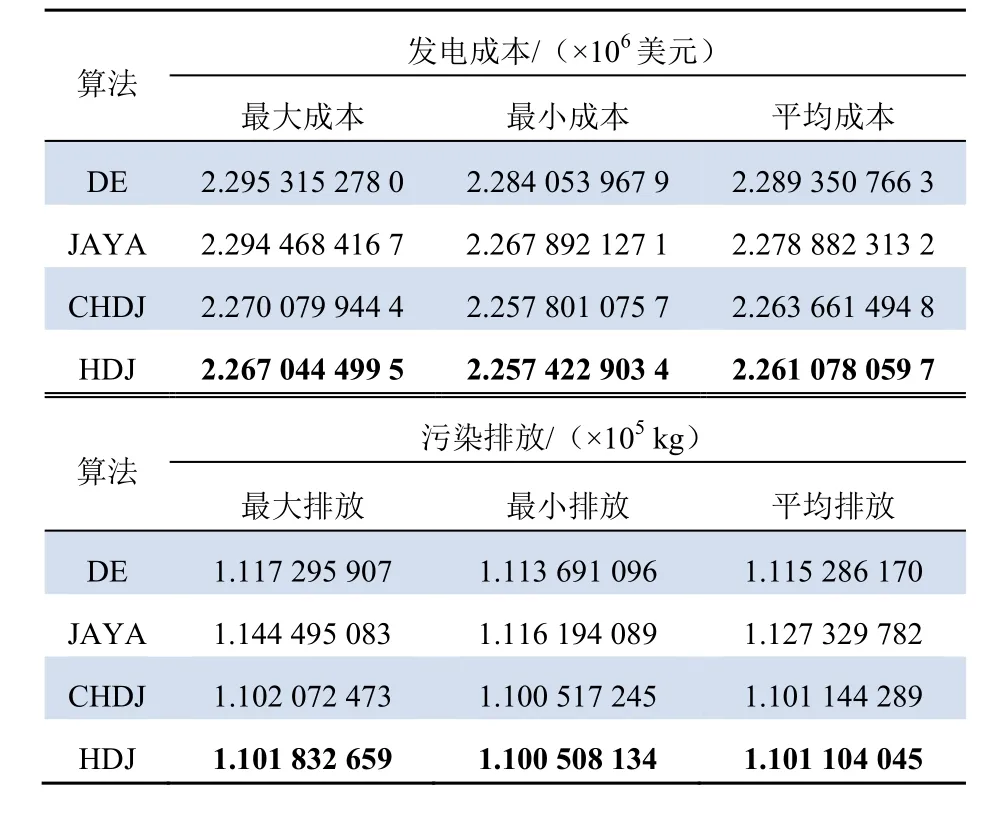
表5 风光并网系统仿真结果（30次运算） Tab. 5 Simulation results of wind-grid connected power system (30 calculations)

由表5可知，在不确定性负荷风光出力并网后，用本文提出的HDJ算法求解调度模型得到的发电成本和污染排放结果依然是最小。

风光出力并网后，各算法的极值解和最优折中解列于表6中，各算法求解得到的POF对比结果如图4所示。

表6 DE/JAYA及其结合体求解得到的极值解和 最优折中解 Tab. 6 Extreme solutions and best compromise solutions obtained by DE/JAYA and its combination

由表6和图4可看出，HDJ算法的POF与CHDJ算法的POF之间的距离差变得更大。这说明HDJ算法的优化性能在考虑风光不确定性后相比其他算法更优。

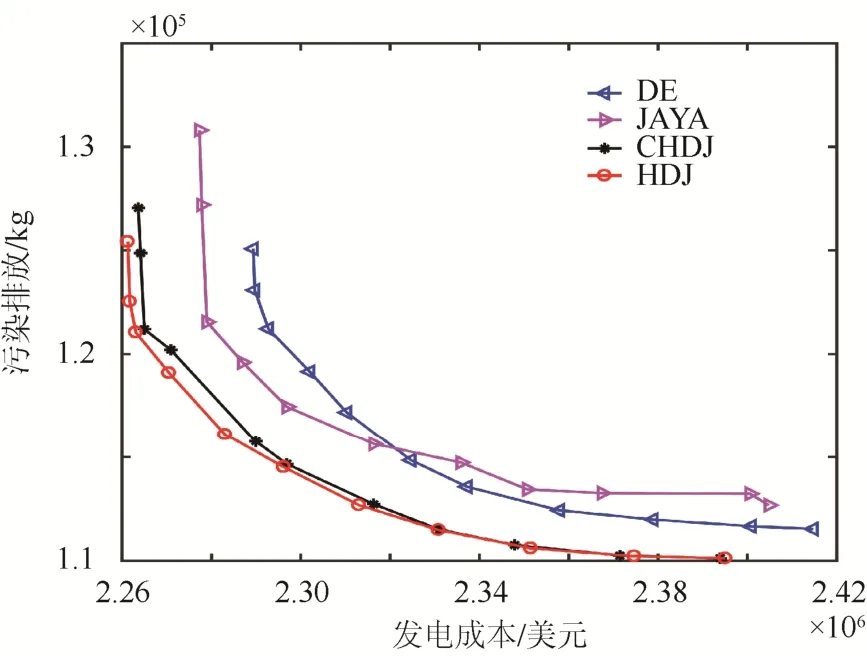
图4 DE/JAYA及其结合体得到的风光并网 Pareto最优前沿 Fig. 4 POF for wind grid connection obtained by DE/JAYA and its combination

HDJ算法求解得到的极值解和最优折中解结果均满足系统各个约束条件，其中最优折中解如图5所示。

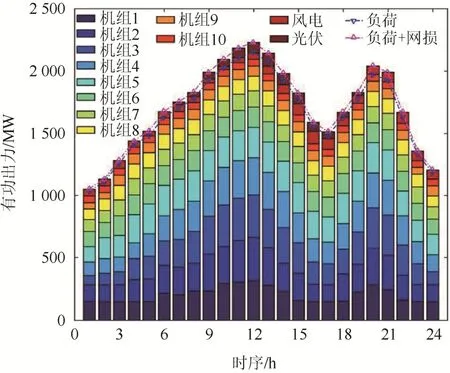
图5 风电并网后HDJ算法的最优折中解 Fig. 5 Optimal compromise solution of HDJ algorithm after wind power grid connection

HDJ算法求解得到的最优发电成本为2.261 289×106美元，最优污染排放为1.101 15× 105kg；与风光并网前求解得到的最优发电成本及最优污染排放相比，计算结果分别减少8.42%和16.92%。同时，风光并网后求解产生的总网损为1 139.18 MW，比风光并网前求解得到的总网损1 298.50 MW减少12.27%。可见，在风光并网后，不仅发电成本、污染排放减少，网络损耗也得到降低。

4 结论

针对风电、光伏出力不确定性带来的影响，建立了风光并网电力系统的DEED模型。通过引入归一化系数，将发电成本和污染排放双目标问题转化为单目标问题，并利用模糊数学方法求解出兼顾经济和环境的最优调度方案。

将DE算法和JAYA算法相结合，设计了一种HDJ混合优化算法，用于求解所建立的DEED模型，提升了算法的全局搜索能力和求解精度。

风光并网后，采用本文算法求解出的方案，系统发电成本和污染排放分别减少8.42%和16.92%，网损减少12.27%，产生了直接的经济和环境效益。