基于动态博弈的武器装备体系发展规划论证方法

陈启宏，赵青松，*，邱 薇，陈 甲

（1.国防科技大学系统工程学院，湖南 长沙 410073；2.中国人民解放军96901部队，北京 100094；3.广东省军区综合训练队，广东 广州 510501）

0 引 言

武器装备体系是在一定的战略指导、作战指挥和保障条件下，为完成一定作战使命，而由功能上相互联系、相互作用的各种武器装备系统组成的更高层次的系统。武器装备体系发展规划，是决策者基于作战背景、目标需求、资源约束等条件，增强武器装备系统之间的协同作战能力，寻找武器装备发展的最优方案，实现武器装备体系整体作战效益最大化的决策过程。因此，武器装备体系发展规划将直接影响武器装备体系结构以及体系之间的影响关系，是适应未来一体化联合作战趋势、提升体系总体作战能力需要解决的重要问题。

目前武器装备发展规划研究已经取得了许多显著性成果。文献［6］从不确定信息的角度出发，同时考虑不同决策者的目的、决策偏好，提出了基于目标规划的武器装备发展方案选择模型，采用层次分析（analytic hierarchy process，A HP）法对主要分析成分设置权重比例，对模型进行求解。文献［7］提出了一种武器装备发展方案的评价模型：通过三角模糊函数将定性指标和语义信息等进行规范化处理，利用AHP对武器装备发展方案的层次结构进行了分析并确定了相应的权重，利用逼近理想解排序法（technique for order preference by similarity to an ideal solution，TOPSIS）原理对武器装备发展方案进行排序。文献［8］基于能力满足度，利用非线性优化算法对网络信息武器装备体系进行优化，得到比较满意的优化路线。

大部分武器装备体系发展规划研究只考虑了装备之间的协同关系，只研究自身武器装备体系发展规划而忽略了对战双方武器装备体系发展规划过程中的博弈对抗特征以及对战双方装备之间的威胁关系。

目前，基于博弈的武器装备体系发展规划的研究主要集中于武器装备体系的构建和演化研究，包括对武器装备体系的对抗博弈进行作战网络结构建模分析和仿真优化。文献［16］和文献［17］对武器装备体系的动态博弈过程进行建模和仿真分析，将演化仿真与博弈论结合，提出了武器装备体系结构演化博弈方法及分析框架。文献［18］考虑了对战双方不断研制新装备与反制装备的对抗过程，构建了军事资源最优化分配模型。此外，还有一些针对具体场景的研究应用，解决武器装备采购、军事运输、军事竞争等实际问题。

但是，上述研究也存在以下不足：①装备之间的协同配合考虑不足；②大部分研究集中于发展武器装备种类的宏观层面，只关注发展哪些武器装备，很少关注什么时候发展、发展周期、采购数量和时间等具体实施层面；③往往只考虑己方的武器装备发展，却忽略实际装备发展博弈对抗中对方装备的发展情况。

因此，本文考虑武器装备发展规划的体系对抗特点，基于博弈论的方法来建立武器装备体系发展规划动态博弈框架，构建了博弈方各阶段策略集合已给出，策略选择信息不完全（概率表示）的不完全信息武器装备发展规划动态博弈模型，研究分析博弈方不同策略下演化形成的博弈脉络，评估博弈方策略在不同博弈场景下的威胁能力以及博弈方全局博弈过程总体威胁能力。

1 武器装备体系对抗网络模型

武器装备体系是由具备侦察、信息处理、决策、火力打击等功能的装备单元连接形成的复杂系统。基于OODA（observe-orient-decide-act）作战理论提出的作战环是将武器装备体系作战过程视为一个循环过程，形成作战环，具体可分为标准作战环和广义作战环，如图1所示。标准作战环中装备实体数量为4个，每个功能类只包含一个装备实体。广义作战环中，装备实体数量超过4个，相同功能类的装备实体之间存在指挥控制、协同替换、信息传递等关系，装备实体的关联作用关系愈加复杂。

图1 标准作战环与广义作战环示意图Fig.1 Schematic diagram of standard operation loop and generalized operation loop

基于OODA作战理论分析，本文将武器装备功能分为3类：侦察功能、指控功能、打击功能。将武器装备实体抽象为4类功能节点：侦察节点、指控节点、打击节点、目标节点，如表1所示。其中，红蓝双方的功能节点互为对方目标节点。一个武器装备实体在任务过程中可以承担多个功能类型，抽象为武器装备体系网络中多个不同类型的功能节点，构建形成不同的标准节点作战环和广义节点作战环。

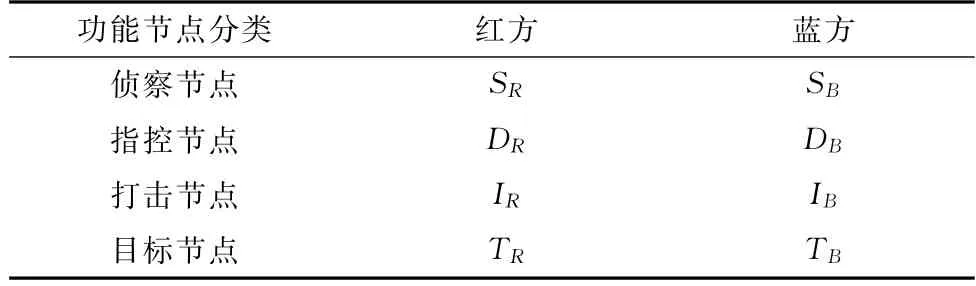
表1 武器装备功能节点分类Table 1 Classification of weapon equipment function nodes

考虑红蓝双方在对抗条件下的边关系建模，武器装备体系中装备之间的关系可抽象为功能边，装备功能节点之间的作用关系可分为4种，如表2所示。在武器装备体系发展规划中，各个功能节点通过功能边关联联系，构建形成不同的作战环，交织形成武器装备体系复杂网络。

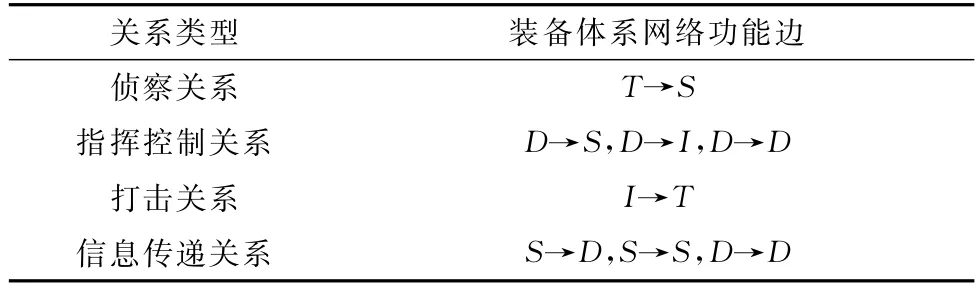
表2 装备作用关系与网络功能边的对应关系Table 2 Correspondence between equipment action relationships and network function edges

根据武器装备体系网络功能边关系，构建武器装备体系对抗网络示意图，如图2所示。

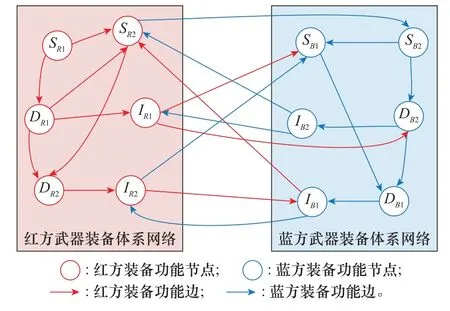
图2 装备体系对抗网络示意图Fig.2 Equipment system confrontation network diagram

2 武器装备体系规划动态博弈过程

武器装备体系规划是一个博弈方遵循异步序贯模式，多阶段推进的动态博弈过程。各博弈方的行动有先后顺序，后行博弈方可以获取先行博弈方策略、决策等有关信息后再进行策略的选择，从而进一步影响下一阶段的博弈过程。且在武器装备体系发展规划过程中，博弈方往往无法获取敌方发展规划的完全信息，因此武器装备体系规划属于不完全信息的动态博弈过程。

简化起见，对武器装备体系发展规划过程做出如下假设：

（1）由于多方博弈比较复杂，设置武器装备体系发展规划的博弈方为红蓝双方。

（2）各阶段博弈方策略集已经给出。不完全信息表现为策略选择的不确定，不确定一方采取特定策略条件下另一方会采取某种具体策略，采用贝叶斯概率来描述另一方选择策略的可能性大小。

（3）武器装备体系发展规划中，只考虑武器装备的研制费用、研制周期和购置费用。武器装备采购列装后，不考虑退役情况，且装备的维护成本忽略不计。

2.1 博弈要素分析

博弈论着重于分析博弈方策略选择之间的相互影响关系，突出博弈方之间合作和对抗的对立统一关系。博弈的基本要素有：局中人、策略集、赢得函数。

（1）局中人：本文中局中人为红蓝双方决策者。＝｛，｝，其中代表红方，代表蓝方。

（2）策略集：各类武器装备发展方案，＝｛（W ，t，N ，），（W ，N ）｝。

其中，武器装备发展方案的决策对象分为待研制装备和已列装装备，决策变量如表3所示。

表3 发展规划方案决策变量Table 3 Development planning scheme decision variables

利用龚帕兹（生长）曲线描述待研制装备研制强度、研制费用和研制周期之间的关系。研制周期和研制费用的表达式为＝（-）·A ＋（ln＞0，＞1），变化趋势如图3所示。

图3 研制强度、研制周期、研制费用之间的关系Fig.3 Relationship among strength，cycle and funds

其中，研制强度＝｛0，1，2，3｝，＝0时，代表不研制该武器装备；＝1时，随着研制费用投入增大，研制周期开始缩短，但费用不足仍是周期研制的主要限制约束，缩短幅度较小；＝2时，投入的研制费用较为充足，随着研制费用投入增大，研制周期的缩短幅度较大；＝3时，人才、技术成熟程度、资源等成为研制周期的主要限制约束，研制周期缩短幅度较小，当下降至最短研制周期后保持不变。

（3）赢得函数：在武器装备体系发展规划的过程中，红蓝双方不断进行博弈对抗，基于掌握的博弈信息，调整各阶段的策略方案，反制降低对方的体系威胁能力。因此，红蓝双方的赢得函数为：在一方进行反制的动态博弈条件下，另一方发展规划方案在不同博弈场景对其造成的体系威胁能力均值。

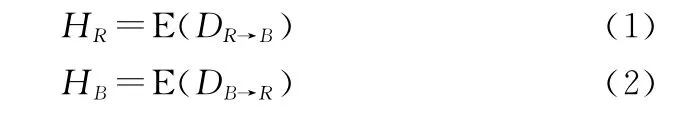
2.2 动态博弈局势构建

在武器装备体系规划的动态博弈中，博弈方并非绝对理性，会根据自身利益的改变不断调整自身方案。假设红方作为博弈先行方，每个阶段中，红方先做出决策时，蓝方根据红方的策略，对己方武器装备发展方案的偏好发生改变，趋向于选择改善自身利益的策略。上一阶段博弈双方的方案决策又会对下一阶段博弈方的方案决策产生影响，从而形成一个博弈方之间“你来我往”的反复博弈过程。

在博弈过程中，博弈方选择不同的武器装备发展规划方案映射在武器装备体系网络中加入不同的武器功能节点。为了抵抗或削弱对方武器装备对己方带来的威胁，博弈双方会选择相应的武器发展方案加入新的装备功能节点对对方的功能节点（目标节点）进行反制打击，使得武器装备体系对抗网络变得越来越复杂化，如图4所示。

图4 动态博弈过程Fig.4 Dynamic game process

以图4的第2阶段为例，简述武器装备发展规划的动态博弈过程：在第1阶段红蓝双方方案选择前提。在第2阶段中，红方首先研制新的武器装备，新增功能节点I对蓝方的功能节点S 和D 进行打击。蓝方作为后行方选择新增功能节点I 对红方的功能节点I 和S进行打击，同时S被蓝方的装备节点回路覆盖，代表节点被反制，对蓝方的威胁能力降低。在第3阶段中，红方将在第2阶段红蓝双方的方案基础上，进一步考虑自身的方案决策。

设定威胁能力系数u 描述一个功能节点被对方装备不同数量节点作战环反制打击的效果，如图5所示。

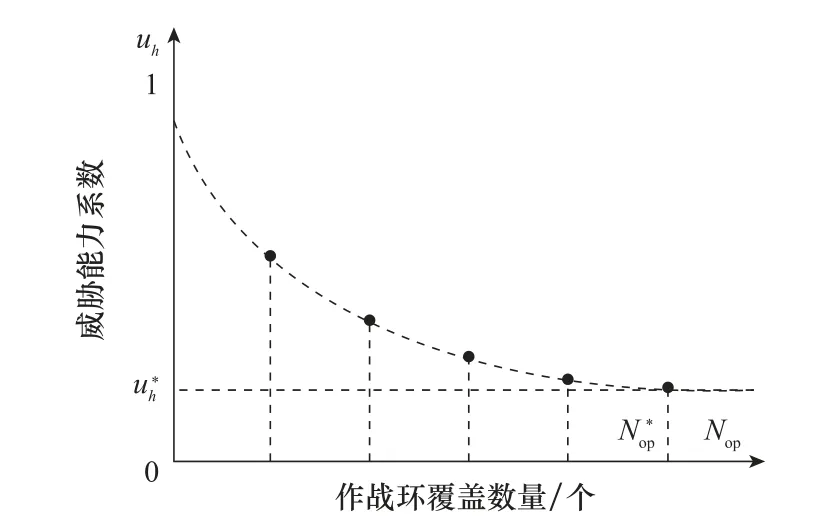
图5 威胁能力系数Fig.5 Threat capacity coefficient

武器装备功能节点威胁能力系数u与对方装备节点作战环的覆盖数量（∈N）的关系为

3 武器装备发展方案威胁能力评估

明确博弈双方各阶段的武器装备发展方案，用采取方案概率的大小描述博弈方根据对方的策略选择，趋于改善自身效益的己方方案偏好程度。各个阶段博弈方轮流决策构成了武器装备体系规划的不同博弈场景。

博弈子场景：每个阶段红蓝双方选取不同博弈策略构成不同的博弈子场景。

博弈全时域场景：将博弈子场景按照时间维联结构成博弈全时域场景，即武器装备体系演化的一种具体路径。

博弈全局场景：通过资源约束，得到所有的可行全时域场景集合，构成博弈全局场景，即动态博弈树，如图6所示。

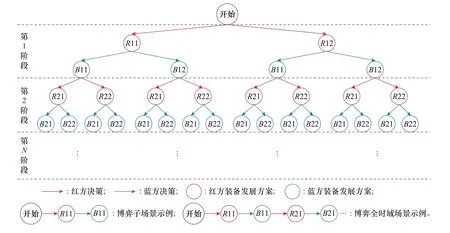
图6 动态博弈树（博弈全局场景）Fig.6 Dynamic game tree（game full situation scene）

通过体系网络功能指标的规范化和资源约束，明确武器装备体系发展动态博弈树的可行演化路径（即可行的武器装备发展方案）。通过计算各个武器装备发展方案对应的红蓝双方武器装备体系网络中包含的标准作战环和广义作战环威胁能力之和，评估武器装备发展方案对敌方体系的威胁能力。

（1）明确资源约束，规划可行域。

资源约束主要包括费用约束和时间约束。费用约束主要考虑两个方面：各个阶段投入的费用不能超过各个阶段的费用约束；各个阶段投入的费用总和不能超过总费用约束。

时间约束主要考虑整个博弈过程的总时间约束。所有装备的采购和研制过程都应该在给定的规划期内进行。

（2）构建博弈子场景，计算各阶段子赢得函数。

在每个阶段，红蓝双方的博弈不同策略可以组成不同的博弈子场景。在博弈子情景下，计算武器装备体系网络下不同样式作战环的威胁能力。

计算标准作战环威胁能力：作战环的威胁能力主要取决于侦察、指控和打击3类节点的功能评价值。由于标准作战环只包含4个节点，标准作战环的侦察、指控、打击能力对应侦察、指控、打击节点的功能评价值。设定侦察节点、指控节点和打击节点的功能评价值为d ，d ，d 。采用乘积形式计算标准作战环的威胁能力，同时考虑对方作战环覆盖数对已方功能节点的影响，设定标准作战环威胁能力的计算公式为

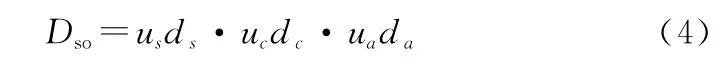
式中：u ，u，u 分别代表标准作战环侦察、指控、打击3类节点的威胁能力系数。

计算广义作战环威胁能力：由于广义作战环中同功能类（侦察、指控、打击）下的节点数量不唯一，对广义作战环的侦察、指控、打击能力产生影响。因此，在计算广义作战环威胁能力前，需要计算广义作战环的侦察能力d 、指控能力d 和打击能力d 。假设一个广义作战环中包含个信息传递关系的侦察节点，侦察节点之间存在信息传递和协同控制关系，则广义作战环的侦察能力d 计算公式为

结合计算得到的侦察、指控、打击能力，采用乘积形式计算广义作战环的威胁能力为

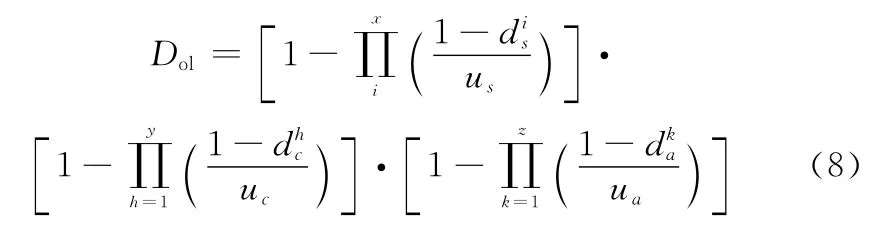
计算各阶段的子赢得函数（以计算红方对蓝方的体系威胁为例）：设第个阶段红蓝双方中红方对蓝方的标准作战环数量为，广义作战环数量为，则红方第个阶段对蓝方的威胁能力值D

→为

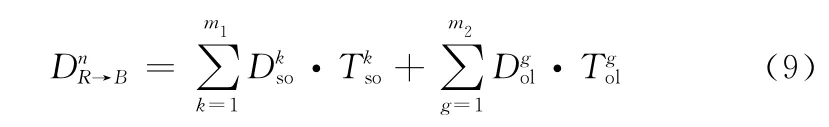
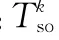
（3）构建全时域场景，计算全时域赢得函数。

将博弈子场景按照时间维联结起来构成全时域情景，得到各全时域情景下的赢得函数为

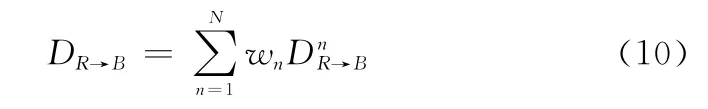
式中：为发展规划的阶段总数；w 为各阶段子赢得函数在全时域赢得函数的风险偏好系数。

入学教育是一项全面系统的工程，要依靠学校统筹教学资源、协调院系以及相关部门共同参与才能推进，现实情况多是研究生入学教育仅由学生工作部门承担，或者是依托培养院系自行设计完成，学校职能部门、学院系所教师、导师团队、在校学生等均普遍缺乏参与意识，使研究生入学教育越来越被边缘化。而且传统的适应性、集体式的入学教育并不能满足研究生的个体发展需求，无法适应人才培养的需要，需要系所、实验室、科研团队等更多与研究生实际学习生活联系更为紧密的队伍参与到入学教育中来。

计算各全时域情景的发生概率。以红方作为先行方，全时域情景G发生的概率为

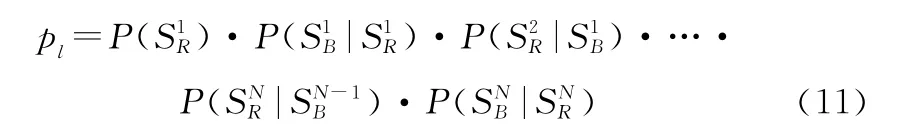
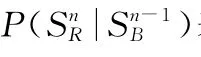
（4）构建全局场景，计算全局赢得函数均值。

通过资源（时间和费用）约束，确定出可行的全时域情景集合，并对发生的概率进行归一化处理，得到可行的全时域情景的概率分布。所有的可行全时域情景集合形成全局情景，依据归一化处理后的概率，分别计算红方和蓝方在全局情景下的赢得函数期望值。通过红蓝双方赢得函数期望值的大小来判断红蓝双方的总体威胁能力强弱。

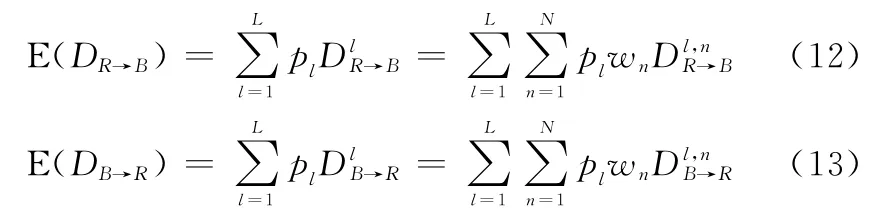
式中：为可行全时域场景总数；p 为第个可行全时域场景的发生概率。

4 示例分析

设定武器装备发展规划阶段分为两阶段，周期为10年，前5年为第1阶段，后5年为第2阶段。红蓝双方的费用约束均为30亿元，红蓝双方的武器装备代号以及武器装备的功能指标仿真值（归一化处理，0值代表不具备该功能）、武器装备的采购价格如表4所示。

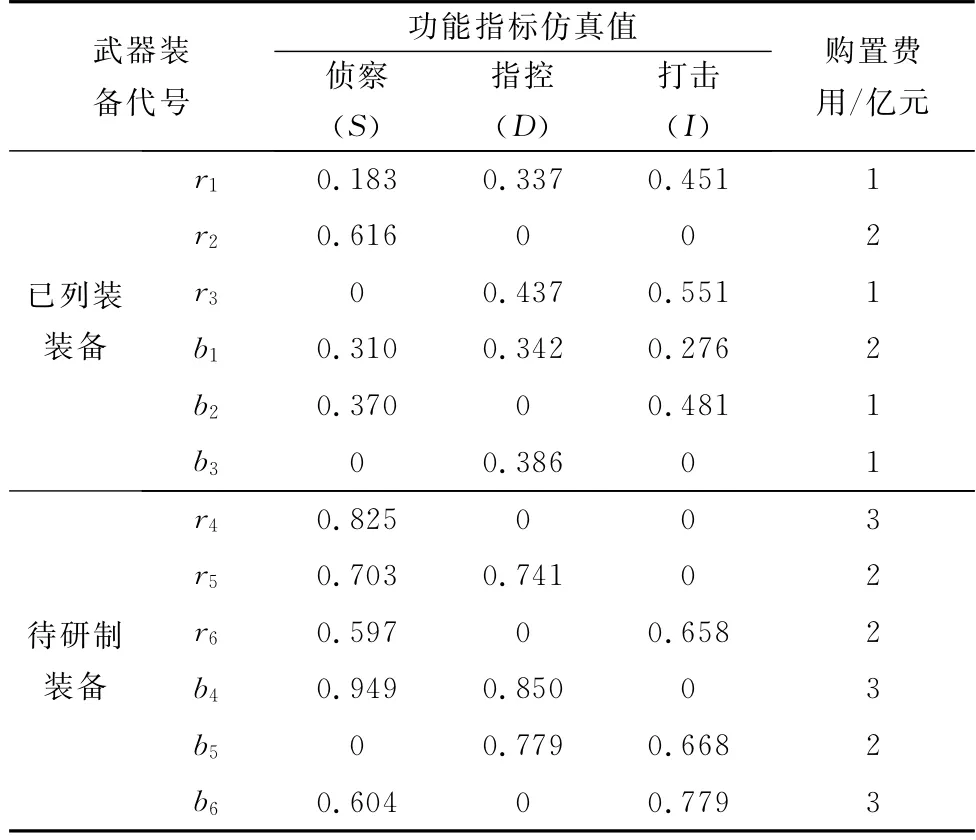
表4 装备功能指标值、购置费用表Table 4 Function indicator and purchase price list of equipment

假设红蓝双方每个阶段的策略集都为两个。第1阶段，红方的策略集为11＝｛第1年采购3件，3件，投入6亿元研制（＝2，＝3）｝，12＝｛第1年采购2件，4件，1件，投入4亿元研制（＝1，＝4）｝；蓝方的策略集为11＝｛第1年采购1件，2件，2件，投入4亿元研制（＝2，＝3）｝，12＝｛第1年采购2件，3件，2件，投入3亿元研制（＝1，＝4）｝。第2阶段，红方的策略集为21＝｛第6年采购1件，投入6亿元研制（＝3，＝1），第8年采购2件｝，22＝｛第6年采购1件，1件，投入6亿元研制（＝2，＝2），第8年采购1件，2件｝；蓝方的策略集为21＝｛第6年分别投入5亿元和4亿元研制（＝2，＝2）和（＝2，＝3），采购1件，第9年采购2件，第10年采购1件｝，22＝｛第6年采购1件，投入5亿元研制（＝2，＝3），第8年采购2件｝。其中，红蓝双方待研制武器装备的研制强度和研制周期（单位为年，数值均已经过整数化）由设定的龚帕兹（生长）曲线得到。

各个阶段的策略集按照时间维联结得到红蓝双方多阶段方案。根据装备功能节点连接关系，设定红蓝装备体系的功能边关系如图7所示。功能节点中的数字代表武器装备发展方案。某个功能节点中包含数字，该功能节点对应的武器装备包含在该武器装备发展方案。

图7 红蓝装备体系的功能边关系Fig.7 Function side relationship of red and blue equipment system

以红方作为先行方，双方多阶段策略选择的博弈树及概率分布如图8所示，构建成16个博弈全时域场景。以蓝方作为先行方，双方多阶段策略选择的博弈树及概率分布如图9所示，构建形成16个博弈全时域场景。

图8 双方动态博弈树及概率分布（红方作为先行方）Fig.8 Dynamic game trees and probability distribution of both parties（red side as the forerunner）

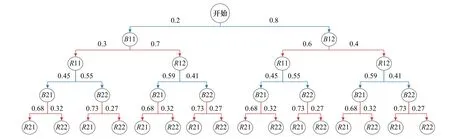
图9 双方动态博弈树及概率分布（蓝方作为先行方）Fig.9 Dynamic game trees and probability distribution of both parties（blue side as the forerunner）

设定武器装备3类功能节点的威胁削弱难度指数a均为1。以红方作为先行方，根据式（4）～式（9），可得不同博弈可行全时域场景下的红蓝策略集各阶段的威胁评估值，如图10所示。

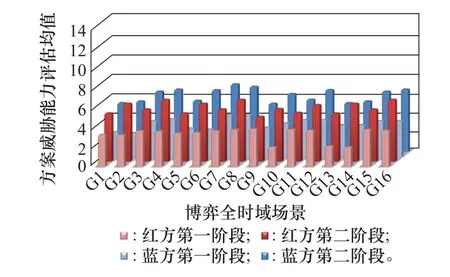
图10 红蓝策略集各阶段的威胁评估值Fig.10 Threat assessment value in each stage of the red and blue policy set

设定决策者对第1阶段的风险偏好系数为0.2，对第2阶段的风险偏好系数为0.8。通过资源约束判断可行全时域场景集合，结合图8和式（11）计算可行全时域场景集合的概率分布，并归一化。根据式（10）计算得到红蓝双方武器装备发展方案在各个可行全时域场景下的威胁评估值，如表5所示。

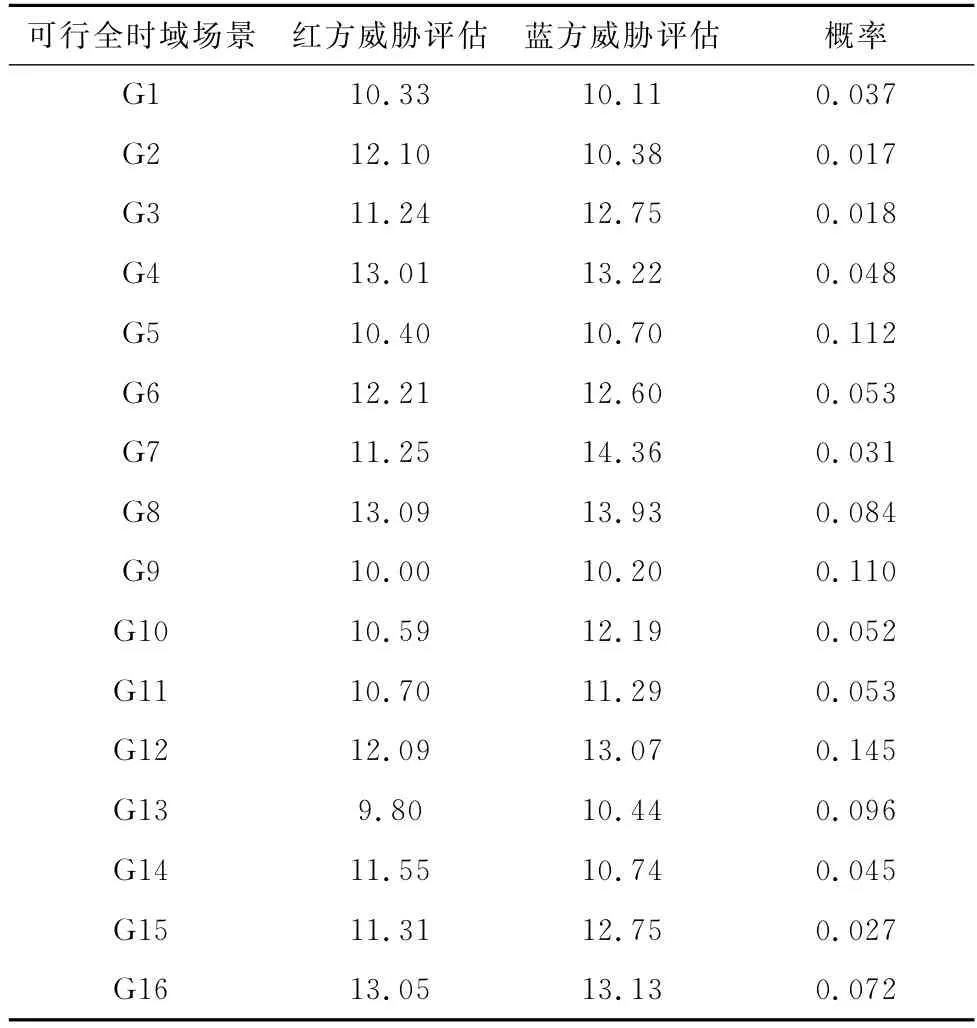
表5 可行全时域场景下的红蓝方案威胁评估Table 5 Threat assessment of red and blue schemes in feasible all-time-domain scenarios

计算红方和蓝方武器装备发展方案在不同全时域场景下的威胁能力均值，以红方方案（11，21）为例，如表6所示。其中概率已经经过归一化处理，同理计算其他方案的威胁能力均值。

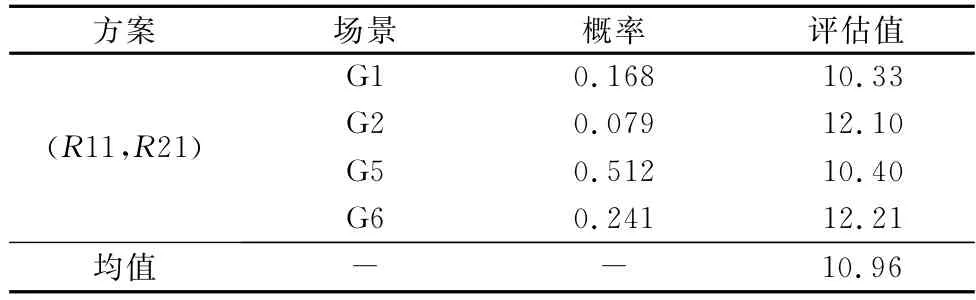
表6 红方方案（R11，R21）威胁能力评估表Table 6 Threat capability assessment of red scheme（R11，R21）

根据式（12）和式（13）分别计算红蓝双方在全局场景下方案威胁能力均值，得到红蓝双方发展方案威胁能力评估结果，如图11和图12所示。

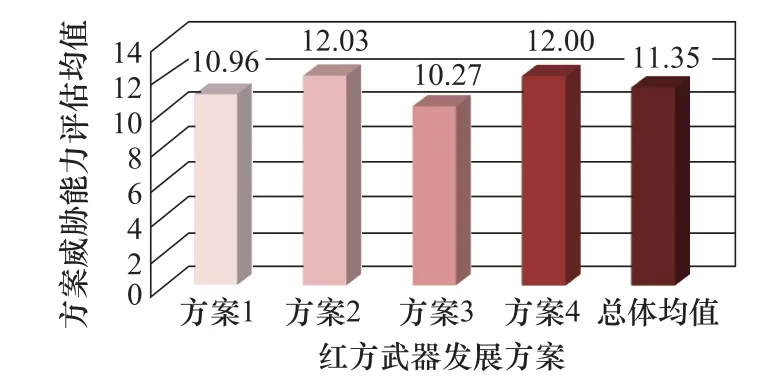
图11 红方发展方案威胁能力评估Fig.11 Threat capability evaluation of the red side’s development scheme

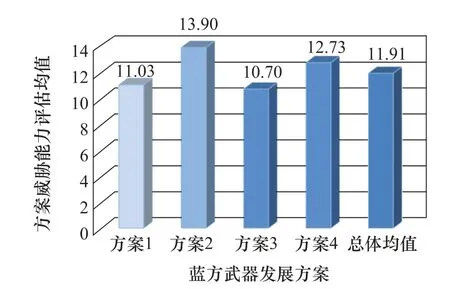
图12 蓝方发展方案威胁能力评估Fig.12 Threat capability evaluation of the blue side’s development scheme

同理，考虑蓝方作为先行方，计算红方和蓝方武器装备发展方案威胁能力的均值，与红方作为先行方的情况进行比较，得到不同先行方的总体均值结果比较，如图13所示。

图13 不同先行方的结果比较Fig.13 Comparison results of different pioneers

现代战争的作战形势日趋复杂，针对不同的作战背景和作战目标，决策者对武器装备体系发展不同阶段的风险偏好系数也会发生变化，影响博弈结果。以红方作为先行方，比较决策者第1阶段不同风险偏好系数对方案威胁评估结果的影响，如图14所示。

图14 第1阶段风险偏好系数对方案威胁能力评估的影响Fig.14 Impact of the first stage risk preference coefficient on threat capability evaluation of the scheme

通过分析发现，在各方武器装备发展方案中，红方方案4（12，22）和蓝方方案2（11，22）的威胁能力在各个全时域情景下的评估均值最大，可作为各方的最佳策略选择。红蓝双方的总体威胁能力大小体现出了双方博弈的强弱比较。而总体威胁能力不仅受单个方案威胁能力的影响，同时还受先行方不同导致的全时域场景概率分布变化以及决策者对各个阶段的风险偏好系数变化的影响。

5 结束语

本文主要开展了基于动态博弈的武器装备体系发展规划论证方法的相关研究，分析双方武器装备体系之间的对抗演化过程。构建基于动态博弈的武器装备体系发展规划的全局博弈脉络，评估红蓝双方不同发展规划方案在不同博弈场景下的威胁能力以及总体威胁能力均值，最后给出了具体示例，并进行了求解和结果分析，为武器装备体系发展规划构建一个新的定量决策模型，也可为类似规划问题提供参考。下一步研究的主要工作包括：进一步优化武器装备发展规划方案的威胁评估方法、如何科学合理地计算确定对方不同策略选择下已方策略选择概率的变化。