基于核Fisher判别的群结构更新模型及群目标跟踪算法

刘浩楠，宋骊平

（西安电子科技大学电子工程学院，陕西 西安 710071）

0 引 言

随着目标跟踪领域的持续发展，针对不同场景下目标跟踪问题的研究也越来越深入。杂波环境下数目未知且时变的多目标跟踪问题是近年来的研究热点。因此，基于随机集的方法已成为多目标跟踪的主流方法，例如概率假设密度（probability hypothesis density，PHD）滤波 器［1］等。文献［2］提出的高斯混合概率假设密度（Gaussian mixture PHD，GM-PHD）滤波器，能够实现线性高斯条件下的多目标跟踪。文献［3］提出的序贯蒙特卡罗PHD（sequential Monte Carlo PHD，SMC-PHD）滤波器，可以解决非线性的多目标跟踪问题。在此基础上，文献［4］提出的箱粒子概率假设密度（box particle PHD，BP-PHD）滤波器，在保证滤波性能的同时，解决了因粒子数目过多导致的计算时间过长的问题。当多个目标聚集在一起，其运动具有相似性，对外表现出群组运动特征时，常常称为群目标，例如无人机集群、舰艇编队等。对于这样的群组目标，有时雷达分辨力并不足以分辨其中的每个个体目标，因此需要将其作为一个整体看待，有时即使可以分辨，也没有必要将其分开。例如，对于火力打击来说，在某些情况下将其看作一个整体来跟踪也是合理的。因此，近年来对群目标跟踪的研究也已成为一个热点问题。文献［5］将群目标分为可分辨群目标和不可分辨群目标。群目标跟踪的提出打破了传统跟踪中目标与量测一一对应的假设，具有态势认知能力［6-7］。对于多个群目标，根据其密集程度，只需要通过跟踪群的质心，就可以完成对多个群目标的跟踪，除了跟踪群中心，有时还需要考虑群的轮廓问题。文献［8］提出使用高斯过程方法对群／扩展目标的扩展形态进行建模。在群目标跟踪中，还需要考虑群的划分，以及群演化过程中的分裂与合并等问题，称之为群结构的建模和更新，具有十分重要的意义。

21世纪初期，Gning等［9-10］对蒙特卡罗方法的粒子滤波实现方式进行了进一步的优化和完善，并且提出了群演化网络模型［9］来对群数目估计和群结构更新，推动了群目标跟踪领域的迅速发展，基于群演化网络模型的群目标跟踪算法不断涌现［11-13］，已成为群结构建模的主流方法。群演化网络模型通过计算目标间的马氏距离与预设阈值进行比较来完成分群操作，但群演化网络模型中阈值需要人为设置，效率较低。

近年来，随着机器学习的快速发展，机器学习算法和思想应用到了各个领域。机器学习的第一次出现是在20世纪50年代，通过训练样本归纳出学习结果，且机器学习算法大多都不需要人为干预。本文将机器学习思想应用到群结构建模中，提出了一种基于核Fisher判别分析（kernel Fisher discriminant analysis，KFDA）的群结构更新模型，KFDA是一种常用于模式识别领域的有监督的机器学习算法［14-16］，从带有标签的训练集中进行学习，得到一个分类模型，输入新数据时通过此模型来推测新实例的所属标签。群结构更新问题可以看作一个二分类问题，即能够组成一个群的目标为一类，不能的则为另一类，通过数据训练可得到符合分群特性的群结构模型。与群演化网络模型相比，KFDA不再单一地依靠阈值来更新群结构，而是通过数据训练出来的模型更新群结构，无需人为干预，当然在实际的作战系统中可以考虑保留人工干预通道。对比实验表明，在相同滤波条件下，所提算法比群演化网络模型跟踪效果更好，群数目估计也更准确。

1 理论基础

1.1 Fisher判别分析

1.2 核KFDA判别

Fisher判别分析方法适用于训练数据为线性可分的情况，当处理高维不可分的数据时，Fisher判别方法表现就远远不如处理线性可分数据。因此，Mika等［17］提出将核函数引入Fisher判别分析方法中来解决这个问题，使其性能大大提升。

KFDA方法首先将原始数据通过特征空间进行高维映射，把非线性数据间接地转换为线性数据，在特征空间内提取特征，转换示意图如图2所示。

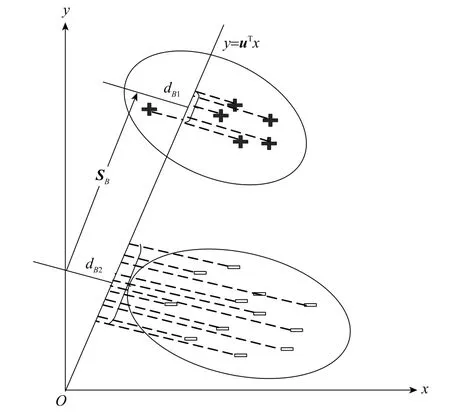
图1 FDA示意图Fig.1 FDA schematic diagram

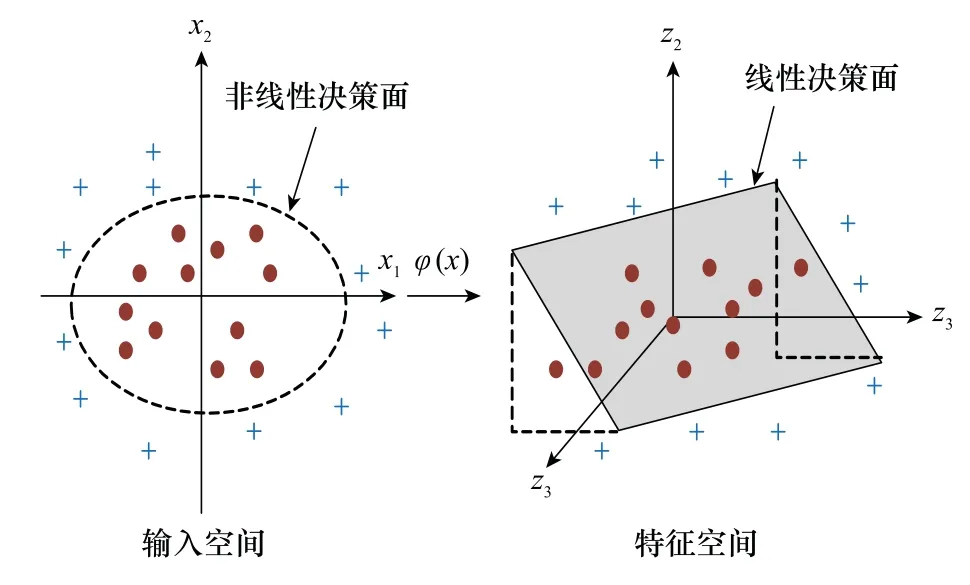
图2 KFDA模型转换过程Fig.2 Transformation process illustration of KFDA model

因核函数不能直接计算，引入函数φ，功能是将数据x映射到希尔伯特空间（特征空间）H，即x→φ（x），φ（x）∈H。令t表示特征空间的维数，那么有φ（x）∈Rt，当x∈Rd时，t≫d。

两个向量x1和x2的核函数就定义为

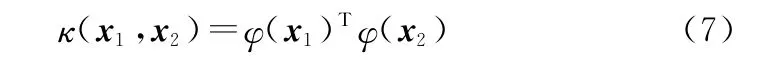
第j类样本在特征空间H中经过映射后的均值记为φ（μj）：

式中：I为单位矩阵；1为全1向量。

在特征空间H中，令θ＝wφ，Fisher判别准则为

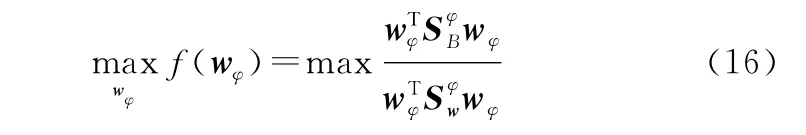
通过数据的不断训练得到符合核Fisher判别准则的wφ。

1.3 群演化网络模型

群演化网络模型用来建模群目标随时间的演化［9］，是一张由顶点与边构成的图，随着时间不断更新，顶点表示目标，边表示目标间的关系。群演化网络模型主要由边的更新、新节点的加入和节点的消亡这几部分组成。

1.3.1 边的更新

假设已知有N个目标，且构成了顶点集合V＝｛v1，v2，…，v N｝，计算任意两个顶点之间的马氏距离，与根据先验知识所预设的阈值进行比较，若所得马氏距离小于预设阈值，则两个顶点间使用边连接，记为E（i，j）＝（v i，v j），认为其同属于一个群［9-10］，通过每一时刻对边进行更新得到当前时刻的群结构信息。因群目标跟踪中涉及目标数目过多，计算边的更新时运算量会很大，所以文献［10］提出以前一时刻的子群中心代替子群内所有目标，形成了一个新的节点集合，从而得到了一个新的群结构，在新的群结构中，只对相邻子群内的节点进行群划分，避免了不相关节点的计算，提高了计算效率。群划分操作示意图如图3所示，边的更新示意图如图4所示。

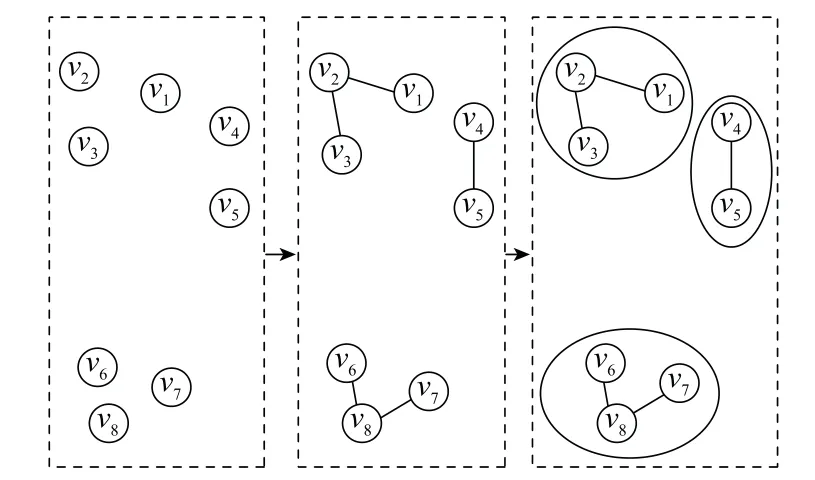
图3 群划分Fig.3 Group division

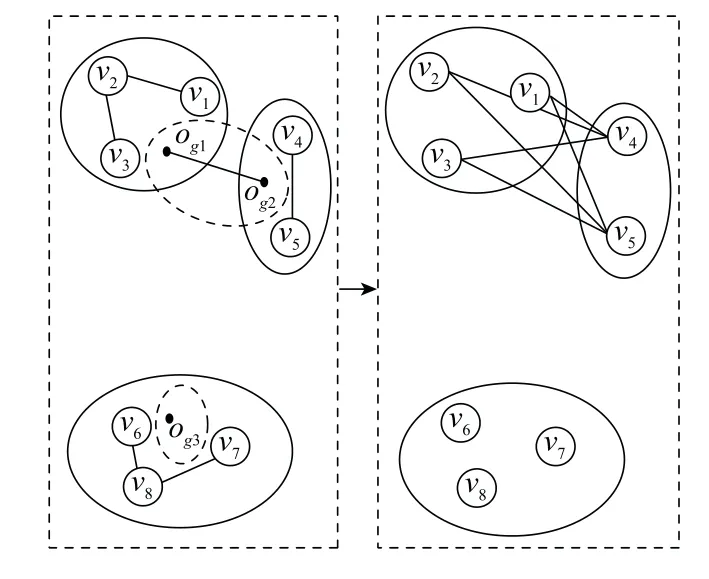
图4 边的更新Fig.4 Update of edge

1.3.2 新节点的加入

当有新节点加入，目标数目变多时，需要多次计算马氏距离，为了减少计算量，参考边的更新时所使用的方法，以子群中心代替子群内所有目标，只需要计算子群中心与新节点间的马氏距离，如果满足条件，则把新节点划分到对应的群中，否则新节点单独成为一个群。新节点加入的示意图如图5所示。

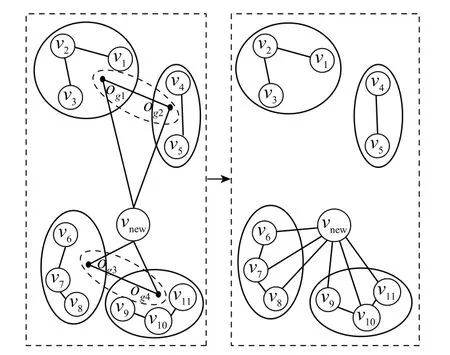
图5 新节点加入Fig.5 Adding new nodes

1.3.3 节点的消亡

当一段时间内，模型中获得的量测信息没有关于某一个节点的信息，那么这个节点就会被认为是一个死亡或者消亡目标所对应的节点，通过移除与其相关的边的信息的方式来删除该节点。

1.4 箱粒子滤波

箱粒子滤波是一种基于区间分析的滤波算法，使用区间变量代替点变量。箱粒子的提出有效解决了粒子滤波所需粒子数过多，计算量过大的问题，也可以借助区间分析解决实际场景中量测的不确定性问题［12］，近年来也常用于群目标跟踪领域。

箱粒子滤波采用大小可控的箱粒子去替代传统粒子滤波中的点粒子，最大限度拟合目标的后验概率密度。

在实际的跟踪环境中，目标和量测都具有不确定性，因此目标的状态集合与量测集合表示为两个随机有限集：

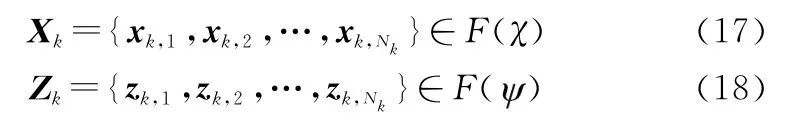
式中：N k为k时刻目标数目；x k，i，z k，i分别代表k时刻第i个目标的状态和量测向量；F（χ），F（）分别代表目标的状态空间和量测空间。

因箱粒子滤波采用区间分析的方法，所以在箱粒子滤波中的量测集合表示为

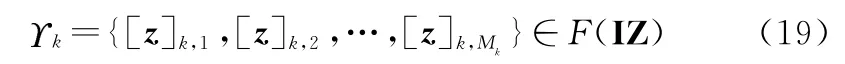
式中：［·］表示区间；F（IZ）表示观测空间；Mk表示k时刻观测到的目标数目。箱粒子滤波的具体算法流程参见文献［18］，限于篇幅，此处不再赘述。

2 基于KFDA的群结构更新模型

传统的群结构更新模型，例如群演化网络模型，如第1.3节所述，需要根据先验知识去设置阈值来对群结构进行更新，对群数目的估计依赖于阈值的选取，阈值的选取对群跟踪精度影响较大。本文提出将KFDA方法应用于群结构更新中，通过训练数据进行训练，得出符合要求的分群模型。在KFDA中把群结构更新问题看作一个二分类问题，一类为目标能够分为一个群，另一类为目标不能分为一个群。训练数据集形式如下：

式中：j为目标标签，或者将目标看作样本时称为样本标签，n j为第j个标签下的样本数量。为了提高模型的泛化能力，使正负样本个数相同。

假设［p1，p2，…，p m］∈G，［q1，q2，…，q s］∉G，m和s为目标个数，p和q代表目标状态向量，｜·｜表示取绝对值，则

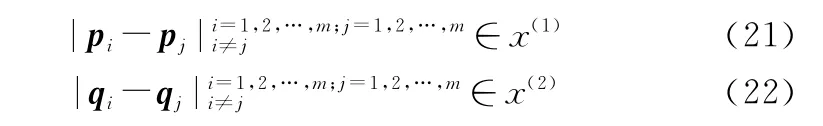
KFDA判别需要通过和来找到使KFDA准则最大的特征向量wφ，在Fisher判别分析中，如果已经给定了训练数据集，那么S B和S W能够被确定，接下来只是让广义Rayleigh Ritz商最大化的过程［19］。但是在KFDA中，根据核函数的特性可知，wφ不能直接计算出结果，所以需要把wφ写成另一种表现形式：

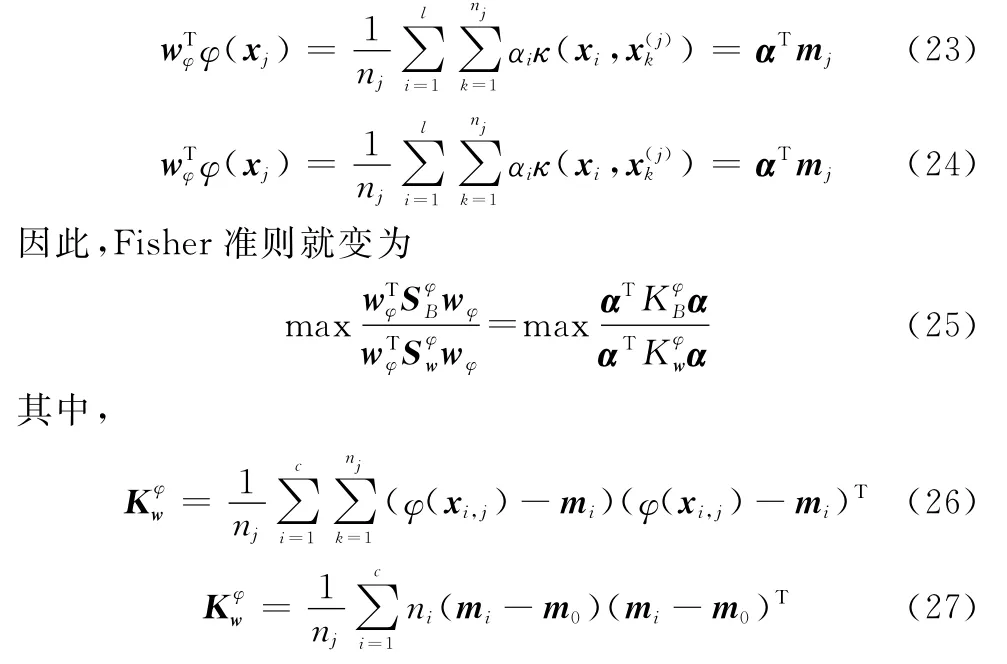
这样求解投影最佳方向向量wφ就转换为求解列向量α的问题，可以等价于求解广义特征方程：

通过给定带有标签的数据集，计算出训练样本和特征参数的关系，得到训练好的群结构模型，在群目标跟踪过程中，当输入的数据预测标签为Group时才划分为一个群，否则不能分为一个群，因此只需要预测标签就可以完成群目标跟踪中对预测量测数据的分群操作。

3 基于KFDA群结构模型的群目标跟踪算法

3.1 目标运动模型

假设群内各个目标的运动模型为CV模型［20］，目标状态方程为

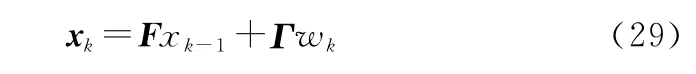
3.2 目标量测模型

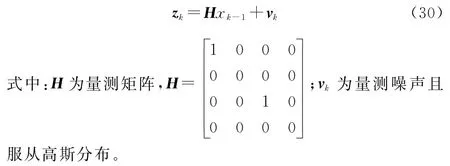
假设目标量测空间Z∈Rz，则k时刻的目标量测方程可以表示如下：

3.3 算法流程

本文采用KFDA群结构更新模型来更新群结构，同时采用箱粒子PHD滤波来跟踪群目标。本文提出的算法整体思想为：通过箱粒子PHD滤波获得目标预测量测，再通过KFDA群结构更新模型来实时更新群结构信息。

3.3.1 箱粒子初始化

初始化过程中，箱粒子集合由存活箱粒子和新生箱粒子两部分组成，即

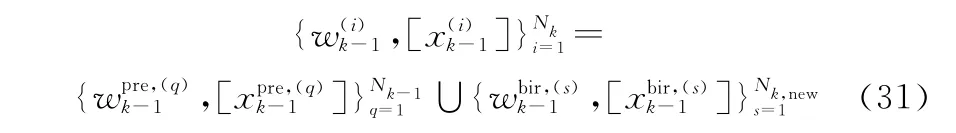
式中：w表示权值；N k-1为k时刻存活粒子数；N k，new为k时刻新生粒子数；k时刻的箱粒子总数为N k＝N k-1＋N k，new。

3.3.2 预测

预测目标状态为

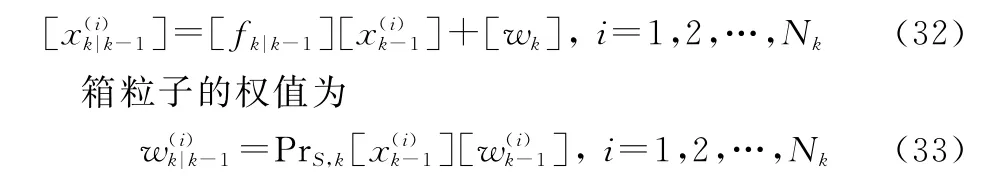
其中：［f k｜k-1］为包含函数；PrS，k为k时刻目标存活的概率。

3.3.3 更新

k时刻箱粒子权值更新为

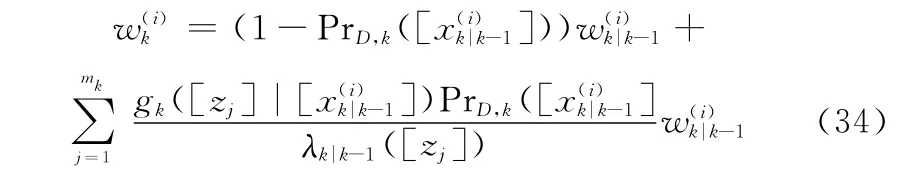
式中：PrD，k为检测到目标的概率；λ为杂波数。

3.3.4 重采样

箱粒子滤波与粒子滤波相似，随着滤波次数的增加会存在着粒子退化问题，为了解决退化问题和保持箱粒子的多样性，要对其进行重采样操作，重采样时采用随机子划分的重采样方法，为保证其多样性，在预测步中，根据上一时刻的量测状态信息实时补充新的箱粒子。

3.3.5 群结构信息更新和反馈

对重采样后的箱粒子集提取目标状态，将提取到的结果送入到训练好的KFDA群结构模型中，通过预测标签来完成分群操作，继而得到k时刻更新后的群结构信息G k，通过Gk来对箱粒子集中属于同一个子群的目标状态进行修正，并使子群内的速度统一，完成群结构信息反馈，得到包含新的群结构信息的箱粒子集。

3.3.6 获取目标状态

由于箱粒子采用了区间分析的方法，因此为了得到目标的状态信息对箱粒子集进行点化操作，使用箱粒子区间状态的中心代替整个箱粒子，最终获得目标的状态估计信息：

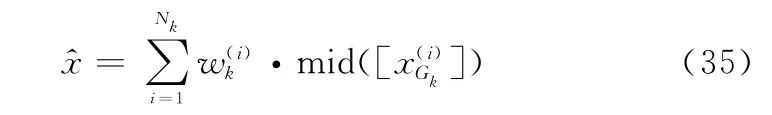
式中：mid（·）表示取箱粒子的中心点。根据群数目估计结合当前目标的状态估计结果进行k-means聚类，得到当前时刻的群中心。

4 仿真实验与结果分析

为了验证本文所提出的群结构模型在群结构更新时的有效性，设计了在箱粒子PHD滤波环境下基于KFDA的群结构模型与群演化网络模型的对比试验，使用群数目估计和最优子模式分配（optimal sub-pattern assignment，OSPA）距离以及群结构的不确定性估计来作为两种模型的评判标准，仿真实验设备为Intel（R）Core（TM）i7-10700，CPU3.80 GHz，Matlab2011。

仿真场景为一个大小［±600 m×±600 m］且伴有随机分布噪声的区域。区域内有8个目标，总运动时长为40 s，目标运动中伴有群的分离和合并，采样间隔T＝1 s，箱粒子数目N＝25，过程噪声w k和量测噪声v k的标准差分别为δw＝［0.05，0.05］；δv＝［2.5，2.5］，箱粒子的区间长度为［14，24］，存活概率PrS，k＝0.99，杂波数量r＝2，OSPA距离参数p＝2，c＝70，目标运动方程和量测方程如式（31）和式（32）所示。

8个目标的位置和速度信息如表1所示，～表示在当前时刻目标运动方向发生改变时所对应的位置信息。

表1 目标真实运动状态Table 1 True states of the targets

目标真实运动轨迹如图6所示，在二维平面上，两种算法的单次蒙特卡罗仿真的跟踪结果如图7所示。在图6中，目标的真实运动轨迹用黑色实线表示，“·”表示真实群中心，蓝色的“⊙”表示目标运动起始位置，“→”表示目标运动方向，并给出了8个目标所对应的标签。

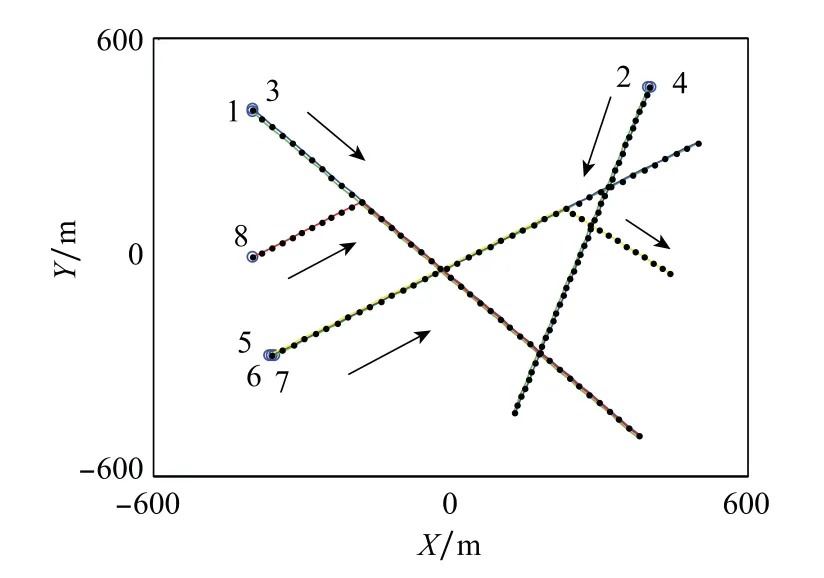
图6 目标真实运动轨迹Fig.6 True trajectories of targets

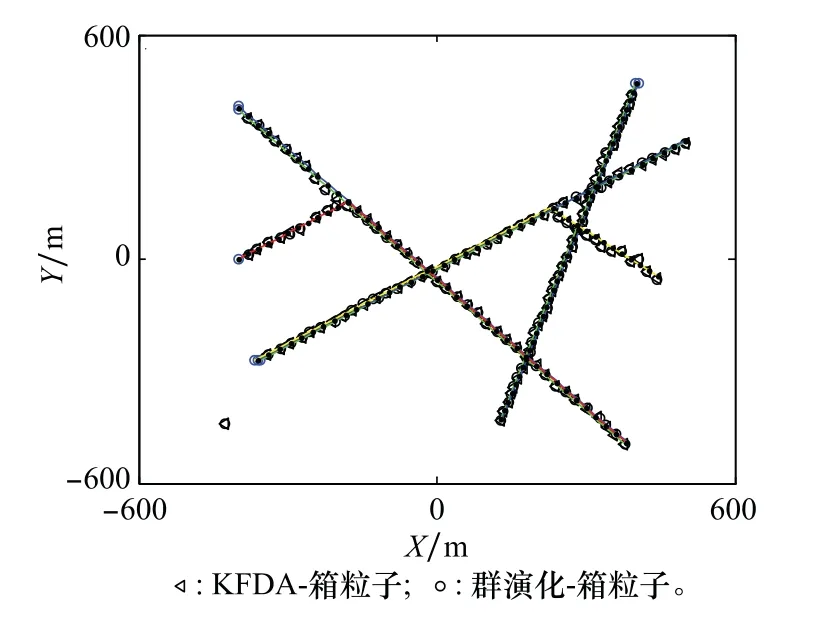
图7 跟踪结果Fig.7 Tracking results

为了更好地验证两种模型的性能，进行了50次蒙特卡罗仿真取其平均值来观察运行结果，群数目估计结果和OSPA距离如图8和图9所示。

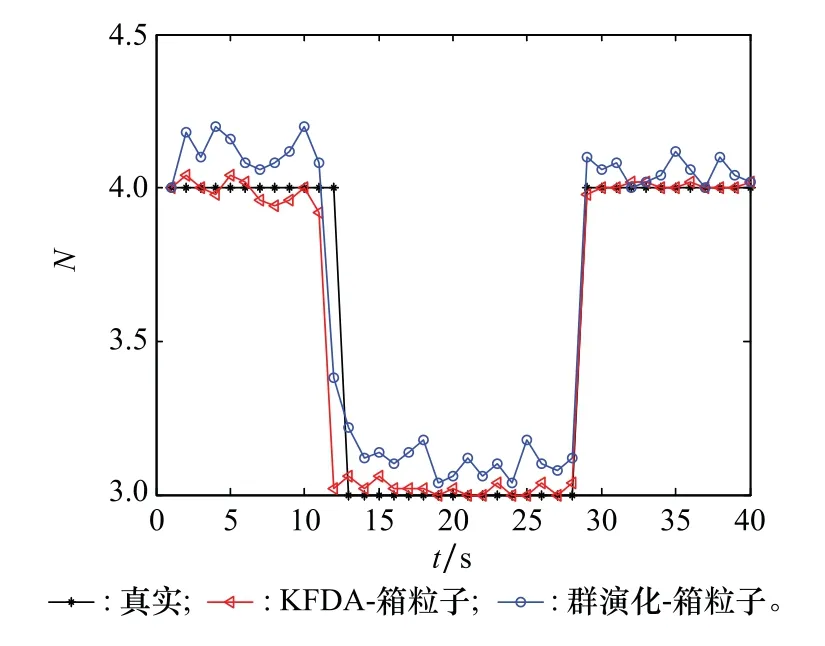
图8 群数目估计结果Fig.8 Group number estimation

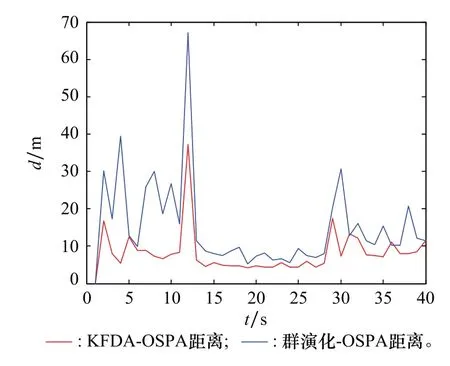
图9 OSPA距离Fig.9 OSPA distance

由图8可以看出两种模型在群数目估计方面都较为准确，但是两者对比来看，通过数据训练出的群结构模型比群演化网络模型在群数目估计方面更稳定，波动幅度更小，全局适应能力更强，且不需要人为干预，模型训练好后，可直接使用。而群演化网络模型中群数目估计效果依赖于阈值的设置，而且设置阈值需要不断尝试，最终才会找到一个比较合适的值，效率比较低。由图9可见，基于KFDA群结构模型的箱粒子PHD滤波器在整个跟踪过程中的OSPA误差要小于基于群演化网络模型的箱粒子PHD滤波器，可见KFDA群结构模型对群数目估计更准确，跟踪误差更小。

图11和图12分别给出了群演化网络模型和KFDA的群结构更新模型对群结构的不确定性估计。群结构的不确定性估计是将群的结构Gt作为目标状态的一部分，形成扩展状态（X t，Gt），然后通过每个粒子包含的目标状态信息来估计对应的群结构，再将粒子的权重作为对应群结构的出现概率［8-9］。群结构估计图给出了估计群结构的概率分布，提供了群结构出现的概率信息，可以更好地反映出群结构内在的变化趋势。对比图10～图12可以看出，两种模型对于群结构的不确定性估计都基本符合真实群结构，可以给出群结构估计的概率，给定时刻颜色越接近红色说明对该种群结构估计的概率越大。图9～图11中纵坐标所对应的群结构如表2所示。其中，索引1，3，5为真实的群结构划分，其余为实验中出现概率较高的错误群结构划分，例如表中G5＝｛（1，3，8），（2，4），（5，6），7｝即为一种错误群结构，在真实的群演化中并未出现，但在估计中是有一定概率出现的，其真实群结构应为G3＝｛（1，3，8），（2，4），（5，6，7）｝，出现类似错误的原因一方面是因为杂波影响，使滤波结果产生误差，对群结构估计结果产生了影响，另一方面是由于模型的分群阈值并不能很好地适应全局，使一个群的目标被分为两个或者多个群。对比图11与图12可以看出，两者都出现了错误的群结构划分，但基于核Fisher判别的群结构更新模型比群演化网络模型对于群结构的不确定性估计要更准确，出现错误群结构的概率也要小于群演化网络模型，说明通过数据训练出的KFDA群结构模型比群演化网络模型全局适应能力更强。

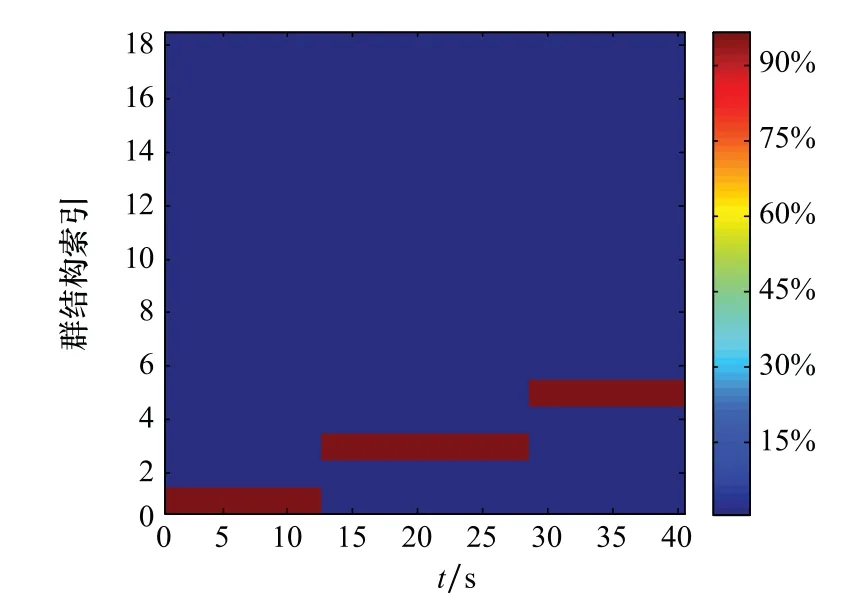
图10 真实群结构Fig.10 True group structure

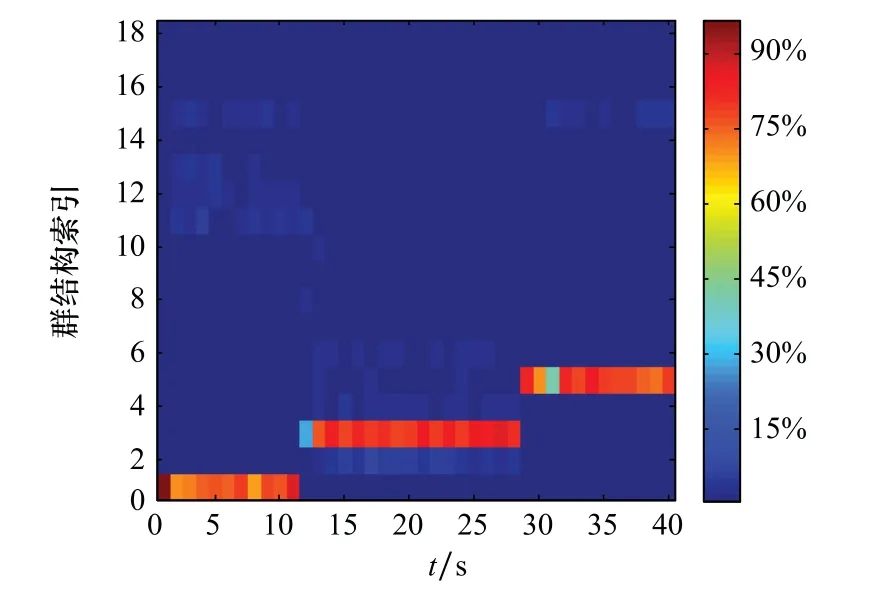
图11 群演化网络模型对群结构的不确定性估计Fig.11 Uncertainty estimation of group structure by group evolution network model

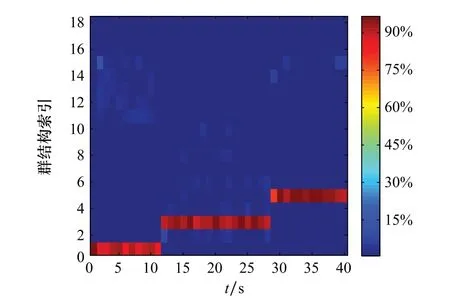
图12 KFDA群结构更新模型对群结构的不确定性估计Fig.12 Uncertainty estimation of group structure by KFDA group structure update model

表2 群结构库Table 2 Group structure library

续表2Continued Table 2

5 结 论

本文将群目标跟踪中分群的问题看作一个二分类问题，提出了一种KFDA的群结构更新模型，并基于该模型采用箱粒子PHD滤波实现了群目标的跟踪，仿真实验验证了本文所提模型的有效性。其对群数目的估计更为准确，模型训练后可直接使用，相比群演化网络模型效率更高，全局适应能力更强。随着机器学习的发展，将机器学习算法的一些理论和思想引入到目标跟踪领域，可以帮助解决一些实际目标跟踪中所遇到的问题。