深度信念网络算法下的热连轧板凸度预测模型
2022-10-09郝学斌
郝学斌
(河钢集团 邯钢公司邯宝热轧厂, 河北 邯郸056003)
板带钢板形是判断带钢质量好坏的重要指标之一.板形控制在生产过程中涉及轧制工艺、机械和控制等多个领域,如何实现高精度、高效率的板形控制成为这些领域研究者不断探索的研究方向[1-3].由于板形执行机构数量多、控制变量复杂以及板形执行机构与检测装置之间存在延时性,使得板形控制比厚度控制更加复杂,无论是引进的还是自主集成的自动化系统,均存在不同程度的板形控制稳定性差的现象.在规格切换、钢种切换和换辊后首卷等非稳态条件下的带钢,其板形控制精度无法单纯地通过改变轧制工艺和轧制设备来改善,因此,对非稳态轧制过程中的现场数据和控制机理模型进行分析、优化是板带热轧过程中亟待解决的热点问题.
在非稳态轧制过程中,带钢容易产生不均匀变形而出现浪形和头尾翘曲等板形缺陷,这会加大板形控制的难度,严重影响产品质量,大大降低板材的成材率.王建辉等[4]利用粒子群优化算法,并用适应度方差对适应度函数进行了改善,根据负荷分配优化策略,给出的目标函数具有了板形和板厚的最小方差,对精轧机组负荷分配进行了优化,板形质量得到了改善.段建辉等[5]研究了非稳态轧制过程中温度、速度、张力等参量对带钢厚度的影响,利用神经网络建立了非稳态轧制过程中厚度预测模型.为解决停轧换辊后非稳态轧制过程中带钢三维尺寸以及板形质量都比较差的问题,彭文、张殿华等[6-7]为轧辊磨损、热凸度、热膨胀等设计了新概念模型,对辊缝方程进行了改进.
上述研究均未涉及规格切换、钢种切换和换辊后首卷等非稳态条件下的带钢板凸度控制问题.因此,本文中依托邯钢公司邯宝热轧厂2 250 mm热连轧生产数据,考虑非稳态轧制过程中影响板凸度的相关因素,基于深度信念网络建立了板凸度预测模型,提高了非稳态轧制过程中的板凸度预测精度.
1 板凸度预测模型设计
1.1 深度信念网络算法
人工神经网络可以逼近任意非线性函数,对复杂系统的不确定因素具有很强的适应性和自学习能力,这使它在板凸度预测与控制中得到广泛应用.但浅层的神经网络在数据维数爆炸或非线性函数过于繁杂的情况下拟合能力较差,而非稳态轧制过程受规格切换、停轧换辊等因素影响,现场工艺模型预测偏差明显增大.为解决以上问题,本文中采用受限玻尔兹曼机建立规格切换和停轧换辊两种非稳态轧制过程的板凸度预测模型.
受限玻尔兹曼机( restricted Boltzmann machine,RBM)是基于玻尔兹曼机的一种特殊拓扑结构.在结构上,相对于BM,RBM 相邻层的节点相互之间全连接,而同层内的节点无连接,如图1 所示.

图1 受限玻尔兹曼机结构Fig.1 Restricted Boltzmann machine structure
受限玻尔兹曼机与神经网络类似,可见层和隐含层中的所有神经元均为二元分布,神经元取值为0 时表示抑制状态,取值为1 时表示激活状态,此时可见层单元和隐含层单元之间的分布为任意的指数分布.假设可见层节点数为n,隐含层节点数为m,则可见层向量?=(v1,v2…vn)T,隐含层向量=(h1,h2…hm)T.对于给定的一组状态,RBM 的能量公式可以定义为

式中:θ={wij,ai,bj},是RBM 内的参数集合;wij为可见层内第i 个神经元与隐含层内第j 个神经元的连接权值;ai为可见层内第i 个神经元的偏置;bj为隐含层内第j 个神经元的偏置.基于这个能量函数,可以得出这组状态的联合概率:
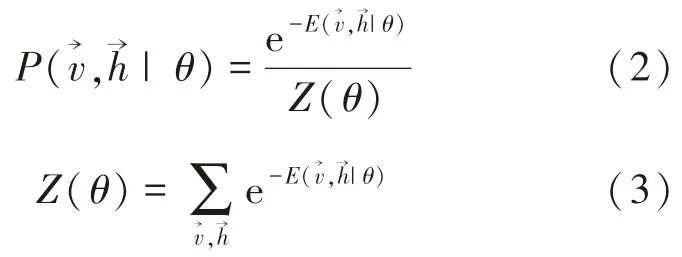

由RBM 的结构性质可知,同层内的神经元相互独立,故各自的激活也互不影响.当RBM 输入向量为、输出层第j 个神经元的值为1 时,该神经元的激活条件概率如下:

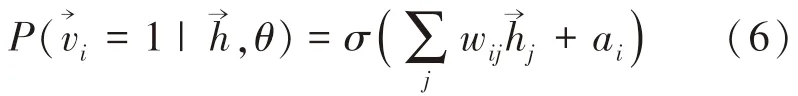
受限玻尔兹曼机学习算法的学习过程是无监督学习,目的就是将P(|θ)作为参数θ 的似然函数,在给定的无标签训练数据下,通过学习逐个样本调整θ 的值,使得P(|θ)值更大;大量的训练样本完成以后,输入训练样本数据集中提取的特征可以被视为输出分布.RBM 可以被视为一个浅层的神经网络,是许多深层神经网络的基本模块,在深度学习领域中被视为一个简单的生成式训练模型.
深度信念网络(deep belief network,DBN)是由多个RBM 堆叠而成的,包括一个输入层和一个输出层以及多个隐含层.根据无监督逐层学习特征的核心思想,低层输出作为高层的输入,每个RBM 的输入层节点数等于前面RBM 的隐含层节点数,如图2 所示.连接方式包括前两层间的无向对称连接和底层间的有向连接,第二层一般由第一层的回归机或分类器组成,再由自上而下的生成权值来确定各层之间的有向连接.
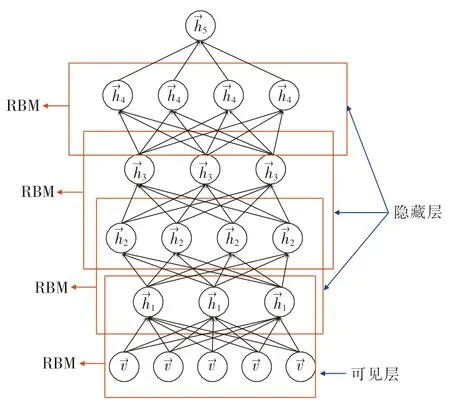
图2 深度信念网络结构Fig.2 Deep belief network structure
预训练过程中用输入数据训练第一层RBM,并以此状态输出作为第二层RBM 的输入并对第二层RBM 进行训练,这样依次训练,直到顶层.预训练使深度学习问题简化为多个RBM 的分层训练问题,化繁为简;同时,采用无监督贪婪地逐层学习到的网络权参数作为网络的初始化值,避免了权值参数陷入局部最优且加快了初始化速度,最终提升了训练的效果.在训练完所有的RBM 之后,可以再采用全局学习算法(例如反向传播)对网络进行微调,使网络达到最优.通过以上方法得到的DBN 模型就是提取高级特征的模型,对模型提取出的高级特征进行处理,能够精准预测出带钢板凸度.
1.2 板凸度预测模型的构建流程
先从现场采集的数据中挑选出非稳态轧制的数据,将其划分为训练样本数据和测试样本数据,再将训练样本数据划分为有标签数据和无标签数据.首先,将无标签样本数据用于模型自下而上的无监督预训练;其次,用有标签样本数据对模型进行自上而下的有监督参数微调;最后,用测试样本对模型进行测试.图3 为预测模型的整个构建过程.

图3 板凸度预测模型的构建过程Fig.3 The construction process of crown prediction model
具体的建模步骤如下所示.
步骤1:为了消除厚度、温度、轧制力等指标之间的量级差别对预测模型训练和测试的影响,本研究中对原始数据进行归一化处理,使数据范围在[0,1]之间.归一化的公式为
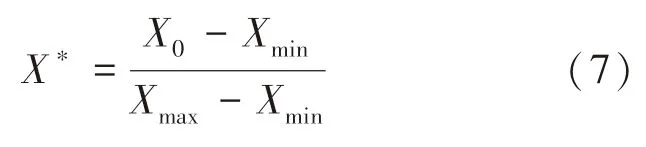
式中:X0为原始数据;X*为归一化值;Xmax,Xmin分别为输入数据的最大值和最小值.
步骤2:从大量的实际生产数据中,针对规格切换、停轧换辊两种非稳态轧制分别选取1 000个样本,其中700 个作为训练样本,300 个作为测试样本.再将训练样本分为有标签训练样本和无标签训练样本,无标签训练样本只输入数据,从有标签训练样本和测试数据中选取输入向量(非稳态过程中各扰动向量)和输出向量(带钢板凸度).
步骤3:利用无标签训练样本按自下而上的方式进行模型预训练.对于第k 层,其参数空间(wk,bk)由第(k-1)层的数据作为输入,再通过第k 层的数据对第(k-1)层的参数进行训练.各层神经元的激活概率根据式(8)和(9)计算,根据式(10)实现权值的更新:


步骤4:经过预训练后,利用有标签的训练样本,按自上而下的方式,以平方重构误差作为目标函数,采用梯度下降法对DBN 模型进行调整.
步骤5:将测试样本输入调整后的DBN 模型中,输出测试数据,并将测试数据反归一化得到完整的板凸度预测值.
步骤6:对比测试样本数据中的输出向量和步骤5 中得到的板凸度预测值,采用预测平均准确率等指标衡量DBN 模型的预测性能.
1.3 板凸度预测模型的输入和输出
本文中预测模型的输入变量就是非稳态轧制过程中影响板凸度的指标因素.为了最大化提取非稳态轧制过程中原始数据的特征以提高预测模型的精度,需要构建好规格切换、停轧换辊两种预测模型的输入向量,具体如表1 所列.
由表1 中可以看出:轧制力、弯辊力、温度等影响稳态轧制过程中板凸度的因素包含在两种预测模型的输入向量中;表1 中的x29~x36体现了硬度和尺寸的改变对规格切换、停轧换辊等非稳态轧制过程中板凸度的扰动.
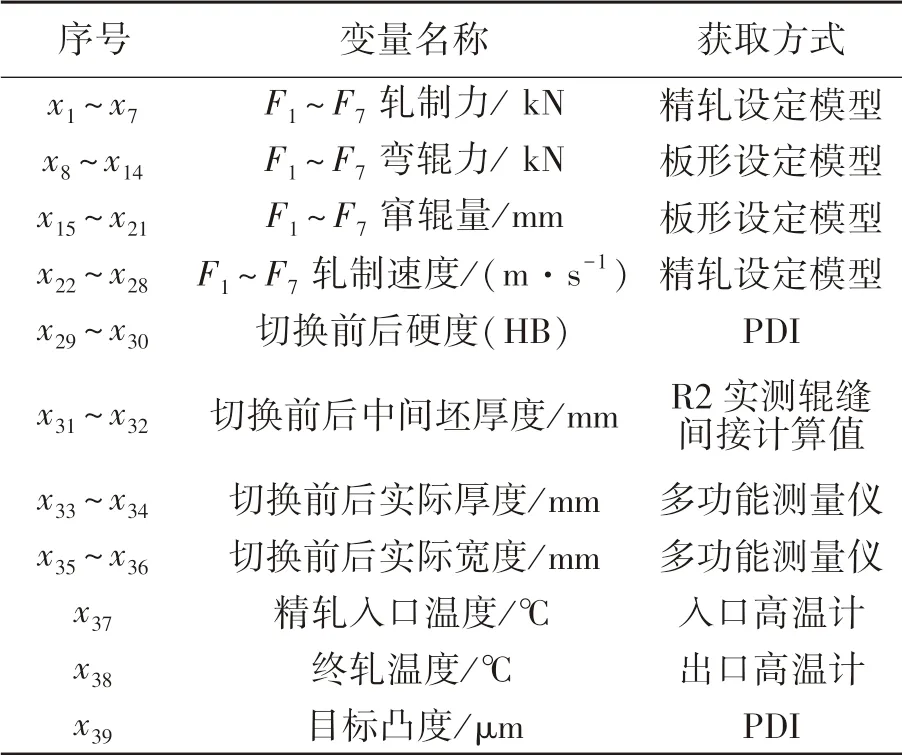
表1 非稳态轧制预测模型的输入Table 1 Input of specification switching prediction model
1.4 板凸度预测模型性能评价标准
在测试过程中需要根据性能度量对模型的准确性、可靠性进行优劣评价.本文中采用平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为模型预测效果的评价标准:
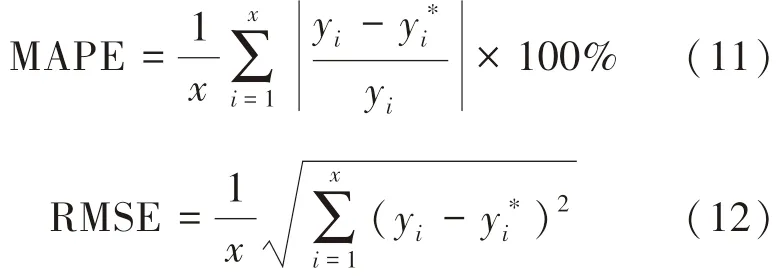
式中:yi为实测值;y*i 为预测值;x 为测试集样本数.
MAPE 和RMSE 越小,表明模型的预测值与实测值越接近,预测精度越高;反之表明模型的预测精度低.
2 深度信念网络算法下的板凸度预测
深度信念网络的设计是影响预测模型特征提取能力和预测精度的关键因素,包括网络结构的深度(隐含层层数)和宽度(各隐含层的节点数),以及各个节点的权重及偏置量等.
一般而言,网络中的层次越多,从输入数据中挖掘数据本质特征的能力就越强,算法的运算精度也就越高.但是随着网络层数的增加,结构也会变得越来越复杂,而网络计算耗时越长,越有可能出现累积误差,从而对预测的结果造成影响.到目前为止,并没有具体的理论可以确定深度学习的网络结构.本文中采用单一变量法,通过模型训练时发现,将无监督学习的动量和学习率分别设置为0.9和0.1 时训练效果最佳,RMB 内部迭代次数为100次,有监督学习的迭代次数为200 次,训练样本数为700 个,测试样本数为300 个.首先,确定输入层和输出层的单元个数分别为输入向量和输出向量的维数,设置每层隐含层的节点数均为10 个,隐含层的层数从1 层至6 层依次叠加变化;构建6 个DBN 模型进行仿真实验A1,将这6 个模型分别定义为Depth-1,Depth-2,Depth-3,Depth-4,Depth-5 和Depth-6.其次,将训练样本数从50 个开始以步长为50 增加至700 个,分别对6 个模型进行训练.最后,比较测试结果的MAPE 和RMSE 以确定最佳隐含层层数,结果见图4、图5 和表2.
由图4、图5 和表2 中可以看出,随着隐含层层数的增加,MAPE 和RMSE 先减小后增加,在层数为5 层时达到最小值.因此,将隐含层最佳层数确定为5 层.
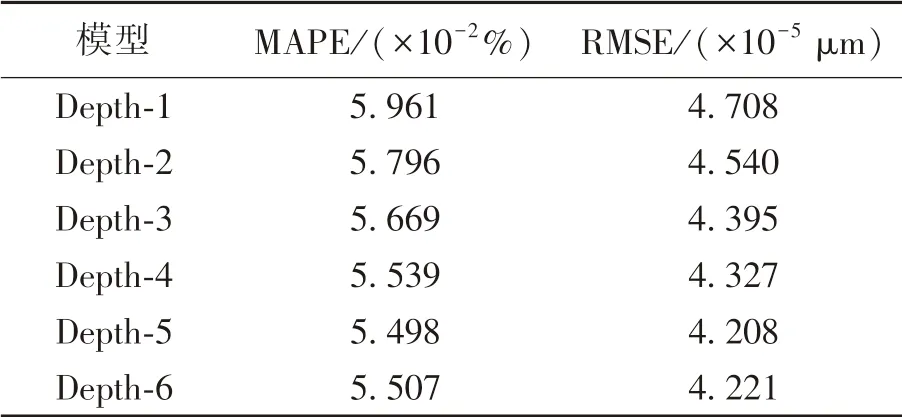
表2 A1 的结果数据Table 2 Result data of A1

图4 A1 的MAPEFig.4 MAPE of A1
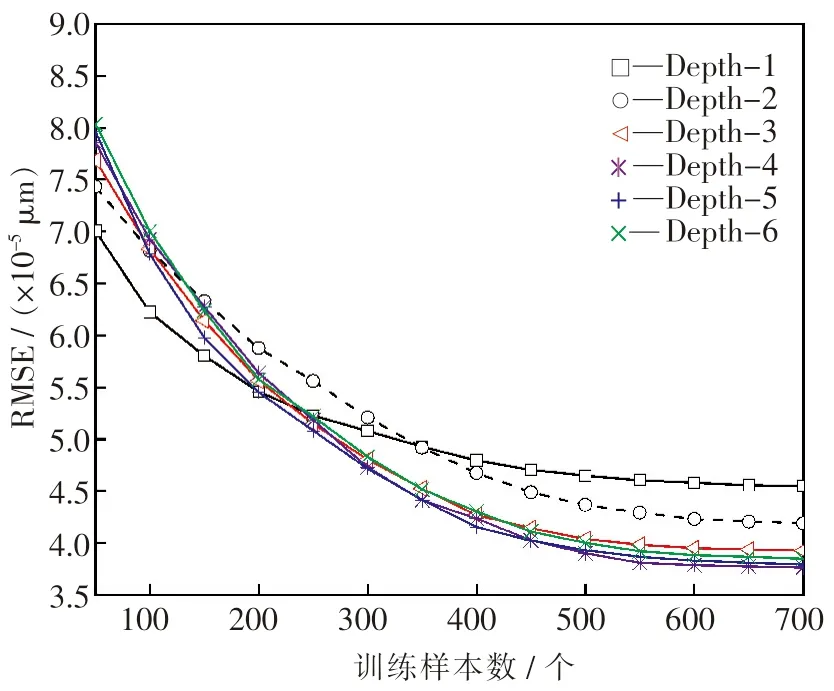
图5 A1 的RMSEFig.5 RMSE of A1
在确定了隐含层层数的情况下,隐含层节点个数的选择成为决定模型精度的关键环节.若隐含层节点数过少,则网络无法具备必要的学习能力和信息预测处理能力;反之,不仅会大大增加网络结构的复杂性,还会使网络在学习过程中更易陷入局部极小点,学习速度变得很慢.因此,根据经验,隐含层节点数的最小值取5 个,而最大值不应超过输入节点的个数,所以最大值取30 个.为比较每次网络训练的预测性能,采用的隐含层节点数按照步长为5 逐渐增加.因此,构建了隐含层节点数分别为5,10,15,20,25,30 个的6 个模型进行仿真实验A2,将6 个模型分别定义为Width-5,Width-10,Width-15,Width-20,Width-25 和Width-30.比较测试结果的MAPE 和RMSE 以确定最佳隐含层节点数,结果如图6 和图7 所示.
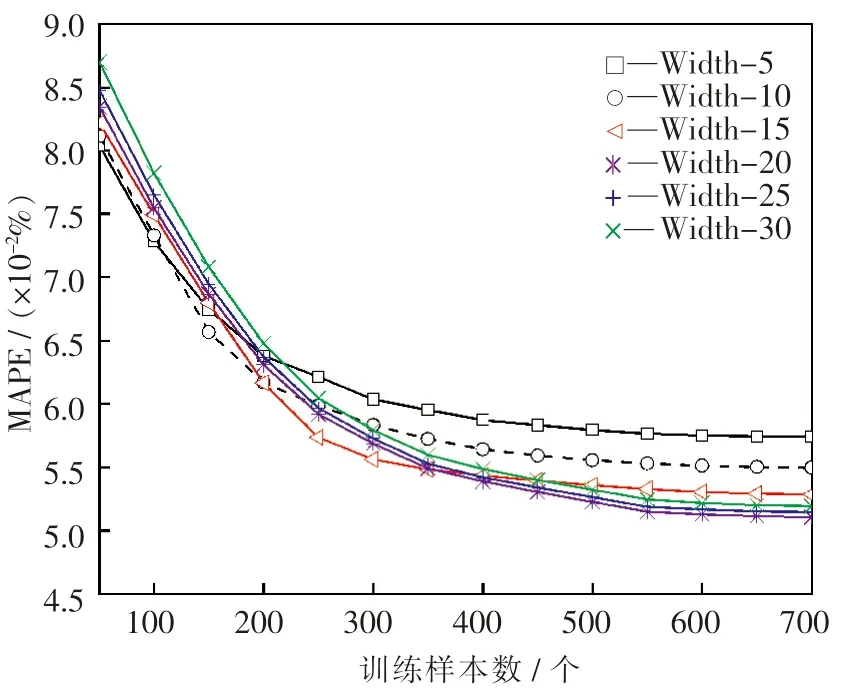
图6 A2 的MAPEFig.6 MAPE of A2
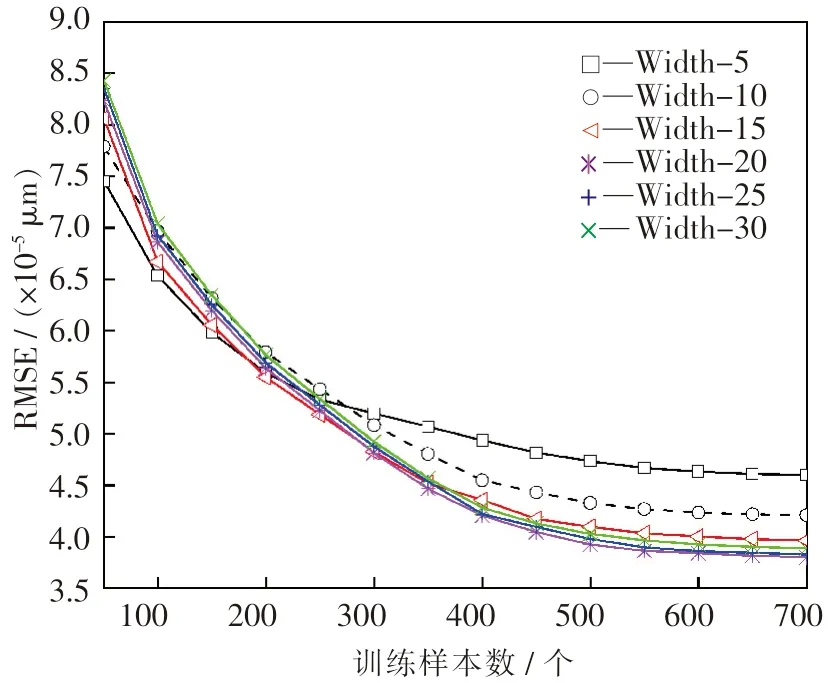
图7 A2 的RMSEFig.7 RMSE of A2
由图6 和图7 中可以看出,随着训练样本数的增加,MAPE 和RMSE 逐渐降低,隐含层节点数越少的模型MAPE 和RMSE 降低速率越快,越早趋于平缓,表明网络结构越简单、参数越少,训练速度越快,建模能力越强.当训练样本数达到700个时,预测模型的具体结果如表3 所列.

表3 A2 的结果数据Table 3 Result data of A2
由表3 可知,在一定范围内,随着隐含层内节点数的增加,模型的拟合程度越来越高,预测精度逐渐提高.需要注意的是,隐含层内节点数为20个的模型的MAPE 和RMSE 分别为(5.107×10-2)%和(3.805×10-5) μm,比隐含层内节点数为25 个和30 个的模型的MAPE 和RMSE 都要小,主要是因为较大的隐含层维度使得网络模型过于复杂,降低了建模能力和预测精度.因此,DBN 模型的隐含层节点数应选为20 个.
通过实验A1 和A2 可以得到规格切换和停轧换辊等非稳态条件下的预测模型DBN 的隐含层层数为5 层,隐含层节点数为20 个.为验证DBN 模型的性能,利用BP 神经网络建立了BP模型对板凸度进行了预测,隐含层层数设置为1层;通过多次实验对比,隐含层节点数设置为31个;采用梯度下降法的训练方式,迭代次数为200次.二者的预测数据如图8 所示,预测值与实际值的绝对误差如图9 所示.

图8 板凸度预测数据对比图Fig.8 Comparison curve of forecast data
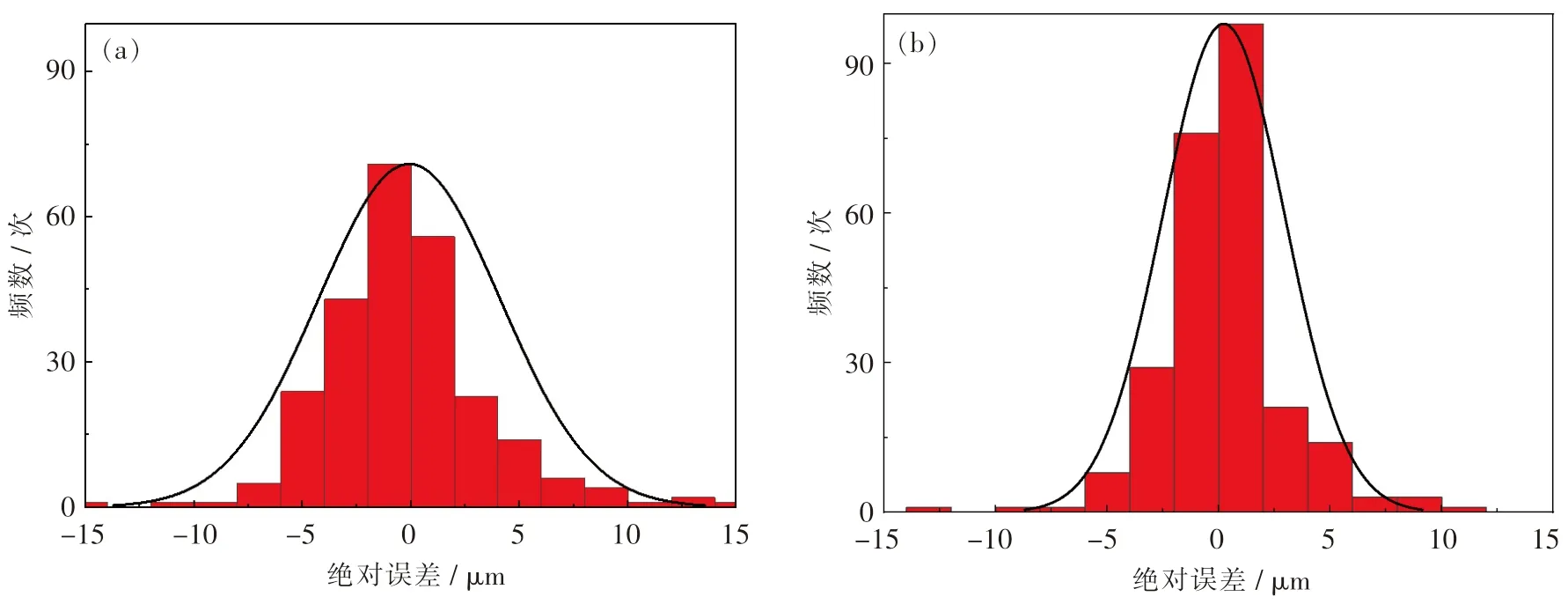
图9 模型预测误差柱状分布图Fig.9 Error histograms for prediction of proposed models
图8 为BP 模型及DBN 模型的板凸度实测值及预测值的散点分布图,实测值与预测值的绝对误差用颜色标度进行分级.当颜色从青色变为蓝色时,绝对误差从0 增加到10 μm,而红色表示绝对误差超过10 μm.两个模型的数据点都清晰地分布在y =x 两侧.DBN 模型的预测数据与实测值的绝对误差小于5 μm 的比例达到93.1%,且绝对误差超过10 μm 的样本数量更少.DBN 模型明显优于BP 模型.
图9 为两个模型的板凸度实测值与预测值的绝对误差分布柱状图,(a)(b)两张图的分布都近乎正态分布,形状上均中间高两边低,这表示绝对误差分布在x=0 两侧的样本数量较大.对于DBN模型,柱状图在x =0 两侧的样本数量明显比BP模型中的样本数量要多,即DBN 模型使得更多的样本有更小的绝对误差,也就说明了DBN 模型的预测性能更优.
图10 为两个模型的平均绝对误差(MAE),MAPE 和RMSE 的柱状比较图,可以此来综合评价模型的预测性能.与BP 模型相比,DBN 模型的MAE,MAPE 和RMSE 分别降低0.18 μm,0.5%和0.21 μm,为2.29 μm,4.98%和3.07 μm,预测性能明显更优.
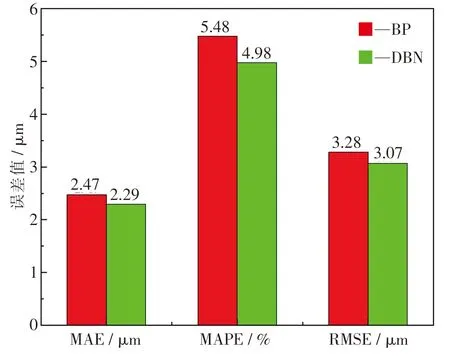
图10 误差值比较Fig.10 Error histogram comparison
3 结 论
(1)针对规格切换和停轧换辊两种非稳态轧制过程中板凸度预测的复杂问题,提出了一种深度学习的板凸度预测方法;设计了深度信念网络算法下的预测模型方案和建模流程,并选择出适合的模型评价分析指标.
(2)深度信念网络的隐含层节点数过少或过多时,会出现不同程度的欠拟合或过拟合问题,影响模型的预测性能.本文中通过对比实验来寻找深度信念网络(DBN)的最佳网络结构参数,确定了DBN 模型结构的隐含层层数为5 层、隐含层节点数为20 个时预测性能达到最佳.
(3) 与BP 模型相比,DBN 模型的MAE,MAPE 和RMSE 分别降低0.18 μm,0.5% 和0.21 μm,为2.29 μm,4.98%和3.07 μm,预测数据与实测值的绝对误差小于5 μm 的比例值达到93.1%,预测性能明显更优.
