一道2022年广东省一模试题的探究与推广

广东省中山纪念中学(528454)邓启龙

试题(2022年广东省一模第12题)已知抛物线C : y2= 4x的焦点为F,抛物线C上存在n个点P1,P2,···,Pn(n≥2,n∈N∗)满足∠P1FP2=∠P2FP3=···=∠Pn-1FPn=∠PnFP1=,则下列结论中正确的是( )

解析不妨设P1为x轴上方逆时针方向的第一个点,令∠P1Fx =θ,则θ∈(0,).

A. n = 2时, P1P2过F点,易得

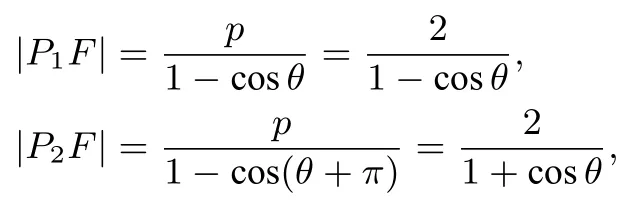
B. n = 3时,

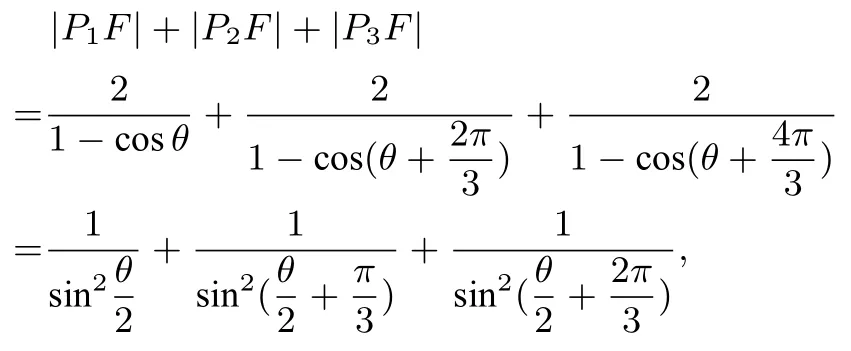
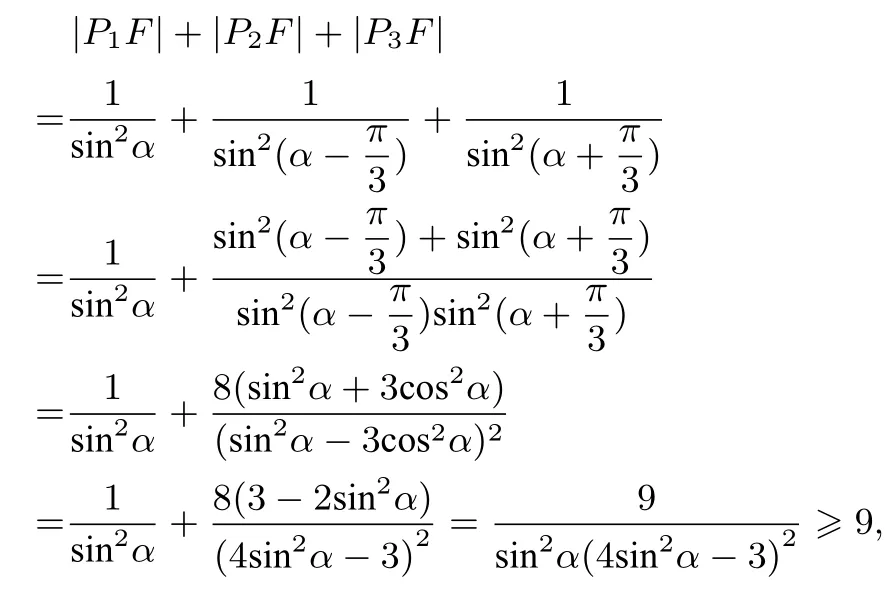
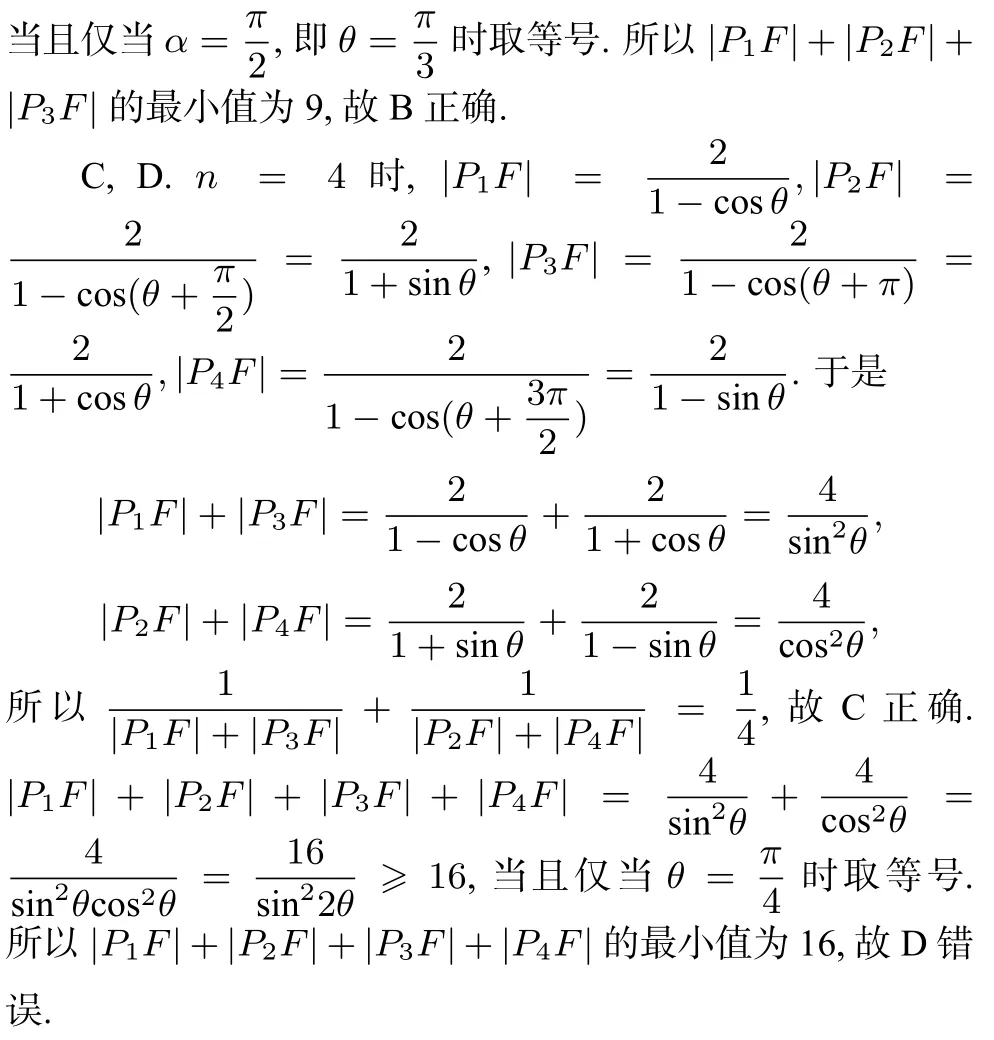
本文通过深入探究,得到了该试题的一般性结论.先给出本文要用到的两个引理.

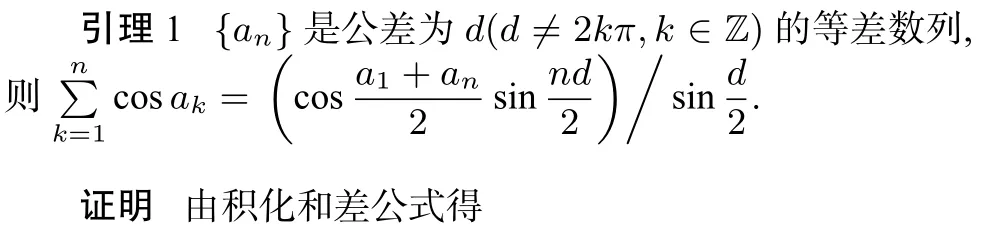
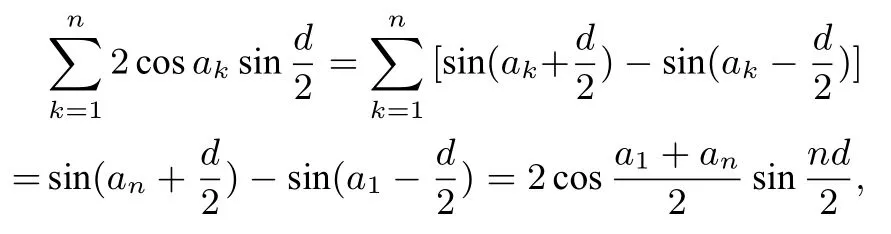
引理2

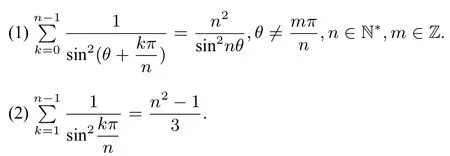
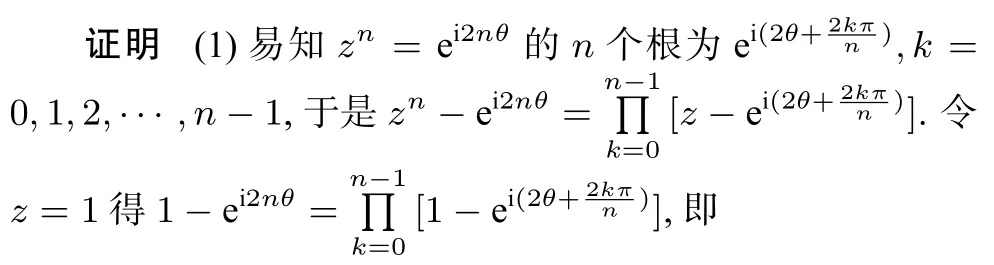
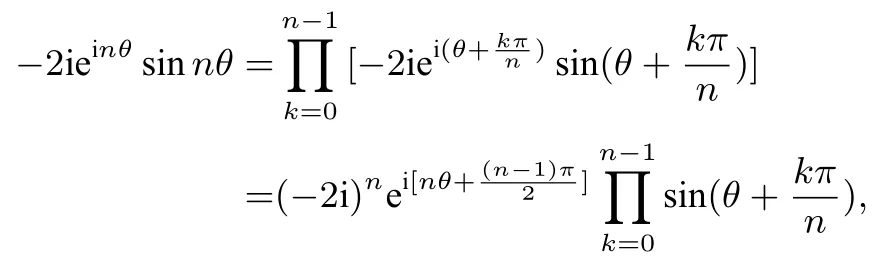
从而得到

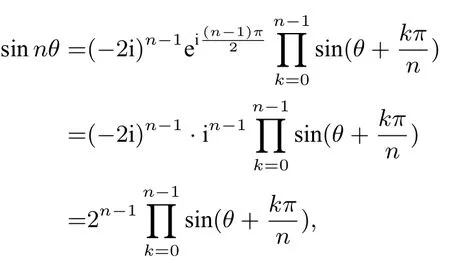
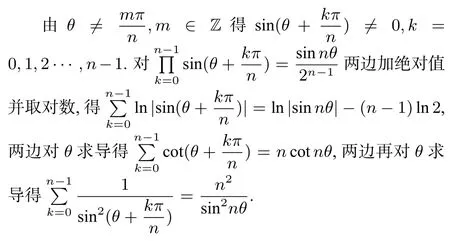
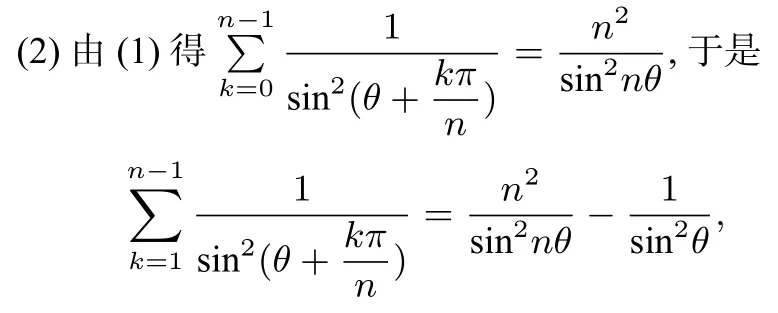
两边对θ取极限得

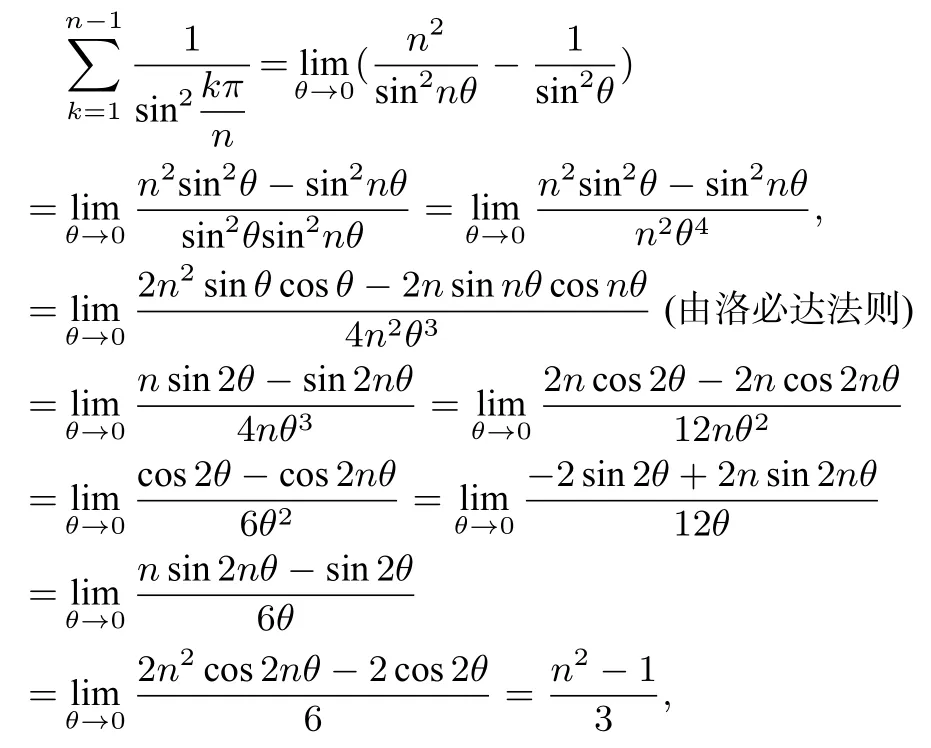
所以(2)成立..

接下来给出本文得到的一般性结论.

方法一由权方和不等式得

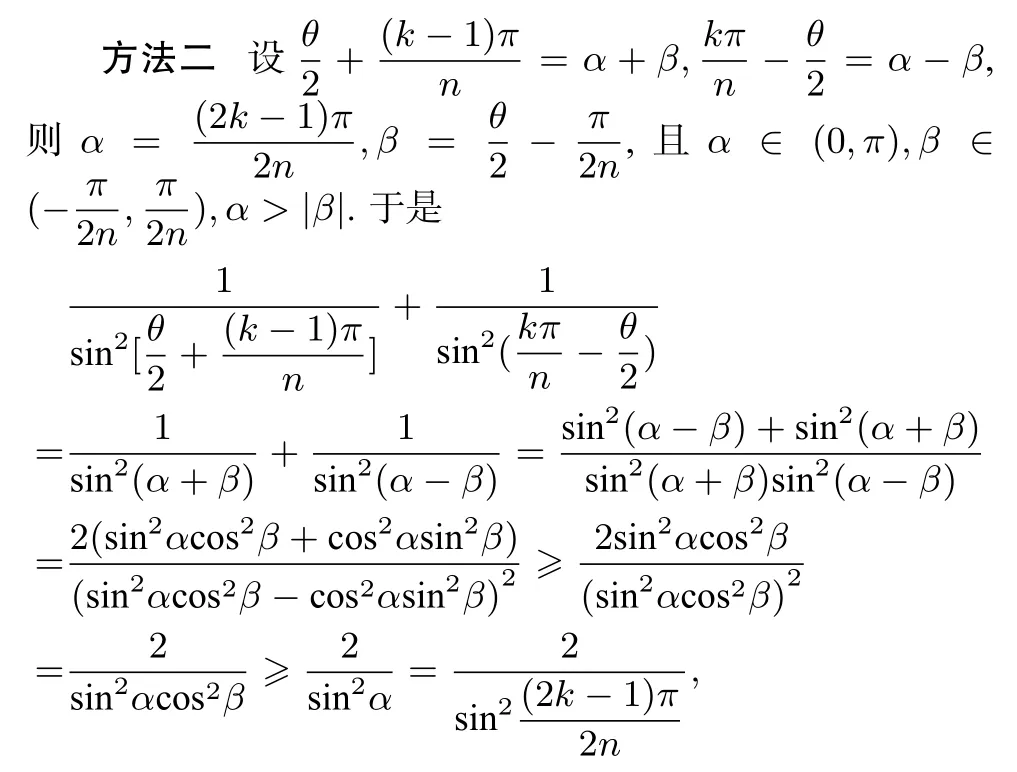
证明由引理2(1)得

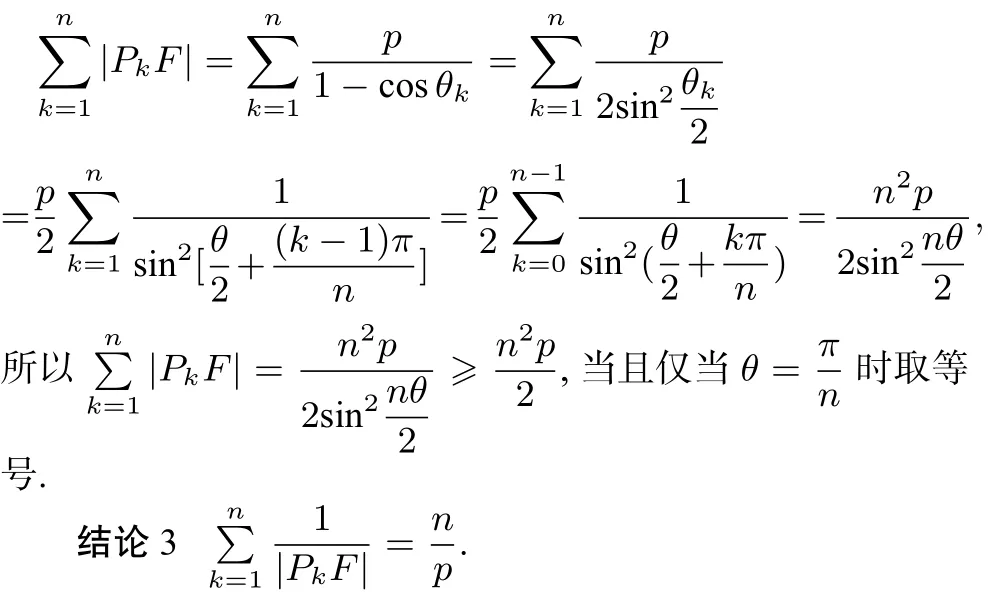
证明由引理1得

结论4当n为偶数且n≥4时,

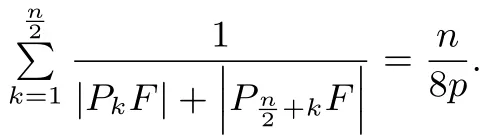
证明由引理1得