基于动态可视化软件GeoGebra的高中数学教育研究

广东省廉江市实验学校(524400)陈培锦

1 引言

在当今社会,数学学科已深入渗透到自然科学、基础物理、社会科学、金融管理等各个领域,发挥着举足轻重的作用,数学一直是中学教育中的重点学科.由于数学拥有高度抽象、可视性弱等特点,对学生的空间想象和逻辑思维要求高,其抽象性不可避免与中学生直观性思维观念发生冲突,是数学教育领域的主要难点和矛盾.如何化解这个矛盾,把不可视的数学知识和逻辑思维运用可视化的方式进行表达,一直是教育学者的研究方向.

赵然[1]结合自身教学经验,针对GeoGebra 软件在函数教学中的应用进行分析, 并成功在教学中应用, 实现了GeoGebra 在高效数学学习中的桥梁作用.张志勇[2]以“最佳口感茶水温度问题”为例,具体探讨了GeoGebra 在问题描述、模型建立、讨论求解等数学建模环节的具体应用; 刘蕾蕾[3]等以函数教学为例,阐述了如何将思维可视化,并应用可视化软件为学生的数学思维提供了形象化支撑依据.

本文基于GeoGebra 可视化软件,针对其在高中数学中的应用展开研究, 并分析其在高中数学课堂的实质性应用,评估其教学效果.

2 可视化动态数学软件GeoGebra 概述

2.1 软件介绍

GeoGebra 是一款轻量级、动态可视化、适合教与学的数学软件,于2001年由美国数学家Markus Hohenwarter 教授发明.GeoGebra 并非一款纯粹的绘图软件,除了拥有动态平面几何功能外,还有强大的代数运算、3D 绘图、概率统计、微分方程求解等能力,加上精美简洁的可视化界面,可胜任从数学启蒙教育到高等数学教育中所有的课程教学,辅助教育工作者进行数理分析、解决常见的数学问题等.

除此之外,GeoGebra 操作简便,上手门槛低,仅需具备基础的数学逻辑和知识.网页端、桌面端及移动端均可使用,其使用完全免费,不受任何相关因素的制约,能满足不同地区、不同层次学校师生教学的需要,已在多个国家数学教育领域成功进行应用.

2.2 主要功能及其应用

GeoGebra 软件在高中数学的主要应用有以下几个方面:

(1)在函数、导数、微积分等板块,教育工作者可以绘制函数图像,实现数形结合,并可通过动态调整参数,观察各个参数变化对函数图像的影响,辅助展示函数的单调性、奇偶性、极值、周期性和图像变换等特性,归纳各种函数的性质,加深学生对于函数解析式和图像构成的理解;

(2)在三角函数板块,运用GeoGebra 可以对三角函数进行动态展示,对于各类三角函数的相互关系、周期性、振幅、首相、最值等方面,都可以在软件界面进行动态平移伸缩进行变换,在教学时灵活切换,又不失一般性;

(3)在平面向量板块,可以通过软件对向量的概念及基本定理、坐标表示,以及向量的数量积、共线、垂直等几何意义,投影、夹角公式的推导等等方面进行详细讲解;

(4)在不等式板块,借助函数图像对数域进行直观的划分,通过数域的交叉组合以求得不等式值域,解决最值问题;

(5)在立体几何及解析几何板块,GeoGebra 可以进行一般性尺规绘图,以完全符合高中数学几何的绘图逻辑,快速精确绘制如垂线、角平分线、平行线等,实现绘图的严谨性,帮助学生掌握辅助线的绘制技巧; 同时可以旋转三维图像,以动画的形式在点线面空间关系方面给学生最为直观的展示,提高学生的空间想象能力;

解析几何方面,输入几何方程即可得到函数图像,同样可以通过各种参数的调整,参照对应的函数图像的变换,直观得到各参数在函数图像中的几何意义,对于直线与圆的相互位置关系、交点、距离等,该软件能够进行传统黑板绘图所实现不了的精确展示和动态变换; 另外通过绘制函数图像,可归纳圆锥曲线的基本性质,如顶点、焦点、长短轴、渐近线等,形象直观帮助学生进行曲线求解.

3 采用GeoGebra 软件进行解析实例

3.1 曼哈顿距离几何意义及方程图像

曼哈顿距离又称出租车距离,是衡量两个点在标准坐标系下沿两个坐标轴方向的距离Lx与Ly之和,曼哈顿距离T的计算公式为: T =Lx+Ly=|x1-x2|+|y1-y2|

其几何意义如图1 所示.

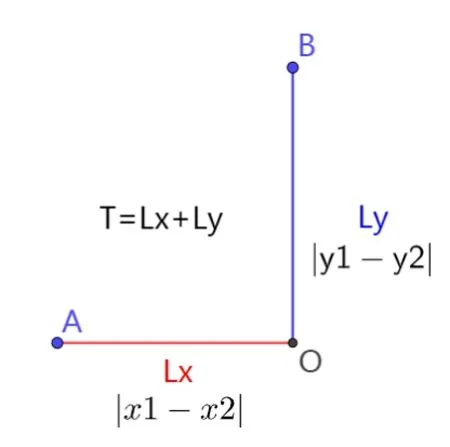
图1

设有定点P(1,3),则与点P 的曼哈顿距离T = 2 的点的方程解析式为: 2=|x-1|+|y-3|

该方程图像绘制如图2 所示.

图2

由方程图像可见到定点P 的曼哈顿距离T 的方程由4个分段函数组成,整体图像为正方形.通过解析式求得正方形一角点M 坐标为(1,1),可知角点至定点P 的距离(即对角线长度的一半)正好为曼哈顿距离T,是曼哈顿距离方程重要特性之一.

3.2 曼哈顿距离最值问题

曼哈顿距离衍生题型通常为求解某一曲线上的动点到给定点的曼哈顿距离最值问题.以椭圆方程为例, 应用GeoGebra 软件进行分析.

为保证一般性,在GeoGebra 软件中,设点P 的坐标为两个变量x0和y0,并通过变量滑动条控制点P 的位置.

在椭圆上找一个动点A,令点A 到定点P 的曼哈顿距离为T,通过在椭圆上移动点A,软件自动算出动点A 与定点P 的曼哈顿距离数值T,并赋值给曼哈顿方程变量T,即T = |x-x0|+|y-y0|,绘制出该曼哈顿距离方程,汇总得出的方程图像如图4 所示.

图3

可见动点A 恒为椭圆方程与曼哈顿距离方程图像的一个交点.此时通过软件移动点A,可鼓励学生观察点A 移动时,方程图像的正方形大小、边长和对角线长如何变化等.

显然,想要求得曼哈顿距离T 的最值,则需要正方形的对角线最长, 由于A 点同时在正方形和椭圆上,即两方程图像恒有交点A, 故当椭圆内切于正方形,且点A 为其中一个切点时,此时定点P距离正方形边线最远,对角线最长,即曼哈顿距离T 最大,如图4 所示.

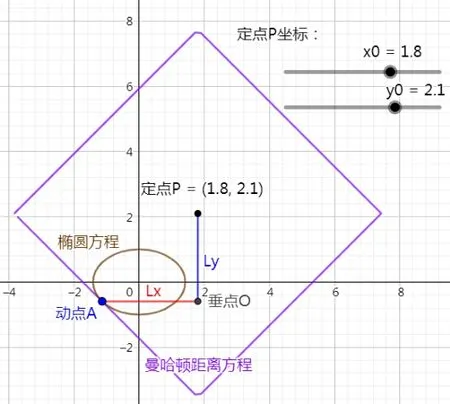
图4

应用该特性便可对T 的数值以及动点A 的位置展开进一步的求解.

在该问题的解析过程中,GeoGebra 软件能够实现各种显性或隐性的参数的联动,如定点P 位置、曼哈顿距离T、动点A 坐标等进行实时动态化绘图.并可通过动点A 在给定曲线的移动,以动画的形式展示动点A 与椭圆方程图像、曼哈顿距离方程图像的联动,拥有强大的直观可视性,有利于学生的观察和总结归纳.

需要注意的是,以上的推论仅探索了曼哈顿距离问题的一般特性,台州市2020年高二期末数学填空压轴题中定点P 是(1,0),椭圆方程为x2/2+y2=1,求该椭圆上动点至定点P 的曼哈顿距离最大值,有兴趣的读者可以进行研究,这里不再展开解析.

4 结语

GeoGebra 软件在数学教学方面的精确严谨、省时美观、参数互动等特性,同时内嵌的动画及动态绘图系统,能够方便学生更直观地学习数学抽象板块的知识点,培养图形思维,增强数形结合能力,发挥多媒体教学的优势,构建一个交互式现代化数学学习环境.