巧用微短视频,助力思维分享*——以“整式中的规律探究”教学为例

广州市增城区教师发展中心(511300)张河源

1 引言

微视频是按照课程标准的要求,将知识内容按学科逻辑与学生的认知特点划分为若干较小的知识模块,运用现代信息技术手段,整合图、文、声、像等元素制作成的便于学生学习的视频资源.一般泛指大小100 兆以内,播放时间几十秒到5 分钟左右,针对初中数学中的一个重点知识或认知难点进行精炼讲述的授课视频短片.

《朱子语类》收录了南宋教育家朱熹与其弟子的对话,在卷九“论知行”篇有“不可去名上理会,须求其所以然”;在其他卷中还有多处讨论“知其然”与“知其所以然”的关系,这是中国传统文化的精髓.我国当代数学教育家傅种孙先生的教育思想“理解数学知识的三重境界: 知其然,知其所以然,何由以知其所以然”,彰显了中国当代数学教育对传统文化的继承、发扬和光大,对笔者启发甚大.基此,笔者从“如何使学生想得到”上下功夫,执教了人教版七年级数学“整式中的规律探究”一课,灵活运用微短视频,精准搭建学生探究知识的思维桥梁,化解学生在探究知识的难点与痛点,在“知其所以然”上狠下功夫,收获良多.

2 微短视频,精设情境,激发兴趣

请同学们伸出左手, 一起做下面的游戏: 从大拇指开始,如图1 中显示的这只手那样依次数数字1,2,3,4,5, …,请问数字20 落在哪个手指上?

图1

你们能很快地说出数字200 落在哪个手指上吗? 2000呢?学习兴趣是影响学生学习效果的一个核心因素.学生只有对所学的内容产生了浓厚的兴趣,才能激发强烈的求知欲,进而享受学习的过程.

教师: 精心制作“数手指”的游戏视频并进行播放,让学生在真实的情境中,身临其境地感受游戏的全过程.学生在有趣实用的游戏中分析研究数学问题,有效激发学生对新知识的学习兴趣,充分调动学生内在的学习动机,使学生处于愤悱状态,全身心地投入学习活动中去,感受知识的生成.

上述课堂教学活动,彻底改变了以往让学生课前看的文字材料或多媒体材料不能引起学生的兴趣,得不到好的学习效果,从而导致课堂进行知识内化的失败的教学方式.微视频的使用能够代替教师进行知识传授的工具,并使翻转课堂成为广受欢迎的教学模式.

3 微短视频,探究问题,凸显思维

如图2,用火柴棒拼成一排由三角形组成的图形.如果图形中含有n 个三角形,需要多少根火柴棒? 你能想到多少种办法?

图2

本探究以具有内在逻辑关系的“问题链”,逐步展现如何由点、线、面,自然过渡到用整式表示图形的火柴棒数量,如剥洋葱般引导学生深入思考,凸显数学核心素养学习的思维之道,实现思维分享.

问题①我们知道一个三角形由三个顶点、三条边组成,那么如何将火柴棒拼成一个三角形?

设问意图: 确定一个三角形的要素: 三个点,三个线段.

问题②如果图形中含有2 个三角形,那么需要多少根火柴棒?

设问意图: 理解重叠图形中存在一条公共边.

问题③如果图形中含有3 或4 个三角形,那么需要多少根火柴棒? 可以用数量准确刻画吗?

设问意图: 理解重叠图形中存在公共边的条数与三角形个数之间的关系.

问题④如果图形中含有n 个三角形,需要多少根火柴棒? 可以用数量准确刻画吗?

设问意图: 基于初中学习经验, 学生容易猜想出结论“2n+1”,但是如何小心求证“结论”,再寻求思维上的突破,以下是课堂上的教学尝试.

教学片断1: 定量刻画三角形与火柴棒的探索.

教师追问1: 如何用三角形的个数来刻画“火柴棒”?

学生; 由特殊图形进行分析, 图形含一个三角形则有3根火柴棒,含两个三角形则有5 根火柴棒,含三个三角形则有7 根火柴棒,依次类推,含有n 个三角形则有(2n+1)根火柴棒.

教师追问2: 你有什么其他想法?

学生: 小组讨论,展示成果.

教师: 播放制作好的“学生讲课小视频”和“图形拆拼动画视频”,引导学生深入思考.

学生: 经过自主思考与小组交流后产生以下发现.

发现1: 用基本图形“三角形”加上增加的“火柴棒”,则有3+2(n-1)根火柴棒.

发现2: 基本图形“一条线段”加上增加的“火柴棒”,则有1+2n 根火柴棒.

发现3: 用“水平摆放的火柴棒”加上“倾斜摆放的火柴棒”,则有n+(n+1)根火柴棒.

发现4: 用“拆开后三角形的火柴棒”减去“拼合后重叠的火柴棒”,则有3n-(n-1)根火柴棒.

发现5: 图形规律转化为数字规律,利用数字解决问题.

上述课堂教学活动,学生从不同角度,通过观察、分析、探究、归纳,数形合一,启发学生基于旧有经验,突破思维局限,创新研究思路,完成探索推理,概括获得新知.这符合皮亚杰的认知发展理论: 学生在遇到新概念时,总是用现有认知结构去同化,如果获得成功,就得到暂时的平衡;否则,则会调节已有认知结构或重新建立新的认知结构,以顺应新概念,从而达到新的平衡[2].

4 微短视频,精研内涵,夯实迁移

认知心理学家认为: 在学习某个知识时,可能对所学知识有所拓展,有时甚至会做出某种推论,这个过程就是对知识“精致”的过程.在数学学习中,“精致”的实质就是对数学知识的内涵与外延进行尽量详细的“深加工”,以使学生建立更清晰的概念表象,获得更多的概念例证,对概念的细节把握得更准确,理解概念的各个方面,获得概念的某些限制条件等.这一“精致”过程通常表现为对各种可能的特例进行剖析,分析可能发生的概念理解错误,理解概念的各种变式等等[2].以下是本节课的教学尝试.

教学片断2:月历中的数学问题

问题⑤图3 是某月的月历.

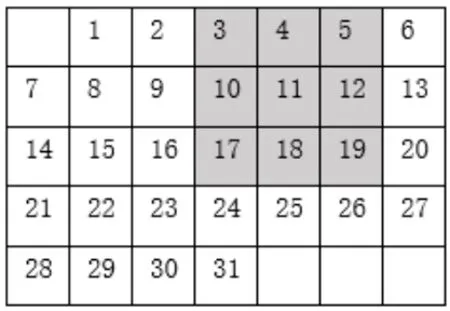
图3

教师: 带阴影的方框中的9 个数的和与方框正中心的数有什么关系?

学生: 方框内数字的和为99, 恰好是中间数字11 的9倍,因此,11 恰好是方框中9 个数的平均数.

教师追问1: 如果把带阴影的方框移至图4 的位置,上述关系还成立吗? 说明理由.

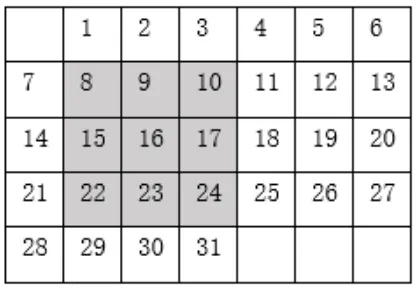
图4

学生: 移动后,方框内的数字和为144,恰好是中间数字16 的9 倍,因此,16 是方框中9 个数的平均数.

教师追问2: 不改变带阴景方框的大小,将方框移来参加几个位置试一试.

你能得出什么结论? 你能证明这个结论吗?

你能得出什么结论? 你能证明这个结论吗?

学生: 这个是普遍规律,证明如下,设中间的数为x,则其和为9x.

教师追问3: 这个结论对于任何一个月的月历都成立吗?

学生: 这个规律对任何一月都成立.

教师追问4: 如图5,如果带阴影的方框里的数是4 个,你能得出什么结论?

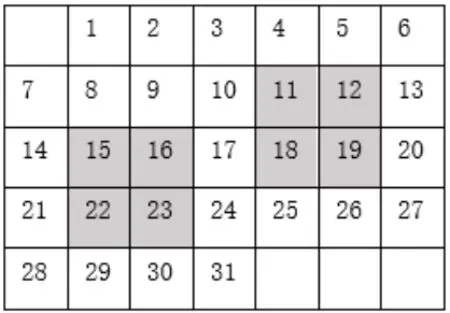
图5

学生: 对角线上两个数的和相等.15+23 = 16+22,11+19=18+12.

教师追问5: 如图6,对于带阴影的框中的4 个数,又能得出什么结论?

图6

学生: 对角线上的两个数字的和相等.18+13=12+19.

上述课堂教学活动中,教师通过播放教学微视频,教学微视频的设计针对学习者的学习特点设计相应的视频风格,通过吸引学生的注意力,高效完成知识的传授.教学视频作为一个提出问题、形成对话交流、为项目或实验提供指导的媒体工具,提供补习,提供案例或方法,并解决问题.学生是否能够完成教学视频的学习决定了知识传授的质量,对后续知识的内化起着至关重要的作用.学生通过具体分析与推理、讨论与辨析,进一步挖掘出带阴影方框中的数字的本质属性.这样,知识逻辑顺序的自然与思维过程的自然相结合,学生的思维之道得以顺利拓展,学生在课堂上有效实现思维的展示与分享,真正实现“知其所以然”.

教学片断3: 知识有效迁移

问题⑥按图7 方式摆放餐桌和椅子,照这样的方式继续排列餐桌,摆m 张桌子可坐多少人.

图7

问题⑦观察图8 并填表(单位: cm):

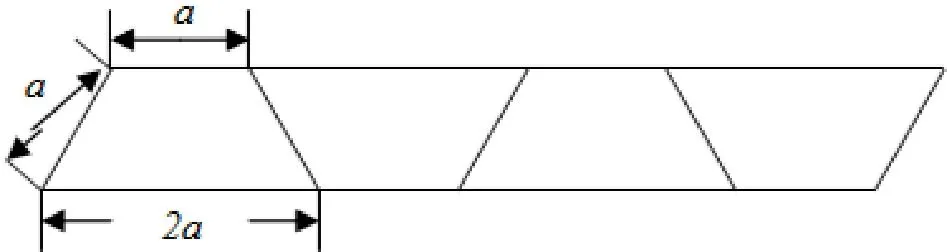
图8

本练习独到之处在于: 既重视“几何图形代数化”,又强调“代数式子几何化”;既提升了学生“直观想象”、“数学运算”、“逻辑推理”的核心素养,又渗透“数形结合”、“化归转化”的数学思想, 巩固新学知识, 进一步熟悉规律探究方法,培养学生独立思考和解决问题的能力.

总之,如何使学生想得到,如何让学生的思维活动自然展开,关键在于对数学知识本质的把握和对学生学情的深入理解.本节课承载着让学生初步体会数形合一思想的重任,而点、线是最简单的几何图形,规律性探究是简单但能很好地反映“用代数的方法刻画几何对象”的载体,因此,本节课不仅要有“交代问题背景、引入研究方法、构建研究蓝图”的整体构想,使学生感受到数形合一的基本特点,更要基于学生已有经验设计合理的思维之道,帮助体会到用数形合一法研究几何问题的基本套路(即“一般观念”),进而提高提出问题、研究问题的能力[1].