含参二元一次方程(组)有效教学的实践

广东省广州市第十六中学(510631)梁镇辉

1 含参方程组教与学的反思

含参方程组问题是学生学习的难点,又是教学不可绕开的重要教学内容.但是不能退化为“题型教学”.试图“穷尽题型”,幻想通过“题型”的机械重复、强化训练来提升学生对应的“技能”和“动作要领”,这种“刺激-反应-强化”的行为主义教学方式,让学生在“新情境”背景下变得意义不大.

刘钊秀、祝林华[1];彭翠华[5];李自刚,杜兴明[3]等归纳了常见的含参二元一次方程组的相关题型以及变式应用,总结了处理该类题目的一般方法和技巧.笔者以基本解题思路为依据将其重新归为3 类: 第1 类是‘知道方程的具体解代入方程’;第2 类是‘先重组方程求出具体解后代入’;第3 类是‘用含参数代数式表示方程组的解再代入’.教师和学生都认为这种含参方程组问题无论是初学还是对后续的学习而言都是一个难点.

孙桥[4]从知识层面和解决问题层面分析了学生的困惑所在.笔者经面批和访谈后发现学生的困惑主要有: 课堂上,学生不容易接受“参数方程组万能办法[5]”的解题思路;独立做题时,不容易区分到底如何“消元”,有的学生更是简单地对一个方程进行移项(例如x = 3y+m)就得到“含参表达式”;计算过程中,对繁琐的计算[5]存在“厌烦”的情感态度,部分学生情愿放弃.笔者在课堂观察中,发现大部分老师(包含文[1]至文[5])采取了“就题论题”的教学方式,把含参问题分成了一个个“类型”,然后对这个“类型”采取与之匹配的解题思路,而在“消元”办法的思考以及方法策略上少有介绍,课堂留下的是一种又一种解题思路的“惊讶”! 这种“教套路”的知识传授方式不能被学生很好理解(见下文测试效果数据).比如孙桥[4]在教学设计中尝试引导学生基于“消元”的思想解决问题,但是他介绍的一题多解,更多的还是方法和经验介绍,因为他以问题3 引入“用含参数的代数式表示x 和y”,再运用到其例题的解决上,难免“限制”了学生思维的发展,缺乏引导学生分析“消元”的策略.

2 含参方程组教与学的实践

下面笔者基于引导学生分析“消元”策略以及充分暴露“消元”思想,进行教学实践,并从调查问卷、测试等角度分析优良教学效果.

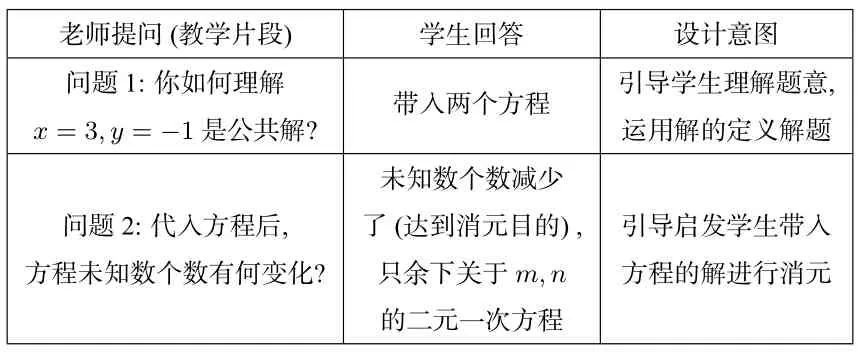
例题1已知是方程4x + my = 10 和mx-ny =11 的公共解,求m2+2n 的值.教学过程如下表:

?

《数学课程标准》中指出‘数学思想蕴含在数学知识的形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括,学生在积极参与教学活动的过程中,通过独立思考、合作交流, 逐步感悟数学思想.’例题1 把未知数x、y 的值代入方程就能达到消元目的,实际上这就是“二元一次方程”基本解法中的“代入消元法”.文[2]称之为对二元一次方程组的工具性理解.但是通过“问题串”启发学生:代值也是解决含参二元一次方程组问题的基本思路,就提升了学生对“消元”的本质理解,这促进了学生对例题2(重组方程组)以及例题3(用参数表示x 和y)的主动思考,作为解决含参方程组问题的“出发点”.

例题2

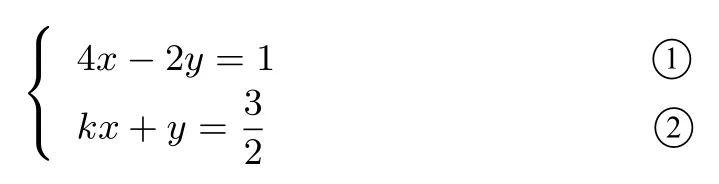
的解中,x 和y 的值相等,试求k 的值.教学过程如下表:

?

《标准》认为‘有效的数学学习活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的重要方式.’《标准》对‘数学理解’的解释是“能描述对象的特征和由来,能明确地阐述此对象与有关对象之间的区别与联系”.通过提问反思引导学生理解题意,从中发现各个方程的结构特征,理解“重组方程可消元”是解决上述问题的基本方法.

例题3当a 为何值时,方程组

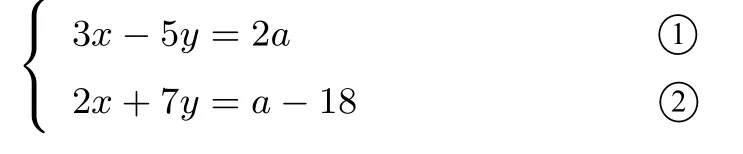
的解x,y 互为相反数? 教学过程如下表:

?

让课堂教学的一切来得顺其自然.《标准》的基本理念认为‘数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上’.立足学生对消元的已有认知,才能经过数学提问启发学生找到“消参法”;充分认识了“代入消元法”后,学生对“用含参代数式表示x 和y”才容易释然;把握住“消元本质”,学生才能从消元角度进行解法发散,才能想到思路一、思路二、思路四[4].

3 含参方程组教与学的效果分析

?

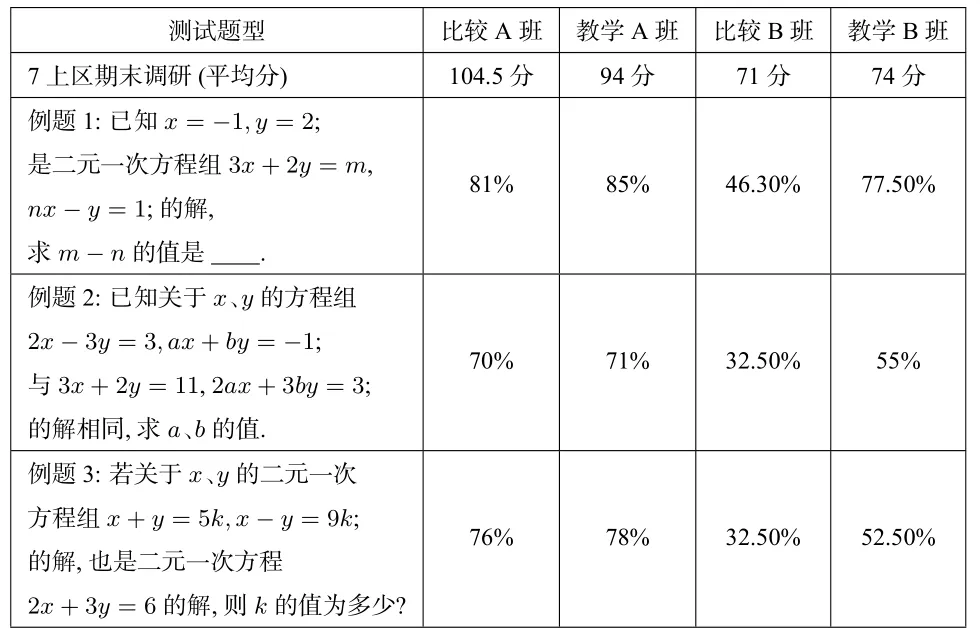
从上表可以看到教学效果显著.教学A 班与比较A 班学习能力相差较大,而测试题的答对率均超越比较A 班;教学B 班与教学A 班学习能力差距更大,但答对率比较接近教学A 班;在同层次班级中,教学B 班的答对率明显比比较B班高出20 个百分点.

从上表可以看到“题型教学”效果差.测试题目与课堂例题均存在表达差异.细看学生答卷情况,可以发现比较B 班“不理解题意或者没有解题思路”的学生显著多于教学B 班的情况,同时教学B 班答错的学生当中,多是在解方程组中“出现计算错误”,但是解题思路完全正确.而A 层次的两个班级,错误学生出现的情况主要为计算错误.显然突出“消元本质”的教学效果有效训练学生数学思维,但是不能保证学生计算准确性.

从学生解法呈现结果看,抓住数学本质的教学有利学生“创新性理解[2]”.从答对的学生中,笔者的两个教学班,在解法上呈现多样性.例如对测试例题3 的消元办法有的是联立已知方程组消参;有的是利用已知方程组用含参代数式表示x 和y;有的是先利用整体代入消除‘x+y’得y 与k 的关系;有的是转化为三元一次方程组再消元;有的找到三个方程的数量关系转化为关于k 的一元一次方程.可见学生对该类问题有很好的‘解法创新’[2].相比之下,两个比较班在解法上比较单一,大部分学生采取用含参数表示x 和y 的办法解决问题.

从课堂教学看,突出思维过程的教学有效激发学生学习兴趣.《标准》指出“使学生获得对数学理解的同时,在思维能力、情感态度与价值观等多方面得到进步和发展.”笔者教学班的学生争抢上台“表演”,思维活跃.布鲁纳认为“学习的最好刺激乃是对所学知识的兴趣”.本届学生的特征是喜欢走上讲台来表现自己,让学生多讲,老师扮演倾听的角色,这正是刺激学生学习数学兴趣的好办法.

4 教学反思

对学生而言,想达到对知识的创新性理解[2],就要注意创新性理解的起点是要能够清晰而准确地把握数学对象的本质.初学这种“含参方程组”问题时,学生的感受是“香菇难受”.学生会解具体系数的方程组,也容易掌握“(重组方程)求解后代入”的办法解题,但是遇到常数项为参数的问题就顿生困难了.‘这种情况好比一个人已经学会了骑单车,但是现在要让他骑摩托车一样’,这就需要学生改变自己对方程组特点的主体认识,把握“消元”的数学本质,来适应这种含参的方程组,达到消元认识的质性提高.

教学要抓住数学本质的知识,抓住一两个前后一致、贯穿课堂始末的数学思想主线,做好“数学提问”,让学生深入理解数学概念和思想方法,再进行解题操作,这样才容易培养学生的数学“根基”.如果对含参方程组的教学仅仅停留在一题多解,通过多种方法来说明消元思想,最终不过是让学生“饱了眼福”.我们在教学过程中,更应该让学生体会到“纸上得来终觉浅,绝知此事要躬行”的学习道理,让学生围绕‘消元思想’进行头脑风暴,自主探索并归纳出消元的不同解法.