初中几何中三角形等面积法的应用探究

广东省珠海市第五中学(519000)韩 彬

三角形的面积公式为: 底与高乘积的一半.看似非常简单,小学便已掌握.在我们深入研究了公式本质后,发现“等底同高”,“等底等高”,“同底等高”的三角形面积都相等.对于不同的两个三角形来说,无论底和高的位置如何变化,只要长度数值不变,乘积就不变,面积也不变.对于某一个确定的三角形来说,即便是改变底和高,由于研究的对象没变,面积也不会改变.因此三角形的面积相等将会有很多种可能.当我们把它灵活的运用起来以后便可以巧妙的解决求线段长,求图形的面积,求最值,证明存在性等问题.

1 构造三角形中线,寻找面积相等的三角形

人教版八年级上数学课本,对于三角形的中线的定义是这样的.如图,连接ΔABC 的顶点A 和它的对边BC 的中点D,所得的线段AD 叫做ΔABC 的边BC 上的中线.

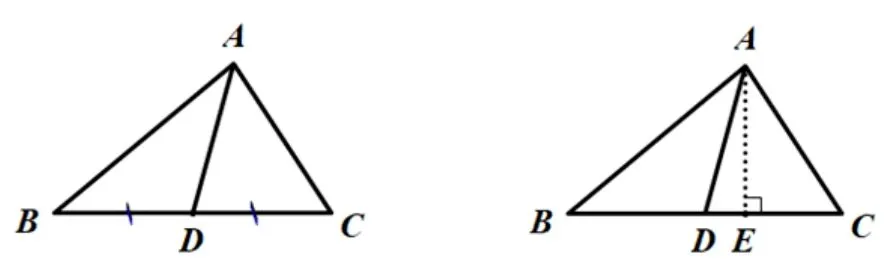
图1

例1长方形ABCD 的长为a,宽为b,E,F 分别是BC和CD 的中点, DE,BF 交于点G, 求四边形ABGD 的面积.

小结该题是一道相对比较复杂的几何题,题目没有给具体的数据,只表示出了长方形的长和宽,而四边形又是一个不规则的四边形,没有面积公式可以利用.解决这题的唯一抓手就是充分利用好边的中点.中点产生中线,中线分两个等底同高的三角形,因此就将这道题串联起来了.利用中线将四边形的图形进行分割,产生三角形,再利用三角形的等面积的性质,将三角形的面积进行等量转换,从而表示出每一个小三角形的面积,才能得解.

2 巧作一组平行线,发掘面积相等的三角形

例2如图,在4×4 方格纸中,小正方形的边长为1,点A,B,C 在格点上,若ΔABC 的面积为2,则满足条件的点C 的个数是____.

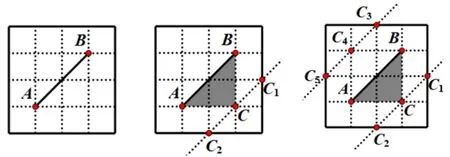
图3

分析本题是一道难度适中的填空题,其实网格中除去A,B,C 三点之外的格点并不多,采用枚举法也可以找出答案,但是比较繁琐.我们可以过C 点作直线AB 的平行线,平行线上的所有的点都可以满足与AB 构成的三角形面积等于2.同时关于直线AB 对称的位置也还会有相等数量的点.

解答过C 点作直线AB 的平行线, 与方格线交于C1,C2两点,连接C1A,C1B 得出ΔABC1,因为SΔABC1=SΔABC,同理可得: SΔABC2= SΔABC,根据图形的对称性,在直线AB 的另一侧对称的位置也会有一条平行线,与方格纸会产生C3,C4,C5三个点.所以满足条件的点有5 个.

小结解决本题,不需要通过计算,而是借助平行线巧妙的去构造多个同底等高的三角形.利用同底等高的三角形面积相等的特性来解决问题.在寻找同底等高的三角形时,最关键的步骤是利用平行线,平行线与网格线的交点便是符合题意的点.本题充分的体现了等面积法所带来的快捷性和准确性.结合平行线利用等面积法解题对于函数图形问题还有更加重要的作用.

例3如图,抛物线y =mx2-2mx-3m(m ＞0)与x轴交于A,B 两点,与y 轴交于点C,点M 为抛物线的顶点,且OC =OB.

(1)求抛物线的解析式.

(2)若抛物线上有一点P,连接PC 交线段BM 于Q 点,且SΔBPQ=SΔCMQ,求点P 的坐标.

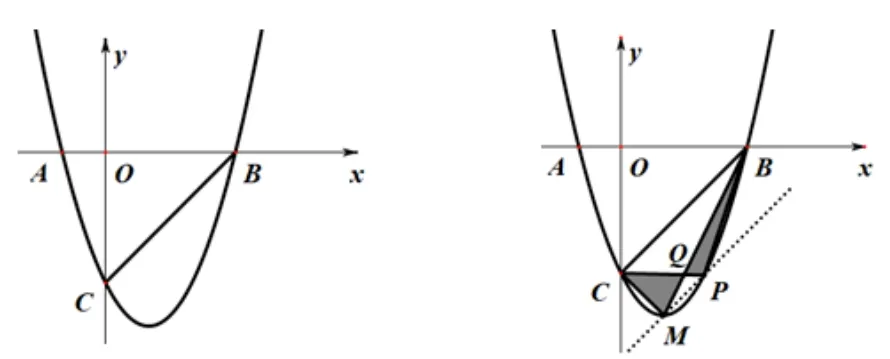
图4

分析本题第一问比较常规, 只需要根据图像与x 轴有两个交点这一信息, 令y = 0 得出等式, 解出A,B 点坐标, 求出解析式中的参数即可.关键的第二问, 给出的条件SΔBPQ=SΔCMQ.利用等量加等量,由SΔBPQ+SΔBCQ=SΔCMQ+SΔBCQ得出SΔBCP= SΔCBM, 两个三角形同底,必然等高,则可推断出M,P 点所在的直线与直线BC 平行,从而求解.

解答(1)令y =0,得:mx2-2mx-3m=0,因为m ＞0同时除以m 得: x2-2x-3=0,解得: x1=-1,x2=3,因为A(-1,0),B(3,0),OB = 3.所以OC = OB = 3,点C在y 轴的负半轴上,所以C(0,-3),所以-3m=-3,m=1,所以抛物线的解析式为: y =x2-2x-3.

(2)根据B 点,C 点的坐标可以求出直线BC 解析式为:y =x-3,因为SΔBPQ=SΔCMQ,所以SΔBPQ+SΔBCQ=SΔCMQ+SΔBCQ,所以SΔPBC=SΔMBC,所以MP//BC,因此直线MP 的解析式可以设为: y = x + n, 根据顶点坐标M(1,-4), 可得直线解析式为: y = x - 5.联立解得:(舍 去), 或

总结平行线间的距离处处相等,将这个相等的距离看作三角形的高,只要在平行线的一条中确定一段线段作为公共的底,那么在另一条平行线中任意确定一点所构成的三角形面积就是一个固定的值.因此便可以产生无数个面积相等的三角形,我们便可以根据这一特性,找到其中符合要求的那一对三角形.

3 借助面积相等的三角形,解决多种常见的几何问题

3.1 解决求定值的问题

例4如图, 点E 在正方形ABCD 的对角线AC 上,且AE = AD, 点P 是BE 上任一点, PN⊥AB 于点N,PM⊥AC 于点M, 若正方形ABCD 的面积是12, 证明PM +PN 是一个定值,并且计算出这个定值．

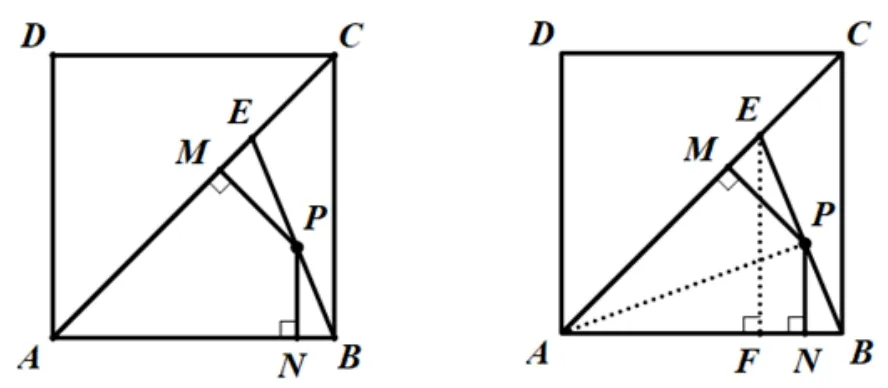
图5

分析连接AP,过E 作EF⊥AB 于F.将ΔABE 分成ΔAEP 与ΔABP 两个三角形.可根据三角形的面积不变的特性,即SΔABE=SΔAEP+SABP,而这三个三角形的底,AE =AD =AB 底相等,那么面积关系就转化为高的关系了.便有PM +PN =EF,求出EF 的长,即可求解.

小结本小题关键在于拆分三角形,将一个三角形分成两个三角形.利用面积不变性,拆分后的两个三角形的面积之和等于未拆分前的一个三角形的面积.再结合三个三角形的底长度相等,得出面积的关系即就是高的关系,从而将两段看似没有联系的线段, 从长度上转化为一条可求的线段,从而得解.等面积法的使用让本题的解答过程变得简单和巧妙.

3.2 分割不规则图形面积的问题

例5如图, 在一块梯形田地上, 分别要种植花生(ΔBEC 部分)和大豆(ΔABE,ΔDEC 部分).若想把种植大豆的两块地改为一块,且使分别种植大豆和花生的面积不变.请问你怎么改种呢?

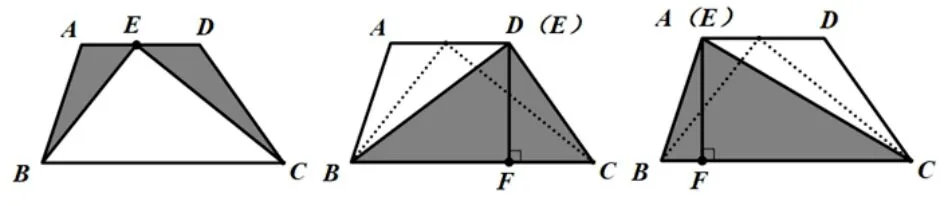
图6

分析本题是一个考查图形变换的题,没有实质性的计算过程.把三个三角形变成两个三角形,并且变化前后的面积不改变.我们只要保证ΔBEC 形状改变而面积不变,那么剩下的ΔABE 与ΔDCE 的面积之和就不会改变.在改变ΔBEC 形状的同时,当剩余的两部能合为一部分时,就解决了问题.

解答因为S梯形ABCD=SΔBEC+(SΔABE+SΔDCE),又因为SΔBEC=EF,当E 在AD 上移动时,EF 的长度始终不变.那么SΔBDC为定值,梯形剩余的面积也不变.所以当E 与A 或D 重合时,连接BE 或CE,所以答案如图所示.

小结解决本题需要弄懂题意,探究图形面积的本质.考虑到三角形的面积跟图形的底和高密切相关,所以我们划分的依据就是保证变化前后的三角形底和高的长度不变化.而梯形提供的一组天然的平行线,就为高的不变性提供有力保障.利用等面积的思想,限定ΔBEC 面积的同时,也可控制剩余部分的面积不变,从而就可以得解.

3.3 解决最值问题

例6抛物线y = -x2+bx+c 经过点A、B、C,已知A(-1,0),C(0,3).

(1)求抛物线的解析式

(2)P 为线段BC 上一点,过点P 作y 轴平行线交抛物线于点D,当ΔDBC 的面积最大时,求点P 的坐标.

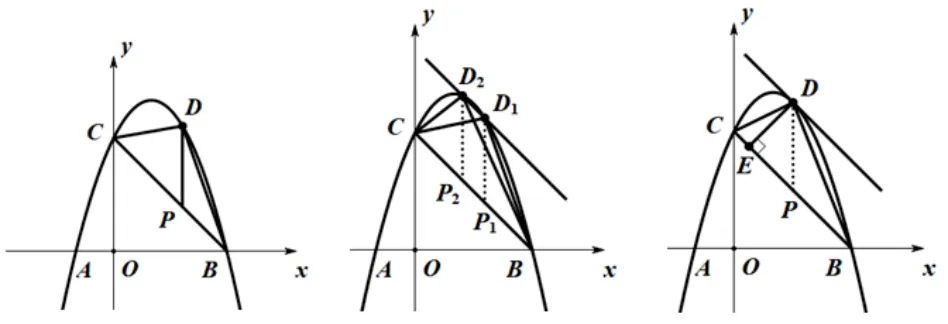
图7

分析本题第一问很常规,利用待定系数法轻松解决.第二问的探究过程需要考虑到面积的最大值.三角形的面积只与底和高相关,当把BC 当底时,变量就只有高了.高的值最大,那么面积就最大.抛物线上的点D 离BC 最远高便最大.因此过D 点平行于BC 的直线与抛物线有且只有一个交点时,这个交点便是离BC 最远的点.求出D 点坐标后,便可得出点P 的横坐标,从而求解.

小结本题是采用将BC 看作三角形的底来求三角形的面积.相比于作铅锤高来求面积规避了大量的化简计算.充分把握住三角形的面积公式的本质,控制一个变量三角形的底BC 不变,去探究另一个变量三角形的高.利用数形结合的思想,让直线与抛物线相切来找到抛物线上与距离最远的点,最远的点就是切点.本题将三角形等面积的特性运用的淋漓尽致.

4 结语

三角形的等面积问题在中学数学阶段往往是渗透化归的思想进行考查的.将求交点个数,求最值,求线段长度等问题转化到三角形求面积的问题中来.这是一个非常实用的解题技巧.它巧妙的避开了大量的运算,提供了简便的方法助我们快速的解答题目.而三角形等面积这一特性的产生就是紧紧围绕三角形的面积公式,在底和高上面进行灵活的变换.等底同高,同底等高,等底等高,实质上是追求底和高在数值上的相等.我们往往需要把握的是通过不同线段之间的运算和转化,保证三角形的底与高变线不变量,就可以保证面积不变.若把三角形面积,三角形的高,三角形的底看作三个变量的话,我们可以知其二求其一.在应用三角形等面积法时,需要明确已知变量和所求变量.掌握三角形等面积法对学生建立等面积思想有极大的推动作用.同时也能够用更加完善学生解几何题的方法和手段.