对2022届佛一模第21题的解法分析及背景探究
2022-10-09江苏省白蒲高级中学226500沈建梅
江苏省白蒲高级中学(226500)沈建梅
在圆锥曲线的问题中,经常考察定点定值问题.面对此类问题时,可先利用特殊点或特殊值验证出定点或定值,再进行求解.求解的方法也主要是利用设而不求,根据题干表示出所有的信息量,再根据之前验证的定点或定值猜想化简的方向.佛山市2022 届高三质量检测第21 题(以下简称22届)便是一道双曲线过定点的问题,笔者对其进行了深入地分析,分别通过代数与几何的视角对该问题进行了分析,并获得了一个一般性的结论.
1 题目及分析
(1)求C 的方程;
(2)点Q(1,0),直线x=t(t ∈R)不经过P 点且与C 相交于A,B 两点,若直线BQ 与C 交于另一点D,求证: 直线AD 过定点.
该模型与2018年全国1 卷第19 题(以下简称18年)以及2015年全国1 卷的第20 题(以下简称15年)的考察形式非常相似,其中18年的试题以椭圆为背景,15年的试题以抛物线为背景.具体题目如下:
(2015年全国1 卷,第20 题)在直角坐标系xOy 中,曲线与直线y = kx+a(a >0)交与M,N 两点.(I)当k =0 时,分别求C 在点M 和N 处的切线方程;(II)y 轴上是否存在点P,使得当k 变动时,总有∠OPM =∠OPN?说明理由.
在上一届即2021 届佛山市高三质量检测中,也出现了一道以该背景命制的试题,题目如下(以下简称21 届):
(佛山市2021 届高三一模第15 题)已知抛物线C :y2=2px(p >0)的焦点为F, 准线l 交x 轴于点K, 过F 作倾斜角为α 的直线与C 交于A,B 两点,若∠AKB = 60°,求sin α 的值.
所以笔者猜想命题老师可能是受到了两道高考题的启发而命制的该问题,对比下来我们可以发现18年的试题是已知两个定点,证明两个夹角相等;15年的试题是已知一个定点以及夹角相等求另一个定点;21 届的试题中的隐藏考点与18年的试题相同是已知两个定点,证明两个夹角相等;22届的试题与15年的试题相同也是已知一个定点以及夹角相等求另一个定点.
在上述几个试题中,分别出现了抛物线、椭圆以及双曲线,我们可以猜想上述模型对任意圆锥曲线都适用.在文[1]中,两位老师对18年的试题进行了详细分析,并总结出如下相关定理:
定理1对于一般的二次曲线:Ax2+Cy2+F =0(AC0).对于该曲线的对称轴上的点P(m,0)(除对称中心外),过点P 的任意直线交该曲线有两个交点M,N, 存在点使得直线QM、QN 的斜率互为相反数.
定理2对于曲线Ax2+Ey+F = 0 的对称轴上的点P(0,m)(除顶点外),过点P 的任意直线交该曲线有两个交点M,N,存在点使得直线QM、QN 的斜率互为相反数[1].
接下来, 本文将对第22 届的试题进行证明与分析.为了体现出一般化, 笔者将原问题推广为如下的一般模型: 已知双曲线= 1(a >0, b >0), 点Q(m,0)(0 <m <a), 直线x = t 与C 相交于A, B 两点, 若直线BQ 与C 交于另一点D, 则直线AD 过定点
2 解法呈现
2.1 基本量法

除了上述证明方法外,我们也可选择构建斜率方程[2],参数方程[1]等等方法进行证明.但为了拓展至一般的圆锥曲线,接下来笔者将利用几何法进行证明.
2.2 利用极点极线进行证明
关于极点极线的说明,极点极线的几何定义[3]: 以椭圆为例, 如图1, P 是不在圆锥曲线上的点, 过点P 引两条割线依次交圆锥曲线于四点E,F,G,H,连接EH,FG 交于N,连接EG,FH 交于M,则直线MN 为点P 对应的极线.
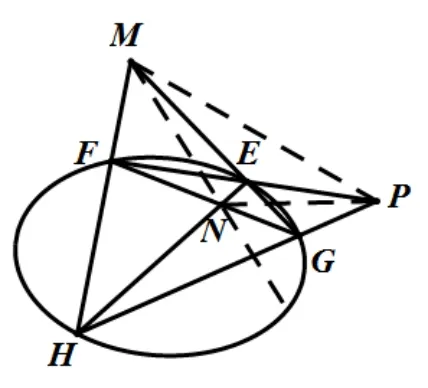
图1
注明所有的圆锥曲线都存在极点极线,读者可自行将该概念延伸至其他圆锥曲线.

注明极点极线的两种定义方式的本质是相同的,对于本文研究的问题而言,利用代数定义进行判断,借助几何定义进行证明.
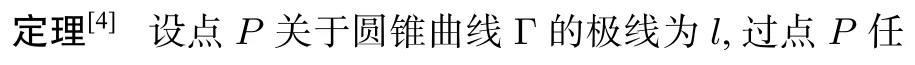


图2-1
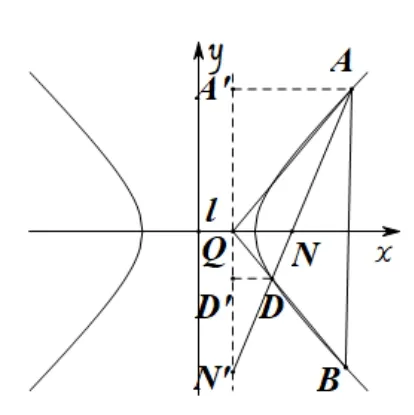
图2-2

