挖掘横向联系 构建研究型课堂——以“椭圆及其标准方程”教学为例

华南师范大学附属中学(510630)周建锋

1 问题的提出

情境认识观认为,知识不是一件事情或一组表征,也不是事实和规则的集合,知识是一种动态的建构与组织.知识是个体与环境交互作用过程中建构的一种交互状态,是一种人类协调一系列行为, 去适应动态变化发展的环境的能力.所以,我们需要构建问题情境,在不断变化的问题情境中去形成这种交互状态,营造研究型课堂的氛围,在探索情境问题的过程中加深对概念的理解,提升数学文化素养.

人教A 版选择性必修一第三章“圆锥曲线”在推导椭圆的标准方程时,一开始用一个平面去截圆锥侧面,先让学生直观感知,当截面转动,会得到不同类型的截口曲线,分别是椭圆、抛物线、双曲线(如图1).接下来推导椭圆标准方程时,突然话锋一转,脱离圆锥截面模型,用平面上到两定点距离和为定值(大于两定点的距离)的点的轨迹模型展示椭圆,从而推导标准方程.

图1

客观来讲,从这个途径引入椭圆,是许多教材采用的方法,浅显易懂,容易建立坐标系,导出方程.但这样一来椭圆的定义和教材对圆锥曲线的引入造成了一个“脱节”,在学生心里必然会留下疑惑: 当截面转动时,截口曲线什么情况下是椭圆,什么情况下是抛物线,什么情况下是双曲线? 对椭圆来讲,这两个模型之间到底有什么联系? 是否还有其它定义的方法? 种种疑问需要我们去解决.

2 教学过程

2.1 研究截口曲线的规律

当截面转动时,截口曲线什么情况下是椭圆,什么情况下是抛物线,什么情况下是双曲线?

设计意图先利用多媒体技术,让学生观察截面变化时截口曲线的规律,形成直观认识.

为此,我们沿截面转动轴的方向作投影,观察一下规律.

设圆锥母线与轴夹角为θ,截面与圆锥轴所成角为φ.

图2

如图2 中第II 种情形,当φ = θ 时,截面与下圆锥一条母线不相交,其余母线(射线)均相交,与上圆锥不相交,侧面截口曲线是一条不封闭曲线;

如图2 中第III 种情形,当0 ≤φ ＜θ 时,截面与上、下圆锥均相交,且上、下圆锥均有无数条母线(射线)与截面不相交,侧面截口曲线是两条不封闭曲线.

这三种曲线我们分别称之为椭圆、抛物线、双曲线,又统称为圆锥曲线.

圆锥曲线与科研、生产及人类生活有着密切的关系,如行星绕太阳绕行的曲线是椭圆、广州塔外形线是双曲线、探照灯轴截面是抛物线等等.我们先来看椭圆相关定义.

2.2 椭圆定义及其与圆锥截口曲线的联系

2.2.1 实验

如图3, 取一条定长的细绳, 把细绳的两端拉开一段距离,分别固定在图板的两点,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?

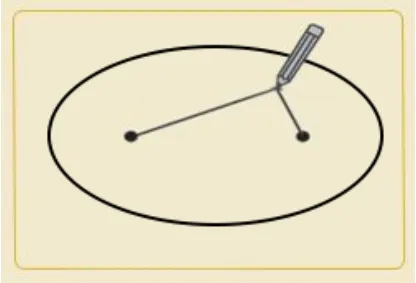
图3

画出的曲线是一条封闭的类似于圆锥封闭截口曲线的图形.

设计意图与教材链接,从平面作图的角度引入椭圆.

2.2.2 椭圆的定义 平面上到两定点F1,F2的距离和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点之间的距离叫做椭圆的焦距,焦距的一半叫做半焦距.

2.2.3 两者的联系

这种方法作出的曲线与截圆锥的第I 种情形类似,都是椭圆,两者之间有什么关联呢?

设计意图将平面作图与课堂开始时的动画规律联系,让学生从中寻找两者的联系.

观察图4,在截面的上、下两部分分别作一个内切球,内切球与截面的切点分别为F1,F2,猜想这两个切点就是我们要寻找的“两个定点”.

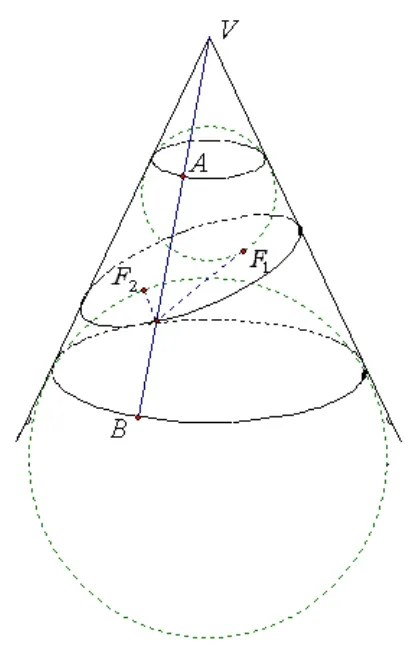
图4

在截口曲线上任取一点P, P 点所在的母线V P 分别与上下两个内切球与圆锥侧面的交线圆交于点A,B,则有PF1= PA,PF2= PB,所以PF1+PF2= PA+PB =AB,而截面固定后,上下两个内切球即固定,AB 为定值.所以图1 中的封闭截口曲线满足椭圆的定义,两者是一致的.

2.3 椭圆的标准方程

观察画出的图形,发现有明显的对称性,如果建立坐标系,如何建系更有利?

以F1F2为x 轴,以F1F2中垂线为y 轴建立平面直角坐标系,设F1(-c,0),F2(c,0),|MF1|+|MF2|=2a(a ＞c).请大家一起完成方程的推导.

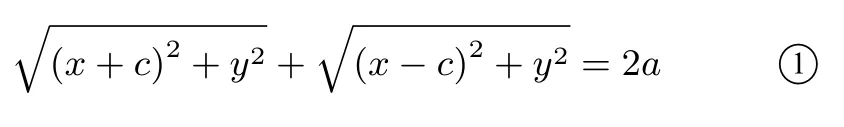
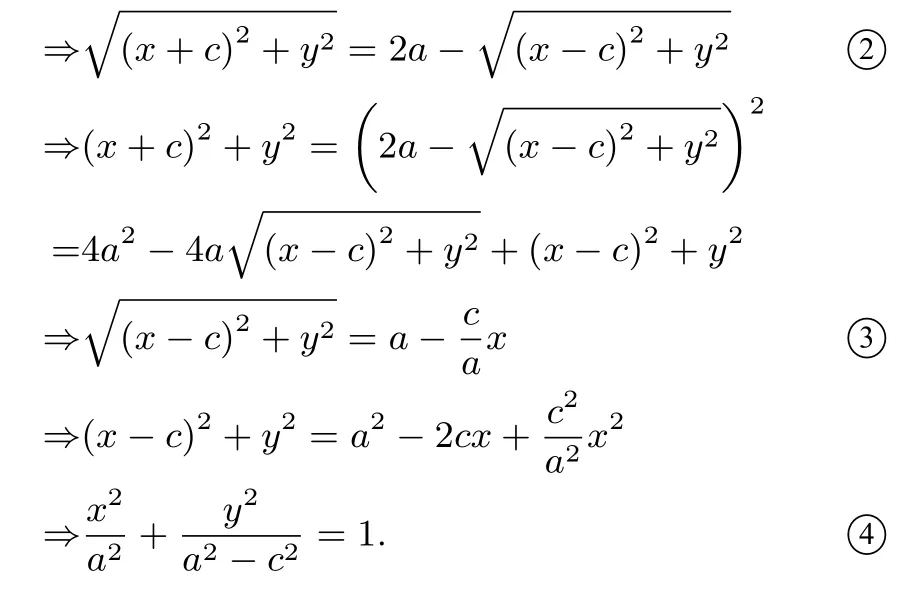
由于a2- c2＞0, 可令b2= a2- c2(b ＞0), 则有=1(a ＞b ＞0).这个方程称为椭圆的标准方程,表示焦点在x 轴上的椭圆.

设计意图引导学生建系,导出椭圆的代数特征,即椭圆的标准方程.

图5

思考1这个标准方程的完备性如何,即每一步变形是否是同解变形?

设计意图强化曲线方程的完备性.

整个变形过程有两步做了平方( ②到③, ③到④),其它移项、同乘(除)非零数均是同解变形.而②③两端均为非负数,所以是同解变形.

思考2a,b,c 在图中的几何意义分别是什么?

设计意图解读椭圆标准方程的参数背景.

分析1c 是半焦距,在图中是焦点到坐标原点的距离;分别令y = 0,x = 0, 分别得到椭圆与坐标轴的四个交点(±a,0),(0,±b),所以a,b 分别是两条对称轴(线段)长度的一半.

分析2如图6, 当点M 运动到y 轴时, |MF1| =|MF2|=a,|OF1|=|OF2|=c,|OM|=b.

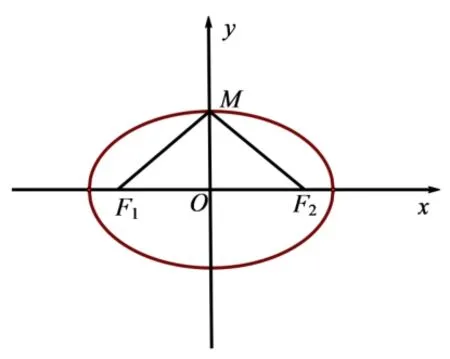
图6

思考3若焦点在y 轴上, 椭圆的标准方程又是什么?(学生自主完成)=1(a ＞b ＞0).

设计意图让学生尝试不同建系下椭圆标准方程的形式.

2.4 再次挖掘新的发现

思考4观察③式,它蕴含了什么几何意义?

设计意图反思标准方程推导过程中隐藏的信息,导出椭圆的第二定义,完成概念的整体设计思路.

这是以后要学习的圆锥曲线第二定义,它将三种圆锥曲线统一起来.

思考5第二定义在图1 的模型中能否体现呢?

设计意图再次与截口曲线模型链接,寻求第二定义与截口曲线模型的内在联系.

分析如图7, 按第二定义, 如何去找出其中的定点和定直线? 截面α 固定后, 与圆锥上部分有一内切球, 内切球与截面α 的切点为F.球与圆锥曲面交线为⊙O,⊙O 所在平面与平面α交于直线l, 猜想点F 与直线l 就是我们要找的定点与定直线.

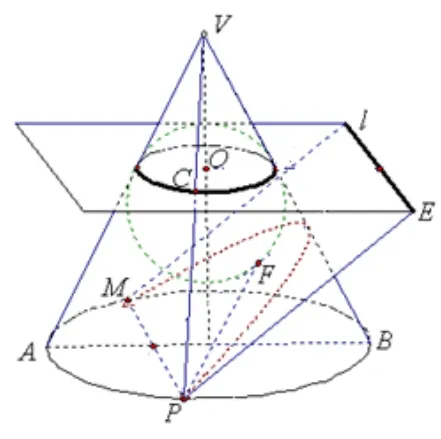
图7

连结V P,交⊙O 于C,则PF = PC(空间一点向球作的两条切线长相等),设点P 到⊙O 所在平面距离为d0,到直线l 的距离为d,则cos θ =而二面角O-l-P的平面角易知为(定值).

由此可见,图1 的模型中既有第一定义的几何背景,也有第二定义的几何背景,它是圆锥曲线统一定义的经典模型.

思考6如何利用圆锥截面模型制定三种圆锥曲线区分标准?

设计意图进一步将第二定义对三种圆锥曲线的分类细化.

2.5 椭圆的其它模型

设计意图利用教材例题,进一步拓展椭圆的生成途径,拓展学生视野.

例1如图8,在圆x2+y2=4 上任取一点P,过P 作x轴的垂线段,垂足为D,PD 中点为M,当P 点在圆周上运动时,点M 的轨迹是什么?

图8

图9

3 教学反思

通过本堂课对椭圆的深入剖析,从圆锥曲线统一定义的角度,充分挖掘其中的关联,让学生大开眼界.

首先,对圆锥侧面截口曲线有较为深入的分析,从直观感知到找出分类标准,对三类圆锥曲线有了更进一步的认识,从中体会到从定性分析到定量分析的一个提升过程.

其次,在传统的模型引入椭圆后,与最初的模型“脱节”,这是一个缺憾,如果不及时弥补,学生的认知会受到阻断.所以,在圆锥截口曲线为椭圆时,如何将它与“两定点”的模型建立联系,寻找两个定点成了关键.此时构造出上下两个内切球,它与截面的切点是两个定点,再利用球外一点向球引的切线长相等,从而证出截口曲线上任一点到这两个定点的距离和为定值,必为椭圆.这样就揭示出了两个模型的内在联系,学生豁然开朗,显得十分兴奋.

第三,推导椭圆标准方程本是一个平淡无奇的过程,但在代数变形过程中,有了一个重大发现,到两定点距离为定值,还可以转化为到一个定点距离与到一条定直线距离之比为常数,直接引出了圆锥曲线第二定义,学生的求知欲再次被点燃.不光于此,一个问题再次被引出: 它与圆锥截口曲线又有什么联系? 又重新回到对圆锥模型的构造,与上次不同,这次是寻找一个定点和一条定直线.定点由前面的经验易得,是上部分的内切球与截面的切点,而定直线又在哪里? 图中除了截面,还要有一个平面才能和截面相交成线.此时内切球与圆锥侧面的切点圆所在的平面“浮出水面”,大胆猜测它与截面的交线就是那条定直线.事实上,经过证明,截口曲线上的任一点到切点的距离与到定直线的距离比确为常数,学生的兴奋点达到了高峰!

最后,利用教材上两道例题,让学生体会到椭圆乃至圆锥曲线,有许多途径可以给出定义,从而进一步拓展学生的视野,激发他们进一步探索的热情.

数学的概念课经常让学生觉得枯燥乏味,是因为没有充分挖掘潜在的元素,没有激发出学生的求知热情.学习数学不仅仅是做题,还要充分理解概念,理解数学,了解每一个概念背景、涵义,以及蕴含在其中的数学思想,把概念讲“活”.深刻理解了概念,学生对数学的理解才会更上一个层次,对提升学生的数学素养有着重要的意义.