局域共振薄膜结构的管腔热声耦合振荡抑制研究

2022-10-09刘杨陈京圳杜敬涛

哈尔滨工程大学学报 2022年9期

刘杨，陈京圳，杜敬涛

(哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨 150001)

燃烧过程中不稳定热释放与燃烧室声场发生耦合后，在接近热声系统共振频率时形成大幅度压力振荡，并会产生强烈的燃烧噪声。特别是对于低排放燃烧系统中的预混燃烧极易引起系统热声振荡，严重影响燃烧系统的安静性以及低排放等性能指标[1-2]。因此，各国学者围绕热声振荡现象的物理机制以及不稳定性控制方面开展了大量研究[3]。Rijke管常被学者用于热声振荡的研究，当两端开口的竖直管路中放入加热丝时，会出现蜂鸣声，即热声振荡现象[4]。基于瑞利准则[5]可知，热源扰动与压力波动同相位时，系统可能发生振荡现象。在热声振荡抑制方面，主要有主动控制和被动控制。主动控制通过增加误差传感器、次级声源以及控制器[6]，对热声系统稳定性进行实时调控。Heckl[7]通过设计次级声源的增益和相位角对Rijke管热声振荡进行了有效调控。Olgac等[8-9]在主动控制系统中引入了时滞积分控制器，可实现系统多模态的不稳定性抑制。主动控制具有较好的实时性和追踪性，但构成较为复杂、成本高，且稳定性影响因素较多，因此，各国学者更青睐于被动控制。被动控制主要通过引入声学结构，如亥姆霍兹共振器(Helmholtz resonators, HR)、1/4波长管、微穿孔板等结构[10-11]。其中，HR共振器受到各国学者的广泛关注。Dowling[12]对亥姆霍兹共振器的数量、颈和腔尺寸进行了详细研究，给出了不同燃烧状态下系统稳定性的调控方案。Olgac等[13]研究了亥姆霍兹共振器对系统稳定性增长率的影响规律，并给出了多个HR共振器的调控方法。Zhang等[14]通过改变HR颈部尺寸设计了可调谐HR共振器。此外，穿孔内衬由于其结构紧凑，声学阻尼性能显著，也被用于热声耦合振荡不稳定性的抑制研究[15-17]。从文献调研可以看出，目前热声振荡控制技术存在控制频率单一，可调性差等局限，难以满足复杂燃烧系统的热声振荡抑制要求。

传统的振动、噪声控制结构在低频宽带以及结构尺寸上常具有一定的局限性。近年来，声子晶体由于具有良好的波操纵能力而受到了大家的广泛关注，这些周期结构中往往存在声学带隙，即声波在相应频带范围内被禁止传播[18-19]。对于依赖周期特性产生的带隙称为布拉格反射带隙，此类带隙受周期结构晶格常数的影响。因此，文献[20]提出了基于共振结构的声学带隙，即局域共振带隙，可实现“小尺寸大波长”的控制效果。

本文提出一种周期分布的局域共振薄膜结构，系统揭示了薄膜结构关键参数对热声系统模态稳定性的影响规律，并探究了声学带隙对模态稳定性的抑制作用。

1 理论模型与公式推导

图1为管腔热声耦合系统-周期局域共振薄膜示意图。其中，管腔两端部声压反射系数分别设为R0和RLd，管长记为Ld。管腔壁面镶嵌周期分布局域共振薄膜结构，薄膜单元长度记为L，第1个薄膜位置坐标记为(x1,x2)，周期距离(晶格常数)为D。在管腔xq处设置一热源，其热释放率记为q′(x,t)=Q′(t)δ(x-xq)，Q′(t)=Qe-iωt，δ为Diracδ-函数。利用线性时滞定律来模拟燃烧热源，有：

(1)

式中：ρ为媒质的密度；c为声速；n为火焰干涉系数；τ为迟滞时间；u-表示火焰上游质点振速。式(1)可在频域内写为[21]：

(2)

可以发现，热源热释放率与热源前端媒质质点振速相关，且存在一定的相位延迟τ，即n-τ火焰模型。此外，一阶火焰模型也常用于燃烧热源的热释放率描述，此类模型求解系统特征根时较为方便，但不能充分表征燃烧系统热、声模态的耦合特性。

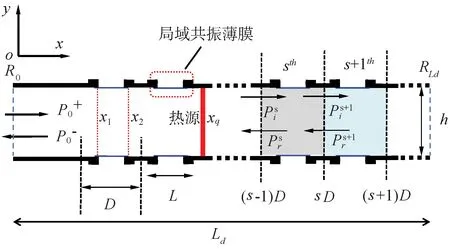
图1 管腔热声耦合系统-周期局域共振薄膜示意Fig.1 Schematic diagram of the tube thermoacoustic coupling system with periodic locally resonant membranes

在热源附近应用声压以及质量连续性条件，可得：

Axqe-ikxq+Bxqeikxq=Cxqe-ikxq+Dxqeikxq

(3)

(4)

式中k为波数，k=ω/c，对于两端紧固的薄膜结构，其位移表达式可以写为：

(5)

式中：A为位移函数的系数向量；Ψ为振型向量。通过能量原理可以求解管腔-薄膜耦合系统动力学特性[22]，即：

Α=(K-ω2M+iωG)-1Pi&r=ΠPi&r

(6)

式中：K和M是膜的刚度和质量矩阵；G是管腔中膜辐射声的贡献矩阵；Pi&r表示薄膜上方声压作用项。

肿瘤组织间碘-125放射性粒子植入术作为临床肿瘤治疗方式之一,可应用于多种肿瘤的治疗中,治疗效果较好。但是手术过后需要对患者开展严密的护理,才可保证手术效果,提升预后。

Pi&r=AsP1+Bs+1P2

(7)

(8)

根据第s个薄膜两端声压连续性条件，有:

(9)

(10)

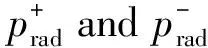
(11)

(12)

管腔进出口边界条件可通过反射系数R0和RL分别表示为：

A0e-ik0=R0B0eik0

(13)

ALde-ikLd=RLdBLdeikLd

(14)

联立式(3)、(4)、(9)、(10)、(13)和(14)，可以得到一系列线性方程组，整理为矩阵形式：

(15)

式中：Γs表示第s个薄膜两端声压传递矩阵；Θ则表示火焰两端声压传递矩阵，分别表示为：

(16)

(17)

观察式(15)～(17)可以发现，系统角频率ω为未知量。因此，可令式(15)中系数行列式为零求解出系统特征根ω。由于热源的干涉作用，系统特征根将是复角频率，其实部表示系统的固有角频率，与系统振动特性有关，虚部则称为稳定性增长率，即ω=ωr+iωi。当所求特征根虚部大于零，则系统在该激振频率下将处于不稳定状态，即系统响应发散。当所求特征根虚部小于零时，系统将处于稳定状态。

2 结果分析

对于具有燃烧热源的管腔结构，如图1所示，由于热源不稳定热释放的存在，系统的模态固有特征可能会产生不稳定性，即当固有角频率虚部(增长率)大于零，模态不稳定。本文首先验证模型的准确性，选用文献[21]中的物理参数如表1中所示。

表1 系统模型参数Table1 Model parameters of the system

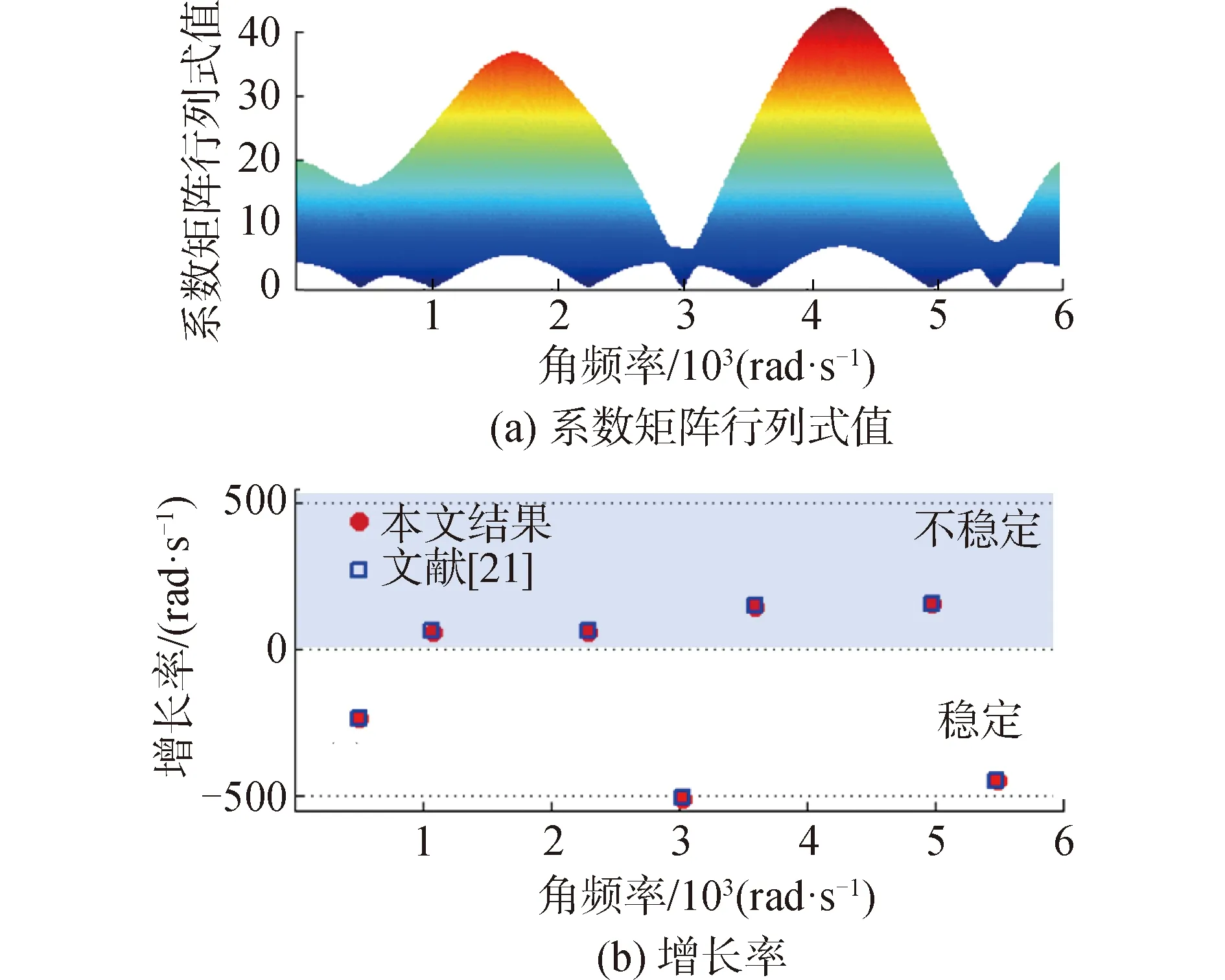
图2 管腔热声耦合系统模态特征Fig.2 Modal characteristics of the tube thermoacoustic coupling system

接下来，在管腔热声耦合系统中引入局域共振薄膜结构，管腔参数保持不变，薄膜镶嵌位置(0.5 m, 0.6 m)，长度分别取L=0.05、0.07和0.1 m，以薄膜长度L=0.1 m为参考选取薄膜无量纲张力F*=F/ρc2L=0.1，无量纲质量密度m*=ρm/ρL=1，F为薄膜张力，ρm为质量密度。系统特征根分布情况如图3所示。图中方框表示未加薄膜时系统特征根，很明显薄膜结构对系统模态不稳定性有明显的抑制效果。当薄膜长度L=0.1 m时，系统大部分模态均为稳定，充分证明了局域共振薄膜结构的多模态控制效果。图4给出了连续变化的薄膜长度对系统热、声模态固有频率的影响，显然，薄膜结构对某些声模态固有频率产生较大影响，而对热模态频率影响较小。这是由于热模态与热源自身特性有关，即使管腔不存在驻波模态，热源自身所形成的局部反馈回路，也会引起系统的不稳定性。而热模态振型分布与其周围声模态有关，因此可以通过改变声模态特性，进而实现热模态稳定性的间接控制。

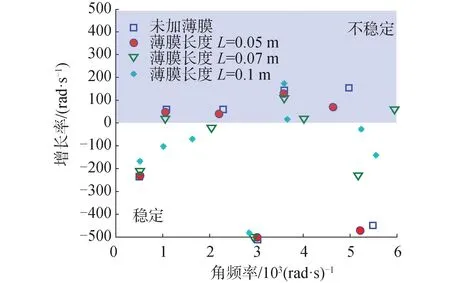
图3 不同长度的薄膜对系统模态特征的影响Fig.3 Effects of different membrane lengths on the modal characteristics of the system

图4 不同长度共振薄膜对系统固有频率的影响Fig.4 Influence of different membrane lengths on the natural frequencies of the system

薄膜张力对系统前5阶模态稳定性的影响绘制在图5中，图中的“+”“-”号对应增长率的稳定性，负为稳定，正为不稳定。可以发现，薄膜无量纲张力F*在0.05～0.2，可使系统前4阶模态同时稳定，然而对第5阶模态不稳定性控制效果较小。当薄膜张力趋于无穷大时，薄膜结构相当于刚性壁面，因此不会对系统模态稳定性产生影响。以上研究充分说明局域共振薄膜结构的多模态稳定性调控能力。

图5 不同薄膜张力对系统模态特征的影响Fig.5 Effects of different membrane tensions on the modal characteristics of the system

接下来探究周期分布的局域共振薄膜对系统模态稳定性的影响。管腔参数不变，第1个薄膜位置为(0.2 m，0.3 m)，周期分布距离D=0.11 m，共振单元数量Scell=5。分别计算管腔热声耦合系统未加薄膜和加周期薄膜后的系数矩阵行列式值，并绘制在图6中，行列式值趋于零时的频率表示系统的特征根。显然，由于周期薄膜结构的引入，导致热声耦合系统在2 920～5 460 rad/s内不存在特征根，而此范围正是周期结构在管腔中产生的声学带隙。可以发现，系统特征根的分布形式发生了重组，即一些模态受到带隙的影响后会急剧向低频偏移。图7给出了系统模态频率和增长率的变化情况，当引入周期薄膜时，系统的四阶不稳定模态增长率均减小，充分说明了周期结构对热声耦合系统不稳定性的有效改善作用。

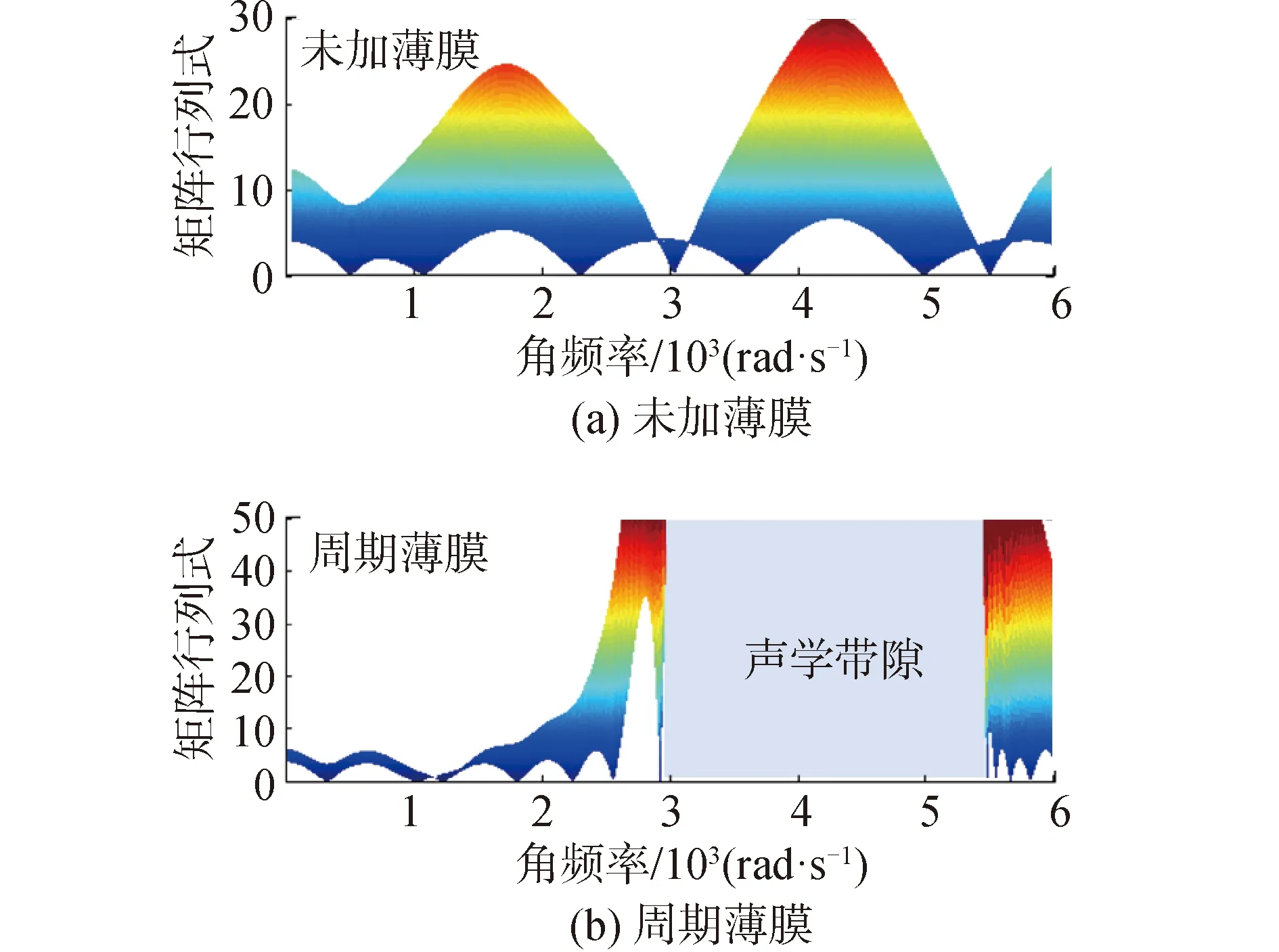
图6 周期分布薄膜结构对系统特征根分布的影响Fig.6 Influence of the periodic membranes on the characteristic root distribution of the system

图7 周期分布薄膜结构对系统模态稳定性的影响Fig.7 Influence of the periodic membranes on the modal stabilities of the system

对于本文提出的局域共振周期结构，一般存在2种带隙，即局域共振带隙(Locally resonant bandgaps：RBG)和布拉格反射带隙(Bragg reflection bandgaps: BBG),RBG受薄膜共振频率影响，BBG则受周期距离影响，图6中的带隙属于BBG和RBG的耦合情况。当改变薄膜张力时，可以调节RBG的位置，如图8(a)所示，减小无量纲张力F*=0.05，系统的局域共振带隙向低频偏移(1 830～3 970 rad/s)。此时RBG和BBG解耦，4 320～5 240 rad/s则是布拉格反射带隙。当增加薄膜张力时F*=0.15，如图8(b)所示，RBG向高频移动，但仍与BBG耦合，因此带隙整体向高频移动。在带隙范围内，系统不存在特征根，因此可人为调节RBG位置，进而在特定频段范围内保证系统的绝对稳定性。