“研趣”学习：实现学生数学思维进阶的应然追寻——以“三角形‘变形计’”一课为例

江苏省南京市百家湖小学 王 军 黄德忠

有关三角形的面积练习中有这样一道题目（见图1）引起了笔者的注意。这道练习题的设计意图是让学生通过在平行线之间画出两个与指定三角形面积相等但形状不同的三角形来感受三角形的等积变形。对于这道练习题的教学处理，教师往往止步于“等底等高”的三角形面积相等的结论，使学生的数学思维和空间观念的发展比较有限。因此，笔者从图形运动变化的视角出发，对这道练习素材进行了更为深入的发掘和处理，与学生开展了以“三角形‘变形计’”为研究主题的探究活动课，以期激发学生数学学习的研究乐趣和达成深度学习目标。

图1

一、教学过程

师（出示课题：三角形“变形计”）：同学们，今天我们要学习的内容与三角形有关，你们会算它的面积吗？

生1：底×高÷2。

师：回到课题，猜一猜，我们今天会变三角形的什么呢？

生：可能会变三角形的形状、底、高、面积或者周长。

师：有这么多的可能，看来今天这节课会有点意思。那咱们就一同走进“变形”的世界吧。

师：看，同学们能利用掌握的知识求出涂色部分的面积吗？（见图2）

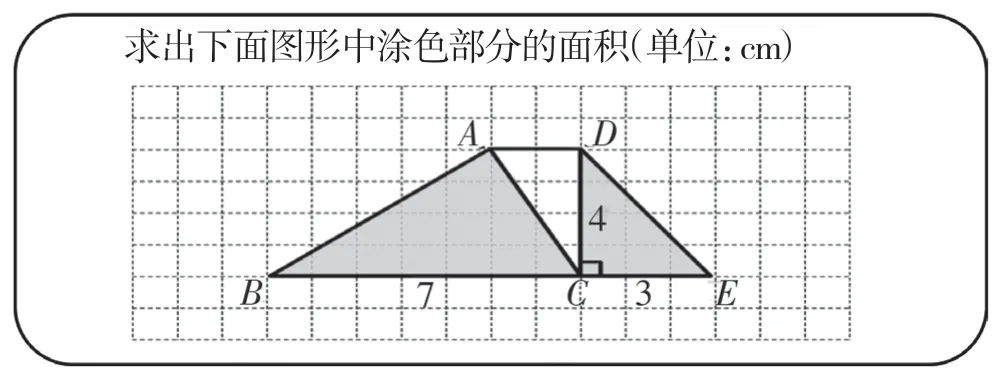
图2

师：同学们解决了吗？谁来分享一下你的解答过程？

生2：先算直角三角形DCE的面积是3×4÷2=6（平方厘米），再算三角形ABC的面积是7×4÷2=14（平方厘米），最后算出面积和是6+14=20（平方厘米）。

师：你怎么知道三角形ABC中BC边上的高是4厘米？

生3：因为AD与BE是相互平行的，DC是三角形DCE中CE边上的高，垂直于CE，因此，DC的长度就是三角形ABC的高的长度。

师：原来是利用了平行线之间的距离处处相等的特征。其实，在这里，这个距离就是三角形ABC和三角形DCE底边上的高。

师： 能利用学过的知识解决问题，真聪明。同学们还有不一样的方法吗？

生4：我是这样解决的，连接AE，那么大三角形ABE的面积就是原来两个小三角形的面积和，因此，面积和就是（7＋3）×4÷2=20（平方厘米）。

师：方法很奇特！谁能理解他的解题方法？

生5：他的方法其实就是将三角形DEC的D点向左平移运动到A点，将三角形DCE变成三角形ACE，然后和三角形ABC合并成大三角形ABE。

师：你们俩的方法是这个意思吗？请大家观察在D点移到A点的过程中，三角形DCE变成三角形ACE后，什么变了？什么没变？

生6：底没变，都是以CE为底，高的长度也没变。

生7：三角形DCE变成三角形ACE后形状变了，但是面积没变。

师：那你们现在能解释为什么三角形ABE和阴影部分的面积和相等？

生8：三角形DCE与三角形ACE同底等高，所以面积相等。因此三角形ABE可以看成两个小三角形的面积和，与阴影部分的面积和相等。

师：有意思，一个点的移动就给我们解决问题带来了这么大的方便。那这里会移动的点还藏着什么奥秘呢？下面，我们一起来研究下面的探究活动（见图3）。

图3

（学生自主画图操作，教师巡视并指导。3分钟后，全班交流）

师：这几名同学画的三角形都符合要求吗？

生9：它们的底相同，都是BC边；高的长度相等，都是4厘米。所以面积都相等。

师：像这样以BC为底，高相等的三角形还有吗？

生10：有，还可以画出很多。请大家看我画的作品。（见图4）

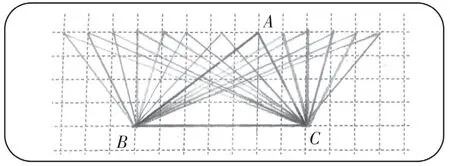
图4

师：画出了这么多的三角形？观察一下，什么变了？什么没变？

生11：三角形的形状变了，面积没变；高的位置变了，底的位置没变。

师：真棒，你的数学眼光真敏锐。请同学们仔细观察这几名同学的作品，说说有什么发现。

生12：我发现其实就是三角形的顶点A在移动，而底边BC保持不变。

师：有意思，只是一个顶点A在移动。那A点除了我们画出来的这些位置，还能移动到哪儿呢？

生13：我发现符合要求的点都在过A点且与BC边平行的一条直线上移动。

师：为什么在这条直线上移动就能保证面积相等呢？

生14：首先底边BC不变，底是相同的，而顶点在这条平行线上移动，高的长度也会保持不变。同底等高的三角形面积相等。

师：原来这里还是利用了平行线之间的距离处处相等。

师：只能移动A点画面积相等的三角形吗？观察思考一下，还可以怎样？试着把你的想法在图上画出来。

学生代表的作品依次呈现：（见图5）

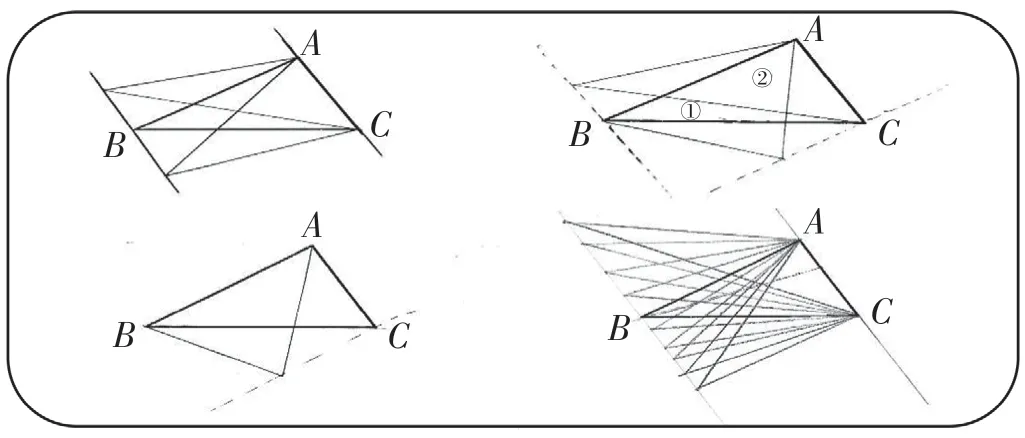
图5

师：谁来说一说只要怎样画就可以？

生15：过B点或C点作对边的平行线，在平行线上任意取一点，都可以画出面积相等的三角形。

师：原来我们可以像这样任意移动三角形的一个顶点，都能画出无数个面积相等的三角形。

师：通过刚才的探究活动，相信同学们对三角形的“变形”有了一定的认识。带着我们的发现，回到一开始的问题，你们现在能解释那名同学解决问题的奇特方法了吗？谁再来解释一下。

（学生尝试解释。教师呈现移点合并的动画过程）

师：除了将D点移动到A点，还可以怎么移动？

生16：可以将A点移动到D点，也可以将A点和D点同时向中间移动。

师：在刚才的学习过程中，你们有什么发现？

生17：都是在平行线上移动顶点把两个三角形合成一个底为10厘米、高为4厘米的三角形。

师：那这里合并后三角形的顶点其实就是原来的A点？D点？AD点？其实也可以是新的名字——F点。

师：俗话说：“合久必分，分久必合。”刚刚研究了“合”，我们再来看看“分”的情况。

师：看，这就是我们一开始遇见分成两个三角形的情况。（动画演示）（见图6）

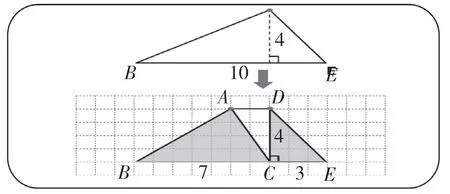
图6

师：通过刚才的研究，我们知道上下两个图形的面积是一样的。

师：请大家想象一下在大三角形的这个顶点里真的只能包含两个点，分成两个三角形吗？

生18：还可以分成三个三角形，四个三角形，无数个三角形。

师：那我们一起来看一看分成三个三角形的情况。（动画演示）（见图7）

图7

师：谁能把这三个点还原回去验证一下面积变了没有？

（引导学生利用同底等高、移动顶点合并三角形的方式还原成一个三角形）

师：还可以怎么分？请同学们自己画一画。

师：谁来说一说怎么验证面积不变？

（学生小组交流，尝试运用动点合并的方式验证面积不变）

师（小结）：无论分成多少个三角形，面积总是不变的。

师：同学们，一个原本图形中静止不动的点就这样被我们给玩“活”了。它里面竟然包含着这么多的数学智慧。我们还可以怎么研究三角形的“变形”？

生19：还可以研究三角形的底。

师：除了研究三角形之外，还能研究什么图形？

生20：还能研究长方形、平行四边形、梯形、多边形。

师：是的，我们还可以研究很多图形。更多的奥秘就留给你们课后自己去探索吧。

二、教学反思

（一）设计“研趣”活动，优化深度学习的思维历程

发展学生的空间观念需要教师有效利用探究素材和组织活动激发学生的学习动机，并让学生充分经历观察、比较和思考的研究过程，通过动态变换和空间想象的手法促使学生对图形的认识从静态固化逐步过渡到动态变化，从而让学生把握图形与几何知识学习的本质。在教学中，笔者将常态下的三角形面积问题进行了有机改造和适度延伸，引导学生经历了 “动点巧解面积问题—寻找等积变形的动点轨迹—三角形的分解与合并”的趣味学习活动，使学生深入体会用运动变化的观点认识和思考三角形及其变化方式、图形与图形之间的关系等。同时，笔者有意识地将学生画出的变式三角形进行有序整合，促使学生借助观察这种运动变化中的“瞬间图形”思考和联想其中更多的变化和规律。因此，这样充满研究乐趣的学习历程不仅有利于激发学生的学习动机，打破学生意识中原有的静止、绝对的空间观念，还有利于在潜移默化中帮助学生自然而然地建立起动态、变化的空间观念，真正实现数学深度学习。

（二）创生“研趣”氛围，导引思维可视的学习进阶

教师在运用动态手法进行教学的过程中，应适时地给学生提供应用知识的机会，尤其是让学生进行数学思维的可视化表达，将自己内隐的、潜在的思维过程通过外显、直观的创生活动表达出来。这不仅有利于课堂生成更多有价值的资源及展现学生获取知识的思维过程，还有利于激发学生积极主动地完善对知识的理解，形成动态化的分析思路。在教学中，笔者精心安排了让学生自主画图操作的创生活动。学生一个个充分发挥想象力和创造力，巧手设计三角形的变形分解与合并。在充满研究乐趣的创生活动中，学生不但设计出大三角形分解成四个、五个、六个小三角形的变形情况，还想象推断出其能分解成无限个小三角形，并且能灵活运用点的运动来进行逆向的还原合并。所以，这种直观物化与动态想象相结合的创生活动，不仅促进了学生运用运动变化的观点进行学习探索，还使学生在分析、思考和理解三角形变形分解与合并的同时，感受到了事物之间存在的“静止到运动、绝对到相对、有限到无限、量变到质变”的辩证思想，实现了数学学习的进阶。因此，动态思路的建立不仅有助于学生更加灵活地分析和处理图形与几何领域中的有关问题，还将推动学生的思维发展。

（三）凸显“研趣”价值，聚焦问题解决的思维本质

在教学中，学生的注意力和思维力不能仅仅停留在图形表面的变化上。教师应引导学生从联系的视角出发，在图形运动变化的过程中，观察、分析和思考其中的不变因素，归纳总结其本质规律，形成结构化的知识图谱。这样，学生便能摆脱细节的羁绊，从全局上分析问题的本质，形成从整体上把握的一种数学思维方式。在教学中，笔者让学生在画出同底等高的三角形后，聚焦观察这些三角形的联系，从而得出等积变形的动点轨迹及面积相等的特点，并将这个规律推广至“另外两个顶点”。此外，笔者还引导学生通过想象推理、动手操作、还原验证等方式，探索三角形分解变形及合并过程中整体和部分各个量之间的变与不变，深入体会图形之间的联系。其实质便是让学生把握“同底等高”三角形面积相等的本质，从整体出发进行研究和思考。值得注意的是，这种结构化的整体思想还具有一定的应用价值。学生在学习“圆的面积公式”推导时，将圆分成若干个近似三角形的小扇形后，就可以从整体出发，通过等积变形将它们转化为与之面积和相等的大三角形，进而推导出圆的面积公式。因此，我们可以预见，这样结构化的整体思想必然会促使学生在探索学习中不断发现新的方法、新的联系，拓宽解决问题的思路，形成独特的数学眼光。