基于“活教育”思想观照,提升学生的高阶思维能力
——以“钉子板上的多边形”教学实践为例
2022-10-08江苏省南京市江宁区岔路学校
江苏省南京市江宁区岔路学校 胡 静
学校“活课堂”教改的理论依据来源于我国著名教育家陈鹤琴的“活教育”思想。陈鹤琴先生的教育主张:从儿童立场出发,发现和引领儿童;凡是儿童自己能够做的,应当让他自己做,在做中学;凡是儿童自己能够思考的,应当让他自己思考,在思中进。陈鹤琴先生的主张对“双减”背景下的课堂教学仍有很大的指导意义。
“双减”背景下,落实“学科核心素养”,应关注并努力思考和激活课堂教学要素,即问题情境、合作探究、倾听与对话、交流与展示。催生指向“核心素养”的教与学,已根植、深入每位教师的内心并落实于行动,以此形成包括教师与学生、个体与小组、小组与小组间不同层次的互动。课堂上的教学互动,不仅要关注学生参与课堂交往的主动性,而且要把握学生的思维是否被激活,能否深化学生的数学思考,提升其高阶思维能力,从而使课堂成为学生的成长之地。教师和学生组成活生生的学习型组织,学校成为应用之场、思辨之所、创新之地。
如何提升学生的高阶思维能力?下面笔者就苏教版数学五年级上册的一节综合实践课“钉子板上的多边形”谈几点实践思考。
思考之一:自主建构的历程需不需要错误磨砺——捕捉与摒弃
叶澜教授说过,课堂应该是向未知方向不断挺进的探究旅程,随时都有可能出现意外的通道和美丽的风景,而不是一切都必须遵循固定路线而没有激情的行程。儿童的学习是儿童本身的认知框架不断变革和重组建构的历程。课堂有时会出现许多“意想不到”的生成性资源,有时是正确的,有时是错误的,作为教师,我们不能拘泥于先前的预设,回避或视而不见错误,必须捕捉有价值的“意外”资源,摒弃不合理的错误资源,巧妙地引导学生“数学地思考”,通过自省,更新重组认知结构,必然能达到提升思维能力的目的。
【片段一】自主探索内部只有1枚钉子的多边形面积规律
(1)活动:下面的多边形面积各是多少平方厘米?每个多边形边上的钉子数各有多少枚?数一数、算一算,将结果填入表中。
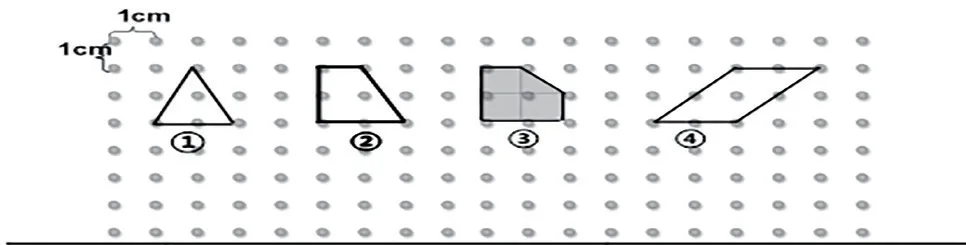
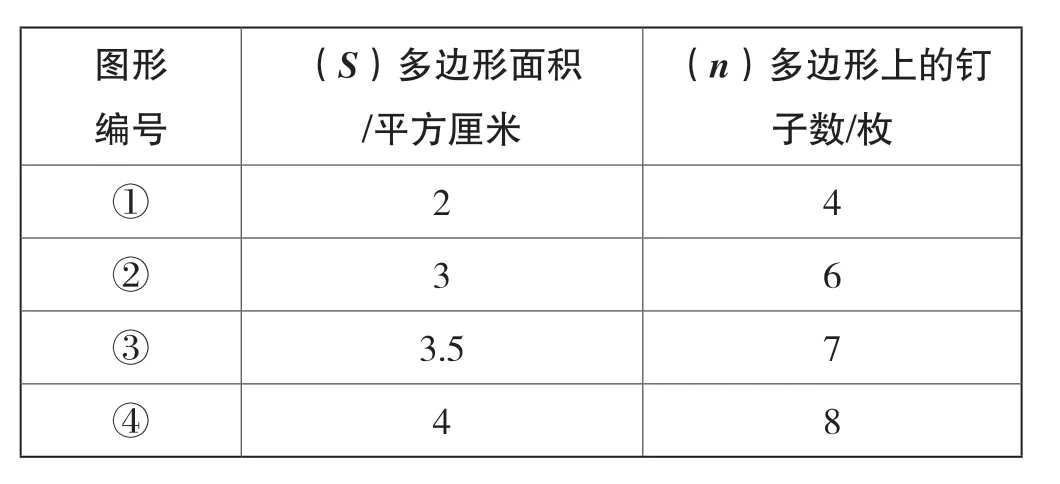
?
(2)发现规律:多边形的面积=多边形边上的钉子数÷2。
(3)举例验证。
师:这个发现对不对呢?怎么验证?
生:我们可以再举几个这样的例子验证一下!(学生验证交流)
师:老师看到有些同学眉头紧锁,你们遇到了什么问题?能和大家分享一下吗?
生1:老师,我的验证符合刚才的规律。
生2:老师,我的不符合。
生3:老师,我的也不符合,但是我验证的方法是对的。
师:哦?我们一起来看看!
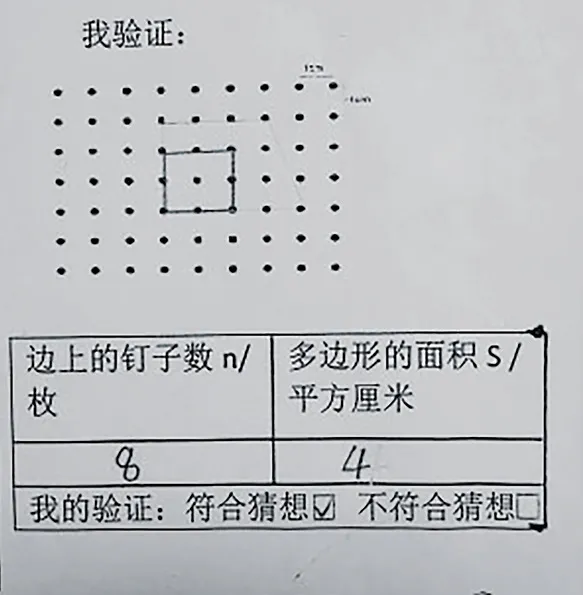
图1
师:看来,图2和图3确实不符合我们的规律!那为什么这个规律有时管用,有时却用不了呢?别着急,请仔细观察这些图形,同桌之间讨论你们的想法。
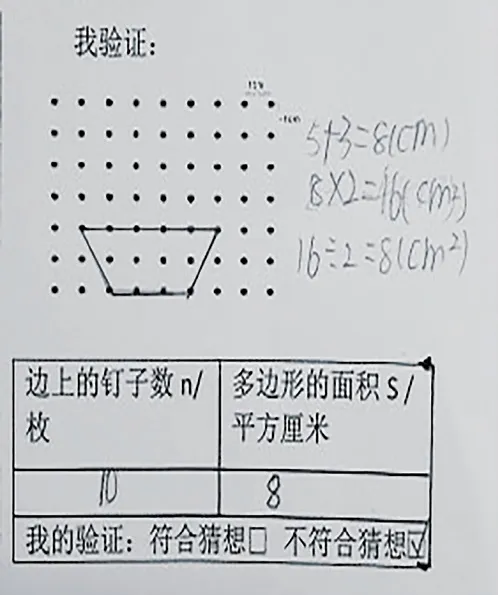
图2

图3
生1:我发现这些图形的高都是2。
师:好,老师把你的发现记录下来,是这样的吗?
生2:我不同意你的看法,我画的图形高是3cm,同样符合规律。
生3:是的,我画的图形高是5cm,同样也符合规律。
生4:我们小组发现,符合规律的都是内部钉子数是1的情况。
师:是这样的吗?
师:你们小组能从不同的图形中发现共同点,真是善于观察!也就是说,S=n÷2在什么情况下才成立呢?如果用a表示内部钉子数,即a=1时,S=n÷2。
师(小结):看来不仅要善于发现规律,而且要主动去验证规律,这样才能得出正确的结论。
【解读】本环节主要引导学生明白规律要具有普遍性。首先,由简单的多边形入手,初探规律。其次,延伸到用任意多边形来验证结论,发现结论不能适用于围成的每一个多边形。这就引发了学生的思考:“是刚才的结论错了吗?若没有错,为什么有些多边形没有这样的规律呢?”产生了这样的困惑,学生就会主动地去探究症结所在,在这样有目的的探究中终于明白结论不具有普遍性。最后,通过小组内的合作完善结论,在验证成功、持续应用中形成第二次认知冲突,引发学生探究。学生发现钉子板上多边形的面积不仅跟边上的钉子数有关,还跟多边形内部的钉子数有关,在产生猜想和验证不成立的冲突后,学生提出:“这些图形的高都是2cm。”教师对此并没有采取否定和回避态度,而是让学生通过自我辩论形成有价值的思考,从而实现认知结构的更新。
思考之二:怎样验证猜想——让“数学模型”助力“符号意识”
“钉子板上的多边形”是一节探究规律的实践活动课,在学生通过数据整理初步提出猜想后,怎样让学生验证猜想才能实现深度学习呢?
【片段二】探究内部钉子数
师:接下来,我们要研究内部钉子数a=3,a=4时的情况,谁能猜猜S等于什么?
生1:当a=3时,S=n÷2+2。
生2:当a=4时,S=n÷2+3。
师:这个猜想正确吗?我们还需要进行——(生齐答“验证”)
师:请大家选择一个感兴趣的多边形进行研究,验证面积与边上钉子数是否有这样的关系。
(学生验证,汇报交流)
师:我们接着往下写,写得完吗?谁能概括一下这个规律?
生3:S=n÷2+(a-1)。
师:那我们往上想,如果a=0,S 等于多少呢?你是怎么想到的?
生4:当a等于0时,S=n÷2-1。
师:到底对不对呢?我们来验证一下。谁来指一指,这减少的1在哪里?
师:这个多边形,内部钉子数是0,面积怎么算?
生5:S=6÷2+0。
师:老师把中间这个钉子上移1格,现在这个多边形内部钉子数变成了多少?
生6:0。
师:面积怎么算?S=6÷2-1,减去的1在哪里?你能在图中指一指吗?(再次证明了这个规律)
师:我们再次回到黑板上,观察我们得到的这些结论,你有什么发现?
师:当多边形内部钉子数为a时,S=n÷2+(a-1)。
师:接下来,大家觉得我们会研究什么问题?研究的时候有什么好的建议?
1.基于学生学习的选择
一节优质的数学课,不应该在各种“创新”的外表形式上卖力,而应变革教学方式方法,本真地对待学生。开展的教学活动应该有学生本位的思想,从学生的立场出发,引领学生。
(1)自己“做”研究材料。由教材例题提供研究材料转为现场“做出”研究材料。首先组织学生研究多边形内有1、2枚钉子的情况,研究的学习素材是教材提供的典型多边形的材料,在验证环节和研究多边形内部有3、4枚钉子的多边形面积时,所有的研究材料都是学生自己现场画出来的。
(2)自己选择探究方向。 每个环节结束,教师都会问:接下来我们将会研究什么?学生都能按照预设自己选择下一个探究方向。
(3)自己选择策略方法。 “从最简单的内部钉子数是1研究起”“要验证”“咱们多画几个多边形举例,固定内部钉子数,数出边上的钉子数……”学生自己选择研究策略,根据自己设计的研究方案,自主在钉子板上围出几个多边形,计算并记录数据。教师则相机引导学生把这些具有相同关系的多边形进行对比,发现它们的共同点,继而发现多边形的面积与它边上钉子数的关系。
自己选择探究方向,自己选择策略方法,自己“做”研究材料,这样的探究活动更加原生态,能让学生获得探究过程的“真”体验。由这样的体验中总结出来的活动经验,更容易迁移到新的探索活动中。
2.触及数学知识本质的“大问题”
“当多边形内有1枚钉子时,它的面积和边上的钉子数有什么样的关系?”“图形内有2枚钉子时,图形面积和边上的钉子数有怎样的关系?”“图形内有 3 枚、4 枚……钉子时,图形面积和边上钉子数分别有怎样的关系?”“你能用一个含有字母的式子概括出以上所有的规律吗?”这一连串的提问能够引发学生思考,直到触及数学知识本质的“大问题”,从而将学生思维引向深入,引导学生由浅入深、由表及里地剖析问题本质。
3.数学模型助力符号意识
数学学科是强调“建模”的学科:建立模型—解释模型—应用模型。其实,这就是一个符号化的过程。因此,数学模型的建立与学生符号意识的培养密不可分。
本节课教师从内部钉子数为1开始探究规律,引导学生运用不完全归纳法发现了格子中多边形的面积与相关格子点数之间的关系,应该说这一过程侧重培养了学生的合情推理能力。学生通过寻找不同式子的共同特点,类比推理得到了更具一般意义的 “通用公式”,这一过程侧重锻炼了学生初步的建模能力。归纳推理与演绎推理交相呼应、相映生辉,学生的推理能力和初步的建模能力在充分思辨的过程中得到了实质性的提升。
思考之三:永续的“学力”:从“知识本位”走向“方法习得”——自我性监控
对于探索规律的教学,教师除了要关注“探究什么”,更应关注“用什么探究”和 “如何探究”,不仅要让学生习得规律性的知识,还要教给他们“能够带得走”的永续的学力。
自我性监控是一种高层次的思维活动,是指学生自主设计探究方案、自我实施方案以及回顾反思整个学习历程,以加深对知识的理解,促进思维品质的提升。本节课在探究S=n÷2规律后,设计了及时组织学生进行回顾探究过程、掌握自主操作探究的方法这样一个环节:确定内部钉子数、画出多边形—算出多边形的面积—观察类比、提出猜想—举例验证—得出结论—用含字母的式子表示规律。通过对学习过程或某一环节的回顾、整理,展开思辨性、批判性思维,这就是自我性监控的思维。它是一种反思性思维,有利于学生数学活动经验的积累。学生有了这些数学活动经验的指引,内部钉子数是2、3、4……的多边形面积与边上钉子数和内部钉子数存在的规律就水到渠成地被探究出来。这种经验的改造和重组、超越与提升,使探究学习不断向纵深处推进,不仅让学生掌握了科学的探究方法,而且发展了学生的高阶思维能力,从而为后续学习提供不竭的动力。
本节课的探究活动并不以得到皮克定理而终止,“为什么要再减去1?”“经历了探索的过程,对于皮克定理你还有什么想进一步了解的吗?”这些问题将学生带入深层次的思考:立体图形也有皮克定理吗?进而引发学生新一轮的思考和探索。
