应用学习科学 巧构线上课堂——以北师大版数学五年级下册《倒数》教学为例

广东省深圳市福田区东海实验小学 谭春兰

2020年春，突如其来的新冠肺炎疫情，让春季学期开学延期，随着教育部《关于深入做好中小学“停课不停学”工作的通知》的印发，线上教学走入大众视野。2022年，新冠肺炎疫情再次来袭，部分地区的教师不得不再次面对线上教学。但经过两年的沉淀，这一次，教师不再慌于应对，而是更为沉着冷静地思考、研究如何让线上教学更加高质高效。笔者所在的深圳市福田区，自线上教学以来，每周开展一次面向全区的线上教学展示课，最高在线观摩人数超过7000人，由此可见，一线教师对如何更好地设计与实施线上教学有着强烈的需求。

作为一线教师，笔者对线上教学有着较为丰富的经验；作为本校线上教学巡课小组成员，笔者有大量机会观摩线上教学课例，从而梳理、归纳、总结出线上教学的得与失。本文正是笔者在实践的基础上，结合应用学习科学与游戏化教学的相关理论，以北师大版数学五年级下册《倒数》一课为例，谈谈如何更好地设计与实施线上教学。

一、峰值体验，激发学生探究欲望

学习科学是研究教与学的跨学科领域，它研究人是如何学习的，如何有效地促进学习，它包括但不限于认知科学、教育心理学、脑科学、教育学、社会学、心理学等。将学习科学的相关理论应用于教学过程，能有效提高教与学的效率。以“峰终定律（Peak-End Rule）”为例，这是2002年诺贝尔经济学奖获得者丹尼尔·卡尼曼教授提出的，他认为：人的大脑在经历过某个事件之后，能记住的只有“峰”（高潮）和“终”（结束）时的体验，过程的体验其实是可以被忽略的。如游乐场里比较有名的游玩项目都要排很久的队，真正的游玩时间也就几分钟，但人们记住的往往不是排队等待的漫长过程，而是有趣、刺激的游玩时的几分钟甚至几秒钟。“峰终定律”被证实在多个领域有着积极的应用。事实上，在教育教学中，教师如果意识到“峰终定律”的价值，同样可以巧妙运用这条定律，创设好的峰终事件，为课堂教学带来好的学习体验，激发学生积极的数学情感。

笔者尝试在北师大版数学五年级下册《倒数》一课教学时，应用“峰终效应”。通过仔细研读教材，我们将“峰值”体验设置在了倒数概念引入环节。在这个环节中，教材给出了6道乘积为1的分数乘法计算题，其目的一是巩固分数乘法的相关知识，二是通过观察、对比、分析让学生归纳出这6道算式“乘积为1”“分子分母颠倒”这两个显著特点，并总结出倒数概念。在线上教学中，教师和学生分坐屏幕两端，作为教学要素之一“环境”与线下教学完全不同，如果习惯性按线下教学的思路，一次性给出6道计算题，让学生先算，再思和议，教学环节相对冗长，学生容易游离于课堂之外。同时，受制于网络和设备，大多数授课工具的互动效果都比较有限，小学生难以游刃有余地掌握并使用，从而影响教学效果。因此，在对此环节进行教学设计时，笔者改变了教材内容的呈现方式，将重要又相对枯燥的概念引入该环节并将其设计成一个小游戏，静态的文本动起来了，6道计算题在动感的音乐中依次呈现，学生在聊天区激烈互动，在抢答、计时、探秘等游戏元素的刺激下，“让学生计算”的枯燥练习变成了激动人心的在线互动游戏，掀起了一个课堂小高潮，给学生留下了深刻的印象。

从线上教学的实际效果来看，该设计达到了预期，学生从课堂伊始就得到了峰值体验，开始了一场奇妙的学习之旅。随着动感的音乐和实时变化的计时条，学生开始了闯关游戏，利用在线教学人人有一台终端的优势，学生参与度提高到极值，每个学生都进入全身心学习的状态，概念的引入变得更有趣味性和探究性。在师生互动和生生互动过程中，学生既能留意到互为倒数的两个乘数的“外貌特征”，还能把握倒数概念的本质，为后续的学习打下良好的基础。

二、切块呈现，分散难点聚焦重点

美国心理学家、教育学家理查德·E.梅耶在《应用学习科学》一书中，提出学习科学的三条基本原理：双重通道原理、容量有限原理、主动加工原理。他认为，“任何一个有效的学习理论都包含这三大基本原理。”在书中，他给了教师若干教学建议，其中一条为“将艰涩难懂的内容分割成学生可以掌握的若干小段”即“切块呈现”，其目标是调节基础认知加工，提高学生的学习效率。

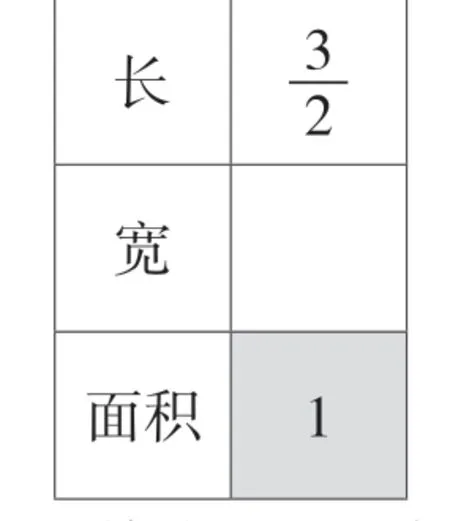
在上述案例中，教材第二、三板块的目标为“借助长方形的面积来进一步认识倒数并学习如何求解倒数”，即“倒数的进一步理解及再应用”。考虑到这两个板块的内容相关度较高，且线上教学时间比线下教学缩短了10分钟，笔者在设计时有意将这两个板块进行整合，但如此一来，难点又比较集中，学生学习难度大且不容易聚焦重点。在充分理解了教材编写特点的基础上，笔者基于学习科学切块呈现的原理并结合线上教学的特点，大胆对教材内容进行了再创造。首先，引导学生利用刚刚学到的关于倒数的经验，观察、思考、分析教师给出的下图，谈谈自己的发现，实现“借助长方形面积来进一步认识倒数”的小目标。其次，通过完善表格，引导学生观察数据，思考怎么根据“面积是1的长方形的长和宽互为倒数”这一发现求宽。最后，分类分步给出长或宽为分数、整数、小数、1这四种情况，带领学生逐一求解。在此过程中，笔者有意识地将求解重点放在“如何求一个小数的倒数”，学生自拍求解过程上传到班级群，教师全面了解学生求解思路并选择合适的探究素材与学生交流互动，从而突破教学重难点。

切块呈现，分散了教学难点、聚焦了教学重点，是比较常见的教学手段，经过教师巧妙构思、精心设计，一个个知识点被一条隐形的线牵引着来到学生面前，学生在一个个小任务的完成中，获得了学习的成就感。从学习心理学的角度来说，让学生不断地拥有成功的体验，是保持学生学习热情的有效途径，此时，若再借助班级优化大师等教学评价小软件，即时给予学生评价，特别是借助软件中的评价成长体系，就能督促学生更积极地参与学习，学生也能产生荣誉感和使命感。

三、突出结构，有目标有关联地学

美国著名心理学家、教育学家布鲁纳认为，学习的实质是一个人把同类事物联系起来，并把它们组织成赋予它们意义的结构。学习就是认知结构的组织和重新组织，就像木头、石墨、钻石的基本构成元素都是碳原子，却因为结构的不同而发生了千差万别的变化。在教学中，如果不能很好地把握本学科的本质，以有结构地教，促进有目标、有结构、有关联地学，学生的学习也会如同“木头、石墨、钻石”，形成巨大的差异。

在《倒数》一课的学习中，教材的四个环节看似独立，仔细分析却自成体系、自带结构。第一个环节引入倒数概念，解决“是什么”的问题；第二、三环节在进一步理解倒数概念的基础上，学习倒数知识的应用，解决“有什么用”的问题；最后一个环节表面上看是学习“0没有倒数”，从另一个角度理解倒数概念，但仔细思考，它是数学精确性、严谨性的体现，展示了数学之美。因此，笔者在进行教学设计时，有意放慢节奏，不满足于学生简单地回答“0有倒数”或“0没有倒数”，而是鼓励学生进行讨论，从多维度分析解释“0为什么没有倒数”，通过一个问题的解决，关联了“倒数概念”“度量本质”“乘除互逆”等学科知识，让学生意识到学科知识之间的关联，养成系统、整体、全面思考问题的习惯。

结构化教学的根本目的是帮助学生形成结构化思维，要以整体、系统的视角统筹教学设计，精心设计环节之间的过渡语言。如，“同学们，利用刚才学习倒数的经验，请你们认真观察表格，说说你们的发现”，这有利于勾连知识之间的内在联系，沟通概念学习与应用之间的内在关系。在游戏时，教师激励学生“应用新学的知识”去分析数学游戏的内涵，看到游戏和所学知识之间的关联点，引导学生从不同角度去理解数学知识。教师过渡语言的小小变化，体现的是教师对学生认知规律的尊重，帮助学生“边学边串”，学生不仅学到了系统的知识，更重要的是提升了思维和学习能力。