温“故”引问题，知“新”悟通法——以“双垂法解对角(直角)互补模型”为例

谢玲玲

(濉溪县城关中心学校 安徽淮北 235100)

一、教学设计

(一)温“故”

法国著名的数学家、哲学家笛卡尔曾经说过：“我解决过的每一个问题都成为日后用以解决其他问题的法则。”数学解题亦应如此，我们解决过的每一个问题都应为我们解决其他问题提供经验。下面以八年级解决过的一道题为例：

问题1：如图1，在△中，∠=90°，=,现将一块三角板的直角顶点放在的中点处，两直角边分别与、相交于点、。求证：=。

追问：若三角板绕旋转，与边、相交于点、上面的结论还成立吗？

图1

设计意图：借用笛卡尔的名言导入，开门见山，同时点明了本节课的主题——温“故”知“新”，其实这也是解决数学问题时经常用到的方法。从一道八年级解决过的问题出发，起点低，大部分学生都能够掌握，追问中加入了旋转，也更能体现模型的本质——对角互补。经过学生思考以及教师引导、分析其中的基本解法之一双垂法构造全等三角形的过程，使学生积累了基本的解题经验，为顺利解决后面的问题做铺垫。

(二)知“新”

问题2：如图2，在△中，∠=90°，=,现将一块三角板的直角顶点放在边上点处，两直角边分别与、相交于点、。此时，=还成立吗？说说你的理由。

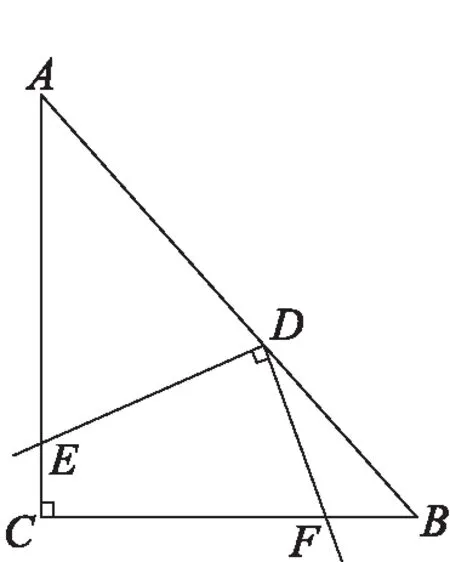
图2

问题3：如图3，在△中，∠=90°，=4,=3,现将一块三角板的直角顶点放在边上中点处，两直角边分别与、相交于点、。此时，与又有怎样的数量关系？

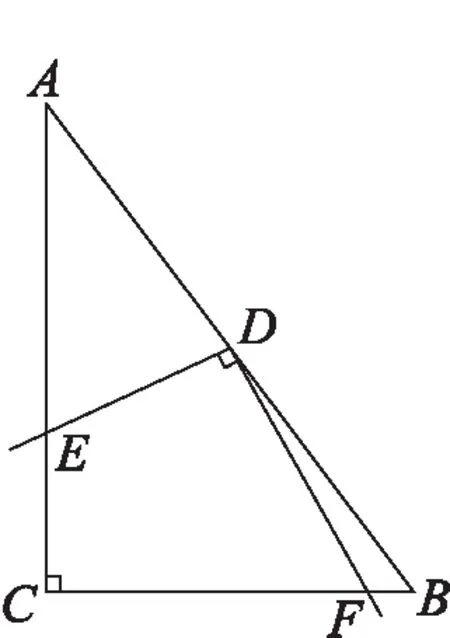
图3

设计意图：变式是数学解题教学中最重要的方式，是有意识地让学生在变化的过程中，多角度地理解问题，发现不变的内核。在问题1的基础上，问题2、问题3改变点的位置、△的形状，但核心——对角互补始终不变，目的是让学生发现变中的不变——对角(为直角)互补，并思考问题1的解决方法这里能否继续使用、得到的结论是否一致。在环环相扣的问题的引领下，让学生在探究的过程中透过问题表象感悟到模型本质，灵活掌握一以贯之的解决方法，以及数学问题研究中从特殊到一般的思路。

(三)悟通法

问题4：通过上面的研究，你能总结一下你的发现吗？

设计意图：很多时候学生在上课听懂之后，做题时仍存在很多困难，主要是因为学生没有及时将所学知识内化于自己的知识、思想方法体系中，进行融会贯通。因此，方法的归纳、总结由学生独立完成，尤为重要。特别是在学生亲身经历整个探索过程后，会水到渠成得出对角互补模型的常用解法——向两边作垂线即通过双垂法构造全等、相似三角形。事实上，对角互补在此处可得一对等角，加之作出的垂线必然能得出相似三角形，特殊的就是全等三角形。阶段性的回顾、反思能够及时反馈学生的所思所想，提高学生的归纳、综合、分析问题的能力，数形结合能力，加深了学生对模型本质的理解。

问题5：如图4，在△中，∠=90°，现将一块三角板的直角顶点放在边上点处，两直角边分别与、相交于点、。你能说说与的数量关系与哪些量有关系吗？

图4

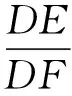
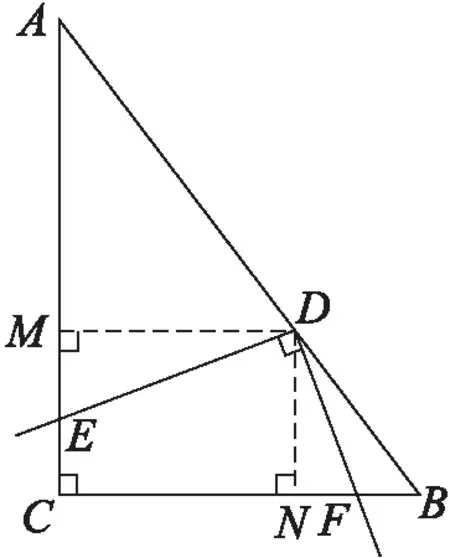
图5

问题6：如图6，Rt△，∠=90°，=4,=3。Rt△，∠=90°，点在上，交于点，交于点。当=2时，=。

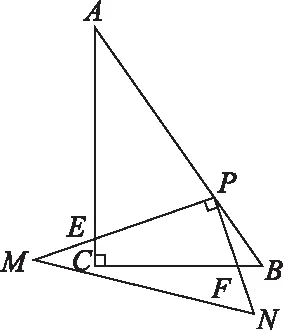
图6

图7

图8

(四)再“思”

问题7：回顾今天的整个研究思路，说说你的收获，你接下来想要研究什么？

设计意图：大部分同学在解题后便将问题弃之脑后，但解题后的再“思”恰恰是完善知识体系、优化解题方法、感悟数学思想的重要一步。当回顾整个学习过程时，学生会发现整个过程研究的都是对角是直角的互补模型，进而会思考并提出问题：当对角不再是直角时，上述方法是否可行，让学生学会在探究的过程中，发现问题、提出问题、分析问题、解决问题，真正做到学会学习、学会思考，能够“以其所知，喻其不知”。

二、几点思考

(一)关于温“故”

温“故”是为了更好地知“新”。温“故”是调用学生已有的解题经验，知“新”则是进一步完善学生的知识、方法体系。对于教师而言，学生已积累了一定解题经验，教师须能准确定位，并据此选择具有基础性、生长性、拓展性的问题进行深度挖掘、精心设计，让学生有拨云见日之感。

如本文选择的问题的起点就是八年级习题中比较经典的一题，大多数同学都能解决。在“源”题的基础上，根据波利亚的《怎样解题》中提出的解决“变化题目”的方法：普遍化、特殊化、类比以及分解和重组，采用“普遍化”的方法，将三角形的形状由等腰直角三角形到一般的直角三角形，中点也变为上的任意一点，进行变式，让学生在解决问题的过程中体会模型本质，感悟特殊到一般的思想。这样，学生不仅学习到一类问题的解决方法，更学习到研究数学问题的一般思路。

(二)关于双垂法的认识

2022年版《义务教育数学课程标准》指出：“数学是研究数量关系和空间形式的科学。”因此，对于几何对象的研究通常从位置和数量关系这两个方面展开，对角互补模型也是如此。除此之外，还应引导学生分析其中存在的基本图形之间的关系。例如，当对角是直角时(如图9)，通过向∠两边作垂线可得四边形为矩形，△与△相似。特别的，当点在∠的角平分线上时(如图10)，△和△是全等的，四边形是正方形。

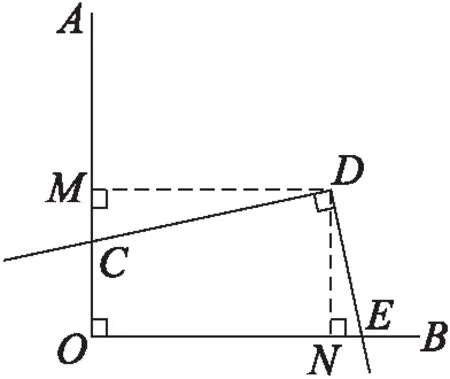
图9

图10

当对角互补但不是直角时，仍然可得△和△之间存在相似关系(如图11)；特别的，当在∠的角平分线上时，△全等于△(如图12)。

图11

图12

综上所述，在对角互补模型中，双垂法本质上就是向角两边作垂线构造相似或全等三角形，由对角互补易得、、、四点共圆，因此，在实际考查中对角互补模型也常常与圆结合考查。此类题目综合性较强、难度较大，对学生综合运用知识的能力要求较高。

(三)悟自然之法——通法

本文所选取的只是学生想得到的、易于接受的解题方法。即便是这样，让学生“悟”出通法也是存在一定难度的，只有学生亲身经历探索、归纳、总结、应用等全过程，才能体悟到不变的解法源于深刻认识模型本质。

数学解题历来有“通法”和“巧解”之分，“通法”体现的是对一般规律的概括，有助于学生理解问题本质、举一反三；“巧解”体现的则是具体问题具体分析，能够帮助学生迅速解题，二者都很重要。若从学生的角度考虑，能够想得到的、适用性广的方法才是好的方法，因此，教师还需在引导学生把握通法的同时，探究问题特殊性和普遍性的联系，培养学生思维的灵活性、创新性。

最后，温“故”知“新”也是以学定教的过程，学生并不是脑袋空空地进入课堂，而是已经具备一定的知识和能力基础，教师需要找到恰当的知识起点，才能激发学生继续探索的兴趣。尤其是习题课，学生对习题课的认知还停留在做题上，而“题海”战术只能消磨学生的个性、学习兴趣，僵化学生的思维，所以设计节奏紧凑、自然又层层深入的教学过程，能让学生体会到研究数学问题的一般思路，享受解题带来的快乐。温“故”也能系统化学生所学知识，特别是当解题遇到阻碍时，及时温“故”，也不失为一种好方法。