考虑温度效应的延安新区压实黄土全吸力范围持水和渗透特性研究*

2022-10-06张亚国王幼博李同录郭松峰

工程地质学报 2022年4期

关键词：土样渗透系数吸力

张亚国王幼博李同录郭松峰张勋梁伟

(①长安大学建筑工程学院，西安 710061，中国)

(②黄土高原水循环与地质环境教育部野外科学观测研究站，庆阳 745399，中国)

(③长安大学地质工程与测绘学院，西安 710054，中国)

(④中国科学院地质与地球物理研究所，北京 100029，中国)

0 引言

黄土作为建筑填料被广泛地用于各类建筑地基、路基及垃圾填埋场盖层当中(詹良通等，2017)。受干旱半干旱气候影响，距地表埋深2m内的黄土季节温差可达20℃以上(Hou et al.，2019)，说明自然条件下黄土地区浅层土壤温度会有较大幅度的变化。对于垃圾填埋场，监测数据显示垃圾经发酵产生的热量能使上覆土层温度高达40多度(Hanson et al.，2010)。已有研究表明温度的变化将影响非饱和土中水分迁移速率和分布特征(Hopmans et al.，1985)。如蔡光华等(2017)通过土柱试验，发现水分迁移或渗透速率随着温度梯度的增大而增大；此外土中水分会从高温势向低温势迁移，使得局部含水率增大或基质吸力增大，进而引起土体的增湿变形或干缩开裂。Romero et al.(2001)试验研究表明，相同孔隙比的土体在温度较高情况下渗透性较大；当体积含水量较高时，土体渗透性对于温度的依赖性更高。以上研究是从定性的角度分析了温度对土体持水性和渗透性的影响。要定量预测和分析温度对土体水分场和渗流场的影响，首先需要研究温度对土体的两个重要水力参数——土-水特征曲线(soil-water characteristic curve，SWCC)和渗透性曲线(hydraulic conductivity curve，HCC)的影响。

SWCC反映了非饱和土的持水性能，是表征土体含水状态与力学特征联系的重要本构关系。Nimmo et al.(1986)在不同温度下测定了不同类型土体的SWCC，发现相较于粗粒土，细粒土持水能力更易受到温度的影响，并且温度效应随着土体含水量的增大而减弱，分析认为温度是通过影响表面张力来影响土体的持水能力的。Grant et al.(1996)以热力学为基础，分析量化了温度对土体接触角的影响，并将其引入Philip et al.(1957)提出的吸力预测公式中。近年来，王铁行等(2008)和蔡国庆等(2010)针对非饱和黄土开展了研究，测定了不同温度下黄土SWCC变化规律，并提出了相应的预测方法。陈勇等(2021)研究了不同竖向应力、温度条件及干湿循环对粉质黏土持水性能的影响特征，并提出了湿-载-热耦合作用下的SWCC预测模型，为分析复杂应力和水力环境下土体持水特性提供了依据。需要注意的是这些成果中仅研究了温度对黄土低吸力段(0～103kPa) SWCC的影响，缺乏全吸力范围内SWCC随温度变化的试验结果和预测模型。

HCC反映了土体渗透系数随含水率或吸力的变化。目前考虑温度影响的土体渗透性试验研究多是针对饱和土开展(Villar et al.，2003；王媛等，2010)，而关于非饱和土HCC的试验成果还鲜有报道。非饱和土HCC主要通过瞬态剖面法确定，具体是沿土柱两侧各插设一系列张力计和水分计(两种传感器的位置一一对应)，定期量测水分从土柱上端流到下端过程中各位置的基质吸力和含水率；然后根据基质吸力剖面确定水头剖面，通过含水率变化计算单位流速，最后结合达西定律确定不同含水率所对应的渗透系数。由于试验中采用的土柱尺寸大，很难在控制土样温度的情况下进行渗透试验，这使得已有研究多是通过SWCC曲线对HCC曲线进行的理论预测，缺乏相应的试验研究。如蔡国庆等(2011)在van Genuchten(VG)模型基础上，给出相关参数随温度变化的计算公式，从而得到考虑温度影响的渗透系数函数预测方程。由于缺少非饱和渗透系数实测数据，故该模型预测的适用性仍有待验证。此外，由于瞬态剖面法所采用的张力计量程有限，通常不超过100kPa，使得目前对渗透系数的研究主要集中在低吸力段。由于课题组自行设计的试验装置实现了土柱的小型化和测试方法的精细化(张亚国等，2017)，因而可将其放置在恒温箱来严格控制试验温度；此外该装置用滤纸替代了传统方法中的张力计，故可确定全吸力范围内(0～105kPa)的土体渗透系数。

鉴于此，本文在严格控制温度的条件下，采用滤纸法及小土柱瞬态剖面法分别对20℃、30℃和40℃ 3种温度下压实黄土的SWCC及HCC进行测试。在分析土体水力参数温度效应的基础上，通过改进的预测函数对延安新区压实黄土水力特征参数进行预测。本文的研究结果进一步完善了黄土SWCC和HCC实测数据资料，也为定量分析考虑环境温度影响的黄土填埋场地水分场和渗流场提供了基础参数。

1 不同温度下压实黄土SWCC和HCC的测定

1.1 试验土样

1.2 不同温度下SWCC的测定

目前测定SWCC的常用方法主要有张力计法、轴平移法及滤纸法等，其中张力计法和轴平移法分别只能测得100kPa和1500kPa以内的基质吸力，而土体的基质吸力最高可达105kPa，因而这两种测量技术无法测得完整吸力范围的SWCC曲线。由于滤纸法量程大，理论上能测量全范围的基质吸力，因此本文采取滤纸法测定不同温度下黄土的SWCC。

将制好的环刀样放置于110℃烘箱烘干。采用滴管对烘干后土样进行配水，两个一组预配成相同含水率；为得到较为完整吸力范围内的SWCC曲线，各组土样含水率依次均匀地分布于干燥至饱和之间。将用于测定基质吸力的Whatman No.42滤纸夹在两张普通滤纸中间，以防止测试滤纸被土样污染。待土样中水分均匀分布后，将备好的滤纸层夹在相同含水率的两环刀土样之间；之后分别用保鲜膜、锡纸和石蜡依次对夹有滤纸的土样进行包裹密封，以避免土样水分散失或吸入空气中的水分；土样密封效果如图2所示。试验设定20℃、30℃和40℃作为环境温度。将全部密封土样放置于设定温度的恒温箱中两周时间，使滤纸和土样中水分达到平衡状态。

放置期间禁止打开恒温箱，以确保试验温度恒定。当平衡时间达到后，从密封样中取出上下环刀土样及Whatman No.42滤纸。考虑到滤纸质量易受环境温度影响，故在拆样过程中调节室温至与试验温度一致。注意滤纸从环刀土样间夹出后，立马将其放置在具有相同温度且事先称量好的铝盒中，整个夹取工作需在恒温箱中快速完成。每拆封一个密封样后，关闭恒温箱门，待恒温箱温度达到设定温度并恒定一段时间后再拆封下个试样。通过烘干法确定土样及滤纸质量含水率大小，环刀土样和滤纸分别用精度为0.01g和0.0001g的天平称量。

1.3 考虑温度效应的率定方程

当测定完滤纸含水率后，可通过率定曲线确定该含水率所对应的土体吸力值，但需注意标定滤纸的率定曲线时要考虑环境温度的影响。Haghighi et al.(2012)利用蒸汽平衡技术和轴平移技术标定了Whatman No.42滤纸，给出该类型滤纸在不同环境温度下含水率与吸力的关系。需要指出的是，不管利用滤纸法确定的是基质吸力(接触式)还是总吸力(非接触式)，都是通过测定滤纸从周围环境中吸水量多少来间接确定的，因而当平衡时间足够长时，基质吸力和总吸力的率定曲线是一致的(Marinho et al.，2006；Haghighi et al.，2012)。为此，Haghighi et al.(2012)充分考虑了采用盐溶液校准曲线时滤纸的水分平衡时间(试验中平衡了14d，通常为7d)，得到了适用于标定基质吸力的率定曲线。在此基础上，通过对试验数据进行拟合，得出考虑温度影响的滤纸率定曲线方程，如式(1)所示。

(1)

式中：ψ为土体吸力；Wf为滤纸的质量含水率；T为目标温度；A、B、C、D、F、G和H均为常数，具体数值见表1。

表1 率定曲线方程参数Table 1 The parameters of the calibration equation

为了进一步验证式(1)的可靠性，图3中将由式(1)预测的率定曲线与王叶娇等(2021)实测值进行了对比，发现该式能够较好地预测不同温度下滤纸含水率和吸力之间的对应关系。为此，本文利用式(1)确定了试验温度(20℃、30℃和40℃)下的基质吸力，并将其用于滤纸法及小土柱法试验中。

1.4 不同温度下HCC的测定

土样渗透系数需结合基质吸力及土样含水率变化进行计算。将每两个环刀土样中间用于测定基质吸力的Whatman No.42滤纸作为计算断面，则根据达西定律，n断面在Δt内的渗透系数k为：

(2)

式中：vw为Δt内的渗流速度；in，ave为断面n处Δt内的平均水力梯度；ΔVw为Δt内通过断面n的流量；A为水分通过的横截面面积，这里A=30cm2。

在已知滤纸含水率时，不同试验温度下土样基质吸力ψ可根据式(1)得出。将所得基质吸力数据换算为水头剖面以计算in，ave：

(3)

式中：hn-1，ti及hn，ti为ti时刻n-1断面和n断面的总水头；hn-1，ti-1、hn，ti-1为ti-1时刻n-1断面和n断面的总水头；zn、zn-1为n与n-1断面的位置(距离土柱顶面的距离)。

由于在试验过程中，水流在土柱内持续渗透，故在时间间隔Δt内通过断面n的流量ΔVw与断面以下土柱部分的水分增量相同：

(4)

式中：ΔVw为Δt=ti-ti-1时间段内通过断面n的流量；θti-1(z)、θti(z)分别为ti-1和ti时刻的体积含水率剖面。将式(3)、式(4)的计算结果和截面积A、时间Δt代入式(2)即可得到该处的渗透系数。将该位置处的渗透系数与基质吸力一一对应，即可得出各试验温度下完整吸力范围内土体的HCC曲线。

2 试验结果分析

2.1 SWCC结果分析

图5是实测黄土SWCC数据，分析发现处于不同基质吸力段的土体，其持水能力(体积含水率)对温度的敏感程度不同。温度对土体SWCC的影响更多体现在高吸力段，表现为温度升高，同一基质吸力下土体含水率降低，即持水能力降低。而在低吸力段，各温度下实测点分布基本一致，黄土持水能力受温度变化影响较小。

由图6可见，水-气交界面处表面张力随着温度升高而下降(Lu et al.，2004)。再根据Young-Laplace方程可知，表面张力在不同大小的孔径中，对基质吸力的影响程度不同。在高吸力段，水分主要存在于狭小的粒内孔隙中，基质吸力受表面张力变化的影响较大；且此时土体内的相当一部分空间被气体占据，部分气体会以气泡的形式存在于孔隙水中。这种情况下，温度升高会使得水-气交界面处的表面张力下降，同一含水率下土体基质吸力随之降低。同时土中气体以及气态水受热膨胀会占据更多的孔隙空间(谈云志等，2014)，部分液态水还会随温度升高转化成气体，进一步造成土体的含水率下降。而在低吸力段，黄土处于近饱和状态，土中孔隙几乎全部被水充满，孔隙气含量较少，且水-气交界面也多存在于粒间大孔隙中，表面张力的变化对基质吸力影响较低。因此，温度变化对土体持水能力的影响主要集中在高吸力段，对低吸力段的影响不明显。

2.2 HCC结果分析

3种试验温度下压实黄土非饱和渗透系数测定结果如图7所示。通过分析试验数据发现，土样在整个增湿过程中其渗透系数一直呈增大趋势。在试验开始时，土柱整体处于干燥状态，土体内部基质吸力达到最大。随着上部供水系统水流的持续入渗，土中含水率增加，基质吸力减小，渗透系数也开始增加；此时温度对于渗透系数的影响极其微小，不同试验温度下测得的土样渗透系数基本重合。而当基质吸力减小到一定程度时，温度对渗透系数的影响开始凸显，温度越高，渗透系数增长速率越快。对于土体渗透特性，温度主要是通过影响土中水的动力黏度来改变土的渗透性大小。如温度升高，水的动力黏度降低(图6)，流动速度加快，土体渗透性也将随之增强。但从试验数据图7来看，温度对土体渗透性的影响并没有完全体现在整个吸力范围。

当土体处于高吸力段时，孔隙水多存在于一些相互独立的小孔隙中，孔隙水没有贯通，难以流动(李喜安等，2018)，因而温度对水动力黏度的影响不会引起土体渗透性出现大的改变。同时，土体基质吸力仍处于较大水平，部分自由水由液态转变为气态，这可能进一步削弱水动力黏度对土体渗透性的影响；故高吸力段温度对渗透系数影响不明显，如图7所示。对于低吸力段土体，水分已充满小孔隙并逐渐扩散到大孔隙中，形成了贯通的渗流管道。此时水动力黏度随温度的变化成为影响土体渗透性的主导因素。由于水的动力黏度随温度的升高而减小，相应地，土体渗透系数随温度的升高而增大。

对比分析温度对压实黄土SWCC及HCC的主要影响因素，发现表面张力变化对基质吸力的影响更多体现在小孔隙中，而渗透系数受水动力黏度变化的影响则在大孔隙更明显。因此，实测黄土SWCC(图5)与HCC(图7)均出现了对温度变化敏感和不敏感的吸力区间，且分段点均处于基质吸力90kPa左右(接近1个大气压位置处)。

3 考虑温度效应的SWCC及HCC预测模型

3.1 SWCC预测模型

VG模型是拟合土-水特征曲线较为常用的模型之一，其拟合曲线能够较好地表征土体在进气压力值和趋近残余含水量状态时的平滑过渡情况(潘登丽等，2020)。模型表达式如下：

(5)

式中：θ为土体体积含水率；ψ为基质吸力；θs、a、n为预测参数，分别近似表示土体饱和体积含水率，进气值的倒数以及土-水特征曲线中间吸力段斜率大小。

蔡国庆等(2010)所提出模型表达式与VG模型相同，但在参数选取上综合考虑了温度对表面张力及浸润系数的影响。本文通过该模型，将温度作为确定各预测参数的唯一变量，对压实黄土SWCC进行数据拟合及预测：

(6)

(7)

n=n0+λn(T-T0)

(8)

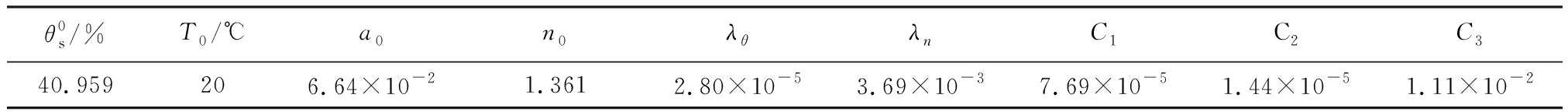
表2 不同温度下延安压实黄土SWCC预测模型拟合参数Table 2 Model parameters of SWCC of Yan’an compacted loess under different temperatures

由于40℃并非参考温度或对照温度，故利用该温度下实测数据进一步对预测公式的可靠性进行验证，结果如图8所示。可以看出40℃预测结果与实测的SWCC数据点吻合较好；且对比40℃预测线与20℃及30℃拟合线，发现三者在高吸力段表现出较为明显的差异。

3.2 HCC预测模型

目前主要是通过统计模型对渗透性曲线HCC进行预测。具体而言，当SWCC已知时，可依据Young-Laplace方程得出任一基质吸力下土体被水充满孔隙时的最大孔径；再以孔径分布函数作为中间函数，推导土体吸力与渗透系数之间的关系，即渗透性曲线HCC。李华等(2020)在测定了甘肃地区黄土HCC后，利用多种统计模型对其进行了预测；结果表明预测结果仅在低吸力段与实测数据相接近，当基质吸力增大到一定程度后，统计模型得出的渗透系数偏小。分析其原因认为，对于黏性土，当土体含水率较低时(对应SWCC的高吸力段)，孔隙中的水主要以结合水的形式存在，因而基于毛细理论的孔径分布统计模型不再适用。鉴于此，本文根据温度影响下黄土HCC的变化规律，采取分段函数的形式建立预测模型，在低吸力段采用统计模型对渗透系数进行预测，高吸力段通过幂函数进行预测。结合图7所示各试验温度下实测渗透系数结果，可将预测公式的分段点定于土体基质吸力约处于90kPa处。

当基质吸力ψ<90kPa(低吸力段)时，采取统计模型对黄土HCC进行预测。将用于预测SWCC的VG模型(式5)代入Mualem(1976)提出的统计传导率模型中，可得到计算土体非饱和渗透系数的表达式：

(9)

式中：kr为土体相对渗透系数，定义为任意基质吸力下土体渗透系数k与饱和渗透系数ks的比值；ψ为基质吸力；a与n均为SWCC拟合参数；如ks、a、n已知，即可得出一条完整的土体渗透曲线。在考虑温度影响情况下，a与n可利用式(7)和式(8)以及表2中的拟合参数直接进行计算，但饱和渗透系数ks还需结合实测数据进行预测。

Romero et al.(2001)将温度对土体饱和渗透系数的影响归纳到一个经验系数βT上，βT可由两种不同温度下实测渗透系数计算得到。对于不同土体类型或不同参考温度，βT数值不同。如式(10)所示，ks(T0)为参考温度T0下土体饱和渗透系数，ks(T)为目标温度T下土体饱和渗透系数。

(10)

在式(10)基础上，利用变水头试验实测出20℃、30℃和40℃下黄土饱和渗透系数，并取20℃、30℃实测结果进行计算，得βT=5.36×10-2。将βT、T0、ks(20℃)代入式(10)，可得出不同温度下饱和渗透系数的预测值，结果如图9所示。由图可见预测的40℃时饱和渗透系数与实测结果吻合较好。

当基质吸力ψ≥90kPa(高吸力段)时，引入幂函数对黄土HCC进行分段预测，幂函数形式如式(11)所示：

k=cψd

(11)

式中：k为渗透系数；ψ为基质吸力；c和d为预测参数。取不同试验温度下ψ≥90kPa范围内实测非饱和渗透系数进行数据拟合，得到c=2.584×10-8，d=-1.362。

将式(9)、式(10)和式(11)按照分段函数形式进行整合，可得出温度影响下黄土全吸力段HCC预测函数：

(12)

式(12)中：参数a、n需结合表2中SWCC预测参数及目标温度T进行计算；T0、ks(T0)、βT、c和d均为常数预测参数，其值如表3所示。