考虑初始含水率分布的覆盖层边坡非饱和入渗过程与稳定性计算方法*

史振宁 戚双星 刘登生

(①长沙理工大学公路养护技术国家工程实验室，长沙 410114，中国)

(②长沙理工大学土木工程学院，长沙 410114，中国)

(③中交(天津)生态环保设计研究院有限公司，天津 300450，中国)

0 引 言

覆盖层边坡特指底部为中风化或弱风化基岩，上部覆盖有较松散坡积土的一类边坡，广泛分布于我国华东、华南等地区，在云贵川等地也有大量分布。尤其是在浙江西部地区主要以沉积岩为主，极易形成全-强风化覆盖层边坡。对于覆盖层边坡而言，上覆土层土质较为松散，强降雨所导致的入渗过程会使覆盖层内部含水状态发生改变，从而对边坡稳定性产生明显影响。已有学者明确指出，基岩风化形成的残坡积覆盖层滑坡是浙江地区土质滑坡中最主要的滑坡形式，约占浙江地区滑坡总数量的80%左右(王洲平，2001；俞火明等，2008；岳丽霞，2012；Ma et al.，2015)。

为此，众多学者针对覆盖层边坡非饱和入渗过程以及稳定性变化开展了许多有益的研究。在边坡降雨入渗特性方面，Montrasio et al.(2009)在研究中假定雨水在松散覆盖层边坡内部会迅速渗流至底部，导致地下水位上升，其入渗过程对边坡稳定性影响较小。但Sung (2017)的研究成果表明降雨入渗过程中土体内部会形成湿润锋，可使边坡内部形成潜在滑动面，导致边坡失稳；Trandafir et al.(2008)研究得出日本三重县残积土边坡内部孔隙水压力沿高程分布呈上部较低，底部较高的线性分布，且降雨入渗深度随降雨总量增加而增加，并与雨型密切相关。潘俊义等(2018)根据野外模拟人工降雨试验成果，指出不同雨强条件下的黄土边坡入渗深度均呈现坡脚最深、坡顶次之、坡中最浅的规律。Godt et al.(2012)对美国西雅图某坡积土边坡进行监测，得到了约100id范围内的降雨量以及边坡体积含水率和孔隙水压力的变化规律。詹良通等(2003)对湖北枣阳市某引水渠膨胀土边坡进行了体积含水率以及表面位移现场监测，发现对于膨胀土边坡而言，降雨入渗的影响多在2im之内，揭示了膨胀土多发浅层滑坡的主要原因。

在边坡稳定性分析方面，蒋中明等(2018)给出了可考虑不同类型暂态水压力的覆盖层边坡稳定性计算方法。刘顺青等(2019)指出边坡块石含量以及分布会对边坡稳定性造成明显影响，但该研究成果没有考虑降雨入渗的作用，忽略了对边坡安全影响最重要的因素。马世国等(2015)的研究成果表明强降雨入渗期间，浅层边坡潜在的滑裂面沿湿润锋和基岩面近似呈双折线形；覃小华等(2017)进一步考虑了层状边坡的渗透系数变异性，结合蒙特卡洛法，建立了考虑饱和渗透系数变异性的基岩型层状边坡稳定性可靠度计算模型，但上述研究对含水率的初始分布仍采用整体均一性假设，与大量试验和现场观测数据不完全相符。由此可见，目前针对覆盖层边坡的渗流特性分析中对初始含水率分布的假定仍缺少试验验证，在边坡稳定性分析中较少考虑非饱和浸润线对稳定性的影响，边坡稳定性对各类影响因素的响应程度也鲜见讨论。

综上所述，本文利用自主设计的土体降雨入渗试验装置，分析了覆盖层边坡在自然状态下的初始含水率分布规律以及降雨入渗规律。在此基础上提出了一种新型边坡稳定性计算方法。根据此方法对典型覆盖层边坡稳定性对多种影响因素响应的敏感程度开展了研究。所得成果可对同类边坡稳定性分析具有参考意义。

1 初始含水率分布与非饱和入渗过程

为探究覆盖层边坡的初始含水率分布以及在降雨入渗条件下含水率沿高程分布与演化规律，设计了室内降雨入渗实验装置，如图1，图2所示。利用该装置首先研究覆盖层土体初始含水率分布，然后开展降雨入渗试验，分析土体各个高程处的含水率变化规律(曾铃等，2018)。

降雨入渗试验方案如表1所示。在降雨入渗试验之前，首先使模型桶中的填土达到饱和状态，然后打开模型桶底部的排水孔，使土中的水分自然流出。当含水率长期不变时(每天含水率变化小于1%)，则认为土体达到了稳定的初始状态。此时记录各个测点的含水率即为自然状态下覆盖层边坡的初始含水率分布状态。此时关闭模型桶底部排水孔，然后进行模拟降雨，试验所设计降雨强度为6.6×10-6m·s-1(小时降雨量23imm，为暴雨级别)。在降雨入渗过程中，每5min记录一次各个测点的体积含水率。

表1 试验方案Table 1 Test scheme

根据笔者前期研究成果(史振宁等，2020)可知，土体在自然状态下初始含水率分布规律为随高程增加，含水率逐渐下降，如图3所示。因此，可建立描述土体内部含水率沿高程分布规律的反比例函数模型，如式(1)所示。

ω∈[B，ωs]，hw∈[0，H]

(1)

式中：h为土层计算高度；ω为覆盖层土体体积含水率；A为初始含水率分布参数；B为初始状态下土体表面含水率；hw为地下水位；ωs为覆盖层土体饱和含水率；H为覆盖层总厚度；α、β为初始含水率分布修正系数，由式(2)，式(3)表示，其中K值可由式(4)得到。

(2)

(3)

(4)

将式(1)反向推导即可得到土体初始含水率沿高程分布的反比例模型，如式(5)所示。

(5)

由于在试验过程中模型底部处于不透水状态，根据Mein-Larson理论，当降雨强度小于饱和渗透系数时湿润锋深度由总降雨量控制，如式(6)所示：

I=pt=zw(ωw-ωi)

(6)

本研究在上述理论基础上，考虑若降雨强度小于渗透系数时，湿润锋高程可通过式(7)～式(9)计算得到：

(7)

(8)

(9)

式中：z为湿润锋高程(从地下水位至湿润锋处的高度)；I为总入渗量(降雨强度乘以降雨时间)；ωw为与降雨强度相对应的土体表面含水率，从式(9)中可以看出，式两侧均有z变量，属于Alnx+Bx+C=0类型的方程式，无法通过直接解方程得到z的值，只能通过迭代法对z进行计算。通过数学证明可知，该函数为定义域上的单调函数，必有至多一个实根，并且该函数在定义域范围内可取到正负值，可见该方程必有一个实根。因此该函数可采用迭代法进行近似取值，如式(10)所示：

(10)

当│zn-zn-1│<10-5时，则认为迭代结束，此时的zn值即为在总入渗水量为I的条件下，湿润锋的高度，H-zn即为降雨入渗深度。当湿润锋的深度达到地下水位的位置后，入渗的雨水进入地下水中，在不考虑土体排水的情况下，地下水位随之上升。此时边坡表面的含水率仍然保持不变，土体含水率由底部向上逐渐达到饱和。根据水量守恒原理可以推导出降雨导致地下水位上升的过程，如式(11)所示。

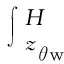
(11)

(12)

在求解hw时，应采用上述迭代法进行计算。当hw超过zωw时，则采用式(13)计算hw高度。

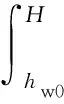
+(hw-hw0)(ωsat-ωw)

(13)

根据上述研究得到如图4所示的简化模型可知，随着降雨时间增加，降雨入渗深度hωw逐渐增加，最终引起地下水位上升。对比试验的结果(图5)(曾铃等，2018)可知该模型与试验结果基本一致。

2 非饱和土抗剪强度

Vanapaui et al.(1996)采用双应力变量对非饱和土的应力状态进行描述，提出了考虑双应力变量的抗剪强度理论公式，如式(14)所示。

τff=c′+(σf-ua)ftanφ′+(ua-uw)ftanφb

(14)

式中:c为表示非饱和土的有效黏聚力；(σf-ua)f为剪切面上的净法向应力；ua为剪切面上的孔隙气压力；φ为与净法向应力状态变量(σf-ua)f有关的内摩擦角；(ua-uw)f为破坏时在破坏面上的基质吸力；φb为抗剪强度随基质吸力(ua-uw)f而增加的速率。该理论指出，对于非饱和土而言，抗剪强度不仅受有效应力的影响，同时还会受到土中基质吸力的影响，影响幅度与tanφb有关，因此可将非饱和土抗剪强度拓展至三维包络面，如图6所示。

对于参数tanφb而言，Vanapalli et al.(1996)将其采用式(15)进行表示。

(15)

式(14)中的基质吸力可通过式(16)得到。

(16)

将式(15)、式(16)代入式(14)中，且不考虑含水率对内摩擦角的影响(张钧堂等，2016)，可得到如式(17)所示的土体抗剪强度分布规律。

(17)

3 边坡稳定性计算方法

许多学者在边坡稳定性分析中，根据边坡浅层滑坡的特点设计了简化的稳定性计算方法(Shin et al.，2013；庄建琦等，2013；贺可强等，2017)。该种计算方法假设边坡为半无限空间体，底部为基岩，上部为覆盖层土体，边坡滑动面位于覆盖层土体中，与基岩面平行。降雨入渗的湿润锋或地下水位也平行于基岩层，这样的假设较为符合覆盖层边坡的工程实际和破坏形式，并且在计算过程中可以简便地将降雨入渗以及地下水位变动引入稳定性计算中。该种方法已经得到了较多学者的应用。如Tran et al.(2017)均采用此种假设计算了降雨入渗时边坡的稳定性变化规律(Godt et al.，2012；Antinoro et al.，2017)。可见该方法切实可行，并且易于广泛应用于工程实践。本研究开展稳定性分析时同样采用上述假设，如图7所示。由于不同高程处的含水率不同，浸润土体所受重力计算方法也有所不同，因此首先分析不同位置处的浸润土体所受重力计算方法。

(1)降雨入渗情况下：考虑拟定滑动面位于覆盖层边坡浸润线上部的情况，此时土体处于非饱和状态，没有孔隙水压力作用，浸润土体的重度如式(18)所示：

W=[ωqrw+Gs(1-n)](h-hs)Δs

(18)

考虑拟定滑动面位于浸润线下部的情况，此时土体仍处于非饱和状态，没有孔隙水压力作用，浸润土体所受重力应考虑上部浸润状态以及浸润线以下至滑动面以上的含水状态，如式(19)、式(20)所示。

W=Gs(1-n)(h-hs)Δs+ωqrw(h-hq)Δs

(19)

(20)

(2)地下水位上升情况下：考虑拟定滑动面位于地下水位以上的情况，此时滑动面上部土体含水率一致，仍为非饱和状态，含水率可视为是等降雨强度含水率，重度计算与式(18)相同。考虑拟定滑动面位于地下水位以下，此时滑动面上部存在饱和区域，因此饱和区域水的作用按照孔隙水压力的方式计算，在计算滑面上部浸润土体所受重力时并不再考虑浮重度，如式(21)所示。

W=Gs(1-n)(h-hs)Δs+ωqrwΔs(h-hw)

(21)

式(18)～式(21)中：W为滑动面上部土条重；Gs为土颗粒重度；ωq为等降雨强度；含水率rw为水重度；n为土体孔隙率；h为覆盖层厚度；hs为潜在滑动面高度；Δs为条块底部宽度；hq为降雨湿润锋深度；hw为地下水位高度。在得到滑动面上部的浸润土体所受重力后，即可针对滑动面进行受力分析。边坡稳定系数计算方法如式(22)～式(26)所示：

(22)

Td=Wsinβ+F

(23)

Ts=τ

(24)

F=γw·sinβ·cosβ·hw·Δs

(25)

N=Wcosβ

(26)

式中：Ts、Td分别为覆盖层边坡潜在滑动面处的抗滑力与下滑力；β为覆盖层边坡倾角；F为渗流力；N为滑动体底面法向力；C为总黏聚力；各参数的作用点以及方向如图7所示。总结上述计算方法，可以得到降雨入渗条件下覆盖层边坡不同位置滑动面的稳定系数计算方法。(1)在降雨入渗情况下，拟定滑动面位于湿润锋上部时边坡稳定性可根据式(27)算出。

(27)

当拟定滑动面位于湿润锋下部时边坡稳定性可根据式(28)算出。

(28)

(2)在地下水位上升阶段时边坡稳定性可根据式(29)算出。

Fs=

(29)

根据不同的降雨入渗过程，分别采用以上三式即可计算得到覆盖层边坡在不同降雨入渗状态下，不同层位处的稳定系数。

4 覆盖层边坡稳定性影响因素分析

对于覆盖层边坡而言，土层厚度、坡度以及土体持水能力等都是影响其稳定性的重要因素(冯杭建等，2017)，本文前述内容已经详细给出了覆盖层边坡稳定性的计算方法，事实上覆盖层边坡稳定性对不同因素的敏感性有所不同，不同条件下导致边坡失稳的主控因素也有所差别。为进一步分析不同失稳诱因对覆盖层边坡稳定性的影响特性，设计计算方案如表2所示，土质参数如表3所示。

表2 边坡稳定系数计算方案Table 2 Calculation scheme of slope stability

表3 计算用土质参数Table 3 Soil parameters for calculation

4.1 覆盖层厚度影响

在影响降雨条件下边坡稳定性的诸多因素中，覆盖层边坡的厚度是影响等降雨量条件下边坡内部含水率分布的重要因素之一。设计方案I(表2)分析不同厚度覆盖层边坡在不同降雨时间下的渗流过程以及相应的稳定性变化规律。

从图8中可以看出，在相同的降雨总量前提下，随着覆盖层边坡厚度的增加，土体内部的含水率分布明显不同，当覆盖层土体厚度为1im时，随着降雨的持续，雨水不断入渗至边坡内部，由于土体厚度较小，当降雨达到160min后，地下水位已经开始上升，当降雨达到240min后土体已经整体达到饱和状态。当覆盖层厚度为2im及以上时，240min的降雨量已经不足以导致地下水位上升和边坡土体饱和，整体入渗深度为1.5im。受降雨入渗的影响，边坡的稳定系数也有所变化，从图8a中可见在初始状态下边坡稳定系数整体较大，在覆盖层底部的最小值为2.8。随着雨水不断入渗，在湿润锋处的稳定系数出现了突变现象，导致湿润锋上部的土体稳定系数出现了明显的下降。当降雨入渗致使地下水位上升后，湿润锋处的稳定系数也出现了突变，在湿润锋下部区域的边坡稳定系数明显下降。而当土体达到整体饱和后，各个位置的稳定系数均达到最小，对不同高程处的稳定系数进行比较可知最小值仍处于覆盖层最底部。从图8b～图8c中还可看出，对于覆盖层厚度超过2im的边坡而言降雨入渗不会导致地下水位上升，而在湿润锋处仍会出现稳定系数的突变现象，但由于边坡厚度较大，降雨对覆盖层底部的稳定系数影响较小。

综合分析不同厚度覆盖层边坡在相同降雨入渗条件下的含水率分布以及稳定系数分布可知，在降雨强度相同的条件下，随着覆盖层厚度的不断增加，湿润锋的入渗深度基本保持不变，湿润锋距底面的距离越远，对底面含水率的影响越小。如图9所示，随着覆盖层厚度的增加，边坡初始状态下的稳定系数由2.8下降至1.09，呈现逐渐减小的规律。与此同时，当覆盖层厚度为1im时，最小稳定系数随着降雨时间的增加由2.8降至1.46，而当覆盖层厚度达到4im时，最小稳定系数随着降雨时间的增加由1.09降至1.07。由此可见，随着覆盖层厚度的增加，降雨时间对稳定性的影响也越来越小。呈现上述变化规律的主要原因为，随着覆盖层厚度的增加，土体自重也同时增加，而土体的自重在下滑力中占据了主要部分，覆盖层越厚，降雨对土体自重的影响也越小。并且覆盖层越厚，降雨越难以渗入至覆盖层底部，因此对稳定系数的影响也越小。

4.2 覆盖层土体含水率分布参数影响

根据上节研究可知，不同土质具有不同的含水率分布参数，一般而言，初始含水率分布参数越小，土体越接近砂土，初始含水率分布越接近“L”形，而初始含水率分布参数越大，土体越接近黏土，初始含水率分布越接近直线形。可见初始含水率分布参数对土体的渗流特征也有着明显影响，进而也会对边坡稳定性造成影响。因此本节根据计算方案Ⅱ探讨了覆盖层初始含水率分布参数对覆盖层边坡渗流过程以及稳定性变化的影响。

从图10中可知，不同土质的初始含水率分布状态有所不同，分布参数偏小时分布曲线更接近“L”型，随着分布参数值增加，分布曲线更接近于斜线型。受含水率分布影响，边坡稳定系数也随分布参数的增加而减小。如图10b所示，当经过80min降雨后湿润锋逐渐入渗至边坡内部，在相同的降雨时间条件下，随着含水率分布参数的增加，湿润锋位置不断下降，湿润锋处含水率的突变幅度也有所下降，相对应的稳定性突变位置也随着分布参数的增加而下降，突变幅度也随之减小。当降雨达到160min后，边坡内部湿润锋持续下降，含水率分布参数为2的粉质黏土类边坡由于初始含水率较高，已经出现了地下水位上升现象，相对应的边坡稳定性也出现了大幅下降，降雨时间达到240min后，分布参数为0.002和0.02的边坡湿润锋持续下降，而分布参数为0.2的边坡也开始出现地下水位上升，相应的边坡稳定性也不断下降。

可以看出，初始含水率分布对后续的渗流过程以及稳定性变化规律有着明显的影响，随着初始含水率分布参数值的增加，土体初始含水率越接近线性分布，边坡底部的稳定系数也逐渐降低。这是由于同样的降雨量条件下，当初始含水率分布参数较大时覆盖层边坡内部水量较多，重度较大，与此同时还会导致覆盖层地下水位上升，从而对边坡底部产生孔隙水压力以及渗流力，大幅降低边坡稳定性。从图11中可知，初始含水率分布参数为0.002和0.02时的稳定系数变化不明显，但初始含水率分布参数为2时，边坡稳定性则迅速下降。在降雨时间较小时，初始含水率分布参数对最小稳定系数的影响差异并不明显。而当降雨持续较长时间，累计降雨增加时，初始含水率分布参数对稳定系数的影响幅度逐渐增加。

4.3 边坡角度影响

边坡角度是影响边坡稳定性最为明显的因素。在较为陡峭地区的覆盖层稳定性明显小于地势平缓地区。在本文的假设中，降雨垂直入渗，高程方向与水平方向垂直，边坡角度不会对渗流特性造成影响，但边坡倾角增加会导致平行边坡方向的重力分力增加，垂直于坡面的正应力分量减小，进而导致抗滑力下降，下滑力增加，引起边坡失稳。本节针对边坡角度对稳定性的影响分析如方案Ⅲ所示，边坡渗流规律见图8b。

从图12中可以看出，当边坡倾角为20°时，边坡整体稳定系数较大，最小值为3.27，在湿润锋处的变化量也较大，当倾角为30°时边坡各个位置处的稳定系数均减小，最小值降至2.23。当倾角为45°时，边坡各处的稳定系数进一步缩小，最小值降至1.58。当边坡倾角为60°时边坡各位置稳定性降至最低，最小稳定系数降至1.29。可见随着边坡角度的增加，各位置的稳定系数均不断下降。

图13为不同降雨时间条件下，边坡角度对覆盖层边坡稳定性的影响变化规律。从图中可以看出在初始状态下，边坡角度增加所引起的最小稳定系数下降幅度最大，但是最小稳定系数仍较大。随着降雨时间的增加，各个角度下的稳定系数均明显下降，但随角度增加稳定系数的下降幅度也相应减小。

5 结 论

(1)研发了一种土体降雨入渗实验装置，根据实验结果得到土体在自然状态下的初始含水率分布可采用反比例函数进行描述，并基于此建立了降雨入渗过程中土体含水率分布解析计算方法。

(2)给出了覆盖层边坡稳定性计算方法。根据该理论得到在降雨入渗过程中，不同位置的稳定性会在湿润锋处发生突变，但一般而言最小稳定系数所对应的滑动面位于土体与基岩的交界处。在相同降雨强度条件下，降雨时间越长，越容易发生深层失稳，降雨时间越短越容易发生浅层失稳。

(3)在相同降雨量条件下，随着覆盖层厚度的增加边坡初始稳定性下降，且降雨入渗对稳定性的影响越小。在相同降雨量条件下，边坡稳定性随着初始含水率分布参数的增加而下降，随着降雨时长的增加，初始含水率分布参数对边坡稳定系数的影响更为显著。初始状态下，边坡稳定性最大，边坡角度增加所引起的最小稳定系数下降幅度最大，随着降雨量的增加，边坡稳定性受角度影响越小。