以反思性思维的发生、发展为线索进行概念课教学
——以“平方根”教学为例
2022-10-06徐丽君
徐丽君,李 明
(桐庐县城关初级中学,浙江杭州,311599)
初中教师在数学概念教学中,主要有两种认识:一是强调概念的辨识与应用;二是强调以概念为中心的相关数学知识解析.两种认识下的课堂共性是以学生认知与新概念交集设置问题情境,其后风格迥异.前者淡化学生思维的起点,设计的教学表达方式倾向于习题化,造成学生对概念缺乏理性认同,增加后期学习中出现认知混淆的风险.后者由于强调知识之间的逻辑关系,课堂有强烈的“数学味道”,但学科本位一定程度上对学生反思性思维发展过程中的痛点、盲点、堵点选择性忽视,导致学生的主动探究愿望不强烈,获得感较低.反思性思维是对某个问题进行反复的、严肃的、持续不断的深思.从根本上看,学习完全是一种反思性活动.在概念课教学中,以学生反思性思维的发生、发展为纲,以概念相关知识之间的逻辑性为目,纲举目张,突出思维过程中的主动获得,从而达成较好的学习体验.本文以“平方根”教学为例对此作些探索.
1 反思性思维要素分析
1.1 起点:从哪开始想

1.2 痛点:实在想不出
开平方是平方的逆运算,该逆向思维类似于“已知某数的绝对值求这个数”.把“求一个正数的平方根”这一问题回到思维起点(注意并不等同):已知某个正数的平方,求这个正数.学生的已有经验是:已知正方形的面积求正方形边长.优先选择平方数作为被开方数,一方面体现开方是一种运算,以便学生感悟互逆;另一方面符合从特殊到一般的认知规律.但对大部分同学(乘方运算不熟练的同学更加),从42=16易,142=196难,更难的是看到196,还要想到196不仅是14的平方,还是-14的平方,何其难!虽然可以通过分解:196=22×72=(2×7)2=142求得196的正平方根,但分解过程往往涉及后续积的乘方相关运算,同时分解运算需要较多精力投入,不利于思维聚焦.由此,课堂不宜出现繁杂的平方数(《义务教育教学课程标准(2022年版)》明确规定带分数不涉及乘方、开方运算),同时需要在前期积累对常见的平方数的感觉,这个感觉就是数感.
1.3 盲点:实在没想到
对平方数有了感觉,学生被问到:哪个数的平方等于9时,通常脱口而出:32=9,很难想到(-3)2=9.更鲜有人思考过:除了(±3)2=9还有没有其他数的
平方也等于9?思维盲区往往是惯性思维的负迁移.思维盲点有必要由教师点亮,并在前期(如上一章)学习做好铺垫.可以回到思维起点“面积为9的正方形的边长一定是3吗?”学生不难理解:边长大于3,则面积大于9;边长小于3,则面积小于9;当且仅当边长等于3时,面积等于9.事实上,面积是边长的二次函数且是函数图象的右半支,函数值与自变量的值一一对应;当去除正方形背景后(即某数的平方等于某个正数),每一个正的函数值对应两个互为相反数的自变量的值.可见,思维盲点审视可以回归思维起点,同时可以渗透数学概念之间的逻辑关联.
1.4 堵点:有点想不通

2 教学设计
【模块1】准备:培养平方数数感,以便课堂思维聚焦
(1) 计算:02,12,22,…,152
(2) 计算:(-1)2,(-2)2,…,(-15)2
设计意图:对薄弱同学,通过常见数的平方,熟识常见平方数.规律也蕴含其中,如:互为相反数的平方相等;分数的平方即分子分母分别平方再相除;若底数小数点向左(或右)移动1位,则幂的小数点向左(或右)移动2位;底数的绝对值越大则二次幂越大.第(1)小题是基础,是所有相关发现的思维起点.课堂上不一定生成这些结论,学生有所感悟即可.
【模块2】起点:创设正平方根情境,建立思维发展起点
(1) 正方形的面积为9,边长是.
(2) 写出所有分别满足下列条件的数:
① 某数的平方等于9,这个数是;
② 某数的平方等于0,这个数是;
③ 某数的平方等于-4,这个数是.
(3) 结合(1)(2),师生合作解析、文字叙述平方根概念(顺势导出正平方根、负平方根、0的平方根).
设计意图:第(1)问通过经历正方形面积与边长的互逆运算,体会平方根的产生源于实际需求,第(2)问经历已知指数和幂求底数的过程,一方面领会与“平方”的互逆,另一方面体会研究平方根是数学发展的需要.同时第(1)与第(2)①的思维冲突,激活数学思维,思考要严肃、解答要完备:正数的平方根有两个且互为相反数.思维发展来看,先求正平方根,再写负平方根;求正平方根即已知正方形面积求边长.注意:第(1)问师生需共同体会边长有且只有3,从而为第(2)①有且只有±3作铺垫,突出平方根概念的完备性.第(4)问板书如下(为符号化做准备):
∵32=9,(-3)2=9即(±3)2=9
∴9的平方根是±3.
【模块3】发展:特殊到一般,数感到符号感
(1) 正方形的面积为3,边长是;
(2) 3的正平方根是,负平方根是,平方根是.
设计意图:通过思维冲突、符号演化、例题示范,深刻体会平方根符号化的必要性、合理性、简洁性.从平方数到开不尽方的数,符合学生从特殊到一般的认知规律.(1)问的符号演变如下图(动画演示):

∵32=9,(-3)2=9即

∴9的平方根是±3,即

∵(±3)2=9

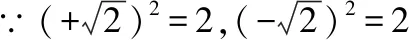
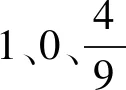
【模块4】内化:思维个性化,新的起点.
小结:板书小结,如下图.
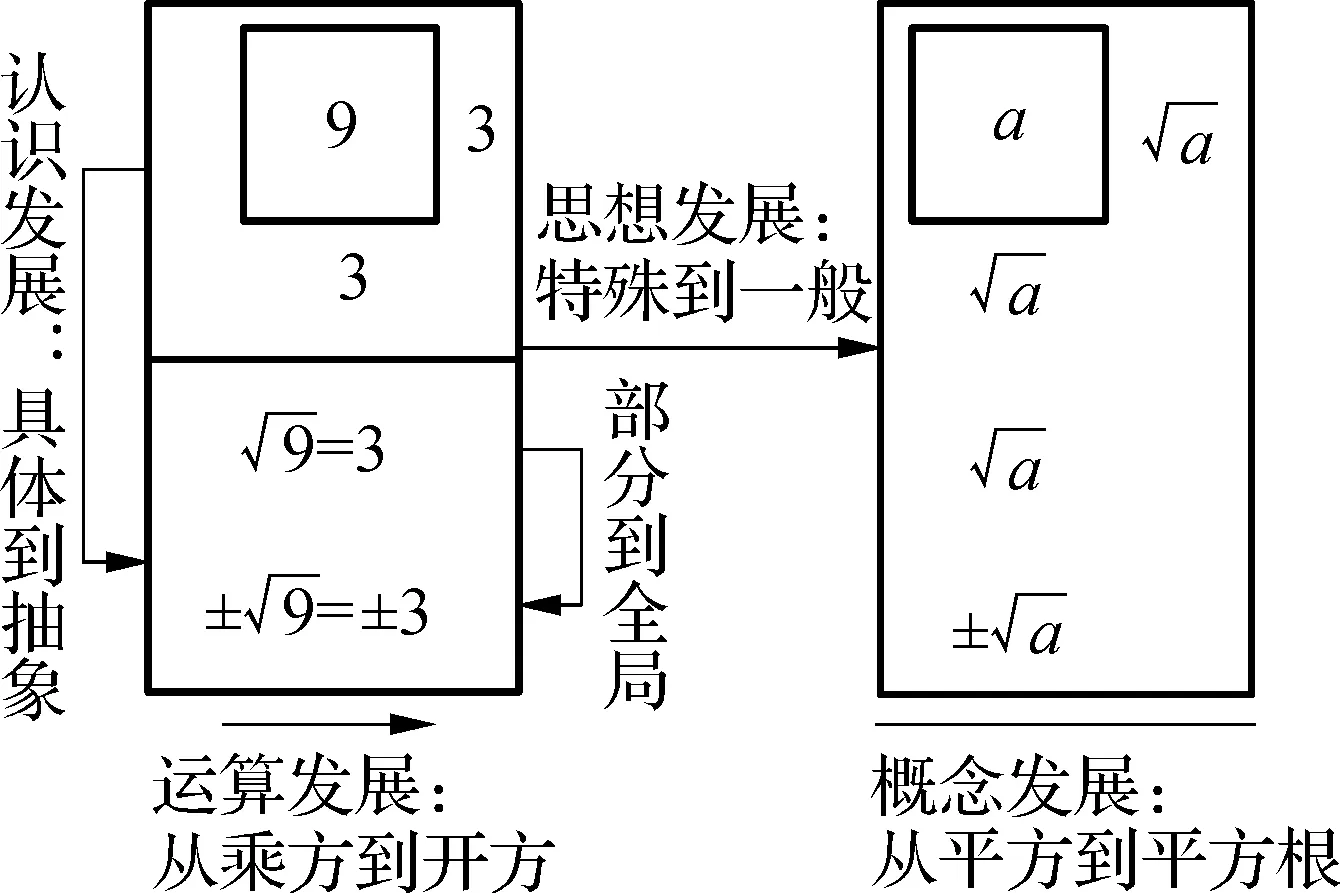
设计意图:利用课堂生成的板书,师生回顾思维发展过程关键节点.教师从知识技能、思想方法两方面引导,教师主导,共同感悟.
3 实践感悟
数学是思维的科学,数学课堂是思维的课堂.教学表达形式既要重视数学知识的逻辑,更需关注学生学习的逻辑——反思性思维的发生、发展.以反思性思维的发生、发展为主线即以学习者的学习逻辑为纲,引导学习者主动理解、应用概念,生成数学知识技能并在过程中学会数学思考.
3.1 理解学习的本质即反思性活动,积累反思性思维要素分析经验
并不是每一个数学概念的学习都有思维(指反思性思维,下同)痛点、盲点、堵点,思维起点也因人、因班而异.思维起点的确定与概念相关知识的解析、班级整体的数学素养密切相关,素养越高越倾向于“数学化”,相反则倾向于“生活化”.如平方根概念教学中,思维起点可以是“已知正方形面积求边长”,也可以是“乘方的三要素:底数、指数、幂,已知二者求第三者”.另外,随着课堂的行进,知识技能的掌握,思维也在发展,学习个体的思维起点也在动态变化,教师应鼓励学生的个性化合理思维,绝不能有“一定要这样想”的想法跟言语、感情表露.
3.2 关注学生群体思维的动态变化,领悟模块组合之“法”
以反思性思维的发生、发展为主线的概念课教学需要预设,包括准备、起点、发展、反复、内化五个模块.五个模块并不是缺一不可,如:平方根中的“准备”模块,如果学生对平方数已经有了足够的数感,这一模块自然可以省略.课堂应“顺”着学生思维的发展行进,故五个模块在课堂中的行进顺序也不是非得这样,甚至可以穿插进行,如:平方根教学中的“发展”模块,在平方根的符号生成后,就可以用不同形式的呈现方式引导学生反复思考,以利于“符号感”的生成.模块之间的灵活组合需要教师关注学生群体的思维发展变化,并作出判断.
3.3 注意教材对于学生思维的留白与冗余,以生为本是概念教学设计之“道”
浙教版每一节教材的呈现都有强烈的反思性思维味道,充分考虑普遍的学生认知特点.但教材与课堂不同,教材一览无余,课堂徐徐展开.一览无余,虽能面面俱到,但易点到即止,难判轻重;徐徐展开,虽有利思维,但易缺失目标,偏颇重心.如此,教师对教材的再创作成为必然.进行再创作,教师一方面须对与概念相关的知识逻辑了然于胸,不仅要有全局观、整体观、还要有高观点;另一方面须对学生的现有认知基础、学习特点一清二楚.初中阶段,以学生的学习逻辑为主线设计教学要注意教材中的素材呈现之于学生思维的留白与冗余.如“平方根”中,面积为1.44的正方形的边长是多少?对于大部分普通孩子而言,此处有大量留白:正方形的面积公式如何?哪个数的平方是144?哪个数的平方是1.44?面积144之于1.44的关系如何与边长有联系?(见本文第3页【模块一】)教师要思考的是:对与我的孩子们,哪些思维留白是需要做填充的.同样,“平方根”中也有信息冗余(因人、因班而异),本节课共有10个新术语:平方根、二次方根、正平方根、负平方根、根号、负根号、正、负根号、被开方数、开平方、算术平方根.新术语在课堂中的高频出现,不利于思维的连续、聚焦、反复.算术平方根可以先放一放,甚至被开方数、开平方也可以先放一边,只待时机成熟,一语点破.
