提高函数模型意识,凸显数学本质属性
——一道大小比较的探究
2022-10-06雷建荣
雷建荣
(甘肃省庆阳市环县第一中学,甘肃庆阳,745700)
1 问题呈现
问题(2022年广东省佛山市普通高中高三教学质量检测(二)数学试卷·12)(多选题)已知0 ( ) A. sinx C. cosx+cosy>0 D. cosx+cosy<0 此题以指数函数、三角函数为问题背景构建双参数方程,以多选题形式设置,判断三角函数值的大小关系问题.此题设置的主要目的就是考查函数的基本性质,极值点偏移等相关问题.题目难度较大,以广东省佛山市统考顺德区的11 949名学生的实际得分情况分析,平均得分1.867 3(全佛山市统考学生的平均得分为1.918),难度系数大约是38%左右. 此题的题目设计不够严密,可通过将条件进行简单变形利用不等式的性质即可求解,其次也可利用特殊值等思想选出部分选项,因而有必要进行进一步的变式与拓展.学生主要是对该题的所处的位置有一定的恐惧心理,没有深入思考,导致不必要的丢分. 方法1:(同构法1) 解析:由eysinx=exsiny,可得e-xsinx=e-ysiny. 同构函数f(t)=e-tsint,0 结合诱导公式可得e-ysiny=e-xsinx=e-xsin(π-x)>eπ-xsin(π-x),则有x 故选项C正确,选项D错误; 故选择答案:AC. 解后反思:根据题目条件的代数关系式的恒等变形,巧妙同构函数,利用函数的求导处理并确定函数的单调性,通过对应函数的单调性,并结合三角函数的基本性质综合相关的三角函数公式来分析与解决.同构函数,确定单调性,是大小比较问题中最常用的一种基本方法,关键是合理的恒等变形,巧妙同构函数,借助导数确定单调性,为进一步的应用提供条件. 方法2:(同构法2) 故选择答案:AC. 解后反思:根据题目条件的代数关系式的恒等变形,从另一层面巧妙同构函数,同样利用导数及其应用,综合函数的单调性、三角函数的图象与性质以及三角函数公式等来应用与变形,实现三角函数值大小的比较问题.不同视角的代数式的变形,对应同构的函数也是不同的,思维方式相同,技巧策略相似. 方法3:(放缩法1) 解析:因为x 由0 故选择答案:AC. 解后反思:根据不等式的基本性质,综合指数函数的图象与性质,三角函数的基本性质等进行合理的放缩变形处理,巧妙实现等量关系向不等关系的化归与转化,处理起来更加简单快捷,对数学知识与数学能力等的要求更高.等量与不等量之间的变形与转化,关键是借助函数与方程、函数的图象与性质等加以巧妙放缩与变形处理,也是解决大小比较问题中比较常用的基本技巧方法,要加以熟悉掌握. 方法4:(放缩法1) 由于0 由于0 那么cos2x-cos2y=(cosx-cosy)(cosx+cosy)>0. 结合0 故选择答案:AC. 解后反思:根据关系式的恒等变形,合理放缩,结合指数函数的单调性以及方程关系来判断两正弦函数值的大小关系,进而利用三角函数的相关公式与基本性质,通过作差比较法以及不等式的性质来进一步判断两余弦函数值的大小关系.抓住指数函数与三角函数的基本性质,合理放缩变形,是解决问题的关键,也是直击问题本质,巧妙快捷处理与分析问题的要害. 探究1:原问题设置中所给选项A和B,选项C和D均为对立状态,必有两个成立,若从特殊值等情况出发,失去压轴题的价值,进一步提升可变形为以下变式问题. 变式1(多选题)已知0 ( ) A. sinx C. cosx+cosy>0 D. sinx-cosy>0 解析:因为x 又由0 故选择答案:ACD. 解后反思:通过改变选项中的相关不等式,以不对立状态的选项内容出现,提升知识点与难度,使得问题得以进一步的升华.具体解决问题时,要更深入挖掘题目内涵与实质,剖析相关函数的基本性质,结合函数与导数的综合来分析与处理. 解决此类大小比较问题,关键就是选取合适的函数模型,深入研究函数问题,通过同构函数,借助函数的基本性质来化归;通过放缩不等式,借助函数单调性来转化等,不断积累解题经验,提高函数模型意识,借助函数的图象与性质加以数形结合,凸显数学本质属性,简捷有效处理相应的数学问题.2 问题剖析
3 问题破解
3.1 同构思维

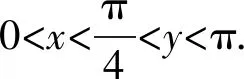
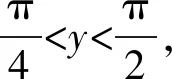
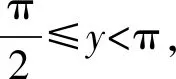

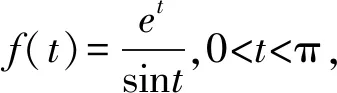

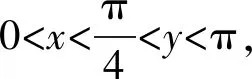
3.2 放缩思维

4 变式拓展
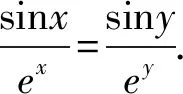
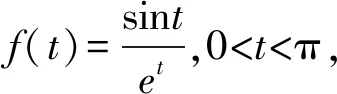

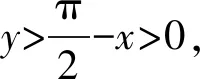
5 教学启示
