如何上好习题课
——以数轴上的动点问题习题课为例
2022-10-06张燕清
张燕清
(苏州市平江中学校,江苏苏州,215000)
习题课是在学习新课之后,教师有目的、有计划地指导学生运用已学过的知识解决一系列问题的教学活动.该课型是学生学习如何解决问题和分析问题的学习活动,就是把已经掌握的基本概念、基本的公式、法则、定理,迁移到不同的情境下组合成各类题型后,找出解决问题的方法,并探索这类问题的解题通法或内在规律.下面以一节以数轴上的动点问题习题课为例,进行说明,并提出几点建议.
1 教学分析
教材内容分析:从苏教版七年级上册的课本,我们可以看到数系刚扩充到有理数,就引出数轴的概念.数轴的重要性不言而喻.从知识层面上看,课本在讲完数轴后,利用数轴又定义了相反数、绝对值等重要概念,为后续研究有理数的运算提供了奠基作用.基于数轴的三要素,点的运动也从线段过渡到了数轴上,让数轴的应用更广泛.可见数轴是数学学习和研究的重要工具;从思想方法层面上看,数轴是数与形的结合,点在数轴上运动更是数形结合的完美体现,而数形结合思想是学生学好数学的重要思想.
教学目标:本次课是数轴的习题课,是在学生已经初步认识和理解数轴的基础上,同时也是在学完了绝对值和相反数,有理数的运算之后增设的,其目的在于进一步引导学生深化对数轴的理解,加强对数轴的应用,尤其是数轴与方程问题,行程问题的综合运用,渗透数形结合思想,建立方程的模型能力,提升数学的思维能力.
学情分析:对于刚刚升入初中的学生来说,形象思维较好,但理解能力较弱,本节内容是初学知识,学生基础不算牢固,而数轴与行程问题的综合应用,对学生的分析问题、解决问题的能力要求较高,因此对学生是一种挑战.
教学的重难点:(1) 用含有时间t的代数式表示动点的运动路程;(2) 利用数形结合的思想,判断点的运动情形,寻求等量关系,建立方程,解方程.
2 教学过程设计
数轴习题课的教学过程呈现如下:
教学环节(一) 复习引入,回顾旧知
(1) 数轴的概念,数轴的三要素.
教师要求每个学生在本子上画出一条数轴,并标出原点,正方向,单位长度.
(2) 数轴上两点间的距离怎么表示?
教师在黑板上画出一条数轴,并标出A,B两点,即引导学生得出数轴上点A,B所表示的数是a,b,则AB=|a-b| 或 |b-a|.由此总结任意两点间的距离是两点所表示的数差的绝对值.
(3) 数轴上任意两点的中点怎么表示?
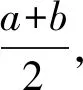
(4) 数轴上的动点如何表示?
教师画出数轴,并标出数轴上点A对应的数为-2,若点P从点A出发,以每秒4个单位长度的速度向右运动,设运动时间是t,则点P所表示的数是多少?若以每秒4个单位长度的速度向左运动,设运动的时间是t,则点P所表示的数是多少?
(5) 复习有关行程问题的典型的两种情形.
相遇问题(同时异地相向运动)
总路程=速度和×相遇时间;相遇时间=总路程/速度和;速度和=总路程/相遇时间
追及问题(同时同地同向运动)
追及时间=路程差/速度差;路程差=速度差×追及时间;速度差=路程差/追及时间
设计意图:数轴的基本概念、动点的表示方法以及行程问题的公式,是解决数轴上的动点问题的根本.通过“画图—思考—解答—概括”展现知识的形成过程,让学生从感性认识上升到理性认识,掌握概念的真正内涵,并能熟练运用,有意识地训练学生归纳概括能力.
教学环节(二) 典例呈现,引导剖析
如图,点A、点B是数轴上的点,点A表示的数是6,AB=10,动点P从点A出发,以每秒6个单位长度的速度向左匀速运动.设运动时间为t(t>0)秒.

(1) 数轴上点B表示的数是,点P表示的数是(用含t的代数式表示).
(2) 点M为AP中点,点N为BP中点,当点P在运动过程中,线段MN的长度是否发生变化?如变化,说明理由;若不变,画出图形,并求出MN的长度.
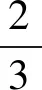
(4) 动点Q从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,动点R从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,求点Q、点R相遇时点的坐标.
(5) 动点Q从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,动点R从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,P、Q、R三个动点同时出发,点P追上点R后立即返回向点Q运动,遇到点Q则停止运动.那么点P从开始运动到停止运动,行驶的路程是多少个单位长度?
教学示范:第一问点B为定点,点P为动点,请学生自行作答,以此巩固数轴上点的表示法.点B表示的数是-4,点P表示的数是6-6t.
第二问,数轴上的任意两点的中点如何表示?点M为AP中点,点N为BP中点,
如何表示出点M,N?又如何表示M,N,两点间的距离,即是线段MN的长度?
在教师的引导下,请学生一一做答,并得出结论,不论动点P怎样运动,线段MN的长度不变,都是5.
第三问,教师引导学生发现点P,点Q的运动是什么情形?能不能在数轴上画出来?
学生1:是相遇问题.
继续引导学生,总路程和各自的速度已知,显然时间可以求出,并让每个学生自行作答.
最后相遇时点的坐标与什么相关呢?
学生2:与点P,点Q的运动路程相关.
进一步引导学生得出答案,点的坐标是2.
第四问,教师引导学生发现点P,点Q的运动问题是追及问题,路程差和各自的速度已知,显然时间可以求出.类比第三问,求出答案,点的坐标是-9.
第五问,从两个动点的运动增加到三个动点的运动,难度加大,教师引导学生画出数轴,在数轴上分析点P、Q、R三点的运动过程,分为两步.
第一步,不考虑点Q,点P与点R的运动过程是什么情形?
学生4:追及的过程.
继续引导学生得出sP=|AB|+sR,建立方程求出时间,并求出点P此时的路程s1.
第二步,不考虑点R,此时点P与点Q是相遇的过程,那么它们的路程关系是怎样的?
学生5:sP+sQ=2s1.

设计意图:此题是一道以数轴为背景来研究点的运动情形的题,综合性强,把点的运动情形考查得全面深刻.首先复习数轴上不动点和动点的表示法,并探讨点在运动过程中,线段的长度的变化规律;点的运动过程实则是行程问题,强化学生对相遇问题和追及问题的理解,并能正确分析各个点之间的路程、时间的关系,从而根据相遇和追及问题的公式建立方程.解决问题的过程是对第一环节中所学知识点的巩固和运用,渗透对学生数形结合思想和方程思想的培养,提升学生处理综合题的分析能力与解决问题的能力.
教学环节(三) 变式训练,巩固提升
1. 如图,已知A,B分别为数轴上两点,A点对应的数为-20,B点对应的数为100.

(1) 求AB中点M对应的数;
(2) 有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,求C点对应的数;
(3) 若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的D点相遇,求D点对应的数.
【预设答案】(1)M对应的数40;(2)C对应的数28;(3)D对应的数-260.
2. 动点A从原点出发向数轴负方向匀速运动,同时,动点B也从原点出发向数轴正方向匀速运动,已知动点A、B运动的速度比是1∶4,(速度单位:单位长度/秒)3秒后,两动点相距15个单位长度.
(1) 求动点A、B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
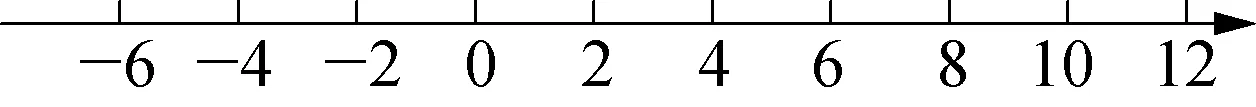
(2) 若动点A、B从(1)中的位置按原速度同时向数轴负方向匀速运动,几秒后原点恰好处在两个动点正中间?
(3)A、B两动点在(2)中的位置,继续同时向数轴负方向匀速运动时,另一动点C同时从点B位置出发向点A运动,当遇到点A后,立即返向点B运动,遇到点B后立即返向点A运动,如此往返,直至点B追上点A时,点C立即停止运动,若点C一直以20单位长度/秒的速度作匀速运动,那么,点C从开始到停止运动,其运动的路程是多少单位长度?

设计意图:第一题是以电子蚂蚁为背景设计的,考查动点的相遇和追及问题,是对例题的进一步巩固深化.第二题三问与例题相比存在差别的,但仍是对行程问题结合数轴知识的活用,第一问是背向而行,较简单,第二问同向而行,由于原点恰好处在两个动点正中间,即用坐标表示出动点,得到两点坐标的和为0即可解决问题.第三问是点A、B的追及问题,点C的折返问题,在变化中寻求相等的量即是三动点的运动时间相等,由此解决问题.两道例题是对所学知识的巩固,深化与拓展,加深学生对知识的理解和运用.
3 关于习题课的几点建议
3.1 习题课需要梳理回顾相关知识点
习题课的第一教学环节是需要梳理相关概念、性质等知识,为后面的解题做铺垫.如上面数轴的习题课开课时,教师带学生把与数轴相关的一些概念、性质、点的行程问题都梳理了一遍,促进学生自主建构、 形成知识网络、完善知识体系.
3.2 习题课需要精心设计题目
一节习题课质量的高低很大程度上取决于教师对习题的选择.教师在习题的编选上要下足功夫,要选择典型的、有代表性的例题,让例题体现主要知识点的运用、体现通解通法,能起到加强双基的示范性;要选择一些关联性强的习题,可以是同一个知识点的深化与巩固,也可以是一个知识点与其他知识在不同背景下的组合运用;要精心配置习题的难易程度,既有重基础的简单题型,也有变式拓展类题型,提高型、创新型等难度较大的题型,让学生在抓基础的同时,提高分析和解决较为复杂的具有灵活性和综合性问题的能力,发展数学思维.如上面的例题,是经过改编的,除了对所复习的知识点的运用,以此巩固双基,也是对同一知识(相遇与追及问题)的不断深化应用,在难易程度上也是逐步提升,以满足各个层次的学生.
3.3 习题课教学方式要多样化
习题课教学知识密度大、题型多,如果只是依靠教师一味地讲授,会让学生感到枯燥、乏味,丧失学习的积极性.在习题课中教师始终把握以教师为主导,学生为主体的原则,组织多样化的教学方式.如采用设置问题串的形式,将一些看似复杂的综合的问题分解成较为精细的几个小问题,教师有效引导学生根据所学过的知识先解决“小问题”,再突破“大问题”.如分组讨论的方式让学生多动口、多动手、多动脑,激发学生全方位“参与”问题的解决,有效地减轻学生的“疲劳”,提高课堂教学的效率和质量.
